基于有限元技术的数控专用磨床砂轮主轴静态性能研究

丘永亮，王 平

（广东工贸职业技术学院机械工程系，广东广州 510510）

0 引言

随着我国高等级公路的迅速发展，全社会汽车保有量接近三千万辆，子午线轮胎的需求大幅度增加，子午线轮胎模具特别是活络模具的发展速度远远高于模具平均水平，目前，子午线轮胎在世界范围已是轮胎工业的主流产品，世界轮胎子午化率达90%，发达国家已达到或接近100%。子午线轮胎以其耐磨、高速、舒适、节油的特点受到人们的广泛重视。制造子午线轮胎使用的模具是子午线活络模具，曲面成型轮胎侧板是子午线轮胎模具的主要组成零件，其精度对轮胎制品性能有决定性影响。国外子午线轮胎模侧板曲面加工工艺方法是不公开的，但从产品分析应该是通过机械精密加工完成的。为了实现子午线轮胎模侧板曲面的砂轮轨迹包络磨削加工过程，需要设计和研制一种具有轴对称曲面的子午线轮胎活络模具轮胎侧板成型曲面专用数控磨床。

对于该专用数控磨床，砂轮主轴是其关键零件，其结构的合理性和强度将直接影响数控磨床的加工效率和精度，液体静压轴承具有摩擦阻力和功率消耗小，传动效率高，精度保持性好和速度变化对油膜刚度影响小等优点，广泛用于精密机床结构中。

有限元作为结构分析和辅助设计的常用技术，其基本思想是将连续的求解区域离散成有限个、且按一定方式相互联结在一起的单元组合体。然后，利用每一个单元体内假设的近似函数来分片表示求解域上待求的未知场函数[1-2]。ANSYS 是一款应用非常广泛的有限元分析软件，主要应用于结构、热、流体、电磁、声学等领域。

在数控专用磨床设计研制中，利用有限元技术对砂轮主轴进行静态性能分析，可大大提高其设计的效率和精度。

1 砂轮主轴结构及受力分析

1.1 砂轮主轴结构

在专用数控磨床中，砂轮主轴运转必须具有良好的回转精度、平稳性和吸振性，参照目前砂轮主轴设计的主体方向，砂轮主轴的轴承采用液体静压轴承。液体静压轴承主要靠外部供给压力油，在轴承内产生静压承载油膜以实现液体润滑的滑动轴承，砂轮主轴结构如图1所示。

图1 砂轮主轴的结构

1.2 砂轮主轴受力分析

（1）液体静压主轴的材料与基本结构

在专用数控磨床中，根据砂轮主轴的工作状况，其材料选择40Cr合金结构钢，调质处理。砂轮主轴的两端一般分别装工作机构、电机等，考虑安装与密封，其结构为阶梯形状，如图1所示。

（2）砂轮主轴的受力分析

在专用数控磨床中，砂轮主轴的受力主要有：①主轴零件的重量，作用在主轴的中间；②与驱动电机相接的联轴器的重量，悬挂在主轴的一端；③工作机部分的重量，悬挂在主轴的另一端；④主轴在工作时，受到工件的反作用力；⑤主轴在电动机的驱动下作旋转运动所产生的扭矩等。因此砂轮主轴属于受弯曲和扭转组合变形的转轴，砂轮主轴各液压轴承支承处的受力简图如图2（a）所示，各部分弯矩如图2（b）所示，各部分扭矩如图2（c）所示。

（3）油膜刚度的确定

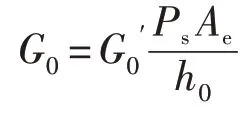
油膜刚度与轴承有效承载面积（Ae）、润滑油特性、供油压力（Ps）、轴承半径间隙等有关。

在专用数控磨床中的砂轮主轴的结构设计中[3-4]，其液体静压轴承用油选用AN32 号，该用油在50度时的动力黏度和运动 黏 度 分 别 为:η50=193，γ50=0.22 ； 当节流比（β）为0.5 时，轴承具有最佳的刚度；在满足轴承最大承载能力和足够刚度条件下，供油装置功率消耗最小的原则，其供油压力（ps≥98）选择为147；根据设计中的配合关系H7/h6，其公差为0.041 mm，轴承半径间隙约为0.02 mm。

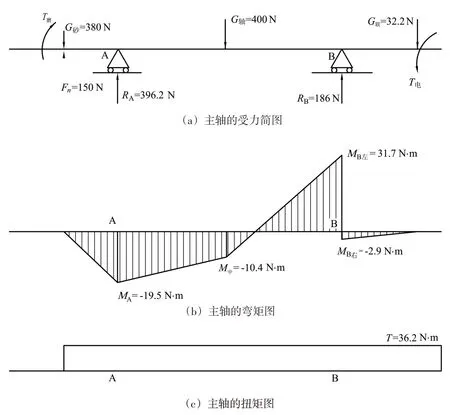
图2 砂轮主轴受力图

当专用数控磨床中的液体静压轴承直径为50 mm（L/D=1）时，则油腔宽度（l）为40 mm，轴向封油面宽度（l1）为5 mm，油腔夹角（θ）为60°，周向封油夹角（θ1）为12°，回油槽夹角（θ2）为6°，回油槽深度为0.6 mm，周向封油面宽度（D sin（θ1/2））为0.525 mm，回油槽宽度（D sin（θ2/2））为0.258 5 mm，油腔有效夹角（θm=（θ1+θ2）/2）为36°。

轴承有效承载面积:

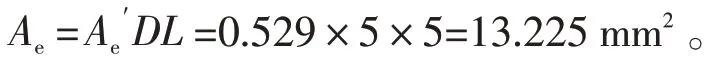
根据机械设计手册[5]有：

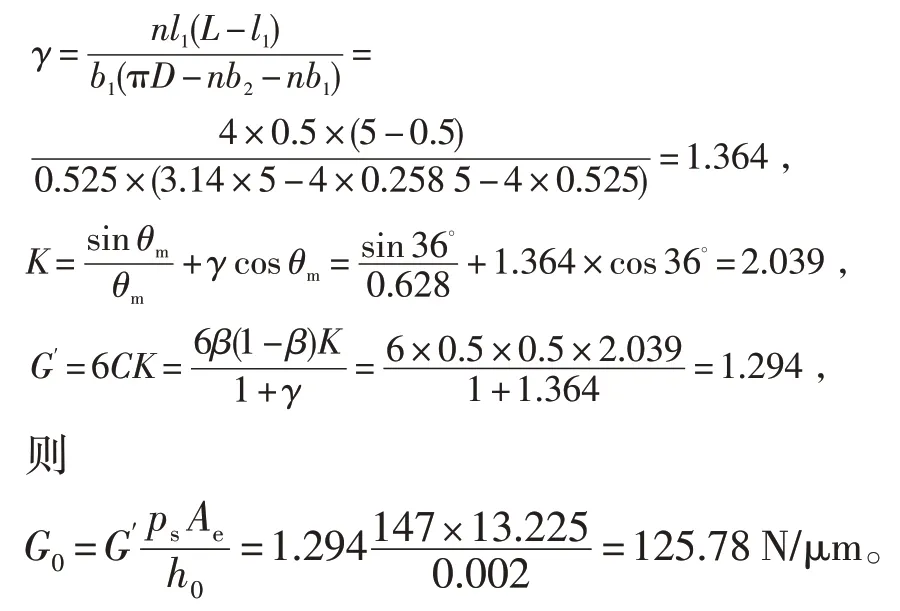
以上计算式子中，D为轴承直径，L为轴承宽度，Ae为轴承承载面积，G0为油膜刚度，ps为供油压力，β 为节流比，l1为轴向封油面宽度，K 为载荷分布系数。

2 砂轮主轴静态性能有限元分析

2.1 砂轮主轴有限元模型的建立

在整个砂轮主轴支撑与传动系统中，主轴主要承担径向载荷，所以，利用两个液体静压轴承来承受径向载荷。略去径向轴承因加载倾斜产生的转矩，这样可以把整个主轴系统进一步简化为如图3所示的弹性支承。

图3 主轴系统几何模型

在一个平面内，对单个梁单元可在水平和竖直两平面分别分析计算，单元两端的载荷分别是剪力和弯矩，产生的变形表现为挠度和转角。用垂直于轴线X 的平面内的水平和竖直方向（Y 与Z）的两根可压缩弹簧进行线性叠加来等效主轴上的液态静压轴承，支点位于主轴上对应压力最高的油腔中心位置处，弹簧的刚度特性可通过上面计算的油膜刚度得出。

2.2 用ANSYS求解砂轮主轴的静态性能

（1）单元选择。砂轮主轴可采用BEAM188单元进行网格划分，单元的几何形状、坐标系、和节点坐标如图5 所示。在全局坐标系统中该单元由节点I和J定义，节点K是定义单元方向的可选项，本主轴因为是中心对称结构不需要定义K。面①～⑤用于定义面载荷，单元的主要输入与输出参数可见表1。用ANSYS 提供的弹簧单元COMBIN39 模拟轴承，单元的主要输入与输出参数见表2。

表1 BEAM188单元的主要输入/输出参数

表2 COMBIN39单元的主要输入/输出参数

（2）模型输入及单元划分。在ANSYS中建立的“全支承”主轴有限元静态分析模型如图7 所示，主轴材料为Cr40，假定为各向同性的线弹性材料，取弹性模量EX=1.93E5MPa，泊松比PRXY=0.27，材料密度DENS=7.86E-6 kg/mm3，用BEAM188 划分主轴共可得到116 个单元、117 个节点。

图4 用ANSYS建立的主轴有限元模型

图5 主轴受载变形及位移分布图

（3）求解。有限元模型建好后，对其施加边界条件、载荷，确定求解类型并运行求解。砂轮主轴的静态性能分析结果即载荷与主轴端面位移之间的关系如图5、图6所示。

3 结论

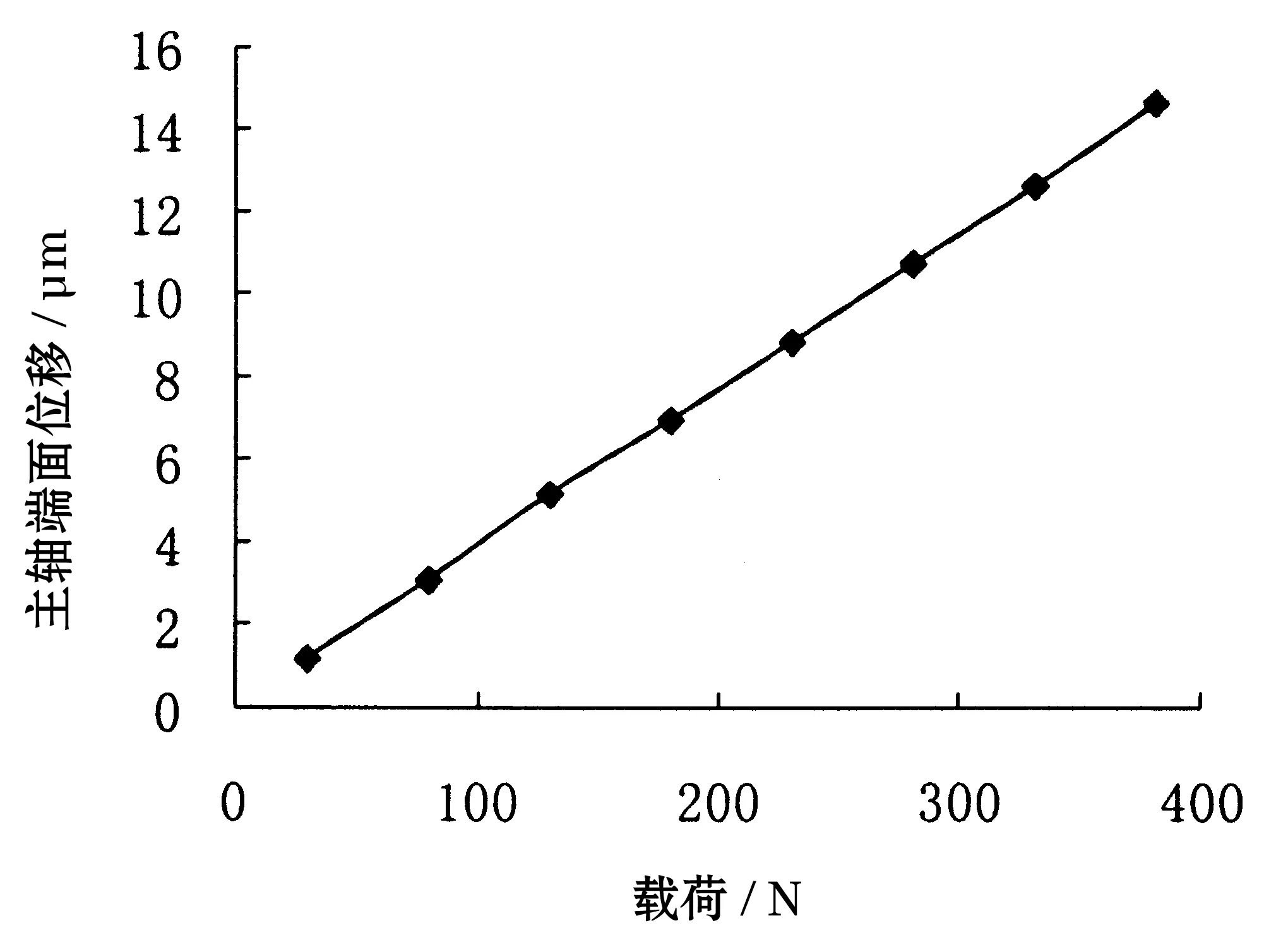
图6 载荷与主轴端面位移之间的关系

通过液体静压轴承系统中的砂轮主轴静态性能有限元分析，可得到主轴前端加载点的径向位移与载荷之间的关系，当在主轴前端施加向下（Y轴负方向）的集中力后，主轴发生倾斜，前端下沉，中间部分向上弯曲。在载荷的作用下，主轴的弯曲变形主要是因为液体静压轴承油膜受压变形引起的，主轴的抗弯刚度比轴承刚度大，弯曲变形小，这样，通过有限元技术可以较合理地确定砂轮主轴的参数。因此，有限元技术在数控专用机床设计中的应用将对提高机床设计的精度和效率起到非常重要的作用。

［1］王勖成，邵敏.有限单元法基本思想和数值方法：第2版［M］.北京：清华大学出版社，1997.

［2］孙庆，应富强.基于有限元分析的60MN挤压铸造机主液压缸设计［J］.机电工程，2011（1）：33-37.

［3］王德泉.砂轮特性与磨削加工［M］.北京：中国标准出版社，2001.

［4］陆元章.现代机械设备设计手册［M］.北京：机械工业出版社，1996.

［5］濮良贵，纪名刚.机械设计［M］..北京：高等教育出版社，2000.