Hydrodynamic modeling of cochlea and numerical simulation for cochlear traveling wave with consideration of fluid-structure interaction*

REN Liu-jie (任柳杰), HUA Cheng (华诚), DING Guang-hong (丁光宏)

Department of Mechanics and Engineering Science, Fudan University, Shanghai 200433, China,

E-mail: 10110290005@fudan.edu.cn

YANG Lin (杨琳), DAI Pei-dong (戴培东), ZHANG Tian-yu (张天宇)

Research Center, Eye and ENT Hospital of Fudan University, Shanghai 200031, China

Hydrodynamic modeling of cochlea and numerical simulation for cochlear traveling wave with consideration of fluid-structure interaction*

REN Liu-jie (任柳杰), HUA Cheng (华诚), DING Guang-hong (丁光宏)

Department of Mechanics and Engineering Science, Fudan University, Shanghai 200433, China,

E-mail: 10110290005@fudan.edu.cn

YANG Lin (杨琳), DAI Pei-dong (戴培东), ZHANG Tian-yu (张天宇)

Research Center, Eye and ENT Hospital of Fudan University, Shanghai 200031, China

(Received December 17, 2011, Revised March 15, 2013)

The cochlea is an important structure in the hearing system of humanity. Its unique structure enables the sensibility to the sound waves of varied frequencies. The widely accepted model of the cochlea is expressed as a long tube longitudinally divided by a membrane named the Basilar Membrane (BM), into two fluid-filled channels. Based on various assumptions for the cochlear fluid and structure, simplified mathematical and mechanical cochlear models were developed to help to understand the mechanism of the complex coupled system in the past decades. This paper proposes a hydrodynamic numerical cochlear model with consideration of the Fluid-Structure Interaction (FSI). In this model, the cochlear lymph is considered as in a Newtonian viscous fluid, and the basilar membrane is modeled as a composite structure. The traveling wave is simulated. Also focusing on the pressure in the fluid field, the results are compared with studies of Peterson and Bogert, where it was assumed that the slow compressive waves are traveling along the BM. Furthermore, the transmitting time of the cochlear traveling wave is also discussed.

cochlea, traveling wave, finite-element method, Fluid Structure Interaction (FSI)

Introduction

The cochlea, the auditory transducer and sensor, is an essential part of the human hearing system. As shown in Fig.1(a), the sound waves are usually conducted sequentially through the external acoustic meatus, the tympanic membrane, the ossicular chain in the middle ear, to the cochlea in the inner ear (called the air conduction). The human cochlea is a spiral-shaped cavity in the bony labyrinth, making 2.5-2.75 turns around the osseous spiral lamina. In a local view of the cochlea, as shown in Fig.1(b), the snail-shell like structure is divided longitudinally by two membranes into three channels filled with the lymph, a watery fluid. Two of the channels named the scala vestibula and the scala tympani are connected at the helicotrema. At the basal end of the cochlea in the scala vestibula is the oval window, a membrane-covered opening directly contacted by the stapes in the middle ear; and in the scala tympani is the round window. The third channel, the scala media, is a close and relatively small duct filled with the endolymph and contains the organ of corti, which is the sensory organ of hearing.

Figure 1(c) is a usual 2-D mechanical model of the cochlea. Although the coiling of the cochleae affects the cochlear response, especially, in the low frequency range[1], the cochlea here is unwrapped, for the traveling wave features are similar; and the scala media is merged with the scala vestibula for the Reissner’s membrane is thin and soft so that it moves simultaneously with the surrounding fluid. The sound waves are transmitted to the oval window of the cochlea to create a pressure difference between the scala vestibula and the scala tympani, thus displacing the Basilar Membrane (BM), which separates the two scalae, in the transverse direction. Along the BM,

Fig.1 Human cochlea

Traveling Waves (TW) propagate from the basal end towards the apical end. This important phenomenon was first confirmed in the pioneer experiments conducted by Von Békésy[2]. It is also observed that the TW amplitude reaches a peak at a small region (which is called the characteristic frequency location or the CF location). The CF location depends broadly on the sound frequency: high frequencies lead to the maximum vibrations near the basal end of BM, where the membrane is narrow and stiff, while low frequencies lead to the maximum vibrations near the apical end, where the membrane is wider and more compliant.

Studies of the cochlear modeling and numerical simulations related to the traveling waves were carried out over the past decades. Many mechanical and mathematical cochlear models of various dimensions were proposed. Since the Fluid-Structure Interaction (FSI) features the cochlear dynamics, the cochlear modeling should involve the modeling of the fluid domain (lymph), the structure domain (mainly the BM, or the partition) and the interaction between them. For the modeling of the BM, in some models (usually in 1-D and 2-D models), the BM is considered to be a series of locally reacting structures, of which the mechanical behavior is expressed by the impedance function[3-8], while in other models (mostly seen in 3-D models), the BM is modeled as an orthogonal plate controlled by laws of elasticity[9-12]. For the fluid domain, the lymph is modeled as an invicid potential flow[3,13]or a Newtonian viscous flow[12,14]governed by corresponding governing equations. Various methods were used to solve these cochlear models, such as the finite difference[3], the finite element[12,13], the WKB method[7-10], and the immersed boundary method[14].

In this paper, a new cochlear hydrodynamic model with consideration of the FSI is developed to simulate the TW phenomenon, one of the most notable features of the cochlear dynamic behaviors. Based on our simulation results, the vibration patterns of the BM and the pressure properties of the cochlear lymph at different sound input frequencies are discussed, and compared with experimental observations or previous studies. Furthermore, this study also explores the transmitting time of cochlear traveling waves.

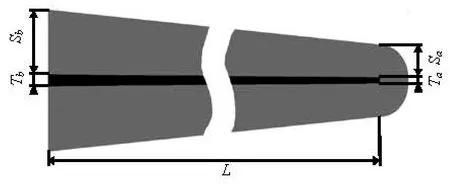
Fig.2 Schematic diagram of the 2-D cochlear model

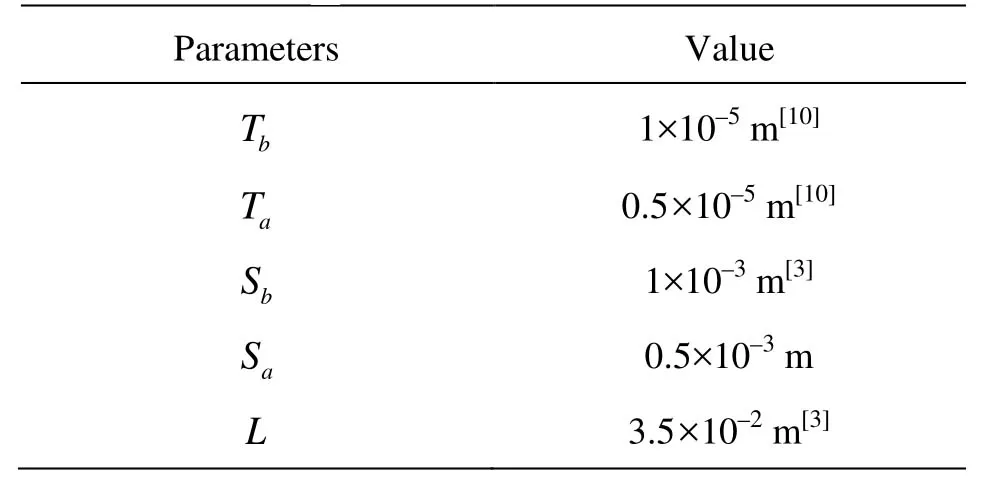
Table 1 Geometric parameters

1. Method

The 2-D cochlear model is considered. The duct height varies linearly from the base to the apex (see Fig.2, the geometric parameters are listed in Table 1). The cochlear fluid is modeled as the incompressible viscous flow. The body forces are neglected, but the nonlinear convection terms in the Navier-Stokes equation are retained. Thus, the governing equations for the fluid are

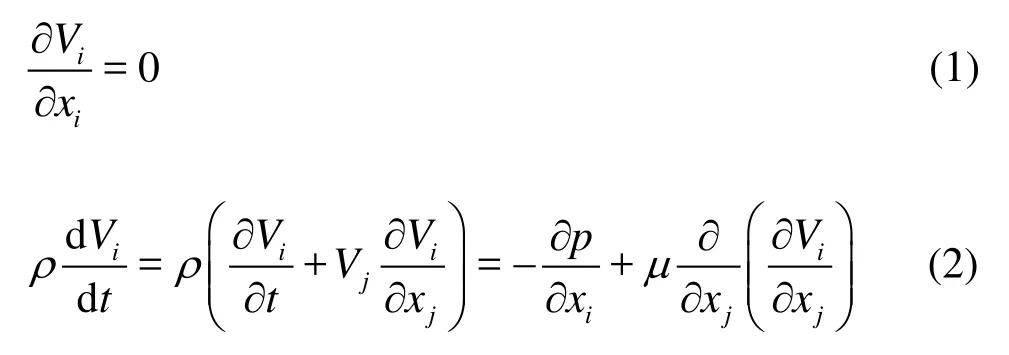
where Viand p are, respectively, the fluid velocity in the vector form and the fluid pressure, which are the basic unknowns of the PDEs,µandρare, respectively, the dynamic viscosity and the density of the fluid: these two parameters are close to those of water (see Table 2 for a list). Non-slip conditions are assumed for all the fluid boundaries.

Table 2 Fluid properties

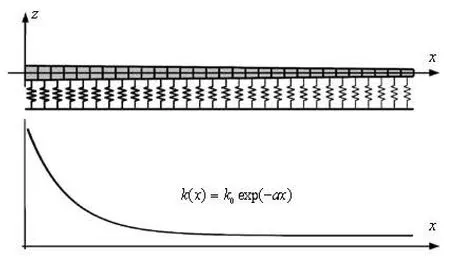
Fig.3 Schematic diagram of the BM model. Springs with varying properties are attached to the BM segments of length Δx

The entire BM model is illustrated inFig.3. The model has two components. The first component is the spring-damper structures attached to the BM, with varying properties in the longitudinal direction(x). This component models the stiffness variation of the BM from the base to the apex. The corresponding dynamic equation is

where m is the mass of the BM per unit length,c andk are the damping coefficient and the stiffness of the springs, respectively, per unit length,ζis the transverse displacement of the BM, andP is the driving force contributed by the fluid domain. As previous cochlear models suggest, approximately, the stiffness k( x)decreases exponentially longitudinally, and the mathematical description of k( x)is

where k0anda are constants.

The second component is a 2-D plane-strain model of the BM, which models the longitudinal coupling of the BM. The equilibrium equation, the constitutive relation, and the geometric relation for the elastic BM are

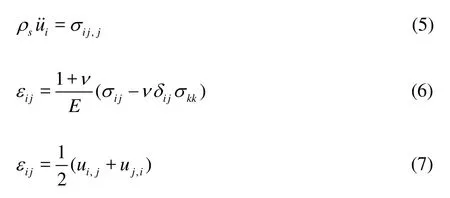
where ρs,E andνare the density, the Young’s modulus, and the Poisson’s ratio of the BM, respectively. All material properties for the BM and the springs are listed in Table 3.

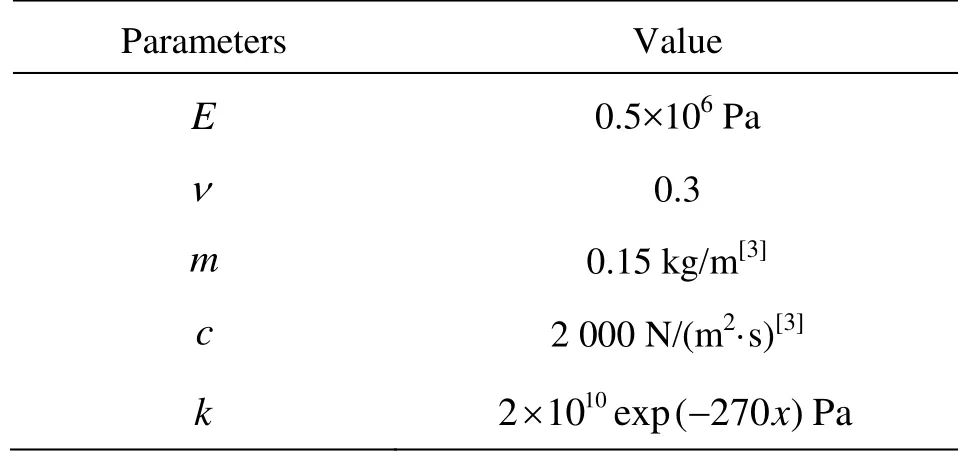
Table 3 Material properties of the BM structure

In the FSI, the Lagrangian coordinate system is used for the BM and the Arbitrary-Lagrangian-Eulerian (ALE) coordinate system is used for the fluid. The primary variable for the BM is the displacements, and the primary variables for the fluid are the fluid pressure, the velocity, and the displacement. Denote X =(Xf, Xs)as the solution vector of the coupled system, where Xfand Xsare the variable vectors for the fluid and the BM, respectively. The coupled system can be written as

where Ffand Fsare, respectively, the fluid and BM equations corresponding to Eqs.(1)-(2) and Eqs.(3), (5)-(7),usand τfare the BM displacement and the fluid stress, respectively, defined on the fluid-BM interface only. Eq.(8) shows that the BM displacementsmodify the fluid domain (as in the us(Xs)term), and the fluid applies the force on the BM (as in the τf(Xf)term). The nonlinear system is solved iteratively. The convergence criteria for the stress and displacements are

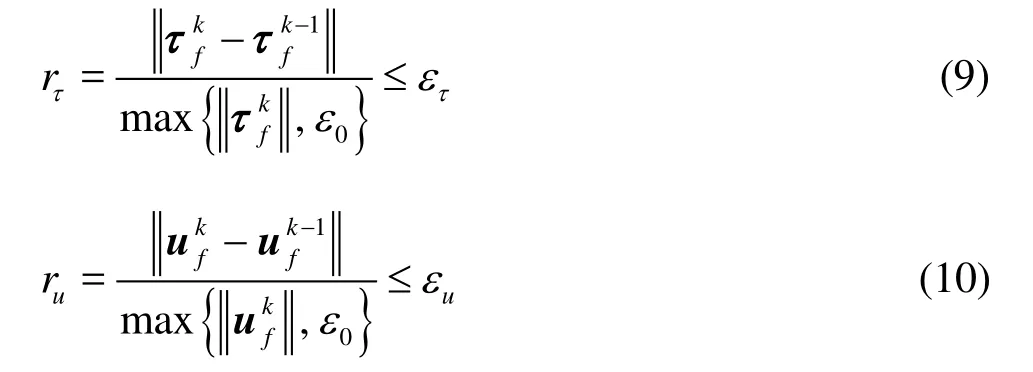
where the superscript k denotes the index of the step in the iteration,ετand εuare the tolerances for the stress and the displacement, respectively,ε0is a predetermined constant (10–8).

The system is solved numer©ically through the finite element package ADINA. As shown in Fig.4(a), the BM is modeled by 2 000 4-node solid elements. The black dots in the figure are the places where the springs are attached. The fluid domain is also modeled by 4-node 2-D elements (see Fig.4(b)). The entire model contains 32 310 elements and 33 343 nodes.

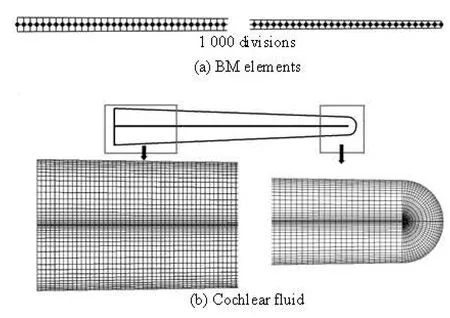
Fig.4 Finite element model

2. Simulation results and analyses

In this section, the simulation results are presented and some cochlear dynamic problems are discussed. For these simulations, a sinusoidal time-dependent velocity,Vs, of various frequencies, is applied on the oval window (x =0,Tb/2＜y＜Sb) in the form of

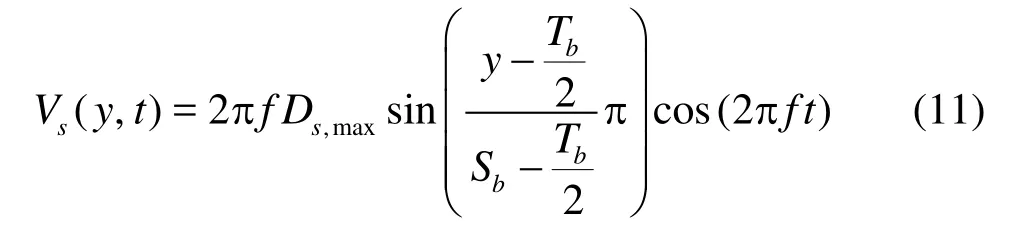
where Dsrepresents the displacement amplitude of the oval window, and f is the exciting frequency, Ds,maxis assumed to beµm, so that the average amplitude of the oval window,Ds,avgis equal to 1 µm. Five different cases, with the exciting frequency ranging from 250 Hz to 4 000 Hz, are simulated, under the simulation conditions as listed in Table 4.

Table 4 Simulation conditions

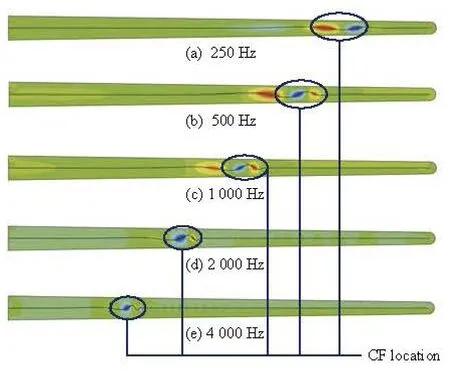
Fig.5 A sketch for the simulation results. The contour represents the fluid velocity in vertical direction

Fig.6 Partial enlarged view of the deformations of the fluid and solid elements

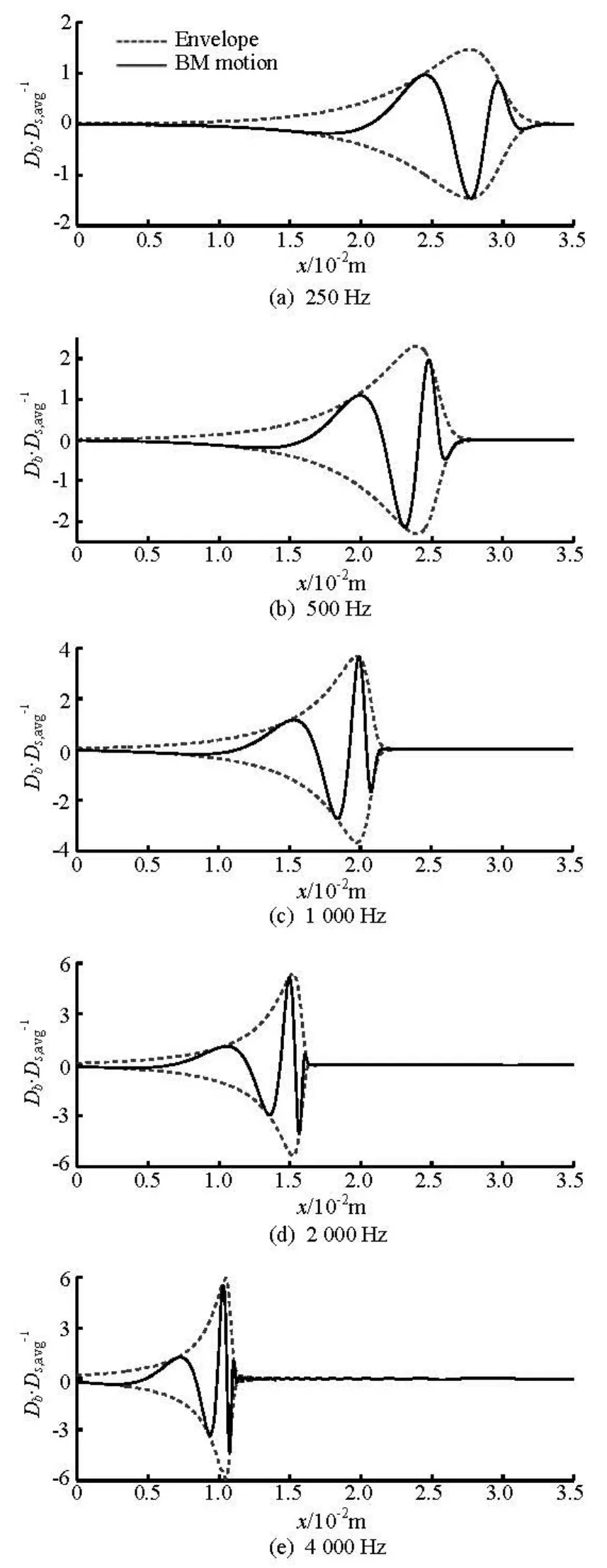
Fig.7 BM vibration patterns at different frequencies

The cochlear dynamic response is simulated phenomenally. The CF location differs according to the exciting frequency, as shown in Fig.5, in which the deformation of the model is magnified by 50-100 times for a clear view of the BM’s movement. Partial enlarged details (2 000 times) of the deformation of elements near the CF location are given in Fig.6, where the fluid and the solid elements converge together while moving. The z -directional displacement of the BM is obtained and the vibration patterns are shown as in solid lines in Fig.7, where the dash lines are the vibration envelopes. The BM displacement is normalized by the stapes displacement,Ds,avg. The simulation results are in qualitative agreement with the traveling wave theory: for high frequency sounds, the BM vibration peak is closer to the stapes, and as the frequency decreases, the wave peak moves towards the apical end.

Fig.8 Pressure properties

There are two different pressures in the scala vestibula (PSV)and in the scala tympani (PST). Figure 8 gives this two pressure distribution along the scalae when the stapes moves inwards. The pressures are normalized by the pressure at the oval window. It is universally agreed that the intracochlear pressure is closely interacted with the BM motion. The difference (Pd= PSV-PST)between the two pressures causes the BM to deflect, that is, the vibration of the BM. The simulation results show that the magnitude ofPdis large at the base of cochlea and it decreases as it goes far from the stapes. Where the pressure difference vanishes, that is,PSVis equal to PST, the BM motion dies away.

Fig.9 TW transmitting process

Another important feature of the cochlear traveling wave is the transmitting time, which can be defined as the required time for a single wave traveling from the basal end of the BM to the CF location. The transmitting time is an essential feature of cochlear dynamical behaviors because it is an important part of the delay time for human to perceive sounds. So far there is no available way to directly measure the transmitting time in the human cochlea. In this simulation, the transmitting time of the cochlear traveling wave can be calculated by tracing the propagation process of a single wave peak (see Fig.9). At timet0, the stapes moves outward, thus a traveling wave peak forms and it travels in the direction of the apical, and till timetswhen the wave peak reaches the CF location. The time duration,ts-t0, is regarded as the transmitting time, and is listed in Table 5 for different frequencies. It is obvious that the higher the frequency is applied, the shorter the transmitting time is. This is due to two facts: (1) the CF location of a higher frequency is closer to the stapes and (2) the TW travels faster when it is closer to the stapes.

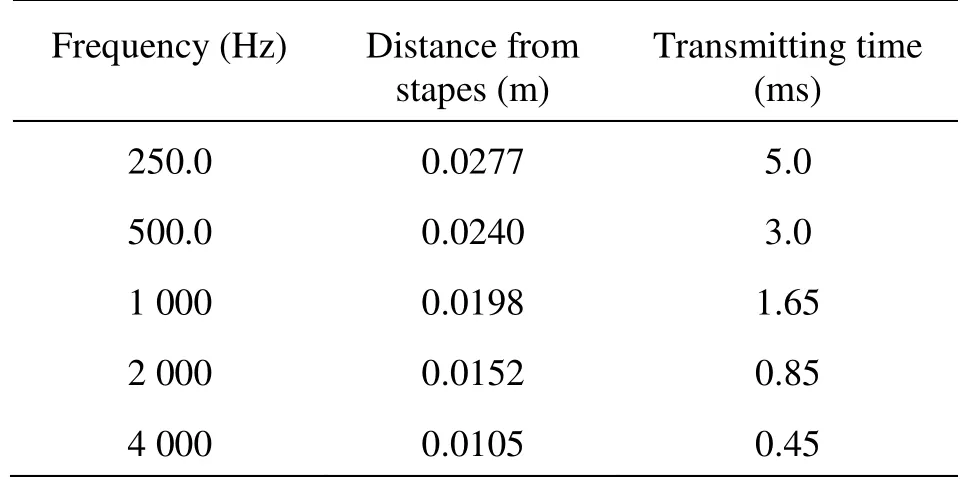
Table 5 Frequencies, CF locations and transmitting times

Several indirect ways were developed to measure the time and the velocity properties of the traveling wave. Zerlin[15], Kimberley[16]analyzed the traveling velocity of the cochlear travelling wave. Strelcyk and Dau[17]re-conducted Zerlin’s experiments and the same phenomena were duplicated. Moreover, the Auditory Brainstem Responses (ABRs) were measured. The ABR results also show that human response time to the sounds increases with lowering of frequencies.

3. Conclusions

A new hydrodynamic cochlear model is proposed in this paper with consideration of the FSI between the BM and the cochlear lymph. The following conclusions are drawn:

(1) The model simulates the phenomena of the cochlear traveling wave phenomena, first observed by Von Békésy. It is confirmed by the simulation that sounds of high frequencies cause the maximum vibration near the basal end of the BM, and sounds of low frequencies cause the maximum vibration near the apical end of the BM.

(2) The pressure difference along the BM vanishes when the BM’s amplitude reaches the maximum. The result is in good agreement with the theoretical analysis by Peterson and Bogert.

(3) The transmitting time of the traveling wave to reach the CF location varies with the frequency. Lower frequencies lead to longer time.

This model is a very simplified cochlear model, and more complicated features such as the 3-D spiral structure and the nonlinear effects should be considered in further studies of cochlear dynamics.

Acnowledgement

We are very grateful to Professor Steele C. R. (Stanford University) and to one of anonymous reviewers for their helpful suggestions and detailed corrections regarding the original manuscript.

[1] MANOUSSAKI D. CHADWICK R. S. and KETTEN D. R. et al. The influence of cochlear shape on low-frequency hearing[J]. Proceedings of the National Academy of Sciences of the United States of America, 2008, 105(16): 6162-6166.

[2] Von BÉKÉSY G. Experiments in hearing[M]. New York, USA: McGraw-Hill, 1960.

[3] NEELY S. T. Finite difference solution of a two-dimensional mathematical model of the cochlea[J]. Journal of the Acoustical Society of America, 1981, 69(5): 1386-1393.

[4] PETERSON L. C., BOGERT B. P. A dynamical theory of the cochlea[J]. Journal of the Acoustical Society of America, 1950, 22(3): 369-381.

[5] LÜLING H., FRANOSCH J. M. and Van HEMMEN J. L. A two-dimensional cochlear fluid model based on conformal mapping[J]. Journal of the Acoustical Society of America, 2010, 128(6): 3577-3584.

[6] VETEŠNÍK A., NOBILI R. The approximate scaling law of the cochlea box model[J]. Hearing Research, 2006, 222(1-2): 43-53.

[7] STEELE C. R. Comparison of WKB and Finite difference calculations for a two-dimensional Cochlear model[J]. Journal of the Acoustical Society of America, 1979, 65(4): 1001-1006.

[8] STEELE C. R., TABER L. A. Comparison of WKB calculations and experimental results for three-dimensional cochlear models[J]. Journal of the Acoustical Society of America, 1979, 65(4): 1007-1018.

[9] LIM K.-M., STEELE C. R. A Three-dimensional nonlinear active Cochlear model analyzed by the WKB-numeric method[J]. Hearing Research, 2002, 170(1-2): 190-205.

[10] LIM K.-M., STEELE C. R. Response suppression and transient behavior in a nonlinear active cochlear model with feed-forward[J]. International Journal of Solids and Structure, 2003, 40(1): 5097-5107.

[11] BÖHNKE F., ARNOLD W. 3D-finite element model of the human cochlea including fluid-structure couplings[J]. Journal for Oto-Rhino-Laryngology, Head and Neck Surgery, 1999, 61(5): 305-310.

[12] CHENG L., WHITE R. D. and GROSH K. Three-dimensional viscous finite element formulation for acoustic fluid-structure interaction[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(49-50): 4160-4172.

[13] PARTHASARATHI A. A., GROSH K. and NUTTAL A. L. Three-dimensional numerical modeling for global cochlear dynamics[J]. Journal of the Acoustical Society of America, 2000, 107(1): 474-485.

[14] GIVELBERG E., BUNN J. A comprehensive three-dimensional model of the cochlea[J]. Journal of Computational Physics, 2003, 191(2): 377-391.

[15] ZERLIN S. Travelin wave velocity in the human cochlea[J]. Journal of the Acoustical Society of America, 1969, 46(4B): 1011-1015.

[16] KIMBERLEY B. P. Measuring human cochlear traveling wave delay using distortion product emission phase responses[J]. Journal of the Acoustical Society of America, 1993, 94(3): 1343-1350.

[17] STRELCYK O., DAU T. Estimaion of cochlear response times using lateralization of frequency-mismatched tones[J]. Journal of the Acoustical Society of America, 2009, 126(3): 1302-1311.

10.1016/S1001-6058(13)60351-0

* Project supported by the Shanghai Committee of Science and Technology of China (Grant No. 10ZR1403500, 10ZR1405800), the National Basic Research Development Program of China (973 Program, Grant No. 2012CB518502) and the National Natural Science Foundation of China (Grant No. 30971528).

Biography: REN Liu-jie (1987- ), Male, Ph. D. Candidate

HUA Cheng,

E-mail:huacheng@fudan.edu.cn