Parametric instability of a liquid metal sessile drop under the action of low-frequency alternating magnetic fields*

LEI Zuo-sheng (雷作胜)

Shanghai Key Laboratory of Modern Metallurgy and Materials Processing, Shanghai University, Shanghai 200072, China

SIMAP-EPM Laboratory, Grenoble Institute of Technology/CNRS UMR 5266, France

E-mail:lei_zsh@staff.shu.edu.cn

GUO Jia-hong (郭加宏)

Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China

FAUTRELLE Yves, ERNST Roland, ETAY Jacqueline

SIMAP-EPM Laboratory, Grenoble Institute of Technology/CNRS UMR 5266, France

REN Zhong-ming (任忠鸣)

Shanghai Key Laboratory of Modern Metallurgy and Materials Processing, Shanghai University, Shanghai 200072, China

Parametric instability of a liquid metal sessile drop under the action of low-frequency alternating magnetic fields*

LEI Zuo-sheng (雷作胜)

Shanghai Key Laboratory of Modern Metallurgy and Materials Processing, Shanghai University, Shanghai 200072, China

SIMAP-EPM Laboratory, Grenoble Institute of Technology/CNRS UMR 5266, France

E-mail:lei_zsh@staff.shu.edu.cn

GUO Jia-hong (郭加宏)

Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China

FAUTRELLE Yves, ERNST Roland, ETAY Jacqueline

SIMAP-EPM Laboratory, Grenoble Institute of Technology/CNRS UMR 5266, France

REN Zhong-ming (任忠鸣)

Shanghai Key Laboratory of Modern Metallurgy and Materials Processing, Shanghai University, Shanghai 200072, China

(Received November 23, 2012, Revised February 27, 2013)

A 2-D mathematical model is developed in order to simulate a parametric electromagnetic instability oscillation process of a liquid metal droplet under the action of low frequency magnetic field. The Arbitrary Lagrangian-Eulerian (ALE) method and weak form constraint boundary condition are introduced in this model for implementation of the surface tension and electromagnetic force on liquid droplet free surface. The results of the numerical calculations indicate the appearance of various regimes of oscillation. It is found that according to the magnetic field frequency various types of oscillation modes may be found. The oscillation is originated from an instability phenomenon. The stability diagram of liquid metal droplet in the parameter space of magnetic frequency and magnetic flux density is determined numerically. The diagram is very similar to that found in the so-called parametric instability.

sessile drop, parametric instability, low-frequency alternating magnetic fields, numerical simulation

Introduction

Alternating magnetic fields, including low-, medium- and high-frequency magnetic fields, are usually imposed on liquid metal pool or drops in order to control both internal flow field and free surface behavior. This is a problem of great scientific and technological interest in many processes[1], such as cold crucible[2], electromagnetic levitation[3], welding[4]and electron beam evaporation[5]. In metallurgy and liquid metal refining processes low frequency magnetic field may be used to create free surface agitation which promotes mass transfers in through the interface between the liquid metal and the covering slag or molten salt[1].

In these applications, electromagnetic force due to interaction between imposing magnetic field and induced electrical currents may cause considerable free surface deformation. It has been observed by Fautrelle et al.[6]that the periphery of the free surface behavior of a thin pool of mercury is determined by the magnetic field amplitude and frequency when it is subjected to a vertical low-frequency magnetic field. They found various regular and irregular free surface patterns among which a structured wave is excited with relatively large magnetic field amplitude. This kind of wave with appearances of polygonal plane shape is considered to be a parametric-type instability caused by the alternating electromagnetic force.

As an extension of the previous investigation, the present work develops a 2-D mathematical model based on the finite element method able to simulate the parametric instability behavior of liquid metal droplet under a vertical low-frequency magnetic field. This model uses the Arbitrary Lagrangian-Eulerian (ALE) method. The model solves the Navier-Stokes equations, continuity equation and quasi-static magnetic field equations described in the ALE frame. In order to treat surface tension and time-dependent electromagnetic force on the dynamic boundary, a weak form constraint boundary condition is deduced. This model allows direct simulation of transient flow field, magnetic field and free surface deformation of the liquid metal droplet. The free surface oscillation behavior under different magnetic amplitudes and frequencies are examined. Based on the calculation results, the stability diagram of liquid metal droplet in the magnetic field frequency and magnetic flux density parameter space is proposed.

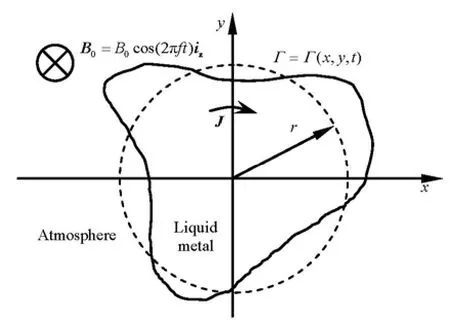
Fig.1 Sketch of the two-dimensional liquid droplet with free surface submitted to a vertical ac magnetic field

1. Formulation of the problem

Consider a thin layer, or a two-dimensional flat liquid metal droplet in the x-yplane with an arbitrarily initial free surface described by a continuous functionΓ= Γ(x, y, t), as shown in Fig.1. The droplet surface area is equal to the one of a circle with prescribed radius of r. It is submitted to a low-frequency AC magnetic field in the vertical direction, or z-direction described asB0= B0cos(2π ft) iz, where B0is the maximum value of the magnetic flux density and is uniform in the whole plane,f is the frequency whilst izis a unit vector along thez-axis. In this case, an electromagnetic force, named as the Lorentz force, will be generated from the interaction between induced electrical currents vectorJ(J being in the xyplane) and applied magnetic field. The electromagnetic force may cause two-dimensional liquid metal motion as well as free surface deformation in thexyplane. In fact, the droplet considered here is an infinite liquid column whose cross section is circular at rest.

1.1 Magnetic field

Because here only low-frequency magnetic field (f≤3.5 Hz) is taken into consideration, quasi-static approximation can be introduced and Maxwell-Ampere’s law and Faraday’s law are consequently written as

where Bz,Hzare respectively the magnetic flux density and magnetic field in the liquid metal, which have only az-direction component. In this case,Bz= Bzizand Hz=Hziz.E is the electric field,uis fluid velocity, and σ,µ0and µrdenote respectively the electric conductivity, permeability in vacuum and relative permeability. Naturally, an electric insulation condition must be satisfied on the free surfaceΓ.

1.2 Fluid flow equations

The Navier-Stokes equations govern the velocity and pressure distribution, namely:

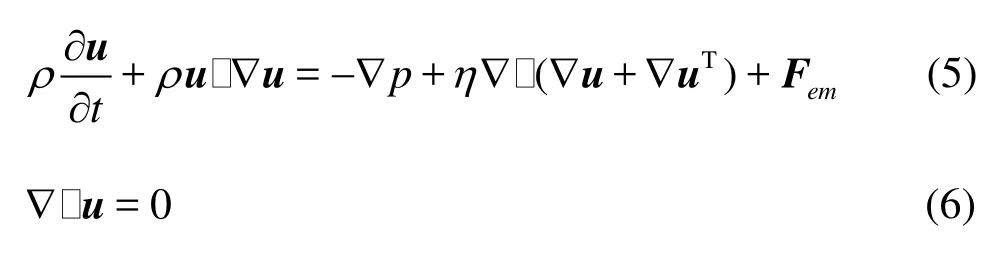
where ρandηare density and dynamic viscosity of the fluid, andpis the pressure field. The body force termFemis the Lorentz force, defined as

This can be determined from the resolution of magnetic field equations.

The condition on the free surface separating the liquid pool from the atmosphere is expressed as

where nis the unit normal directed into the atmosphere. The normal stressf0is caused by curvature-dependent surface tension.

1.3 Moving mesh and boundary conditions for the fluid flow field

A commercial finite element method package, the COMSOL Multiphysics®, was used to solve the Eqs.(3)-(8) on a freely moving deformed mesh, which constitutes the fluid domain. By applying the moving mesh (ALE) module in the package, the deformation of the mesh relative to the initial shape of the domain is computed using the Winslow smoothing method[7], in which two elliptic equations are applied for realizing moving mesh and is pre-defined in the COMSOL graphic user interface. On the boundary, the meshes move at the same velocity of the normal component of the fluid flow field. In the interior of the domain the meshes move in a free displacement way.

The main difficulty of this problem is the implementation of the boundary condition on the dynamic free surface for the fluid flow equations. From the Serret Frenet equation ∂t/∂s = -Cn , wheresis the arc length,Cthe curvature,tandnthe tangent and normal vectors of free boundaryΓ, and the surface tension can be described as Fs=σs∂ t/∂s, which has an opposite direction to the normal vector with a positive surface tension coefficientσs.

where u_testand uT_testare respectively the test functions of the velocity components and their associated tangential derivative (See Appendix).

1.4 Numerical solution

Several kinds of liquid metal initial shape are taken into account (which will be described later), among which a typical one is an ellipse with long half axis of 30.1 mm and short half axis of 29.9 mm (the area is nearly equal to that corresponding to a circle with radius of 30 mm). In this domain, a mesh with 8 762 triangular elements and 97 973 degrees of freedom was created from unstructured triangular grids with fine elements on the boundary, where the maximum element size is 0.3 mm, and grows to coarse ones in the centre, where the maximum element size is 2.0 mm. Some even finer grids were tried in several cases to make sure the calculation results are grid independent. All the calculations began with the state that the liquid droplet is totally static.

The full coupled system of unsteady, nonlinear PDEs from Eqs.(3) to (8) was solved by the finite element method using the COMSOL Multiphysics 3.5a. A time-dependent solver was used together with direct (UMFPACK) linear system solver. The absolute and relative tolerance parameters for the ODE solver were respectively 0.001 and 0.01. Computer with dual-core Intel-i7 M620 processors and 4 GB RAM running in windows 7 64-bit system was employed to obtain solutions presented here. Normally, it took one hour to get a one second whole coupled solution of the liquid metal droplet evolution behavior.

1.5 Model validation

Firstly, the behavior of a free oscillation liquid mercury droplet is calculated using the mathematical model described above when magnetic field B0is set to zero. The physical properties of mercury are listed in Table 1.

Table 1 Physical properties of the mercury

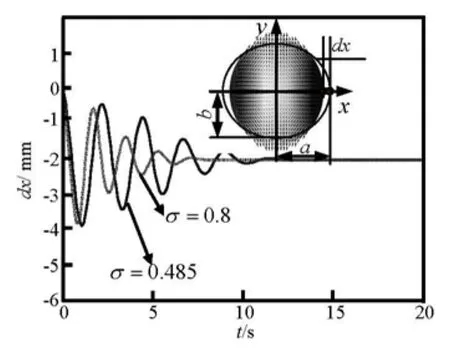
Fig.2 Free oscillation behavior of liquid mercury droplet without magnetic field

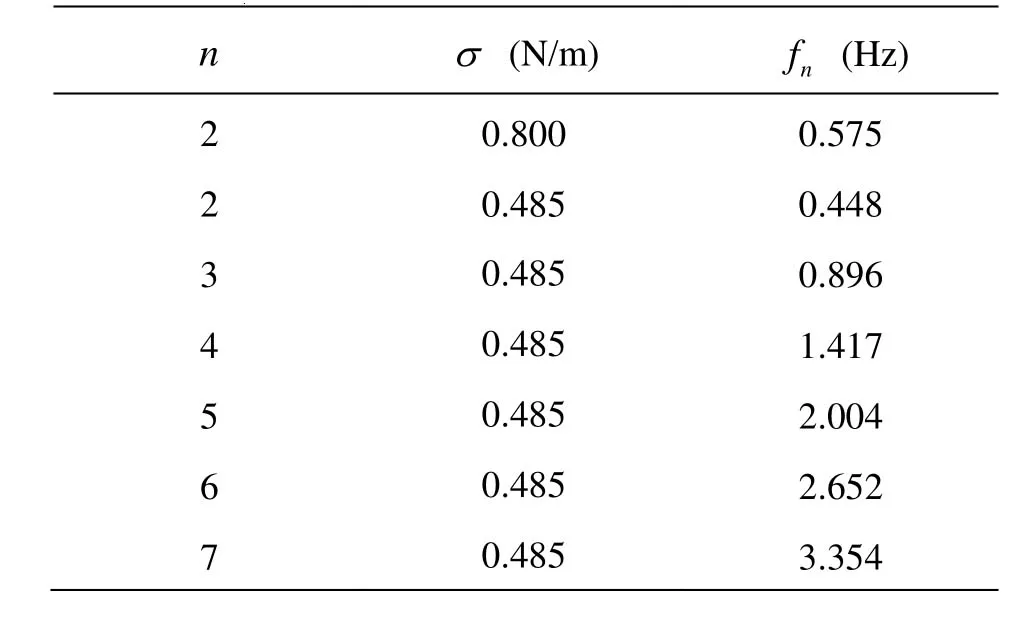
Table 2 Eigen-frequencies fnof a two-dimensional liquid droplet with radius r =30 mm

2. Calculation results and discussion

2.1 Typical dynamic oscillation process of a liquid metal droplet

Beginning from a given initial shape, the transient motion of the liquid mercury droplet can be calculated along with time. Figure 3 shows a typical path in which the droplet evolves to a structured, polygonal shape like wave in the end, where the mode number is 4. In this case, the initial shape is an ellipse with long half axis a =30.1 mm and short half axis b= 29.9 mm, with the maximum value of the magnetic flux density B0=0.014T and frequency f= 1.417 Hz.

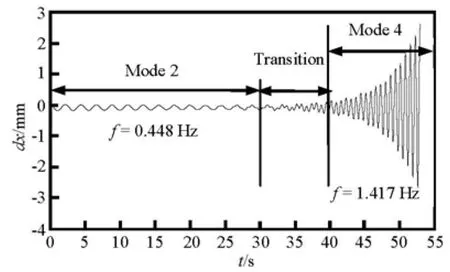
Fig.3 A typical displacements in xdirection of rightmost point under low-frequency magnetic field

According to Fig.3, the curve of rightmost point displacements in the x direction can be divided into three stages. In the first stage, from the beginning to about 25 s, the liquid mercury droplet oscillates in a mode-2 pattern with a frequency of 0.448 Hz, which can be determined by the FFT analysis. The latter frequency is almost equal to the eigenfrequency of the mode-2. The amplitude decreases slowly. In the second stage, named as a transition stage, there are some disturbances emerging from the symmetric movement and the rightmost point oscillates in a way not as regular as in the first stage. Then, in the third stage, this point oscillates with amplitudes increasing at an exponential rate, and the frequency is 1.417 Hz, which is the same as the magnetic field. Finally a mode-4 drop pattern whose eigenfrequency is close to f is excited.

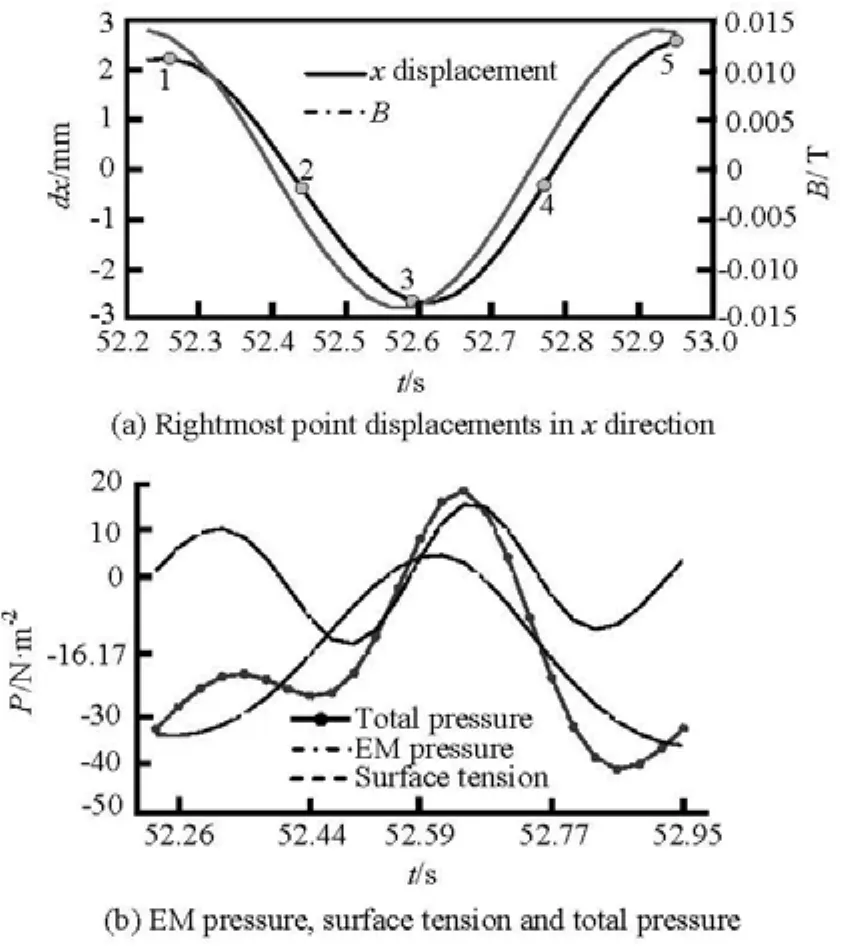
Fig.4 Liquid mercury droplet oscillation behavior in one magnetic field cycle

Figure 4(a) shows the rightmost point displacements in the x direction during one magnetic field cycle for f=1.417 Hz. Figure 4(b) shows the electromagnetic pressure, surface tension and total pressure on the rightmost point along with the time during one magnetic field cycle. One may find that the oscillation frequency of electromagnetic pressure is twice of the magnetic field. The latter result is in agreement with the fact that the electromagnetic forces oscillate at a frequency equal to2f .

Figure 5 shows the topological shape of the liquid droplet at five typical moments as well as the flow field and total electric current density in the whole domain. In which the surface and streamline mean total current density with a maximum value of 1 989.3 A/m2, the arrow means the liquid metal flow velocity with a maximum value of 23.3 mm/s. It canbe found that the liquid droplet has an obvious mode-4 shape at the moment of 52.26 s. At that moment the electromagnetic pressure on the rightmost point has a positive value, which means that its direction is oriented toward the positive x-axis. But its value is lower than the surface tension toward inside there, so the negative total pressure causes the apexes move inward. At the moment of 52.44 s, the droplet reaches its equilibrium shape, and the electromagnetic pressure changes its direction to toward inside, whilst the velocity of this point reaches its maximum value. The point keeps moving inside to form a concave free surface deformation until the moment of around 52.59 s, when the quadrangle shape is inverted, and at that point both the electromagnetic pressure and surface tension have a direction toward the positive x-axis which causes the point to begin to move toward outside. After reaching its equilibrium position (t=52.77 s) finally it forms an apex at the moment 52.95 s and finishes a movement cycle with a little increased amplitude. After this period the oscillation begins a new cycle.

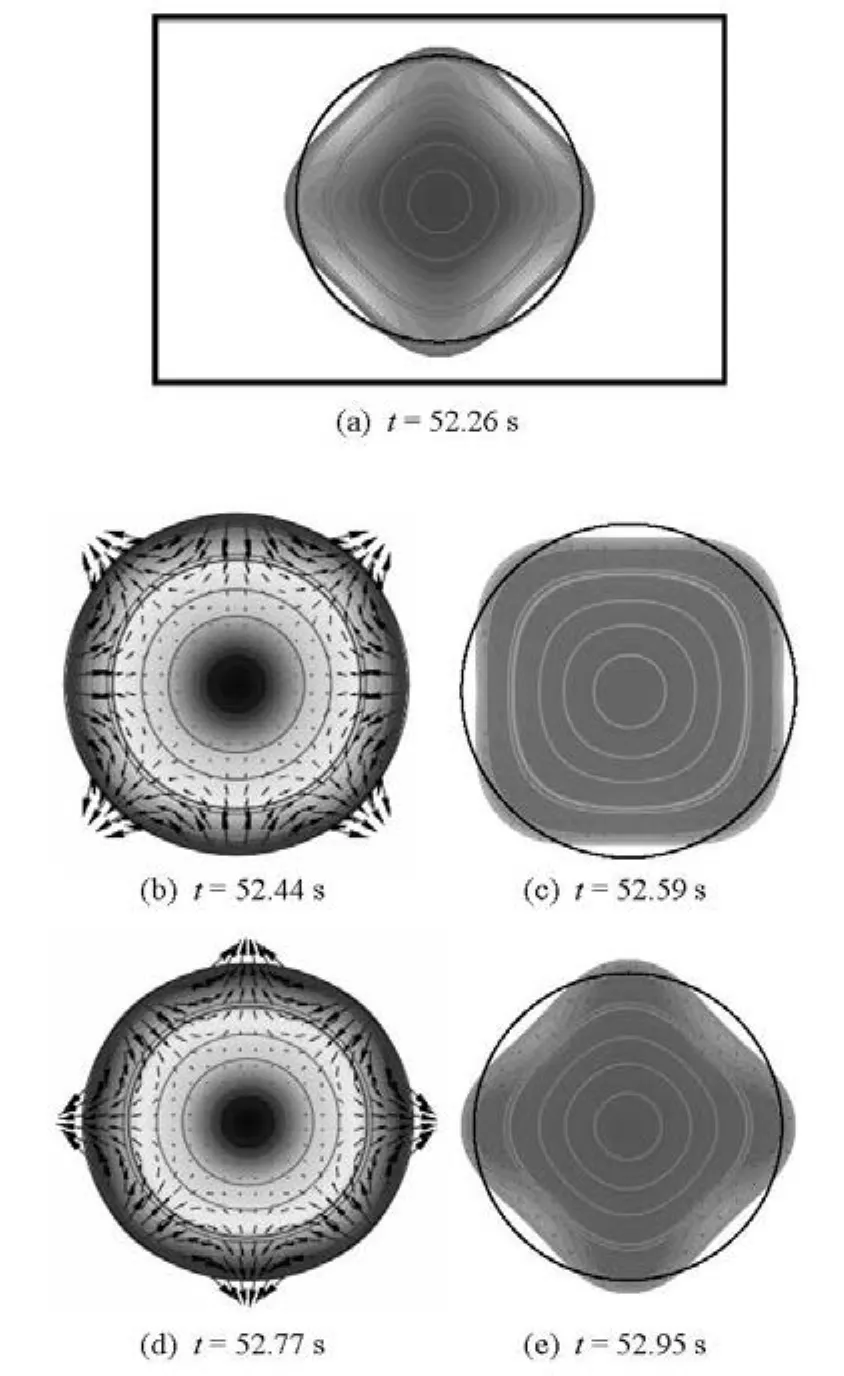
Fig.5 Liquid droplet topological shapes at five typical moments, which are shown in Fig.4, as well as the flow field and total current density

We have applied the same processes under different magnetic flux densities and frequencies. It has been found that at a given magnetic field frequency, there exists a critical magnetic flux density B0_cr. When the imposed magnetic flux density is lower than B0_cr, the liquid droplet admits oscillations which are gradually damped, and finally reaches a static circular state. Some details of the critical magnetic flux density will be given later.

When the imposed magnetic flux density is higher thanB0_cr, a structured polygonal type pattern is triggered, and it evolves with the same ways as shown in Fig.4. The mode numberndepends on the imposed magnetic field frequency. The oscillation frequencies of these motions are exactly the same as the imposed magnetic field frequencies (half of the Lorentz force). This kind of oscillation is analogous to what happened in the so-called parametric instabilities as pointed out in previous work[11-14]. It must be pointed out that in the polygonal oscillation cases, the oscillation amplitudes increase exponentially after every oscillation cycle, which means the velocity in the liquid droplet keep increasing along with time. So a finer grid is needed in order to get converged solution of liquid metal flow field. However, due to our limited calculation capacity it was not possible to continue the computations for longer time period. Practically we stop the calculation once a well identified mode is triggered, so the maximum deformation of the liquid droplet predicted by numerical simulation is not as high as that observed in experiments.

2.2 Effects of initial shape on the evolution process

Several kinds of liquid droplet initial shapes were examined in order to make clear whether the dynamic evolution process depends on the disturbance at the beginning. Figure 6 shows dynamic topological evolutions in one magnetic field cycle of two typical calculation examples when the magnetic flux density is B0=0.012 T and frequency f=2.004 Hz, which is close to the eigen frequency of mode-5.

One of the liquid droplet initial shapes is an ellipse with long half axisa =32 mm and short half axis b=28 mm. The calculation results show that pentagonal oscillation only begins after 65 s. The other initial shape is a circle with a weak irregular disturbance whose boundary is defined as

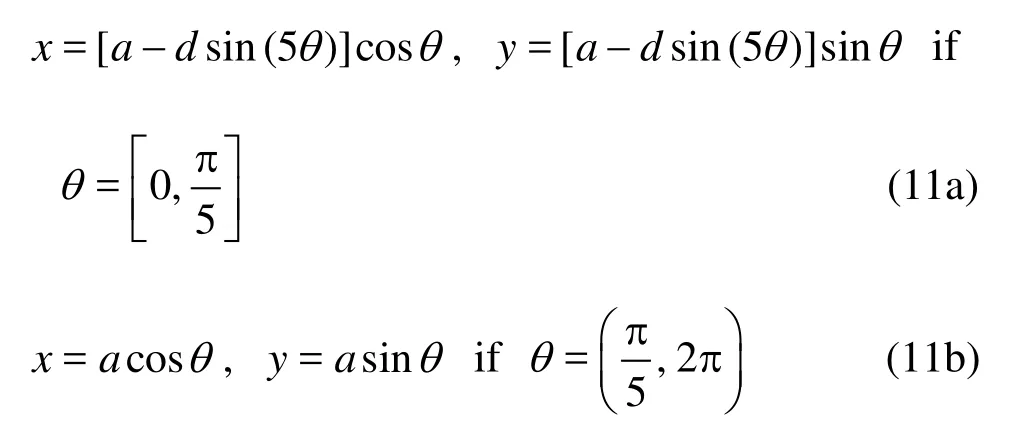
where the disturbance sizes are d =4 mm and radiusa =30 mm.

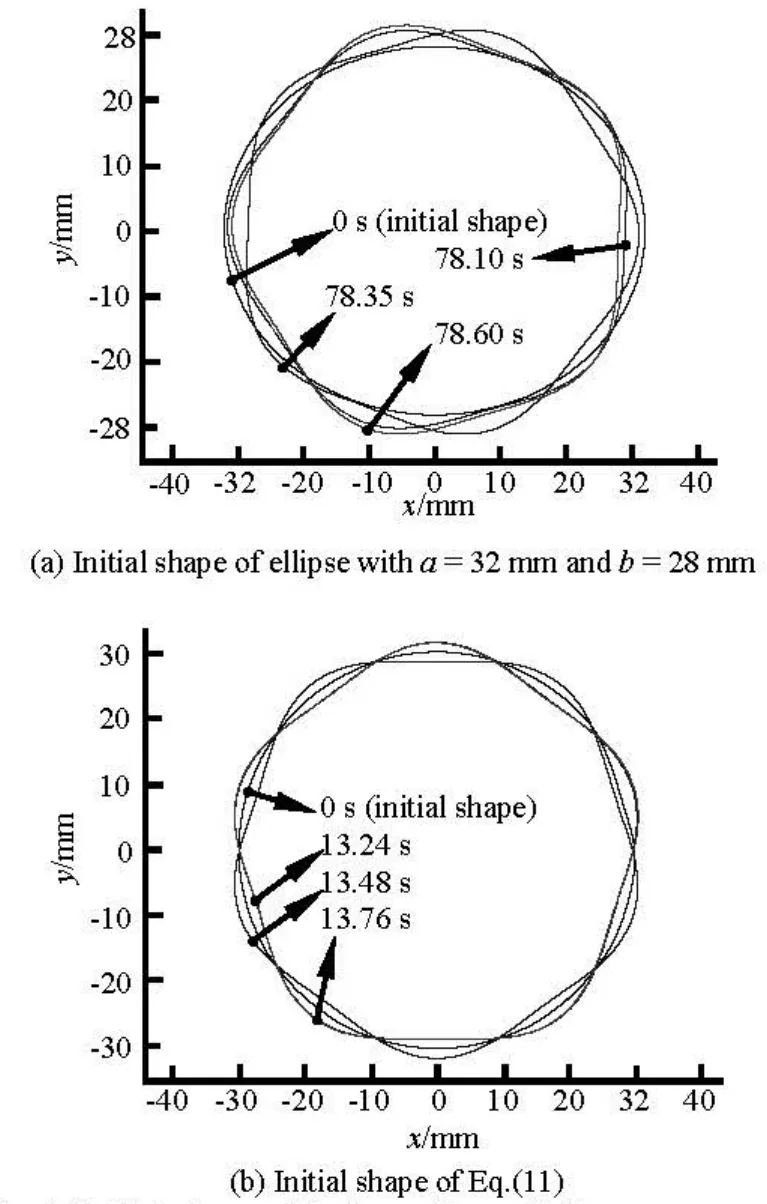
Fig.6 Initial shape effects on the evolution process (B0= 0.012 T,f=2.004 Hz)

The calculation results show that it only need about 10 s before the pentagonal oscillation begins. It is noticeable that the shape of the polygon is nearly the same with different initial shape, even the apex positions are weakly different. Some other initial shapes were examined to make confirmation that the final dynamic oscillation process is independent of initial shape. It is found that it only depends on the magnetic field frequency and the magnetic strength.

2.3 Effects of magnetic flux density on the oscillation

amplitude growth rate

As was described above, once the structured polygonal oscillation modes are excited, the oscillation amplitudes increase exponentially along with time. But under different magnetic flux density the oscillation amplitudes increase at different velocities, which is showed in Fig.7. In that figure the rightmost point displacements in the x direction along with time are still applied when the magnetic frequency f= 1.417 Hz and the magnetic flux density varies from 0.012 T and 0.020 T. It shows that the structured mode-4 oscillations are excited earlier with increasing magnetic field strength. The oscillation amplitudes S are fitted according to an exponentially function as S =exp(k t + q)where the coefficient kis defined as the growth rate of oscillation amplitudes along with time. It is confirmed from Fig.7(b) that the growth rate increases with the magnetic flux density.

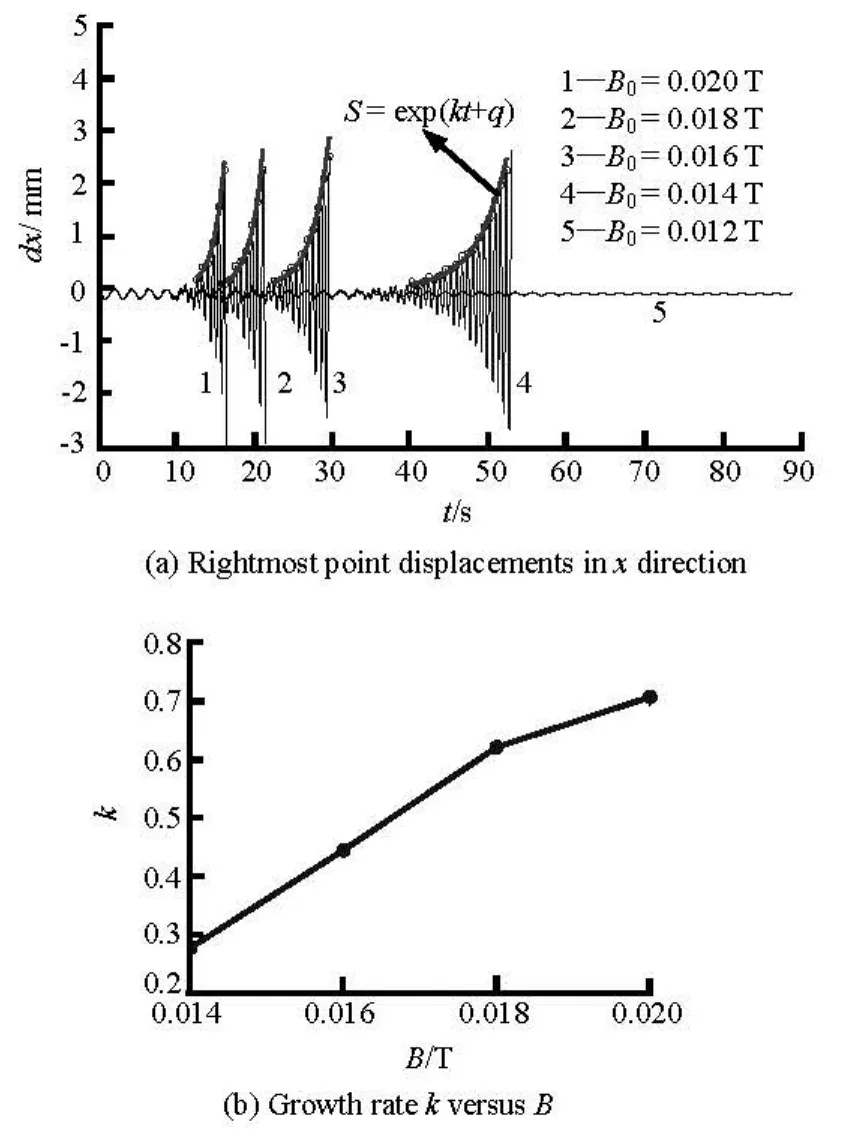
Fig.7 Structured oscillation amplitude growth rate along with time under different magnetic flux densities. Here, magnetic frequency is 1.417 Hz and mode

2.4 Stability diagram in the f-Bparameter space

The appearance of non-symmetric oscillation patterns occurs as soon as the magnetic field exceeds a threshold value. That value depends on the magnetic field frequency. We may construct a stability boundary in the parameter space (B0,f). The computed stability boundary is shown in Fig.8. The boundary consists of several V-shape structures, the so-called“tongues” of instability for various non-symmetric modes. Each tongue has its minimum which corresponds to the eigenfrequency of the modes. Such a behavior is encountered in the so-called parametric instability as previous experimental and analytical works have pointed out[12-15], and also observed in related experiments[6]. This kind of behavior is in agreement with the stability diagram of the Mathieu-type equation which for a given mode n of eigenfrequency fnput forth various tongues for fn,fn/2,fn/3, etc.. The strongest instability appears for fn. It is interesting to notice that when the magnetic frequency is between 0.6 Hz and 0.7 Hz, which is in the region near the half of mode-4, i.e.,f4/2, the mode-4 pattern is triggered instead of mode-2 or mode-3. It may be n otice d that the pres ent mode l is able to c atch notonlythemaintonguecenteredaroundfn,butalso weaker tongues of instability localized at fn/2. The latter results indicate that surface tension is well taken into account in the model, since the eigenfrequency are mainly related to surface tension (cf. Eq.(10)).

Fig.8 Stability boundary of liquid mercury droplet in f-Bparameter space and same calculation examples of various polygonal modes excited in the instability regions

For a given magnetic frequency, for example, f=1.417 Hz, from Fig.7 it can be seen that in the case ofB0=0.012 T, the liquid droplet oscillates with damping amplitude until 90 s, and when B0＞0.014 T the polygonal oscillation modes are triggered in a relatively short time. To find a precise value of B0_crin every given frequency is a time-consuming work, so generally only the range covered the critical point is determined. Here, for example,B0_cris between 0.012 T and 0.014 T whenf=1.417 Hz. All the low limitations of these ranges are determined until the calculation time continues to 120 s and there is no polygonal oscillation modes which are triggered.

Table 3 Calculation parameters for every case shown in Fig.8

In the stability diagram of Fig.8, the low limitation points of every frequency are connected by one fine line, which means that when parameter is below this line, the liquid droplet will be stable finally. The upper limit points of every mode number were connected by one bold line, which means that if magnetic flux density is higher than the value on this line, some kind of polygonal modes will emerge. But we have not calculated the case where the magnetic flux densities are far higher than the up limitation points, this stability diagram is only valid when B0＜0.1 T.

Some typical calculation examples of various polygonal modes are also shown in the Fig.8, and the calculation parameters for every case are listed in Table 3.

Compared with the experimental work[6], the numerical results presented here at least show qualitative agreement, in view of the polygonal oscillation from mode-2 to mode-7 and the structure of stability diagram putting forth tongues of instabilities is localized near the eigenfrequency of each mode. But it must be pointed out that the critical magnetic flux determined by two-dimensional numerical simulation is much lower than in the experiments. That means it is much easier to trigger the non-symmetric mode in the numerical simulation. The possible reasons caused the difference are the following. Firstly, our mathematical model is a two-dimensional one in which there is no gravity, in the experiments gravity is a kind of resistance who tend to restore the droplet to its equilibrium shape during the droplet oscillation. Secondly, in the simulation there is no friction between liquid droplet and the substrate plate and no wetting effects between them either, those are also additional resistance factors. Thirdly, there may be some numerical viscosity during the numerical solution. To improve the results,refiner grid is needed and the corresponding computation is time-consuming, so this work can only give qualitative similarities between the predicted and observed stability diagrams so far.

In the experiments, there is an unstructured regimes characterized by fingers, ejection and void of liquid metal when the magnetic field is too high. In this numerical simulation we could not take this phenomenon into consideration because it is not suitable to simulate a physical process with topological structure variety by applying the moving mesh technique. This is a problem open for the future work.

3. Conclusions

A two-dimensional numerical model based on the finite element method in order to simulate the behavior of liquid metal droplet under a vertical low-frequency magnetic field has been developed. By app lying the ALE method and a weak form constraint boundary condition, the dynamic surface tension and electromagnetic force on dynamic boundary are successfully treated. By using a multi-physics approach, the whole coupled model gives some details on how a liquid two-dimensional droplet is evolving under the action of low-frequency magnetic field.

The simulation results show that at a given magnetic frequency, when the magnetic flux density is lower than a threshold value, the liquid metal droplet is stable, while when the magnetic flux density is higher than a threshold value, a structured polygonal type oscillation will be triggered, and the growth rate of oscillation amplitude increases with increasing magnetic flux density. The oscillation mode number depends on the magnetic frequency and once a polygonal type oscillation is triggered, the oscillation frequency is the same as the magnetic frequency. This process is independent of initial shape. A stability diagram of liquid metal droplet in the magnetic frequency and magnetic flux density parameter space is proposed. The diagram has a structure similar to the stability diagram of the Mathieu-type equation. All these results prove that the appearance of non-symmetric pattern is a type of parametric electromagnetic instability.

Acknowledgments

This work was supported by the China Scholarship Council and Région Rhône-Alpes (France) for supporting Lei’s visiting in Grenoble. The hospitality of SIMAP-EPM is gratefully acknowledged as well.

[1] FAUTRELLE Y., PERRIER D. and ETAY J. Free surface controlled by magnetic fields[J]. ISIJ International, 2003, 43(6): 801-806.

[2] BOJAREVICS V., ROY A. and PERICLEOUS K. A. Magnetic levitation of large liquid volume[J]. Magnetohydrodynamics, 2010, 46(4): 339-351.

[3] ETAY J., SCHETELAT P. and BARDET B. et al. Modelling of electromagnetic levitation-consequences on non-contact physical properties measurements[J]. High Temperature Materiales Processes, 2008, 27(6): 439-447.

[4] ANDREEV O., POTHERAT A. and THESS A. Generation of liquid metal structures of high aspect ratio by application of an ac magnetic field[J]. Journal of Applied Physics, 2010, 107(12): 124093.

[5] KOCOUREK V., KARCHER C. and CONRATH M. et al. Stability of liquid metal drops affected by a high-frequency magnetic field[J]. Physical Review E, 2006, 74(2): 026303.

[6] FAUTRELLE Y., ETAY J. and DAUGAN S. Free-surface horizontal waves generated by low-frequency alternating magnetic fields[J]. Journal of Fluid Mechanics, 2005, 527: 285-301.

[7] HERMANSSON J., HANSBC P. A variable diffusion method for mesh smoothing[J]. Communications in Numerical Methods in Engineering, 2003, 19(11): 897-908.

[8] WALKLEY M. A., GASKELL P. H. and JIMACK P. K. et al. Finite element simulation of three-dimensional free-surface flow problems[J]. Journal of Scientific Computing, 2005, 24(2): 147-162.

[9] AZUMA H., YOSHIHARA S. Three-dimensional largeamplitude drop oscillations: Experiments and theoretical analysis[J]. Journal of Fluid Mechanics, 1999, 393: 309-332.

[10] LAMB H. Hydrodynamics[M]. Cambridge, UK: Cambridge University Press, 1975.

[11] FAUTRELLE Y., PERRIER D. and ETAY J. Free surface controlled by magnetic fields[J]. ISIJ International, 2003, 43(6): 801-806.

[12] SHEN C., XIE W. and WEI B. Parametrically excited sectorial oscillation of liquid drops floating in ultrasound[J]. Physical Review E, 2010, 81(4): 046305.

[13] FAUTRELLE Y., SNEYD A. D. Surface waves created by low-frequency magnetic fields[J]. European Journal of Mechanics B-Fluids, 2005, 24(1): 91-112.

[14] NOBLIN, X., BUGUIN A. and BROCHARD-WYART F. Triplon modes of puddles[J]. Physical Review Letters, 2005, 94(16): 166102.

[15] NOBLIN X., BUGUIN A. and BROCHARD-WYART F. Vibrations of sessile drops[J]. The European Physical Journal Special Topics, 2009,166(1): 7-10.

Appendixes: The free surface boundary condition in weak form of N-S equations

Consider the N-S equation (A1) with boundary condition (A2) in a two-dimensional domainΩwith the boundary Γ,

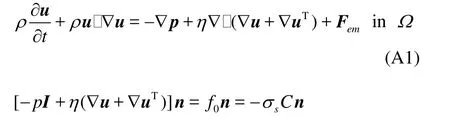
By introducing u _test,v_test, the test functions of velocity components in thexandydirections, the weak form of Eq.(A3) can be deduced by integrating over the domain,

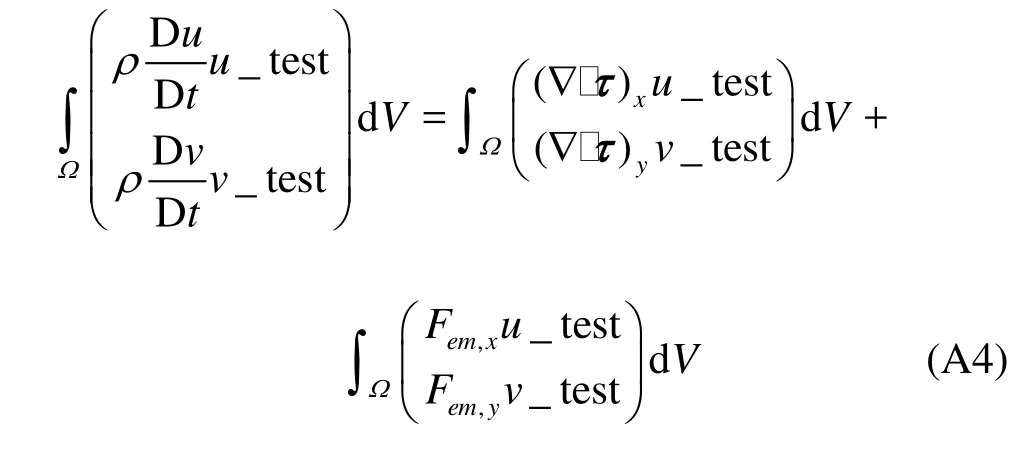
Consider the first term on the right side, then the x component, for instance, becomes

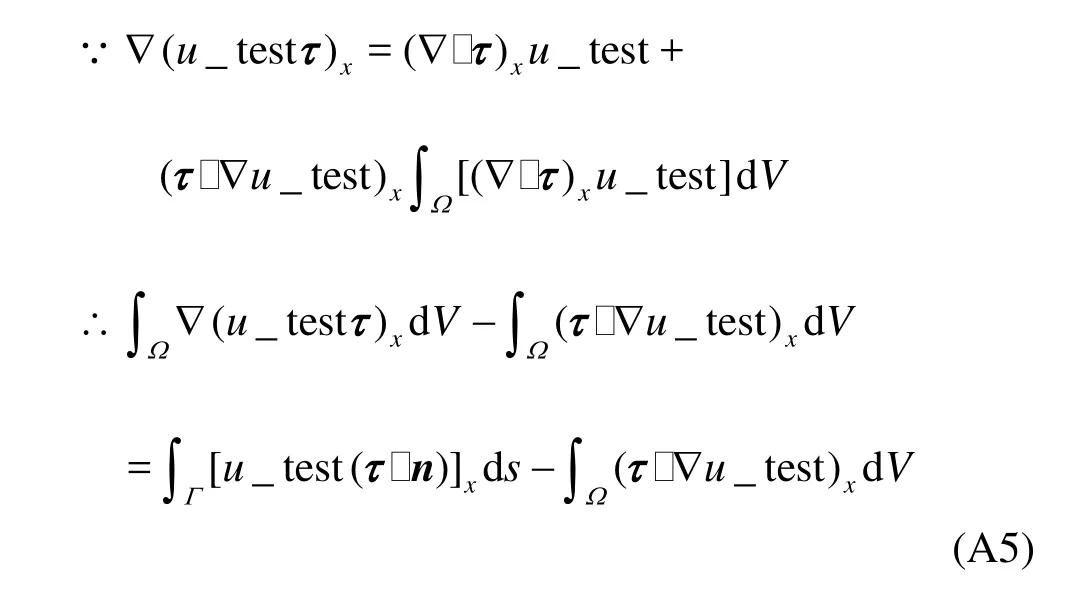
By applying the boundary condition (A2) and the Serret Frenet equation ∂t/∂s = -Cn , we have

By applying the integrating by parts along the boundary, the first item of right side, the surface tension item gives the contribution,

In our case, the boundaryΓis a closed curve, so there is no point contribution, the second term of right side equals turns to zero.

Here uTx _test= tx∂u _test/∂sis the notation in COMSOL frame, which means thexcomponent of the tangential derivative ofu _testwith t=(tx,ty) the tangential vector.u _testand uTx_testare all predefined in that finite element method package.

Hence, finally, the wake form of N-S equation (A3) with boundary condition (A2) is,

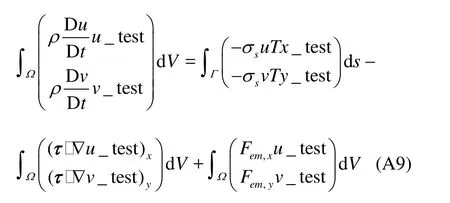
The first term on the right side are the pressure imposed on the boundary caused by surface tension. This expression demonstrates the equivalence of Eq.(A9) as claimed. They are implemented by the weak form constraint condition on the boundary setting in the equations in the COMSOL frame.

10.1016/S1001-6058(13)60367-4

* Project supported by the National Natural Science Foundation of China (Grant Nos. 51274137, 10872123).

Biography: LEI Zuo-sheng (1975-), Male, Ph. D., Associate Professor

GUO Jia-hong,

E-mail:jhguo@staff.shu.edu.cn