蚂蚁优化算法在解决CVRP中的应用

2013-05-28刘瑛

重庆工商大学学报（自然科学版） 2013年4期

刘瑛

（重庆理工大学计算机科学与工程学院，重庆 400054）

运力限制的车辆路径问题CVRP（Capacitated Vehicle Routing Problem）是最基本的车辆路径问题，它在VRP问题的基础上加了限制条件，即所有的车辆对同一商品具有相同的运载能力，每条路线上客户的配送总量要小于车辆的最大运载量。具体描述如下:一个配送中心，对同一种货物，使用具有相同最大运载能力的车辆，完成对需要配送货物数量已知的一组客户（或城市）的配送。问题的目标是使行车路线的运输费用最少。该问题有以下的限制条件:每个客户只能被一辆车服务且只能服务一次;所有的车辆必须从配送中心出席，最后回到配送中心;每条行车路线上的客户的配送总量不能超过车辆的最大运载量;每个客户需要配送的数量必须小于车辆的最大运载量。

简而言之，就是满足上述限制条件，用相同运载能力的车辆花最少的运输费用完成对所有客户点单一货物的配送。国外对物流配送车辆优化调度问题作了大量而深入的研究，该领域的代表人物有Bodin，Christofides，Golden等。在国内，有关车辆调度问题的研究是在20世纪90年代以后才逐渐兴起，比国外相对落后。国内研究对象主要是旅行商问题（Traveling Salesman Problem，简称TSP）、中国邮递员问题（Chinese Postman Problem，简称CPP）、有向中国邮递员问题（Directed Chinese Postman Problem，简称DCPP）等，系统性研究还很少见到。西南交通大学的李军教授和郭耀煌教授对车辆优化调度的基础理论及各类问题进行了系统的研究。李大为等以TSP的最近距离启发式为基础，通过设置评价函数来处理时间窗约束，求解了简单的VRP。另外在利用亚启发式优化算法（如遗传算法、神经网络方法、模拟退火等）对简单TSP的求解取得了一定成果。蔡延光等应用模拟退火法针对满载问题进行了求解。总体来说，目前我国对车辆调度问题的理论研究仍相对薄弱，需要进一步研究。

1 数学模型

式（1）为问题的目标函数，表示完成所有客户配送，所用车辆行驶路线长度总和的最小值;式（2）表示第k辆车的配送客户的货物总量不能超过车辆的最大运载量q;式（3）表示每个客户i只能让一辆车进行配送服务，并且只能被服务一次;式（4）表示每辆车k，最多只能开往客户j一次;式（5）表示每辆车k最多只能离开客户i一次式（4）和式（5）结合在一起说明每辆车k对每个客户点进入一次，就必须离开一次，并且最多只能访问一次。

2 算法设计

2.1 基本蚂蚁算法求解CVRP问题的模型

蚂蚁算法解决CVRP问题，关键在于单只蚂蚁一次迭代如何构建整个问题的一个可行解。在一次迭代中，蚂蚁通过正确选择下一个可以访问的客户来进行移动，在选择下一个客户时，由于车辆运载能力限制，没有客户可选择时，就选择配送中心，然后开始下轮的蚂蚁循环，直到所有客户都被访问，寻找到问题的一个解，然后更新残留信息素完成一次迭代。蚂蚁在选择下一个可访问的客户时受到以下两个因素影响，一个是与连接当前客户i到选择客户j这条边相关的残留信息素τij，另一个就是启发信息ηij，一般的，启发信息ηij=1/cij，cij为两点的距离。在可访问的客户节点集allowed={j∈V，j满足限制条件}∪{0}，依据随机性原则选择客户j，蚂蚁k从客户i出发下一站选择客户j的概率的计算方法如式（6）:

α为残留信息素的相对重要程度，β为启发信息（也叫可见性）的重要程度，通过调整α，β来决定残留信息素和启发信息在选择概率的相对作用大小。

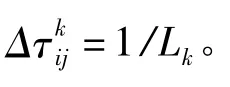
蚂蚁算法首先进行初始化，蚂蚁数量m设成和客户的数量n相等，每只蚂蚁在不同的客户点，算法初始化后，将上面两个步骤构造解路径和更新信息素循环执行指定的次数Imax就是基本的蚂蚁算法模型。

2.2 局部搜索优化

2－opt启发式搜索是通过对边的交换产生一个2－opt解路径，所谓的2－opt解路径就是通过交换任意不相邻的两边来缩短解路径的长度，直到以这种方式不能再缩短解路径为止。人工蚂蚁可以将2－opt搜索优化用到构造解的过程中。在每次迭代过程的最后，用2－opt对每只蚂蚁找到车辆路径进行局部搜索优化，然后再计算所有路径的长度，对优化后路径进行信息素更新。在蚂蚁算法中引入2－opt搜索优化过程，可以大大提高局部解路径的质量，加快蚂蚁算法的收敛速度。

2.3 问题相关的算法

CVRP有一些特点能够用到蚂蚁算法中帮助改进蚂蚁算解路径的质量。在CVRP问题，不仅两个客户的相对路径对蚂蚁搜索路径很重要，而且这两个客户与配送中心的相对位置也很重要。利用节约量μij可以判断连接客户i和客户j的可行性，μij=cio+coj－cij，节约量越大，表示在客户i选择客户j越好，将节约量与蚂蚁算法的转移概率联系起来，节约量越大，选择的概率就越大，即pij～，这样就能提高蚂蚁系统可行解的质量。

CVRP有运力限制的约束条件，因此，高的运力利用率有利于找到问题的满意解。设qi是车辆在客户i的总运载量，包括客户i的需要运输的货物量，从客户i到客户j的运力利用率kij=（qi+gj）/q，将运力利用率和选择概率联系起来，运力利用率越大，选择概率越大，即pij～，将节约量和运力利用率加入大选择概率的求解过程中来对蚂蚁算法进行优化，这样在客户i选择客户j的选择概率公式（8）如下:

3 实例求解与分析

3.1 标准数据集测试

采用关于CVRP问题的标准测试数据集E－n22－k4来测试算法，对基本蚂蚁算法求解车辆路径问题的性能进行分析。E－22－k4问题为22阶CVRP，包括一个配送中心，21个客户，至少要用4辆车进行配送，每辆车的最大运载量为6 000，目前的最优解为375。对基本蚂蚁算法（AS），进行局部搜索优化的蚂蚁算法（AS+LS），加入精英蚂蚁的蚂蚁算法（AS+E），加入与问题相关参数的算法（AS+P），以及融入所有改进的综合蚂蚁算法（AS+ALL）进行数据测试分析，分析各自的特点。AS+LS，AS+E，AS+P都是在基本蚂蚁算法基础上进行某一方面的改进。最后，将AS+ALL用来解决几个标准的CVRP数据模型来验证算法的可行性。再对基本参数 α，β，ρ，σ，m等进行初步性能测试之后，最终确定Imax=5 000，α =1，β =1，ρ=0.99，γ =1，σ =8，m=10。

表1 几种蚁群算法的比较

分析实验结果（表1），AS算法能够接近模型的最优解835，但是解的质量还是有些不够理想，平均解只有856.8，稳定性较差，最优和最差相差17，收敛速度差，平均需迭代1 737次。AS+LS算法将局部解进行交换优化，使得算法有了很大改进，平均解达到843，算法比较稳定，最差的解为843，迭代的次数降低，实际上，通过局部优化将局部解优化，在优化后的路径上释放信息素，使得整个蚂蚁的搜索的过程向着更接近最优解的搜索空间进行搜索，而且当蚂蚁迭代到一定的次数后，结果变的稳定，很难再找到更优解，这时只能通过局部搜索优化来改进解。AS+E算法使得算法是当前蚂蚁的搜索空间向着当前最好解的方向收敛，加快了蚂蚁算法的收敛速度，因此，平均解达到846.7，解的质量相对AS有所提高，数据中的平均迭代次数为2 047，相对AS有所提高，因为算法搜索较好解是一个收敛过程，在聚集信息素，数据中最好解为846，而最差解为847，由于算法快速向着目前最好解进行收敛，导致算法在局部最优解的停滞。AS+P算法的解结果也比AS有了大的提高，平均解为847.9，这说明在加入了与问题相关的信息后，这里主要是指车辆路径问题中加入了节约量，使得搜索过程向着满足问题限制得最短路径收敛，和AS+E一样，AS+P也会陷入停滞。将上述得改进措施都加入基本蚂蚁算法中，蚂蚁算法在稳定性和最优性都得到了提高，达到了较接近问题最优解的837，并且比较稳定，平均解也是837，收敛速度也比AS有了明显的改进，迭代次数为1 097次。