预弛度接触网静态形状解析计算
2013-05-28关金发吴积钦
关金发,吴积钦
0 引言
简单链形悬挂接触网由于其具有高度一致、弹性均匀、弓网动态稳定性好等特点,具有良好的受流性能,因此,在干线和城市轨道交通的电气化铁路大量使用,目前,简单链形悬挂在世界许多国家均有应用,如:法国、中国、日本等。
简单链形接触悬挂主要由承力索、接触线、吊弦、支持与定位装置、补偿装置等结构组成。由于其跨度大、线索的截面小,简单链形接触悬挂表现出张力弦的特性尤为明显,故简单链形悬挂多以索网找形的方法计算其静态形状。
对链形悬挂接触网的静态形状计算研究的文献很多,如:文献[1,2]利用力矩平衡法求承力索的弛度;文献[2~4]利用有限单元法对接触悬挂进行索网找形;文献[5]虽考虑了接触线受力,但要么把接触线看作直线单元,要么把接触线看作一个整跨距抛物线单元,并未给出接触线预弛度的计算方法[5~8]。
结合以上对简单链形悬挂的计算,笔者研究提
出以抛物线为基本单元、经典力学为计算依据、考虑接触线预弛度的接触网静力学解析计算方法,计算受自重影响的简单链形接触悬挂静态形状,该计算方法与有限单元法进行对比,验证其有效性、准确性。
1 抛物线单元计算
该研究把链形悬挂接触网看作悬索结构,目前主要的索单元有2 节点直线杆单元、2 节点抛物线索单元、2 节点悬链线索单元和多节点等参索单元,文献[1、6、9、10]通过计算验证,在小跨距的情况下,抛物线单元与悬链线单元的弛度基本一致,又考虑直线杆单元的几何等效性差,悬链线单元中的双曲余弦、多节点等参索单元计算复杂,故该研究所有计算均基于抛物线单元。
悬索的抛物线单元是一种基于均布载荷的2节点单元,抛物线的单元有等高悬挂与不等高悬挂2 种情况,如图1和2 所示。使用抛物线单元需满足的前提条件:
(1)假设线索的水平方向张力相等,即图1和图2中Tb= Ta= T(线索额定张力)。
(2)假设线索在图1和图2中坐标平面内的曲线成抛物线函数。
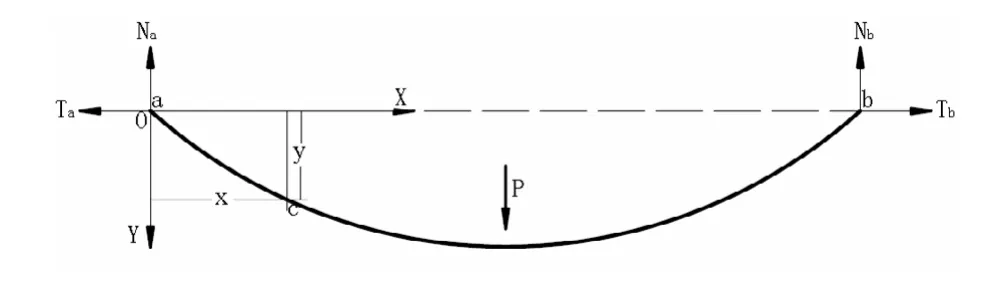
图1 等高悬挂抛物线单元示意图

图2 不等高悬挂抛物线单元示意图
由力矩平衡不难推导等高悬挂和不等高悬挂抛物线单元的弛度计算公式:

2 受自重影响的接触网静态形状计算
简单链形悬挂的跨中弹性比较大,为得到更小的弹性不均匀系数,接触线需要预留一定弛度。SNCF(法国铁路公司)通过实验研究表明预留跨距的0%~0.05%弛度有利于弓网高速运行[11]。而应用简单链形悬挂的中国京津城际高速铁路的接触线预弛度则取跨距的0.05%。故在接触网设计时须考虑预弛度的接触网静态形状。
分析受自重影响的预弛度简单链形悬挂静态形状,静态计算的流程如下:
简单链形接触悬挂受力分析→确定力的数量和方向→接触线预弛度曲线→确定接触线吊弦点高度→确定吊弦节点力→吊弦间隔接触线静态形状计算→吊弦间隔承力索静态形状计算→确定承力索吊弦点高度。
简单链形接触悬挂静态形状计算有2 点假设:
(1)由于第1 吊弦至定位点的弹性较小,该段不需要预留弛度。
(2)承力索与接触线悬挂点只有沿张力T 方向的自由度。
2.1 接触线静态形状计算
预弛度接触线静态形状计算由3 个等高悬挂和若干个不等高悬挂抛物线单元组成,如图3所示。

式中,L 为跨距值,m。注意,若f 取0,则为无预留弛度接触线。



图3 简单链形接触悬挂受力示意图
以图3中2 吊弦节点间距 qp^^ 为例,计算该段静态形状。在p 点处建立局部坐标系x′o′y′,用一个不等高悬挂抛物线单元等效真实弧长 qp^^ ,由于yi-1、yi值已知量,该抛物线单元的水平距离为l=xi-xi-1,高度差h=yi- yi-1,代入式(2),得第i-1根吊弦与第i 根吊弦之间的接触线静态形状:
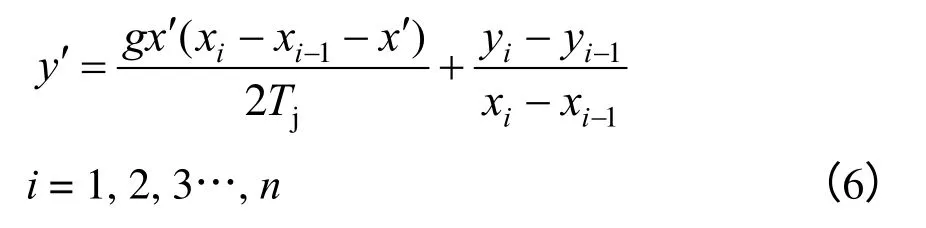
式(6)中,g 为接触线的单位长度自重,把式(6)转化为整体坐标系xoy,得:
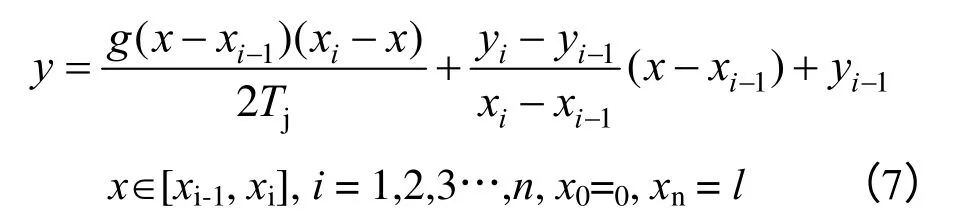
至此,吊弦间距内的接触线静态形状均确定。
由定位点至第1 吊弦或最后一根吊弦处的静态形状为2 段等高悬挂抛物线单元,其静态形状按式(1)计算。
吊弦除承担接触线自重外,还需包括自身重量,由于吊弦较轻,因此假设每根吊弦的自重相同,均为w,故第1 吊弦力为

第i 吊弦力为

第n 吊弦力为
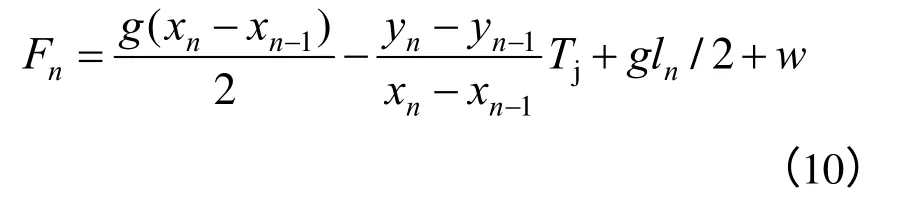
2.2 承力索静态形状计算
承力索受自重和吊弦力的影响,以一悬挂点为原点建立坐标系eod(图4),假设承力索的静态形状由若干不等高悬挂抛物线单元组成,每一吊弦节点的位置为(e1、d1),…,(ei、di),…(en、dn),其中e1~en为吊弦水平位移,为已知量。

图4 预弛度接触线静态形状示意图
由于静态平衡下抛物线单元节点处的力矩为0,故把悬挂点A 和吊弦点1 之间的承力索看作1个抛物线单元,由力矩平衡计算吊弦节点1 的垂向位移:

把悬挂点A 和吊弦点i 之间的承力索看作1 个抛物线单元,计算吊弦节点i 的垂向位移:

至此,承力索的每个吊弦节点坐标已求出。承力索的弛度计算同式(7),在eod 坐标系中,承力索的静态形状函数:
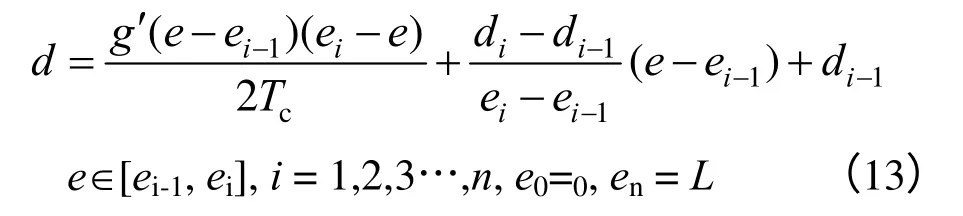
通过上述公式得出接触线与承力索的每一吊弦点位置,故联合式(7)、式(13)很容易就计算出吊弦的长度:

式中,D 为结构高度。
3 计算示例
下面以京津城际接触网为例验证该计算方法的准确性,京津城际接触网具体参数见表1。

表1 京津城际接触网设计参数表
以L= 48 m 为标准跨距,此时吊弦间隔为 9.5 m,吊弦数为5,根据第2 章方法,计算受自重影响的接触网静态形状。
首先,对京津城际接触网计算预弛度 f=0.024 m,代入式(4),得P= 3.59 N/m,然后将吊弦水平距离代入式(5),得出接触线吊弦节点的坐标,见表2。最后由式(8)—式(10)计算接触线吊弦节点力,见表2。
将吊弦节点力和承力索参数代入式(11)和式(12),计算承力索吊弦节点的位置,见表3。由
式(14),计算出每根吊弦的长度,见表4。

表2 接触线吊弦节点坐标及节点力一览表
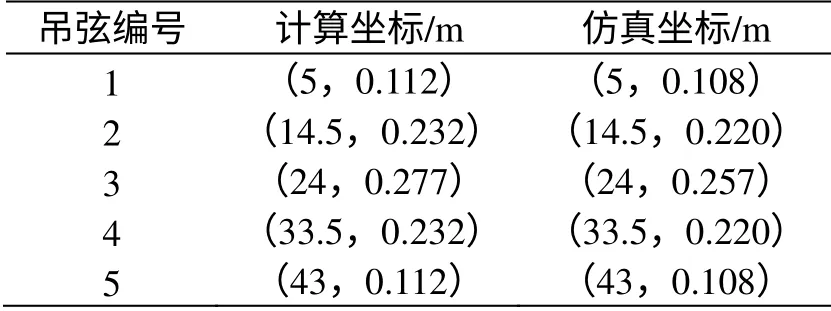
表3 承力索吊弦节点坐标一览表
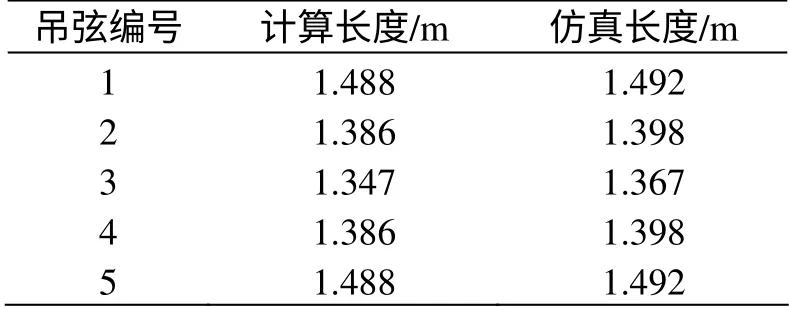
表4 吊弦长度一览表
接触线的静态形状由2 个等高悬挂和4 个不等高悬挂抛物线单元组成,根据式(1)、式(7),绘制接触线的静态形状,见图5。承力索的静态形状由6 个不等高悬挂抛物线单元组成,根据式(13),绘制承力索的静态形状,见图6。

图5 受自重影响的接触线静态形状曲线图
利用有限元法,对同样参数的接触网建模,接触线、承力索、吊弦均使用拉索单元,接触线、承力索一端悬挂点固定,一端悬挂点加补偿力,接触线建立481 个节点、承力索建立481 个节点,吊弦单独使用一个元素,最后进行重力场加载,接触网的静态形状仿真曲线见图5、图6。仿真的结果见表2—表4。

图6 受自重影响的承力索静态形状曲线图
4 结论
(1)上文以抛物线单元为基础,给出受自重影响简单链形接触悬挂静态形状的计算流程,推导出不同坐标系下的预弛度接触线、承力索静态形状的计算公式,并给出吊弦长度计算公式。
(2)应用该计算方法计算京津城际接触网受重力场影响下的静态形状,对比有限元仿真结果,得出由计算得到的接触线静态形状与仿真结果非常接近,承力索的静态形状计算结果只在垂向位移处比仿真结果稍大,但差距很小,在10-2数量级上,满足工程应用的要求。通过对比有限元仿真,验证了本文所述的计算方法的准确性。
(3)该研究能对简单链形接触网进行吊弦预配计算,能很好地指导接触网的设计、施工。
(4)该计算方法不仅对预弛度接触网适用,对无预弛度接触网同样适用。
[1]于万聚.接触网设计及检测原理[M].成都:西南交通大学出版社,1991.
[2]J.Benet.A tool to calculate mechanical forces on railway catenary, Computers in Railways VII [M].WIT Press, 2000:537-544.
[3]方岩.高速接触网整体吊弦预配[J].西南交通大学学报,2010,(5):763-767.
[4]刘大勇.基于索网找形的接触网吊线长度计算方法研究[D].西南交通大学,2009.
[5]阮杰.电气化高速铁路接触网静态模型的建立[J].铁道学报,2012,(34):20-25.
[6]Sung Pil Jung.Estimation of Dynamic Contact Force Between a Pantograph and Catenary Using the Finite Element Method [J].Journal of Computational and Nonlinear Dynamics, 2012(7):041006-1-13.
[7]Yong Hyeon Cho.Influence of contact wire pre-sag on the dynamics of pantograph-railway catenary [J].International Journal of Mechanical Sciences, 2010:1471-1490.
[8]J.Benet.Advanced algorithm to calculate mechanical forces on a catenary, Computers in Railways IX, [M].WIT Press, 2004:854-868.
[9]程大业.悬索结构分析的精确单元方法[D].清华大学,2005.
[10]苏文章.悬索结构的非线性有限元分析[D].重庆大学,2005.
[11]Kiessling.Contact Lines for Electric Railways [M].Publicis Publishing, Erlangen, 2009:158.
[12]TB 10009-2005 中华人民共和国铁道部[S].北京:中国标准出版社,2005.
