直升机使用吊放声纳搜潜作战的策略研究
2013-05-28倪春光陈迎春王先华
倪春光, 陈迎春, 王先华
直升机使用吊放声纳搜潜作战的策略研究
倪春光, 陈迎春, 王先华
(水声对抗技术重点实验室, 广东 湛江, 524022)
研究了温跃层海洋环境条件下直升机使用吊放声纳搜潜的作战策略, 首先建立了直升机和潜艇的运动学模型、吊放声纳的探测模型和水声传播模型, 后者考虑了声速剖面和海底参数的影响。基于蒙特卡洛仿真定量分析了直升机时延、吊放声纳优质因子、吊放深度和任务时间等关键作战要素对反潜效果的影响。
直升机; 吊放声纳; 潜艇; 作战策略
0 引言
潜艇以极强的隐蔽性, 成为现代战争中极具威胁的突袭手段, 具有巨大的战术和战略威慑意义。战争中, 及时有效地探测敌方潜艇的位置、航行深度和速度等特征参数, 是投放空投鱼雷反潜的先决条件之一。反潜直升机是当今最有效的反潜兵力之一, 它具有机动性能好、反应速度快、受威胁小等优点[1]。目前世界各国海军的大、中型反潜水面舰艇普通装备有反潜直升机, 舰载直升机已成为水面舰艇反潜的重要手段。吊放声纳作为航空搜潜的重要装备, 以尺寸小、重量轻、使用机动灵活等优点而在实际作战训练中得到广泛使用。使用吊放声纳搜索和跟踪潜艇是航空反潜的主要手段之一[2]。本文主要研究存在温跃层条件下直升机使用吊放声纳搜潜的作战使用策略。
1 潜艇与直升机的对抗策略模型
1.1 潜艇运动学模型

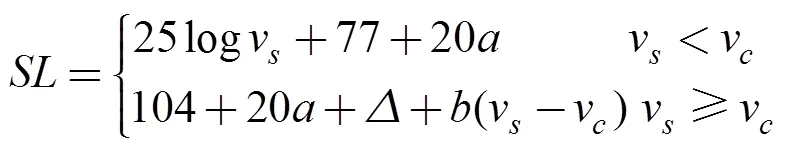
1.2 直升机运动学模型
反潜直升机使用吊放声纳搜潜时, 常用的搜索算法有方形、扇形、锯齿形、矩形、螺旋线形和扩展螺旋线形。方形搜索算法的航线如图1所示, 其中:为吊放间距, csp为起始搜索点。
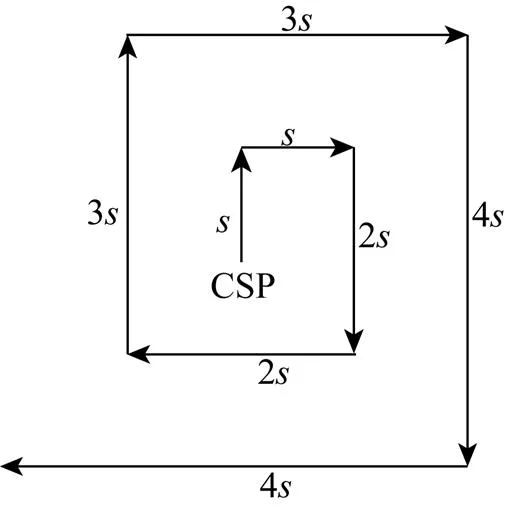
图1 方形搜索算法示意图
1.3 吊放声纳探测模型
反潜直升机完成一次探测所需的平均时间称为搜索周期, 它包括水下分机下放时间、声纳搜索时间、水下分机提升时间、直升机飞向下一个吊放点所用时间以及直升机在单个搜索周期内转弯、悬停所耗费时间。直升机使用吊放声纳时主要考虑吊放深度的影响。

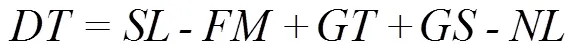
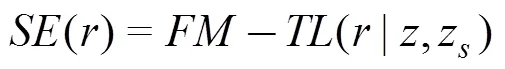
1.4 水声传播模型
声波在海洋中的传播满足基本的波动规律, 即波动方程, 所有声场模型的理论基础均为波动方程。波动方程从基本的状态方程、连续方程和运动方程中导出。海洋声场理论的核心问题就是求解满足相应边界条件的波动方程

严格求解方程(4)是复杂的甚至是不可能的。为了得到一般条件下波动方程的解只能利用数值算法。根据使用的特定几何假设及解的表达式, 波动方程有多种类型的数值解。不同解的形式形成了不同的声场模型。
对水平变化的问题, 抛物近似方法被证明是一个有效的手段。抛物方程法(parabolic equation, PE)最初是由Tappert引入海洋声学的[5]。之后, PE技术发展得非常快, 并已经成为解决水平变化的水声问题最有效的方法之一。目前已有的2D PE声场计算程序很多, 关于PE进展可参阅文献[6], 如UM模型[7]、FE模型[8]和RAM模型[9]等。在计算精度上, RAM等同于其他高阶PE解, 但在同样的计算精度要求下, RAM允许更大的计算步长, 从而大为减少了计算时间[10]。鉴于RAM的诸多优点, 本文主要采用RAM模型来进行声场的数值预报。
2 仿真结果与分析
2.1 参数设置
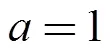
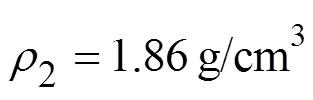
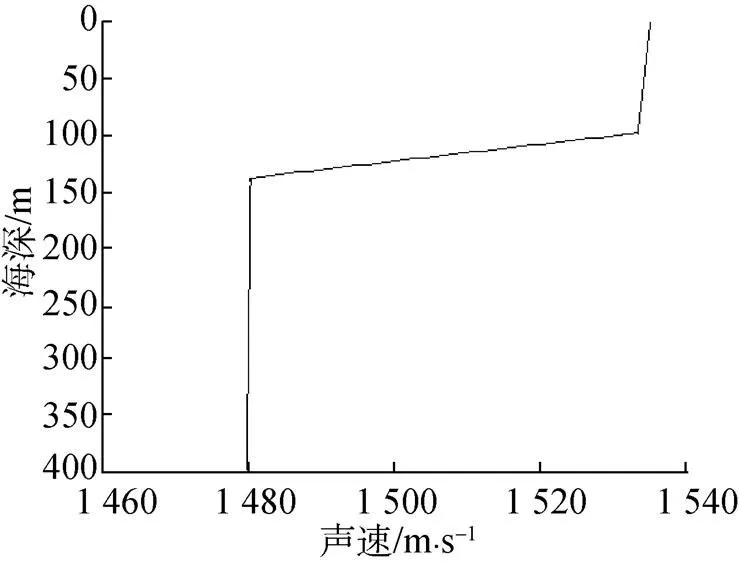
图2 声速剖面图
2.2 声场计算结果
在计算过程中, 设声源深度srcDep={10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 105, 110, 115, 120, 125, 130, 135, 140, 150, 160, 170, 180, 190, 200, 210, 220, 230, 240, 250, 260, 270, 280, 290, 300, 310, 320, 330, 340, 350, 360, 370, 380, 400} m。设接收深度recDep={50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180, 200, 250} m, 利用MOATL程序计算不同距离上的传播损失, 其中直升机吊放声纳的吊放深度在50 m、120 m和150 m时在6 km距离上传播损失如图3所示。
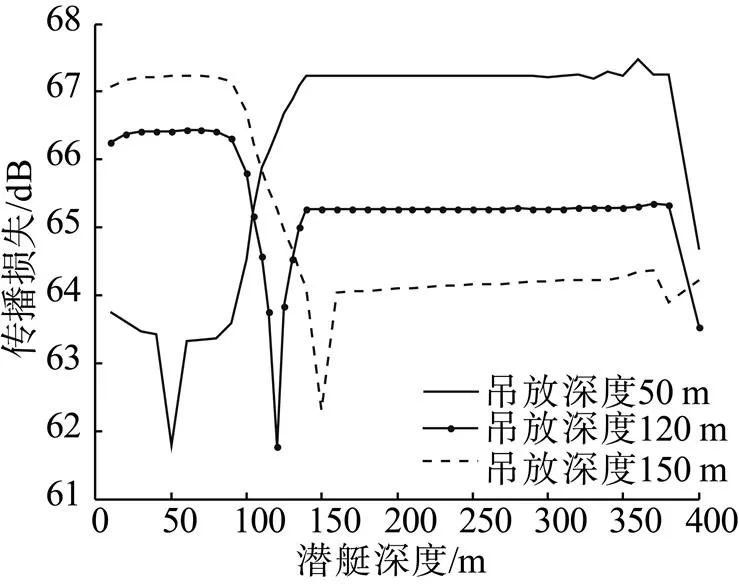
图3 吊放深度在50 m、120 m和150 m下的传播损失
2.3 仿真过程
仿真过程如下。
1) 随机产生10000组潜艇的运动策略: 速度在[6, 20] kn之间均匀产生, 航向在[0, 360]°内均匀产生; 航深在srcDep数组内随机选择。
2) 随机产生10000组直升机的运动策略: 吊放声纳的吊放间隔系数在[1.2, 2.0]内随机产生, 吊放深度在recDep数组内随机选择。
3) 潜艇每组策略与随机抽取的1000组直升机策略逐一对抗, 累计对抗的胜负结果。
4) 直升机每组策略与随机抽取的1000组潜艇策略逐一对抗, 累计对抗结果。
5) 结果判定: 潜艇和直升机每分钟更新一次位置, 计算两者之间的距离; 根据潜艇航速修正吊放声纳的优质因子, 根据潜艇深度(声源深度)和吊放声纳深度(接收深度)以及两者之间的距离查表得到传播损失。如果优质因子大于传播损失则潜艇被发现, 直升机获胜, 否则继续。若5 h后声纳仍未发现目标, 则潜艇获胜, 对抗结束。
2.4 结果分析
从预警系统发现潜艇的概略位置到直升机赶赴该位置的时间定义为时延。时延对直升机发现潜艇的概率影响非常大, 如图4所示, 其中折线为直升机发现潜艇的概率。这就要求反潜预警系统具有快速反应能力。

图4 时延对直升机发现潜艇概率的影响
吊放声纳的优质因子对直升机发现潜艇概率点影响也非常大, 如图5所示。
优化得到直升机吊放声纳的吊放深度(m)分别为: 60, 90, 130, 70, 70, 120, 180, 140, 150, 70, 130, 160, 150, 80, 170, 150, 90, 50, 150, 160, 110, 110, 90, 200, 50, 140, 100, 170, 160, 90。这说明吊放声纳的吊放深度不能固定, 应该在允许的深度范围内随机变化。

图5 吊放声纳优质因子对直升机发现潜艇概率的影响
直升机能执行任务的时间长度也影响了发现概率, 如图6所示。可以看出, 任务时间达到190 min左右后发现概率的变化不太明显, 这是因为此时目标的散布范围非常大了。
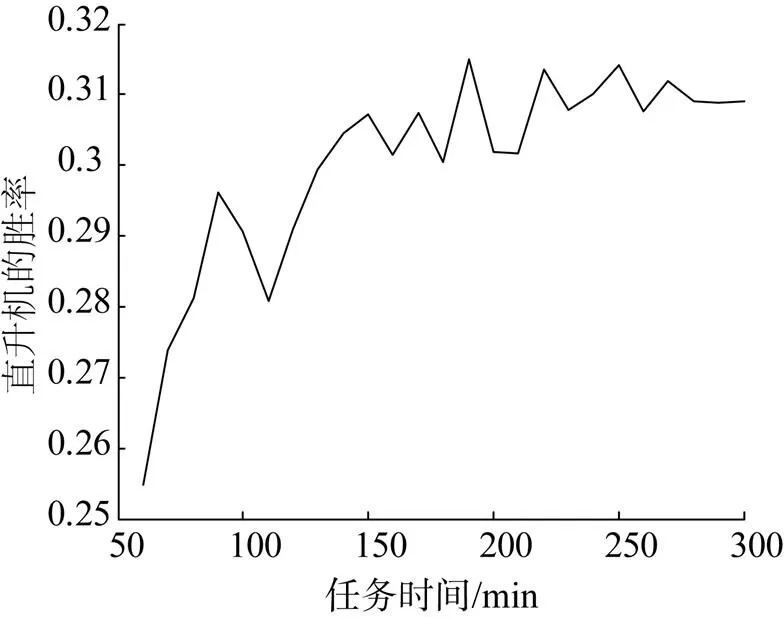
图6 任务时间对直升机发现潜艇概率的影响
3 结束语
本文建立了直升机和潜艇的运动学模型、吊放声纳的探测模型和水声传播模型, 基于蒙特卡洛仿真定量分析了温跃层环境下影响直升机吊放声纳反潜效果的关键作战因素。
下一步将研究直升机不同搜索模型对发现概率的影响, 并从博弈的角度研究直升机以及直升机编队搜潜的作战策略及其优化。
[1] 汤智胤, 何琳. 基于直升机声纳探测的潜艇被发现概率仿真[J]. 系统仿真学报, 2008, 20(17): 4751-4755. Tang Zhi-yin, He Lin. Simulation Research of Counter- detection Probability of Submarine Based on Antisubmarine Helicopter Sonar Detection[J]. Journal of System Simulation, 20(17): 4751-4755.
[2] 高学强, 杨日杰, 安昕, 等. 潜艇机动规避对抗吊放声纳搜索技术仿真研究[J]. 测试技术学报, 2009, 23(1): 14-18. Gao Xue-qiang, Yang Ri-jie, An Xin, et al. Simulation Research on Submarine Evasion to Fight Against Dipped Sonar Searching[J]. Journal of Test and Measurement Technology, 2009, 23(1): 14-18.
[3] 高学强, 杨日杰. 潜艇辐射噪声声源级经验公式修正[J]. 声学与电子工程, 2007(3): 17-18.
[4] 李凡, 郭圣明, 王鲁军, 等. 一种新的声纳作用距离指标评估方法[J]. 声学技术, 2009, 28(3): 235-239. Li Fan, Guo Sheng-ming, Wang Lu-jun, et al. A New Approach to Prediction of Sonar Detection Range Index[J], Acoustic Technology, 2009, 28(3): 235-239.
[5] Hardin R H, Tappert F D. Application of the Split-step Fourier Method to Numerical Solution of Nonlinear and Variable Coefficient Wave Equations[J]. SIAM Review, 1973(15): 423.
[6] Lee D, Pierce A D, Shang E C. Parabolic Equation Development in the Twentieth Century[J]. Journal of Computational Acoustics, 2000, 8(4): 527-639.
[7] Smith K B, Tappert F D. UMPE: The University of Miami Parabolic Equation Model Version 1.0[R]. MPL Technical Memorandum, 1993: 432.
[8] Collins M D. FEPE Users′ Guide[R]. Mississippi: Naval Ocean Research and Development Activity Stennis Space Center, 1988.
[9] Collins M D. A Split-step Pade Solution for the Parabolic Equation Method[J], Journal of the Acoustical Society of America, 1993, 93(4): 1736-1742.
[10] Michael D, Collins. Comparison of Algorithms for Solving Parabolic Wave Equations[J]. Journal of the Acoustical Society of America, 1996, 100(1): 178-182.
Operational Strategy for Helicopter with Dipping Sonar to Search Submarine
NI Chun-guang, CHEN Ying-chun, WANG Xian-hua
(Science and Technology on Underwater Acoustic Antagonizing Laboratory, Zhanjiang 524022, China)
The operational strategy for a helicopter with dipping sonar to search submarines under sea environment of thermocline is studied. The movement models of the helicopter and submarine are established, followed with the detection model of dipping sonar and the model of acoustic propagation model. The later considers the influences of sound velocity profile and sea bottom parameters. The influences of time delay of a helicopter, mission time of a helicopter, and merit factor of dipping sonar on the effectiveness of anti-submarine are analyzed based on Monte Carlo simulation, and the quantitative analysis result are given.
helicopter; dipping sonar; submarine; operational strategy
TJ67
A
1673-1948(2012)04-0317-04
2013-04-15;
2013-06-15.
水声对抗技术重点实验室基金资助项目(2011ssdkzd03.02).
倪春光(1968-), 男, 工程师, 研究方向为水声对抗技术.
(责任编辑: 许 妍)
