一种水下航行体附加质量数值计算方法

周景军, 李育英, 项庆睿



一种水下航行体附加质量数值计算方法

周景军, 李育英, 项庆睿

(中国船舶重工集团公司 第705研究所, 陕西 西安, 710075)

基于相对运动思想, 通过求解3D N-S方程, 给出了一种水下航行体附加质量高精度、高效的计算方法,可方便给出任意几何外形航行体的附加质量。该方法中, 水下航行体的附加惯性力(力矩)通过非定常运动与定常运动流体动力之差获得, 进而获得附加质量。通过在动量方程添加源项求解航行体非定常运动流场, 一方面保证能够模拟真实流场结构, 另一方面避免采用动网格过程中由于复杂网格重生带来的困难, 同时由于只采用了一套网格, 计算精度得到进一步保证。本文计算方法的精度通过椭球精确解得到有效验证, 具有重要的工程应用价值。

水下航行体; 附加质量; 数值计算方法; 相对运动

0 引言

物体在静止的流体中开始运动时, 必然会推动周围的流体质点, 使其克服惯性后也开始运动, 物体本身同时又受到这些流体质点的反作用力。流体中的物体在改变运动状态时, 为了克服流体惯性而受到的作用力称为惯性阻力。附加质量就是物体在流场中运动时流场惯性的一种度量。水下航行体的附加质量严重影响其运动特性, 是航行体操稳性分析、控制规律设计以及弹道预报的重要参数。目前, 计算附加质量的主要方法为基于势流理论的数值分析方法[1-2], 其关键是确定物体的速度势, 至今只有简单的球、椭球等形状物体能够获得理论精确解。工程上计算鱼雷等细长回转体的附加质量常用二元切片理论, 将雷体的附加质量看作是各横截剖面附加质量叠加之和, 并用修正系数考虑三元影响[3]。采用试验方法无疑更具可靠性, 但相比计算而言明显周期长、费用高, 对于某些复杂航行体而言, 同样存在着极高的难度。随着计算机能力的不断提高, 采用计算流体力学(computational fluid dynamics, CFD)数值仿真方法计算附加质量逐渐成为一种新的趋势, 国内已有多篇文章相继发表[4-6], 研究方法均是采用了动网格技术。尽管动网格技术更加接近实际流动, 但是对于具有复杂外形的航行体(例如带有泵喷、导管对转桨的鱼雷), 采用动网格技术难度较大, 难以保证网格重生的质量, 上述方法适用对象必然受限。

针对上述问题, 本文采用相对运动的思想, 通过施加合适的边界条件及在动量方程右侧添加源项的方法, 发展了一种新的附加质量CFD计算方法, 避免了动网格带来的一系列问题。通过采用椭球理论解的验证, 本文的数值方法计算效率高, 精度完全可以满足工程需求, 对于任意外形水下航行体均适用, 同时还给出了计算过程中一些特殊情况的处理方法。

1 附加质量的求解思路

附加质量的大小一般仅取决于流场中物体的形状及运动方向, 而与运动速度无关。附加惯性力的影响只有通过非定常运动才能有所表现。具体求解思路如下。

1.1 水下航行体非定常运动流场仿真

水下航行体加速直线运动、转动等非定常运动过程的数值仿真最直接的方法是采用动网格技术, 对于带有泵喷推进器、对转桨的水下航行体, 采用动网格技术由于涉及到网格重生, 网格质量难以保证, 从而严重影响求解精度。针对上述问题, 本文提出的求解方法, 网格只需要一次生成, 通过在动量方程中添加源项的方法, 保证了整个流场压力分布的真实性, 同时由于采用了相同的网格, 可以将网格的影响降到最低。

源项法以航行体纵向加速为例, 添加源项后方向的动量方程如下。

通过添加源项, 可以使流域前后压力场与实际流动情况一致, 避免产生压力差。

1.2 附加惯性力(力矩)计算

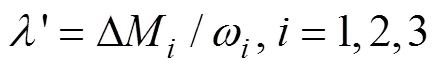
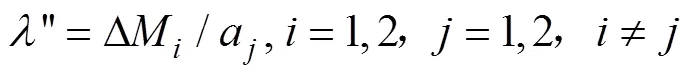
2 数值方法及计算模型

2.1 数值方法

本文数值方法采用基于求解3D N-S方程的有限体积法, 空间离散采用2阶迎风格式, 时间离散采用2阶欧拉后差格式, 采用多重网格技术加速收敛。湍流模型采用SST模型。

2.2 研究对象及网格验证

为了充分说明本文数值方法的有效性, 本文的计算模型选择了具有精确解的椭球体。如图1所示。椭球长半轴长40 cm, 短半轴长10 cm。建立了2套网格, 分别为单元数200万的结构化网格, 用于粘性流计算和单元数60万的非结构化网格用于无粘流计算。

图1 椭球体及其坐标定义

结构化网格计算结果如图2所示。椭球阻力系数理论解层流状态为0.20, 湍流状态为0.06。可以看出, 本文基于粘性流的数值方法和计算网格在预测椭球阻力系数时, 具有很高的精度, 下面给出附加质量的计算结果, 计算网格保持不变。

2.3 边界条件设置

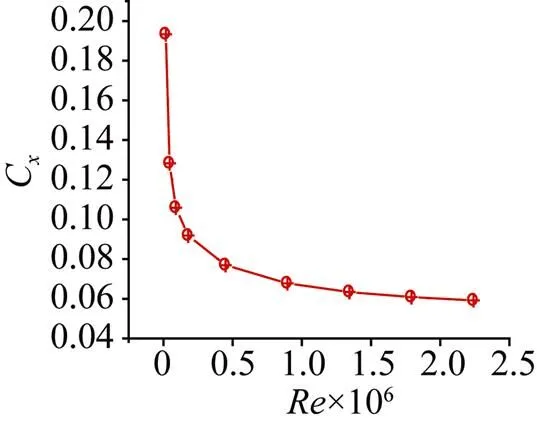
图2 不同雷诺数下的阻力系数

图3 加速过程压力场分布

图4 旋转域速度矢量和压力分布

Fig. 4 Pressure and velocity vector distributions in rotating field

3 附加质量特殊处理方法

图5 恒定速度下x方向阻力计算结果

另外, 对于形状复杂的航行体, 采用结构化网格难度很大。由于航行体的附加质量与流体粘性关系不大, 因此, 可以不求解边界层, 网格可直接采用非结构化网格, 即上述第2套网格。

4 计算结果

表1给出了椭球体附加质量理论解[8], 与表1相比, 表2所示的计算结果采用粘性流和理想流, 2种计算方法均可获得较好的计算结果, 误差均在5%以内, 说明附加质量基本和流体粘性无关。采用结构化网格(如图7所示)和非结构化网格差别不大, 非结构化网格适用于所有几何外形, 因此大大增加了本文计算方法的适用范围。

表1 椭球附加质量理论解

表2 附加质量理论解及计算结果

5 工程应用

图6 水下航行体几何外形

图7 计算网格

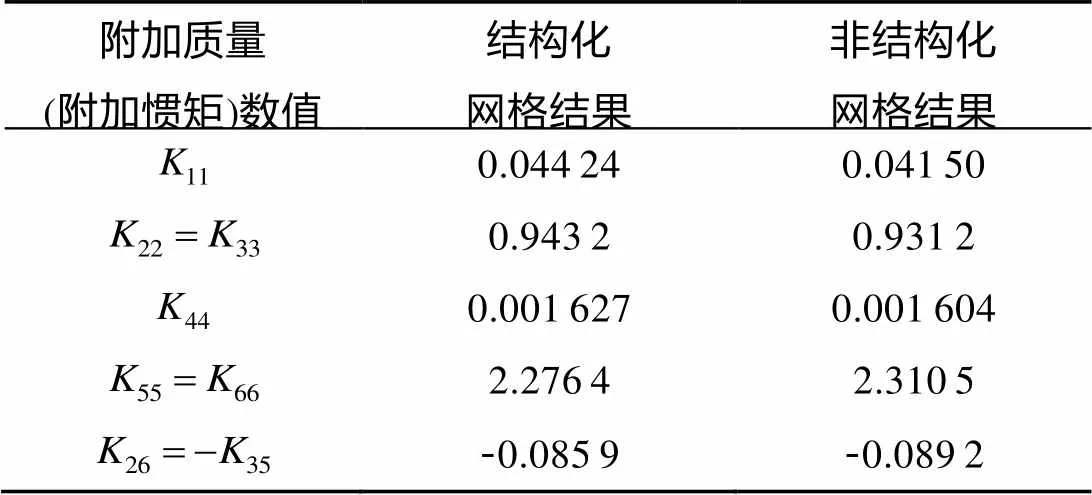
表3 附加质量计算结果

6 结束语

本文基于相对运动思想, 提出了一种附加质量的CFD快速计算方法, 避免了采用动网格带来的一系列问题, 由于该方法可直接采用非结构化网格, 因此适用于任意复杂的几何外形, 大大增大了该方法的适用范围, 具有一定的工程应用价值。

[1] 刘丹, 王晓亮, 单雪雄. 平流层飞艇的附加质量及其对飞艇运动的影响[J]. 计算机仿真, 2006, 23(6): 52-56. Liu Dan, Wang Xiao-liang, Shan Xue-xiong. Added Mass to Stratospheric Airship and Its Effect on Motion[J]. Computer Simulation, 2006, 23(6): 52-56.

[2] 林超友, 朱军. 潜艇近海底航行附加质量数值计算[J]. 船舶工程, 2003, 25(1): 26-29. Lin Chao-you, Zhu Jun. Numerical Computation of Added Mass of Submarine Maneuvering with Small Clearance to Sea-bottom[J]. Ship Engineering, 2003, 25(1): 26-29.

[3] 张向强, 姜鲁华, 王生, 等. 飞艇动力学仿真[J]. 计算机仿真, 2008, 25(6): 79-82. Zhang Xiang-qiang, Jiang Lu-hua, Wang Sheng, et al. Dynamic Equations of Airship[J]. Computer Simulation, 2008, 25(6): 79-82.

[4] 马烨, 单雪雄. 数值计算复杂外形物体附加质量的新方法[J]. 计算机仿真, 2007, 24(5): 75-78. Ma Ye, Shan Xue-xiong. A New Numerical Computation Method for Added Masses of Complicated Object[J]. Com- puter Simulation, 2007, 24(5): 75-78.

[5] 傅慧萍, 李杰. 附加质量CFD计算方法研究[J]. 哈尔滨工程大学学报, 2011, 32(2): 148-152. Fu Hui-ping, Li Jie. Numerical Studies of Added Mass Based on the CFD Method[J]. Journal of Harbin Engineering Uni- versity, 2011, 32(2): 148-152.

[6] 弓三伟, 陆宏志, 邹正平, 等. 弹性体和带空泡体的附加质量动态数值计算[J]. 计算机仿真, 2010, 27(4): 349-353. Gong San-wei, Lu Hong-zhi, Zou Zheng-ping, et al. Hydro- dynamic Numerical Computation of the Added Mass of Elastic Body & Cavitation Bubble[J]. Computer Simulation, 2010, 27(4): 349-353.

[7] 吴望一. 流体力学[M]. 北京: 北京大学出版社, 2000: 154-166.

[8] 张宇文. 鱼雷外形设计[M]. 西安: 西北工业大学出版社, 1998: 713-716.

A Numerical Computation Method of Additional Mass for Underwater Vehicle

ZHOU Jing-jun, LI Yu-ying, XIANG Qing-rui

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China )

A high-precision and high-efficiency method of computing additional mass for an underwater vehicle is proposed by solving the 3-D N-S equations based on the relative motion principle. This method is convenient to compute the additional mass for an underwater vehicle with complex shapes. The additional inertia force(moment) is achieved from the difference of hydrodynamics of fluids in unsteady and steady motions, then the additional mass is obtained. By adding the source term to the momentum equation, the unsteady flow field is solved to simulate the real structure of flow field, and the difficulty generated by complex grid rebirth in using the dynamic grid is avoided. The accuracy of the proposed method is also assured because of adopting the same grid. The validity of the proposed method is verified by the exact solution of ellipsoid.

underwater vehicle; additional mass; numerical computation method; relative motion

TJ630.2; TV131

A

1673-1948(2013)04-0246-04

2012-10-18;

2013-03-21.

中国博士后科学基金特别资助(2013T60895).

周景军(1981-), 男, 博士, 主要研究方向为鱼雷总体技术.

(责任编辑: 陈 曦)