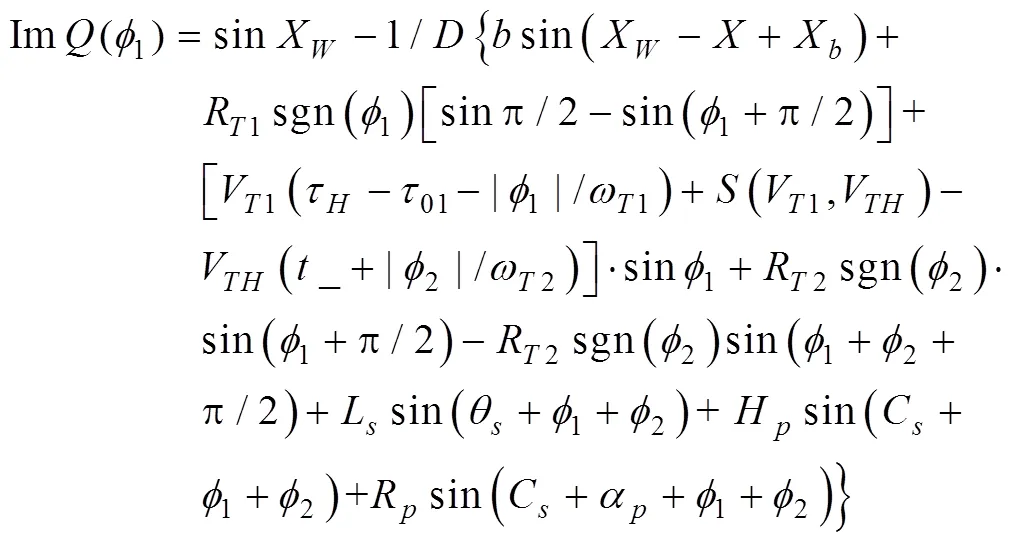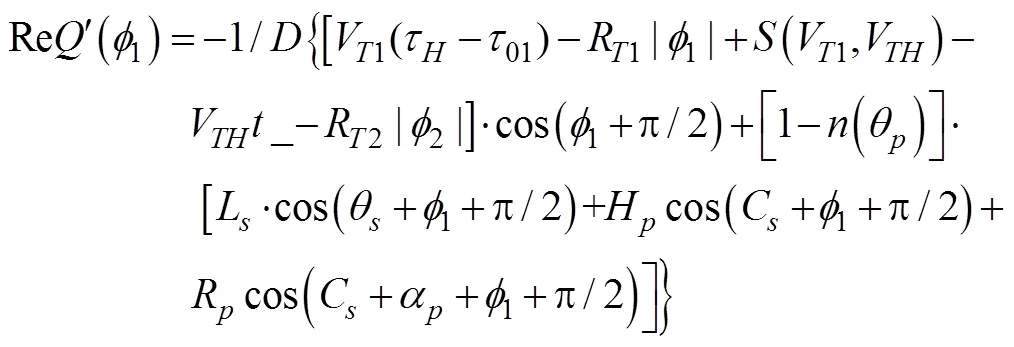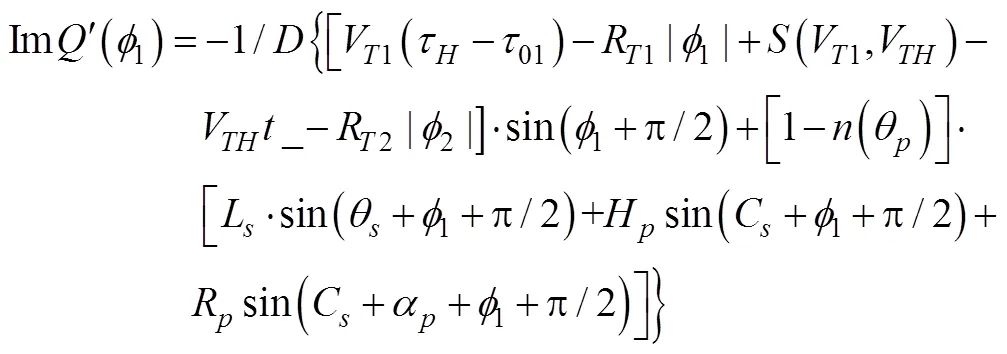预定相遇态势的鱼雷二次转角射击通用模型与算法
2013-05-28李长文李本昌
李长文, 李本昌, 初 磊
预定相遇态势的鱼雷二次转角射击通用模型与算法
李长文, 李本昌, 初 磊
(海军潜艇学院 科研部, 山东 青岛, 266042)
为了解决预定相遇态势二次转角射击参数的计算问题, 考虑鱼雷可能的变速及特殊弹道过程, 建立了可满足不同射击方式需求的通用数学模型, 给出了牛顿迭代算法的相关公式。用数值实验的方法对模型及算法的正确性进行了验证, 结论表明模型及算法可满足直航、声自导、尾流自导、齐射、目标选择等射击参数计算的需求。
鱼雷; 预定相遇态势; 二次转角; 射击参数
0 引言
对于非线导雷射击, 鱼雷射击的目的实际上应为满足特定的命中态势, 所谓命中态势即假设无误差条件下与鱼雷固连的遮盖中心及与目标固连的瞄准点相遇时刻的态势。当对命中角不作要求时, 可以用一次转角射击实现, 若对命中角有要求, 一般必须采用二次转角射击实现。
对鱼雷命中角有要求的情形包括: 尾流自导的进入角、有利于声自导探测的命中角、攻击舷别与目标舷别不同的情形等。当考虑预设命中角时, 同时还必需考虑鱼雷完成二次转角及自导开机等特殊弹道至遮盖中心与瞄准点(假设无误差无自导条件下)相遇的直航距离, 以满足搜索弹道的目标选取及遮盖可能的误差等需要, 所谓预定相遇态势就是指规定命中角以及这个距离。
关于预定相遇态势的二次转角射击的意义和作用, 参见文献[1]。本文将就这一问题进行抽象, 试图建立一个通用模型, 并研究求解的算法。
1 二次转角射击输入输出参数及描述模型
1.1 目标及瞄准点
舰艇为一个有一定长度L的运动目标, 规定其参考坐标系原点O为舰艉,x轴正方向为艉艏线方向,y轴正方向为舰艇在水平面上的正右方向,z轴正方向为竖直向下方向。瞄准点是与这个运动的参考系固连的一个点, 对于只考虑水平面上运动的情形,点位于xOy面上, 其对应的复数为
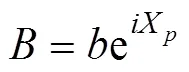
式中:为瞄准点到舰艉的距离;X为瞄准点在水平面上关于目标的舷角;X= 0或p对应的瞄准点位于目标正前方或正后方。对于声自导鱼雷射击, 通常取= 0,X的取值无影响, 对于直航鱼雷通常取= 0.5L,X= 0, 对于尾流自导鱼雷射击, 通常取= 0.5(Vt–L),X=p,t为尾流持续时间。
1.2 遮盖中心
鱼雷为一个有一定长度的运动目标, 规定其参考坐标系原点O为前端点,x轴正方向为艉艏线方向,y轴正方向为鱼雷在水平面上的正右方向,z轴正方向为竖直向下方向。遮盖中心是与这个运动的参考系固连的一个点, 其作用为, 进行射击参数计算时, 在假设无误差无自导条件下, 遮盖中心将与瞄准点相遇。对于只考虑水平面上运动的情形,点位于xOy面上, 对应的复数为
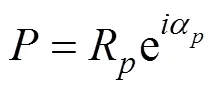
式中:R为遮盖中心到鱼雷的距离;为遮盖中心相对鱼雷的舷角。对于声自导鱼雷, 若取半径为半顶角为的声自导扇面的形心为遮盖中心, 则R= 2sin/ ( 3),= 0。对于直航或尾流自导鱼雷, 遮盖中心即鱼雷, 相当于R= 0。
1.3 射击态势
所谓射击态势是指潜艇采用目标运动要素时刻(称为0时刻)潜艇位置点与目标位置点构成的相对态势。潜艇位置点为对目标的观测站, 这个点到鱼雷出管位置点的距离以0表示, 假设潜艇发射鱼雷前作等速直航运动, 其设定(速率, 航向)以(,)表示, 真实速率(速率, 航向)以(0,0)表示。
目标位置点为目标舰艉, 0时刻的目标运动要素以(方位, 距离, 速率, 航向)表示。目标运动要素有真值与观测值之分, 真值是客观存在的, 基于真值进行仿真研究, 所得结论是客观的, 即可用重复试验的方法进行验证的, 因此可用于鱼雷效能评估。目标运动要素观测值一般是由纯方位等方法解算的, 一定条件下可以看成真值、系统误差、随机误差通过特定系统的输出, 目标运动要素观测值是鱼雷射击现场决策的起点, 主要用于计算射击参数, 分别以(0,0,0,0)和(,,,)表示目标(方位, 距离, 速率, 航向)真值和观测值。
目标距离是指目标方位线上的距离, 目标方位有实际方位与可观测方位之分, 可观测方位是指由观测设备给出的目标声信号的到达方位, 由于声速有限的延迟作用, 可观测方位不等于实际方位, 其差异程度与目标声源到观测站的距离密切相关, 若采用目标运动要素时刻的方位取当前时刻的可观测方位, 则应考虑声速的作用, 假设声音传播相当于速率V的匀速直线运动, 则无误差条件下0时刻目标实际位置点为O=e+(/V)e。由于目标运动要素一般是通过对目标的观测解算的, 解算过程中可以假设作为运动要素的目标方位和距离为实际方位和距离, 因此, 可以不再考虑声速的作用, 无误差条件下0时刻的目标实际位置点为O=e, 下面将运用这一假设。
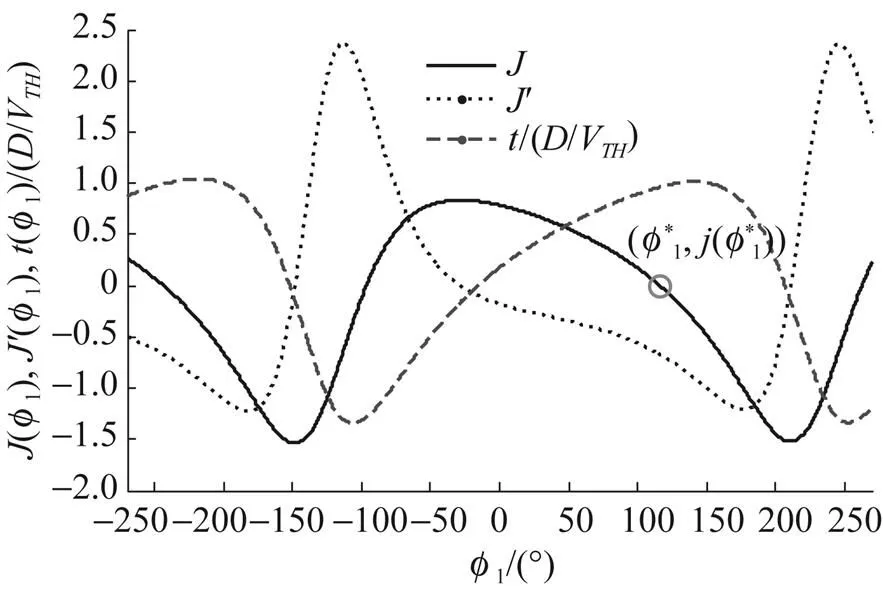
用于射击参数计算的决定发射鱼雷时刻潜艇与目标的相对态势还可以用潜艇相对目标的距离观测值、速率观测值、舷角观测值、潜艇速率设定值以及目标相对潜艇舷角设定值X表示, 这时, 给定目标方位对应的目标航向、潜艇航向的观测值可表示为= rb(––p),= rb(–X)。rb()为自定义函数, 其作用为将角变为[–p,p) 上与终边相同的角, 计算公式为: 若 mod(, 2p) 为达成发射鱼雷的目的, 需要为鱼雷设计相应的弹道, 这就要考虑鱼雷的弹道逻辑。为便于表达, 此处不考虑鱼雷初始弹道可能的复杂变速、变深、以及特殊弹道在时空上的作用, 下面的假设只是用于说明一些方法的学术研究, 不能用于实际目的。 假设鱼雷出管后在水平面上投影点的运动为直线或圆周运动, 自0时刻至鱼雷出管的时间以0表示, 鱼雷出管后经时间01完成一些变速变深等运动, 速率稳定于V1, 在水平面上航行的距离为, 之后以角速率1执行水平面上的一次转角1的匀速圆周运动, 转角运动结束后直航, 至初次变速时刻进行V1到V的变速, 初次变速时刻以鱼雷出管后的时间表达,的设定值应与初次变速前的鱼雷弹道逻辑相容, 假设变速运动在水平面上为直线运动, 变速时间为(V1,V)、水平面上航行的距离为(V1,V), 变速运动完成后鱼雷以速率V进行水平面上的等速直航。至二次转角时刻以角速率2执行二次转角2的匀速圆周运动, 二次转角完成后执行一些规定的特殊弹道, 完成这个特殊弹道所用时间以表示,= 0表示无特殊弹道。对于> 0的情形, 特殊弹道完成后鱼雷在水平面上前进的距离、位置点偏离原航向的角、航向偏离原航向的角、航速以L,,C,V表示。 一次转角射击即二次转角等于0的二次转角射击。无论一次转角射击或二次转角射击, 总假设鱼雷完成特殊弹道后直航距离H, 遮盖中心与瞄准点满足无误差的相遇条件,H≥0 为一个预设定参数。射击参数的计算是为了达到无误差条件下使遮盖中心与瞄准点相遇的目的, 相遇时刻鱼雷航向的反方向相对目标航向的角称为命中角。 若给定相遇态势, 以表示预定命中角, 一般只能用二次转角射击实现。若不给定相遇态势, 以=Æ表示, 可用一次转角射击实现遮盖中心与瞄准点的相遇, 无误差条件下的命中角由射击态势及鱼雷弹道逻辑决定。 2为1,的函数, 若不限制二次转角范围, 则可取 此函数关于1连续可导, 且¢2(1) = –(), 其中 二次转角射击参数计算的输出参数主要有一次转角1、二次转角2、二次转角时刻2或对应的鱼雷航程、执行特殊弹道时刻t或对应的鱼雷航程、特殊弹道结束时刻t¢或对应的鱼雷航程、无误差及自导运动假设下遮盖中心与瞄准点相遇时刻以及鱼雷到达目标航向线的时刻t或鱼雷航程等。输入参数有: 1) 射击态势(,,,,X)、发射延迟0; 2) 潜艇观测站到鱼雷出管位置点的距离0、鱼雷弹道参数V1,1,,1,(V1,V),(V1,V),V,2,,L,,C,V; 3) 瞄准点(,X)、遮盖中心(R,)、预定相遇态势(,H)。 假设无误差条件下0时刻发射的鱼雷于时刻到达位置点(), 同时遮盖中心与瞄准点以预定相遇态势相遇。根据前面的论述, 二次转角射击参数计算的关键是建立确定 (1,)的方程。 如图1,时刻目标及瞄准点为 O() =e+e(5) 鱼雷特殊弹道结束时刻为t¢=–H/V, 开始时刻即二次转角结束时刻为t=t¢–, 二次转角运动开始时刻为 2=t– |2|/2=–H/V–– |2|/2(7) 1= (0+0+)e(8) 式中:R1=V1/1。鱼雷V1®V变速开始时刻为t=0+, 结束时刻为t¢=t+(V1,V), 相应的鱼雷位置点为 自t¢开始, 鱼雷以速率V直航, 至2时刻开始二次转角, 于2¢时刻完成二次转角运动, 时刻应满足2–t¢=–_– |2|/2≥0, 其中 _=0++(V1,V) ++H/V(12) 在这一条件下,2,2¢时刻鱼雷位置点为 其中,R2=V/2。t时刻鱼雷位置点为 时刻鱼雷位置点()遮盖中心为 =对应的方程为 上式两边同除以e, 利用X与-、-与X--p为终边相同的角, 以及esgn(x)p/2= sgn(), 可得 此为确定(1,)的方程, 时刻还应满足条件 若满足这些关系的(1,)一般不唯一, 应取值最小的那一组(*1,*)作为射击参数。 记 则前面确定(1,)的方程即 = (/V)[(1) /(1)] (23) 以Im、Re表示复数的虚部、实部, 因为为实数, 所以= (/V)Re((1)/(1)), 且 Im((1)/(1)) = 0 (24) 此为一次转角1所满足的方程。若限制1Î(–3p/2, 3p/2 ), 则(*1,*)为 min= (/V)Re[(1)/(1)] s.t.(1)≥_+ |2(1) | /2 (1) = Im[(1) /(1)] 1Î(– 3p/2, 3p/2) (25) 的解, 射击参数存在的条件为*<¥, 这就是给定相遇态势的二次转角射击参数模型。 函数(1)在 (–3p/2, 3p/2)内一般有3个0点, 满足要求的不超过2个, 一般只有1个, 因此解这个优化问题的关键是解方程(1) = 0。 式中, 起点11可取[,]的左或右端点, 迭代结束条件为|1n|≥3p/2, 或|(1n)|≤, 或≥N, 对于= 10– 15的情形, 可取最大迭代次数N= 10。 函数(1)导数的计算公式为 函数(1)的公式中符号函数及绝对值函数的导数以其广义导数表示, 即sgn¢() = 2(), ||¢= sgn(),()为Dirac-函数。则 利用这些公式可以实现¢(1)的计算。 若1= 0, 则鱼雷出管后不进行一次转角, 可称为直进射击, 射击方向为潜艇航向, 这个航向相对采用目标运动要素时刻目标方位线的角= rb(–) = –X称为直进射击的提前角。 对于不预设相遇态势的情形,2= 0, 鱼雷发射后将一直直航。在前面的公式中令1=2= 0,X= –, 可得 记 则 所以 式中,满足方程|(V/)+|2= |– (/)|2, 即 即不预设相遇态势的直进射击提前角及相遇时刻可用上述解析公式计算。 为验证以上公式及算法的正确性, 对于用以上方式计算的射击参数, 可以用动画形式显示各时刻潜艇、鱼雷、目标的位置及航向, 关键是(*1)时刻遮盖中心与瞄准点是否重合且满足预定相遇态势。下面设定一个特殊弹道用于测试, 假设自t时刻开始, 鱼雷以速率V直航l, 之后直航变速至V, 变速运动的时间为(V,V), 航程为(V,V), 之后以角速率转向, 转向运动完成后直航l, 然后转以角速率转向, 转向运动完成后直航l。 数值实验发现, 以上这些公式及算法是正确的, 考虑到(1)/(/V) 与(1)有相同的符号与极值点, 且(1),¢(1),(1)/(/V)是无量纲的, 为便于直观理解求解1*的算法, 可以将它们的图像画在以1为横坐标(单位为度)纵坐标无量纲的一个直角坐标系内, 其典型图像见图2。 图3为另一次实验的至*时刻的鱼雷弹道平面图, 输入参数为:=19kn,= 50°,= 50 cab,0= 2 s,X= 50°,= 5 kn,0= 25 m,= 100 m,= 20 s,V1= 25 kn,1= 10°/s,1= 15°/s,l=l=l= 500 m,= – 50°,= 100°,=15°/s,V= 50 kn,= 1000 m,X= –90°,R= 938.9574 m,= –45°,H= 1000 m,= –150°, 假设鱼雷的变速运动为加速率0.5 m/s2的匀变速直线运动。计算的射击参数为1*= 62.7804°,2*= 91.2196°,*= 515.5107 s。画图所用初始方位= 0, 这些参数的选取只是为了验证公式及算法, 并非出于实用的目的。改变相关参数, 可以产生比较复杂的态势。 图2 计算射击参数的图像 图3 鱼雷弹道平面图 两雷平行航向齐射的目的是实现无误差条件下鱼雷二次转角完成后的航向线平行且各雷分别命中“目标”的舰艏及舰艉, 所谓“目标”是指一段抽象的区域, 其长度为目标或目标及其尾流长度的一定倍数。在不考虑鱼雷变速、变向、变深等条件下, 有一组传统的计算两雷一、二次转角等射击参数的公式, 文献[2]指出, 这些公式计算的射击参数不能实现无误差条件下各雷分别命中舰艏及舰艉的设想[3-6]。考虑鱼雷可能的变速、变向、变深等弹道过程, 必须重新设计两雷平行航向齐射参数的计算方法。 平行航向齐射的实质是预先设定命中角的二次转角射击, 这个预先设定的命中角就是假想的中线鱼雷一次转角射击的命中角, 将两雷齐射看成两次预定相同命中角的单雷射击, 选择两条鱼雷的瞄准点分别为目标舰艏及舰艉, 利用前面的方法计算射击对数, 就可实现平行航向齐射的目的。假想的中线鱼雷的射击瞄准点及发射延迟理论上可以随便选取, 一般可选择目标中点作为其瞄准点, 2条鱼雷发射时刻的中间时刻作为其发射时刻。 以上将潜艇鱼雷转角射击在一般意义下进行了抽象的研究, 其目的是建立一个通用模型, 使其适用于不同射击或攻击方式的需求。为此对瞄准点、遮盖中心、预定相遇态势、特殊弹道等进行了一般的参数化描述, 这些参数的特定取值可对应于传统的射击参数计算方法。 利用以上模型及算法可以很简单地编制一个动画实验程序, 对以上公式及算法进行验证。有目的的设置参数的不同取值, 可以就特定的攻击态势对所关心的问题进行直观地实验研究。 用复数表示平面上的向量或点, 使公式推导十分简洁, 不容易出错且易于检查, 还有利于编程实现。用支持复数运算的软件(Matlab等), 上述计算的编程很简单, 若用不支持复数运算但支持运算符重载的语言(VC++, VC#等)编程, 可先编写一个支持复数运算的类, 以实现复数的相关计算。若用不支持运算符重载的语言(Ja等)编程, 或不预先编写一个支持复数运算的类, 就需要将前面的公式改写成虚部及实部的分量形式。为便于检查, 这些公式中复数的实部只用余弦, 虚部只用正弦。 (1),(1)的分量形式可以很方便地给出。 Re(1) = cos1+ (/V)cos(X–) (38) Im(1) = sin1+ (/V)sin(X–) (39) ¢(1)的分量形式为 利用分量形式, 复数的辐角及大小可用arg= atan2(Im, Re), || = [(Im)2+ (Re)2]1/2计算, 复数相乘及相除对应的复数的虚部及实部可借助于辐角进行, 其公式为 Im(12) = |1||2|sin(arg1+ arg2) (42) Re(12) = |1||2|cos(arg1+ arg2) (43) Im(1/2) = |1||2|sin(arg1– arg2) (44) Re(1/2) = |1||2|cos(arg1–arg2) (45) [1] 李本昌, 李长文. 预定相遇态势的潜射鱼雷射击及其技术方法[J]. 指挥控制与仿真, 2013, 35(2): 5-8.Li Ben-chang, Li Chang-wen. Firing and Technical Method Based on Given Meeting Situation of Sub-laun- ched Torpedo[J]. Command Control & Simulation, 2013, 35(2): 5-8. [2] 李长文, 王鹏. 一种新的两雷平行航向齐射参数计算方法[J]. 潜艇学术研究, 2012, 30 (5): 46-48. [3] 夏佩伦, 刘勇, 陈志鹏. 直航鱼雷齐射命中间隔的计算与分析[J]. 鱼雷技术, 2010, 18(4): 308-311.Xia Pei-lun, Liu Yong, Chen Zhi-peng. Calculation and Analysis of Hit Spread for Straight Running Torpedo Salvo[J]. Torpedo Technology, 2010, 18(4): 308-311. [4] 李本昌, 梁涛. 尾流自导鱼雷的齐射及其建模[J]. 火力与指挥控制, 2008(6): 128-130. Li Ben-chang, Liang Tao. Method and Model on Salvo Launching Wake-guided Torpedoes[J]. Fire Control & Command Control, 2008(6): 128-130. [5] 赵正业. 潜艇火控原理[M]. 北京: 国防工业出版社, 2003. [6] 张静远. 鱼雷作战使用与作战能力分析[M]. 北京: 国防工业出版社, 2005. General Model and Algorithm of Two-time Turn Angle Shooting of Torpedo for Predetermined Encountering Situation LI Chang-wen, LI Ben-chang, CHU Lei (Office of Science Research Department, Navy Submarine Academy, Qingdao 266042, China) To compute the parameters of two-time turn angle shooting of a torpedo for predetermined encountering situation, a general model satisfying the requirements of different shooting modes is constructed by considering possible special trajectory and torpedo velocity change. The formulas for Newton iteration algorithm are given. The correctness of the proposed model and algorithm is validated by numerical experiment, and the results indicate that the model and algorithm can satisfy the computation requirements of the shooting parameters for straight running, acoustic homing, wake homing, salvo, target selection, etc. torpedo; predetermined encountering situation; two-time turn angle; shooting parameter TJ630 A 1673-1948(2012)04-0306-07 2013-04-25; 2013-05-11. 李长文(1962- ), 男, 副教授, 研究领域为军事运筹. (责任编辑: 许 妍)1.4 鱼雷弹道逻辑及参数假设
1.5 预定相遇态势

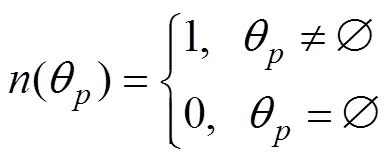
1.6 二次转角射击输入输出参数
1.7 二次转角射击的描述模型
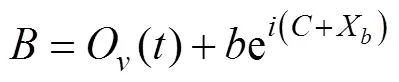

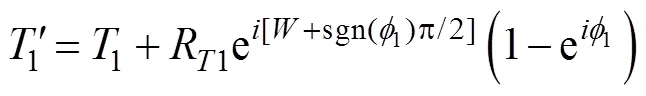
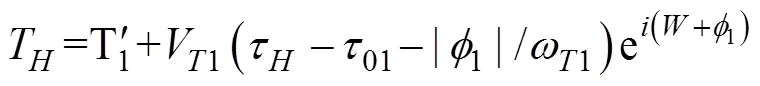

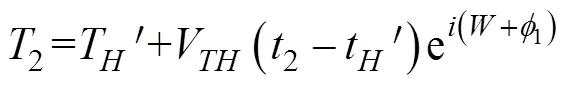

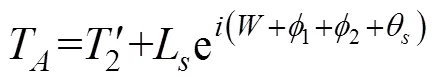
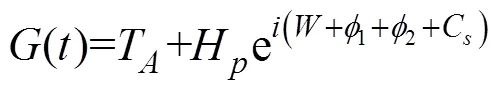

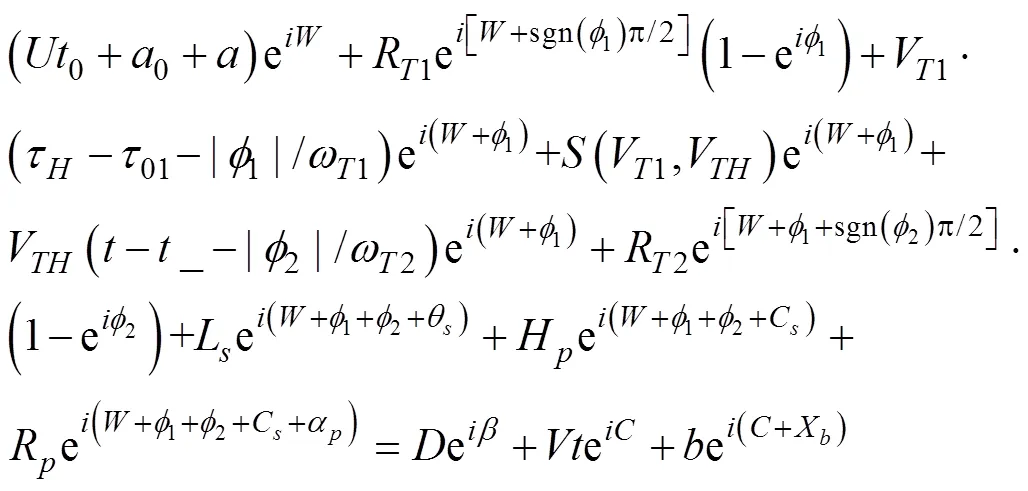
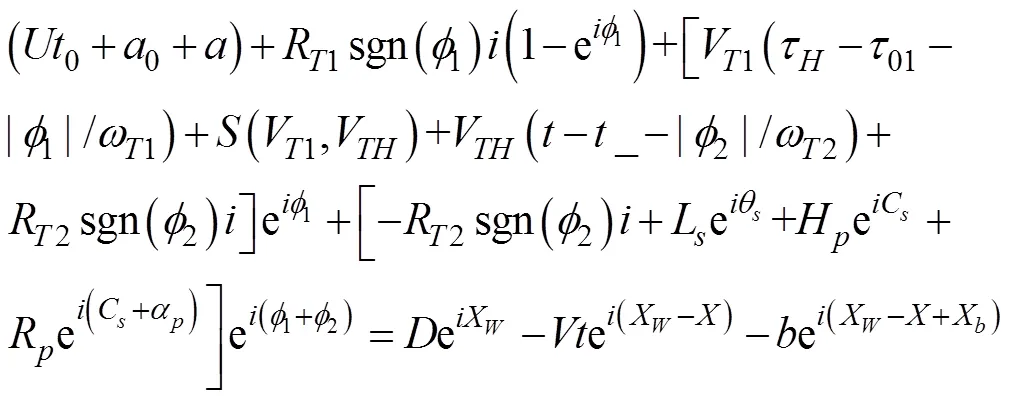
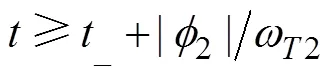

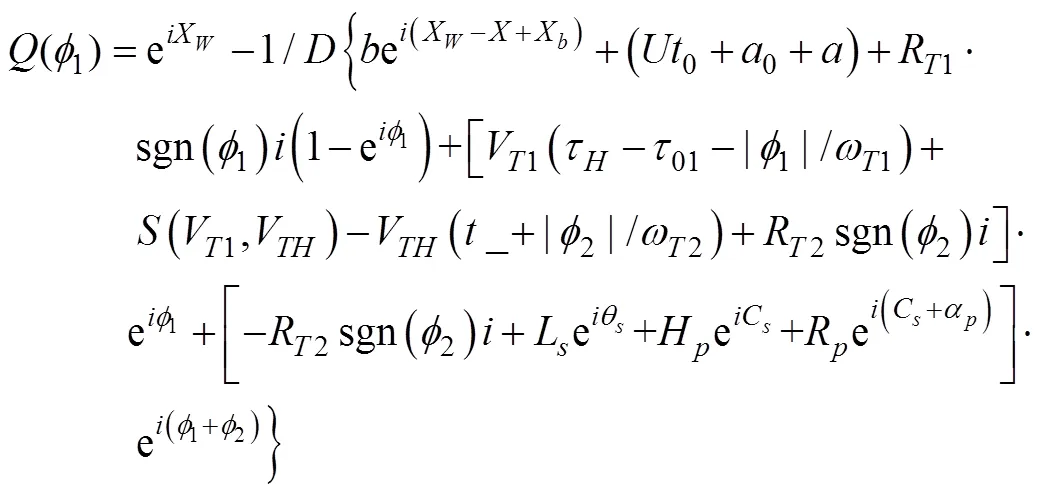
2 射击参数计算方法
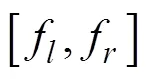
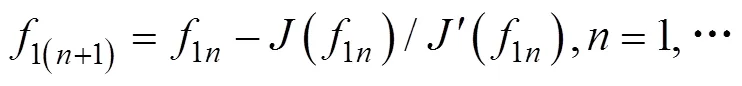
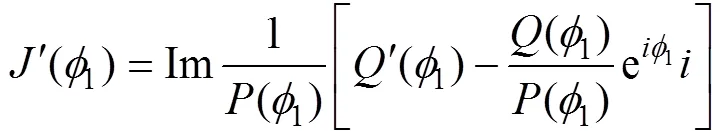
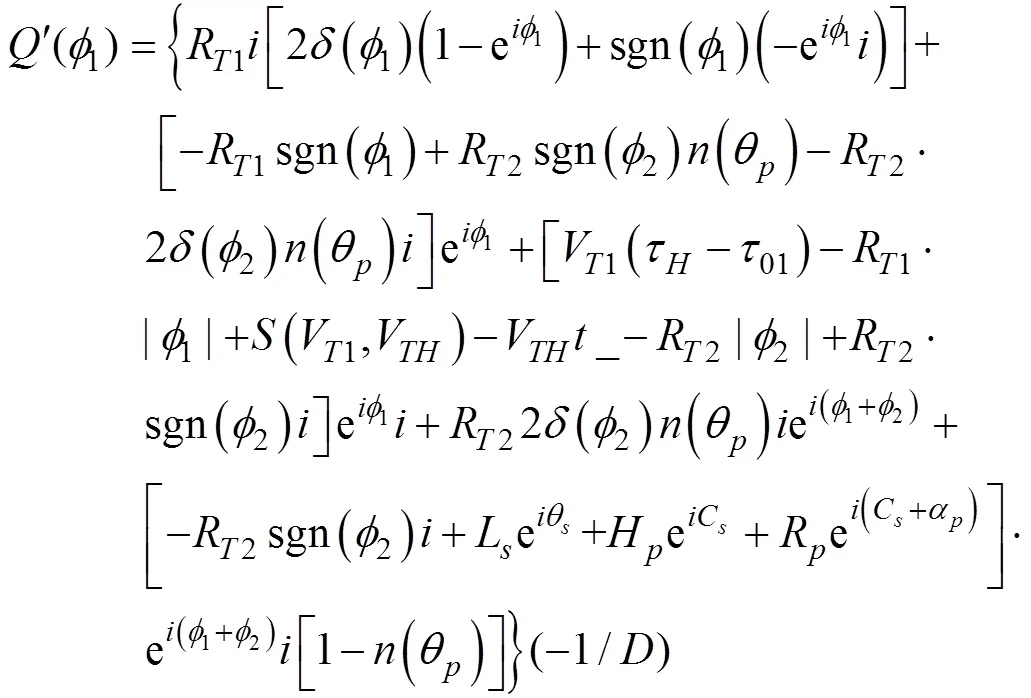
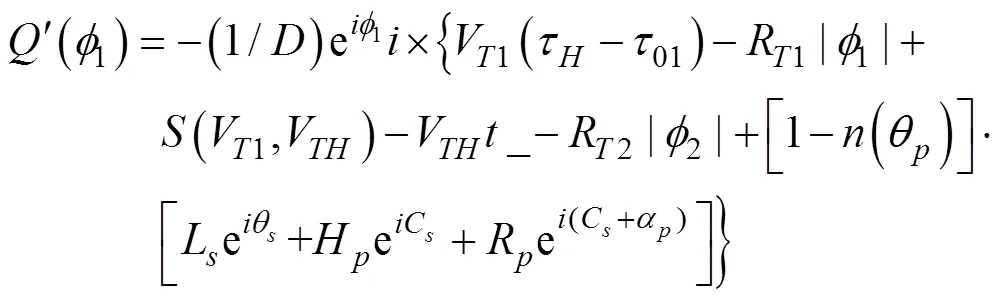
3 不预设相遇态势的直进射击提前角

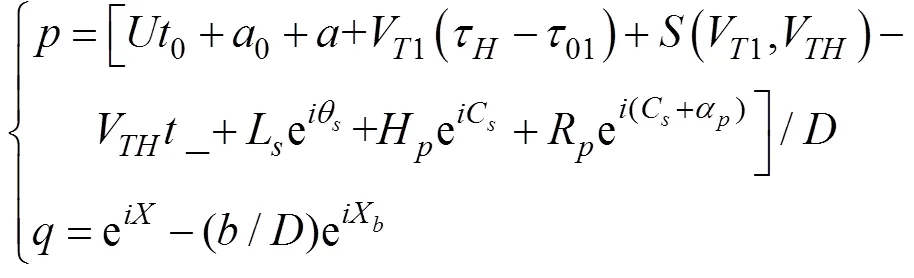

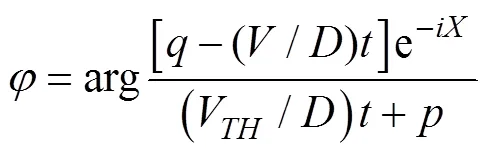

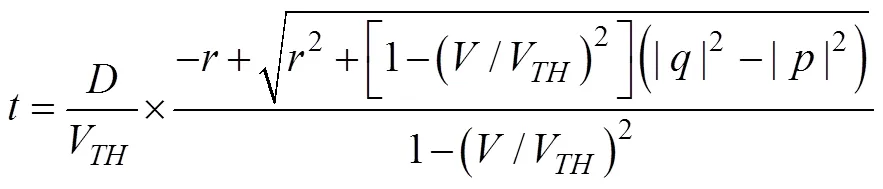
4 公式验证及算法实验

5 平行航向齐射参数的计算
6 结束语