基于等几何有限元法的功能梯度板自由振动分析
2013-05-24尹硕辉余天堂
尹硕辉,余天堂,刘 鹏
等几何有限元法是一种将CAD与CAE有机统一起来的新型有限元法[1],该方法采用CAD中样条基函数(如B样条、T样条、NURBS样条等)作为形函数,从而能形成“精确”的计算网格。与常规有限单元法相比,等几何有限元法具有高精度和高收敛率的优点。此外,常规有限单元法近似通常仅具有C0连续性,不能有效地求解高阶偏微分方程问题(如薄板壳等)。等几何有限元法可以构造任意高阶连续的基函数,能有效地求解高阶偏微分方程。等几何有限元法已成功地求解流体力学[2]、板壳分析[3]、电磁场[4]、相场[5]、拓扑优化[6]以及裂纹扩展[7-8]等问题。
功能梯度材料(FGM)是一种材料性质和功能呈梯度变化的新材料[9],使结构既具有良好的耐高温和抗腐蚀性能又具有较高的强度和韧性,因此在航空航天、核能、生物医学、机械、建筑等领域得到了广泛应用。功能梯度材料结构在工作状态下表现出复杂的力学行为。一些学者基于不同的板理论(如经典板理论[10]、一阶剪切变形板理论[11]和高阶板理论[12]等)和数值方法(如有限元法[11]、无网格法[13-14]和光滑有限元法[15-16]等)分析了功能梯度板的力学行为,得到了一些有益的结论。
本文针对金属-陶瓷功能梯度板,考虑板材料性能沿厚度方向呈梯度连续变化,基于一阶剪切变形板理论,推导了非均匀有理B样条(NURBS)等几何有限元基本公式;采用NURBS等几何有限元分析了梯度指数、边界条件及长厚比对功能梯度板自振频率的影响。
1 基于一阶剪切变形理论的功能梯度板的基本方程
图1所示为金属-陶瓷功能梯度非均匀材料板,其材料性质沿厚度方向呈现梯度变化。设从板的上表面到下表面,金属的体积分数从100%过渡到0%,陶瓷的体积分数则由0%到100%。
基于一阶剪切板理论[11],板内任意一点的位移为:
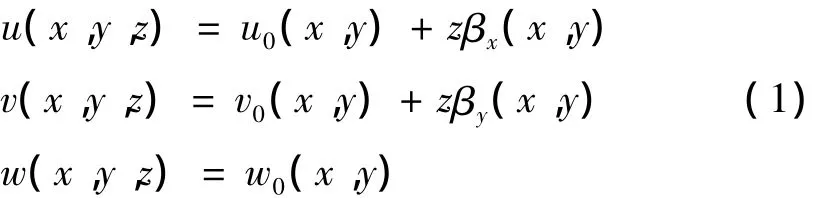
其中:u0、v0和 w0分别代表板中面某点的位移;βx、βy代表中面法线变形后在xz平面和yz平面上的转角。
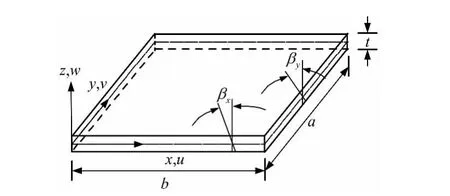
图1 金属-陶瓷功能梯度板示意图Fig.1 The graph of metal/ceramic FGM plate
平面内的应变为:

其中:εm和εb分别为中面面内应变场和板的曲率场,
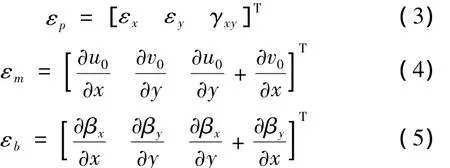
此外,板的横向剪应变场为:
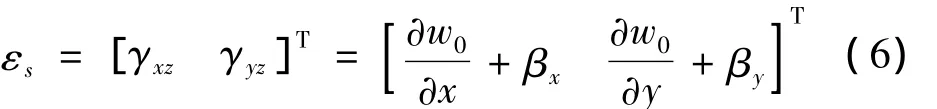
根据胡克定律,在正轴下板内的应力-应变关系可表示为:
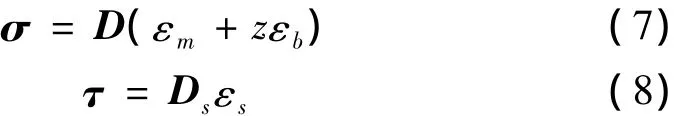
其中:σ=[σxσyτxy]T,τ=[τxzτyz]T分别为平面内应力及横向应力。弹性矩阵为:
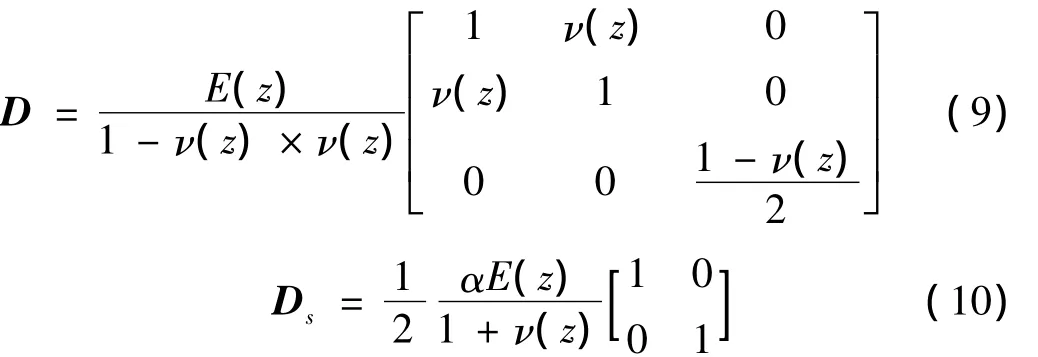
其中α为剪切修正因子(本文取5/6)。
弹性模量E、泊松比ν和物质密度ρ等物性参数是坐标 z的函数[14]:
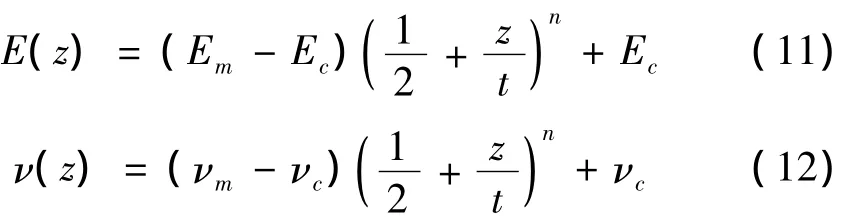
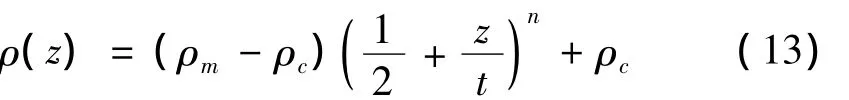
其中:n为梯度指数;下标c和m分别为陶瓷材料和金属材料;t为板厚。
2 等几何有限元法
2.1 节点矢量和B样条基函数
节点矢量 U={ξ1,ξ2,…,ξn+p+1}由一系列参数坐标点组成,其中 ξi为第 i个节点,ξi≤ξi+1,i=1,2,…,n+p+1,p为基函数的阶次,n为形成B样条曲线所需基函数数目(与控制节点数目相等)。当节点矢量中所有相邻节点间距相等(即ξi+1-ξi为常数),称之为均匀节点矢量,反之为不均匀节点矢量。当节点矢量两端点(ξ1,ξn+p+1)重复度为p+1时,称之为开式节点矢量。等几何有限元法通常使用开式节点矢量,不为零的节点区间定义为单元[ξi,ξi+1]。B样条基函数在节点区间[ξi,ξi+1]内具有无穷阶可导,在节点 ξi处具有Cp-k连续,k为节点重复出现的次数,称为重复度。给定节点矢量 U,B 样条基函数 Ni,p(ξ)定义为[17]:
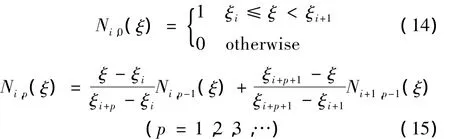
当B样条基函数阶次p=0和p=1时,等几何有限元法即为常规有限元法;当p≥2时,等几何有限元法不同于常规有限元法。
2.2 NURBS曲面
B样条曲线定义如下[17]:
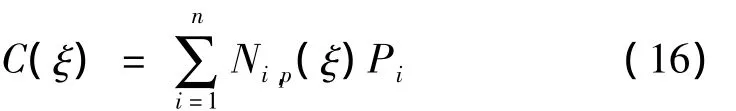
其中:Pi=(xiyizi)为第i个控制节点坐标,类似于常规有限元法的结点坐标;Ni,p(ξ)为定义在开式节点矢量上的p阶基函数。
给定n×m个控制节点Pij及ξi和ηj方向的节点矢量 U={ξ1,ξ2,…,ξn+p+1},V={η1,η2,…,ηm+q+1}。采用张量形式,二维B样条曲面定义为:
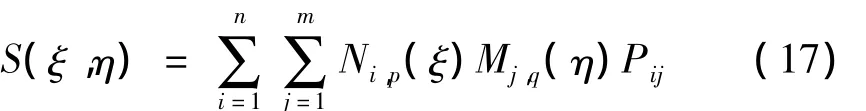
其中:Ni,p(ξ)、Mj,q(η)分别为 ξi和 ηj方向节点矢量 U和V上定义的B样条基函数。
在B样条曲面中对每个控制节点Pij乘以一个相应的权因子 ωij得到 NURBS样条曲面。权函数定义为[17]:
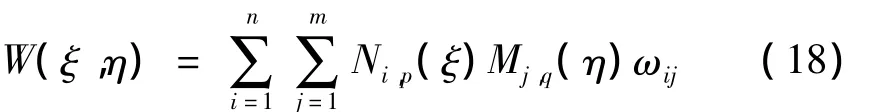
NURBS曲面定义为:
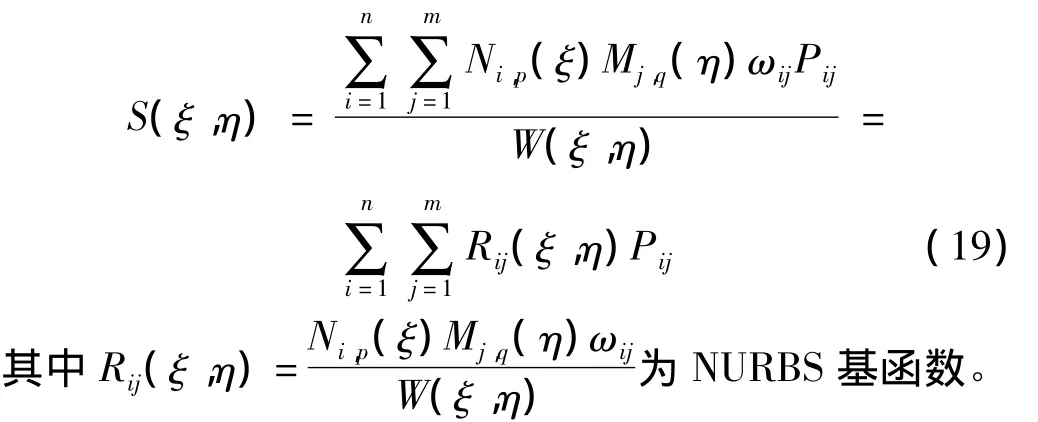
2.3 等几何有限元位移模式
等几何有限元法采用NURBS基函数作为结点形函数,将控制节点下标ij重新编号为A,其位移逼近可表示为:
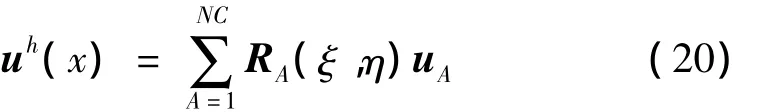
其中:uA=[uAvAwAβxAβyA]T为控制节点A广义位移矢量;NC表示控制节点数目;RA为控制节点A处形函数矩阵,是主对角线元素为RA的5阶对角方阵。
3 功能梯度板自由振动等几何有限元控制方程
首先给出基于一阶剪切板理论等几何有限元单元中应变场和曲率场的计算。由式(4)~(6)、(20)得单元中面面内应变场、曲率场以及横向剪应变场为:
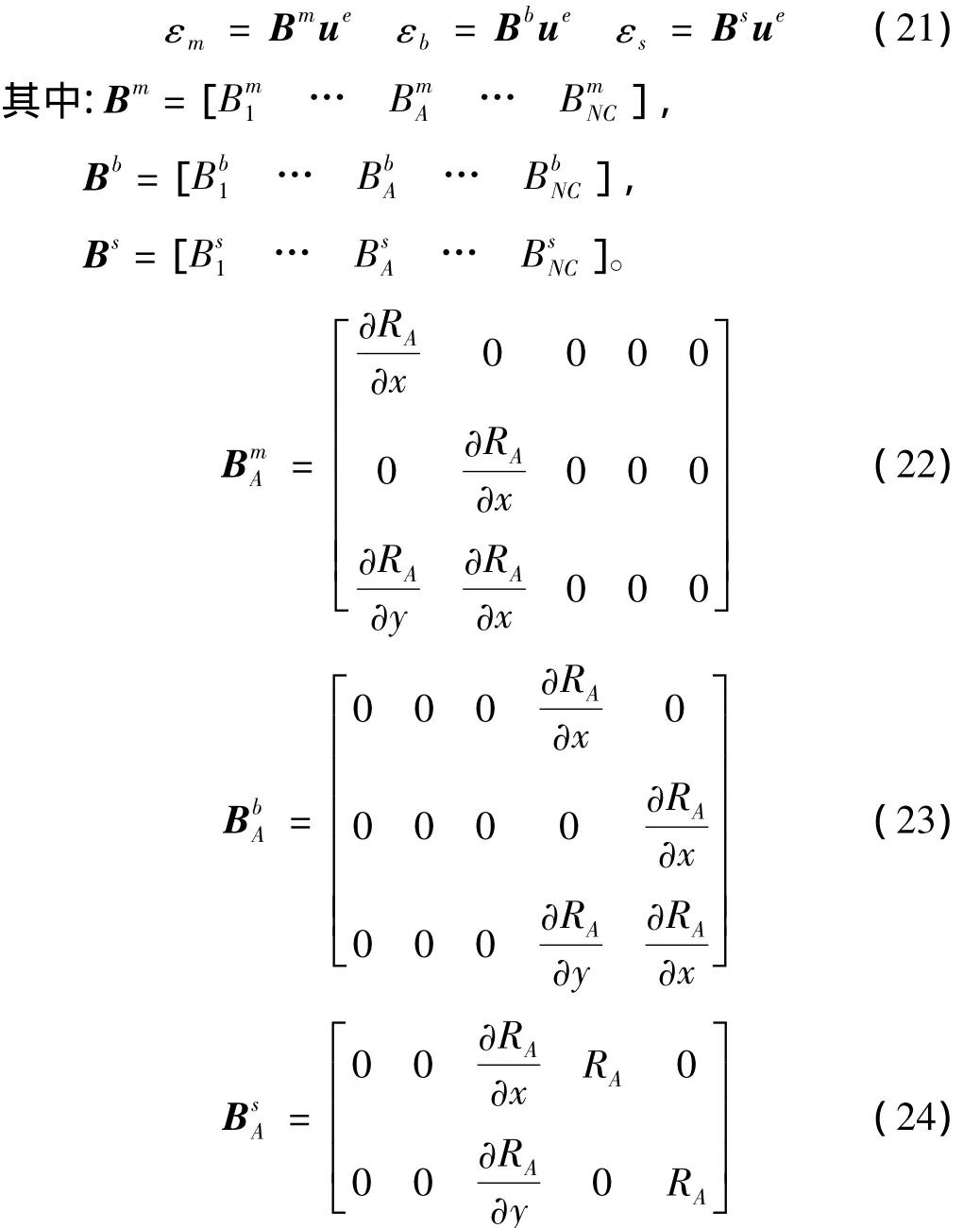
自由振动问题的特征方程为
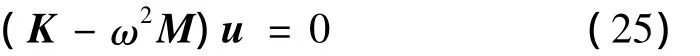
其中:K和M分别为整体劲度矩阵和质量矩阵,ω为自振频率。
单元对K的贡献可表示为:
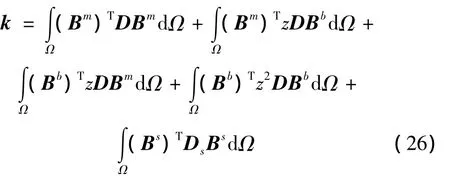
单元对M的贡献可表示为:
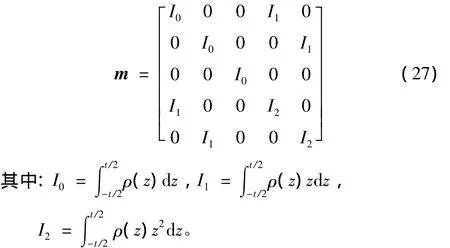
4 数值算例
4.1 四边简支Al/Al2 O3方板
图2为长厚比L/t=5的四边简支Al/Al2O3方板。板的材料参数为:Aluminum(Al)的弹性模量Em=70 GPa,泊松比 νm=0.3,密度 ρm=2 707 kg·m-3;Alumina(Al2O3)的弹性模量 Ec=380 GPa,泊松比 νc=0.3,密度 ρc=3 800 kg·m-3。梯度指数 n =0、0.5、1、4、10,分别计算板的自振频率。采用四种计算网格(8×8个控制节点、14×14个控制节点、20×20个控制节点、24×24个控制节点),每种计算网格分别采用非线性参数化网格[1]和线性参数化网格[1]。8×8个控制节点的非线性参数化网格和线性参数化网格如图3。表1和表2分别给出了不同阶次非线性参数化网格和线性参数化网格求解的第一阶归一化自振频率(由表1和表2可知,基于非线性参数化网格和线性参数化网格都能获得收敛的解答,但线性参数化网格求解精度高和收敛速度快,与文献[18]常规材料所得结果一致。本文后续算例均采用线性参数化网格,控制节点数为20×20,基函数阶次为p=q=3。
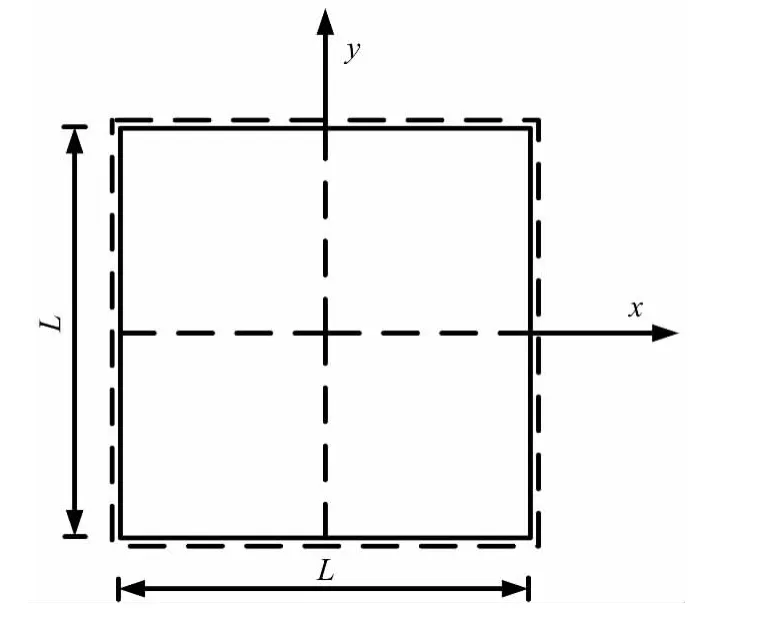
图2 四边简支的方形板Fig.2 Simply supported square plate
针对三种不同的板长厚比,分析了梯度指数对第一阶 自振频 率的影 响,并 与采 用 ES-DSG3[16]、MITC4[16]、HSDT[19]、kp-Ritz[14]和解析法[20]的结果做比较,见图4。归一化频率β=ω/ω*,ω为第一阶自振频率的数值解,ω*第一阶自振频率的解析解[20]。由图4可知,本文方法求解精度优于其它数值方法。L/t=20时,各种数值解在n=0.5时的结果与精确解的偏差明显大于其他梯度指数时所对应的偏差,其原因尚未有合理的解释。
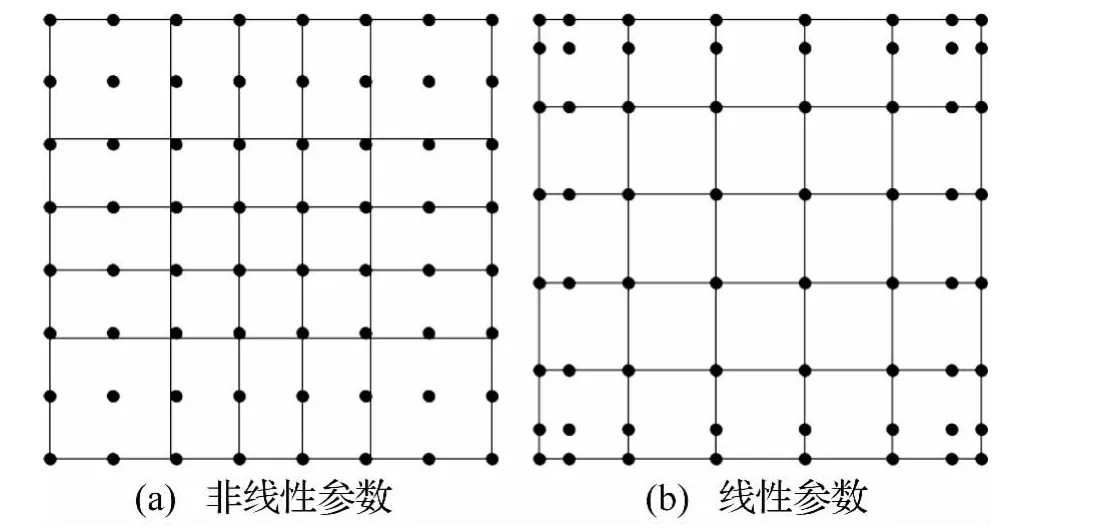
图3 8×8个控制节点的两种网格(p=q=3)Fig.3 Two meshesof 8 ×8 control points(p=q=3)
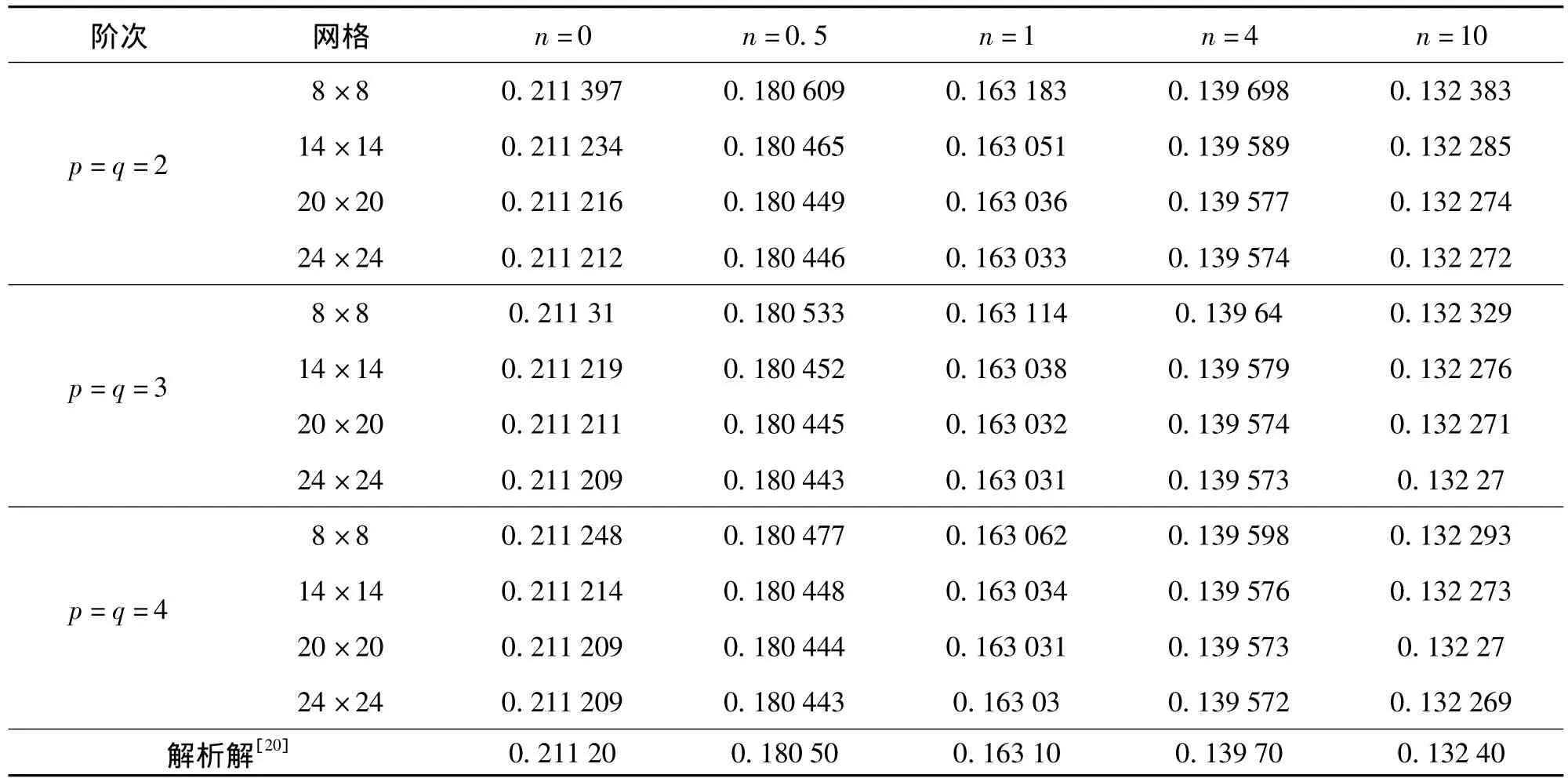
表1 非线性参数化网格第一阶归一化频率Tab.1 The normalized first frequency with nonlinear parameterization mesh
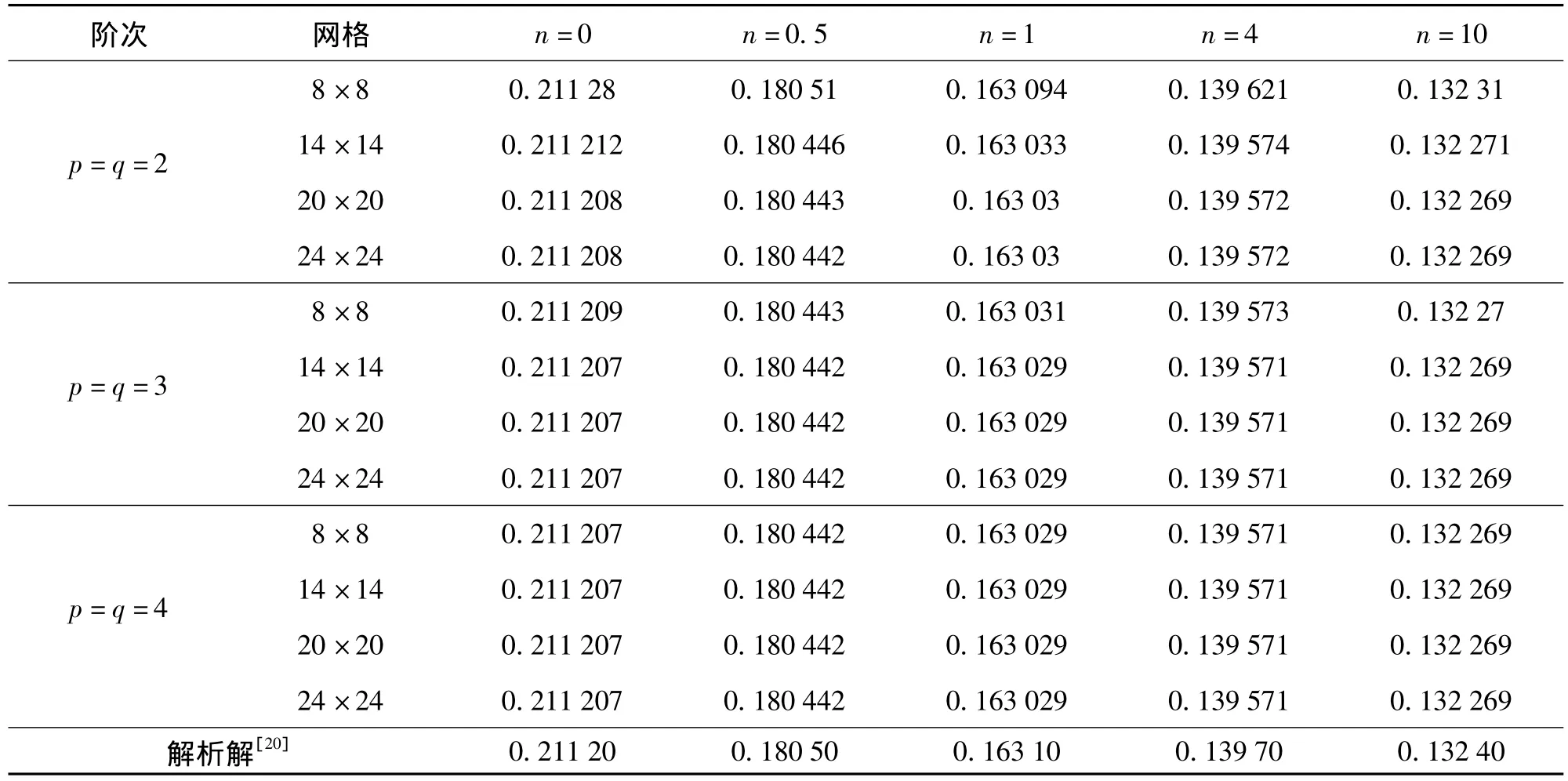
表2 线性参数化网格第一阶归一化频率Tab.2 The normalized first frequency with linear parameterization mesh
4.2 四边简支Ti-6Al-4V/Aluminum oxide方板
四边简支的Ti-6Al-4V/Aluminum oxide方板的几何尺寸为 L=0.4 m,t=0.005 m;材料参数为:Ti-6Al-4V的弹性模量 Em=105.7 GPa,泊松比 νm=0.298 1,密度 ρm=4 429 kg·m-3;Aluminum oxide 的弹性模量 Ec=320.2 GPa,泊松比 νc=0.26,密度 ρc=3 750 kg·m-3。表3和表4分别给出了梯度指数为n=0和n=2 000时采用不同方法获得的Ti-6Al-4V/Aluminum oxide功能梯度板前10阶自然频率。由表3和表4可知本文计算结果与 Bishop 等[21]、Zhao等[14]以及He等[10]计算结果相符。需要说明的是这两个表中有些频率值相同,但其振型并不同,由于篇幅限制,此处没给出振型图。
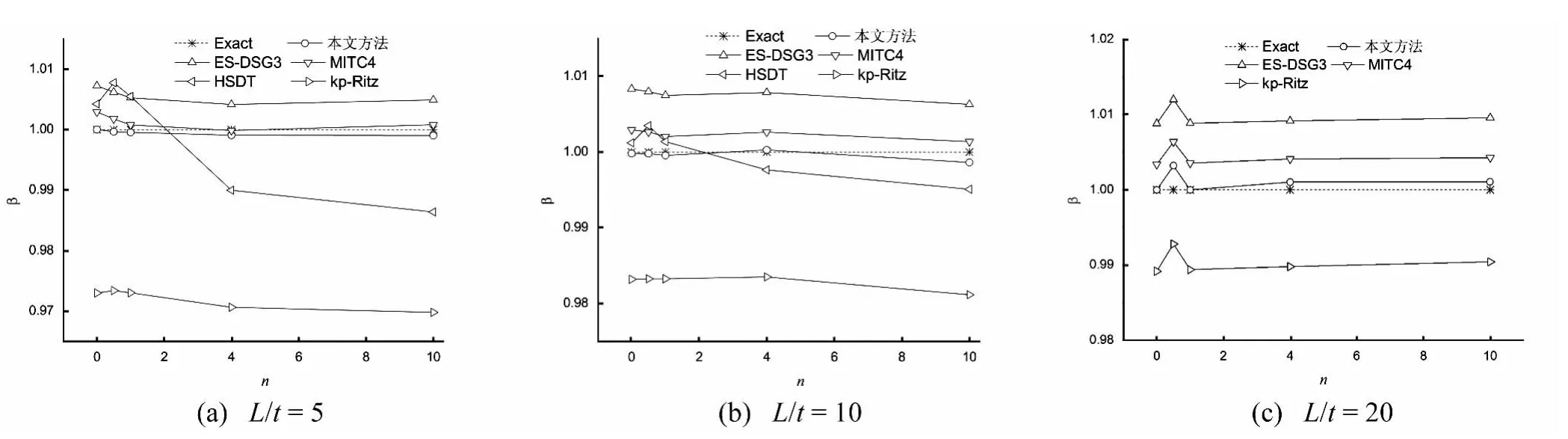
图4 归一化第一阶频率与梯度指数的关系Fig.4 The normalized first frequency versus gradient index
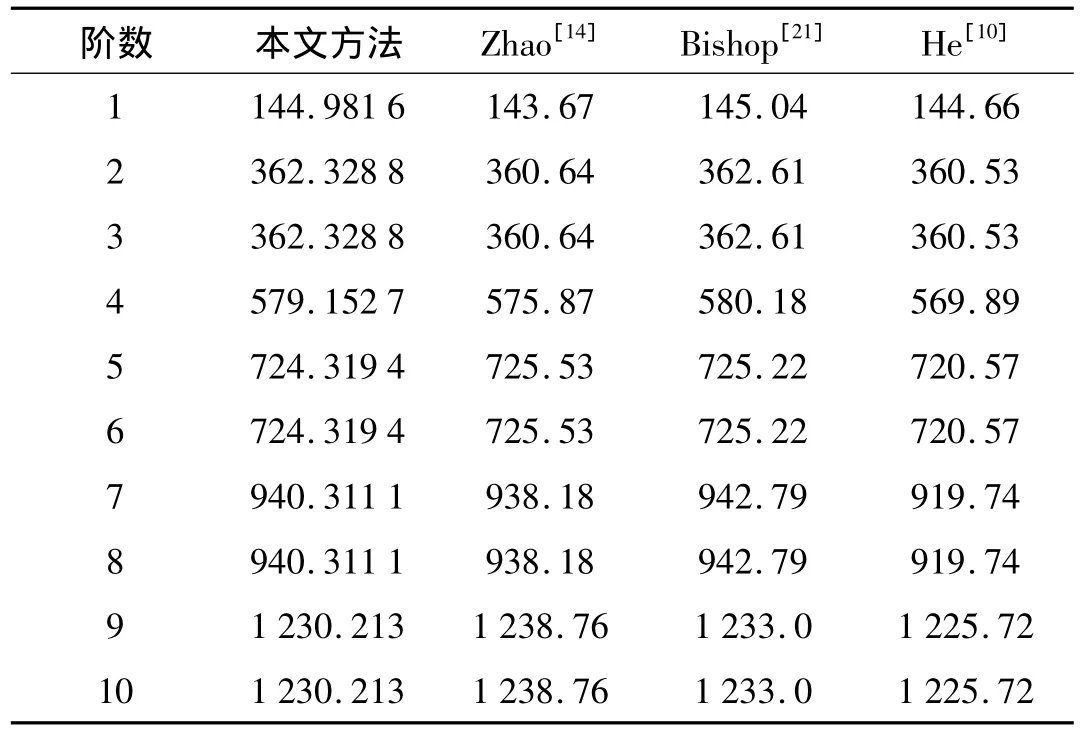
表3 n=0前10阶自然频率(Hz)Tab.3 The former 10 natural frequencies with n=0(Hz)
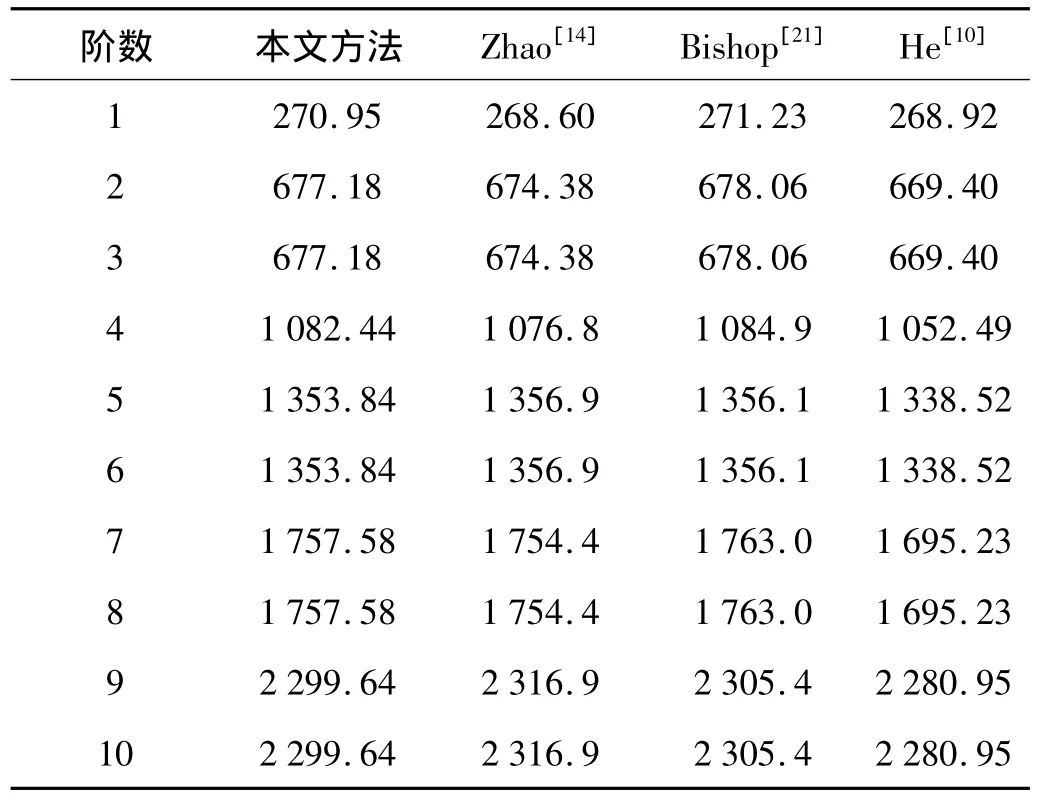
表4 n=2 000前10阶自然频率(Hz)Tab.4 The former 10 natural frequencies with n=2 000(Hz)
4.3 梯度指数、边界条件及长厚比对自振频率的影响
考虑 A l/Al2O3,Al/ZrO2,Ti-6Al-4V/Aluminum oxide和SUS304/Si3N4四种材料的方板,分析梯度指数、边界条件及长厚比对自振频率的影响。Al、Al2O3、Ti-6Al-4V和Aluminum oxide的材料参数同前两个算例;Zirconia(ZrO2)的弹性模量Ec=151 GPa,泊松比νc=0.3,密度 ρc=3 000 kg·m-3;SUS304 的弹性模量Em=207.78 GPa,泊松比 νm=0.317 7,密度 ρm=8 166 kg·m-3;Si3N4的弹性模量 Ec=322.27 GPa,泊松比 νc=0.24,密度 ρc=2 370 kg·m-3。归一化频率为 ω*=
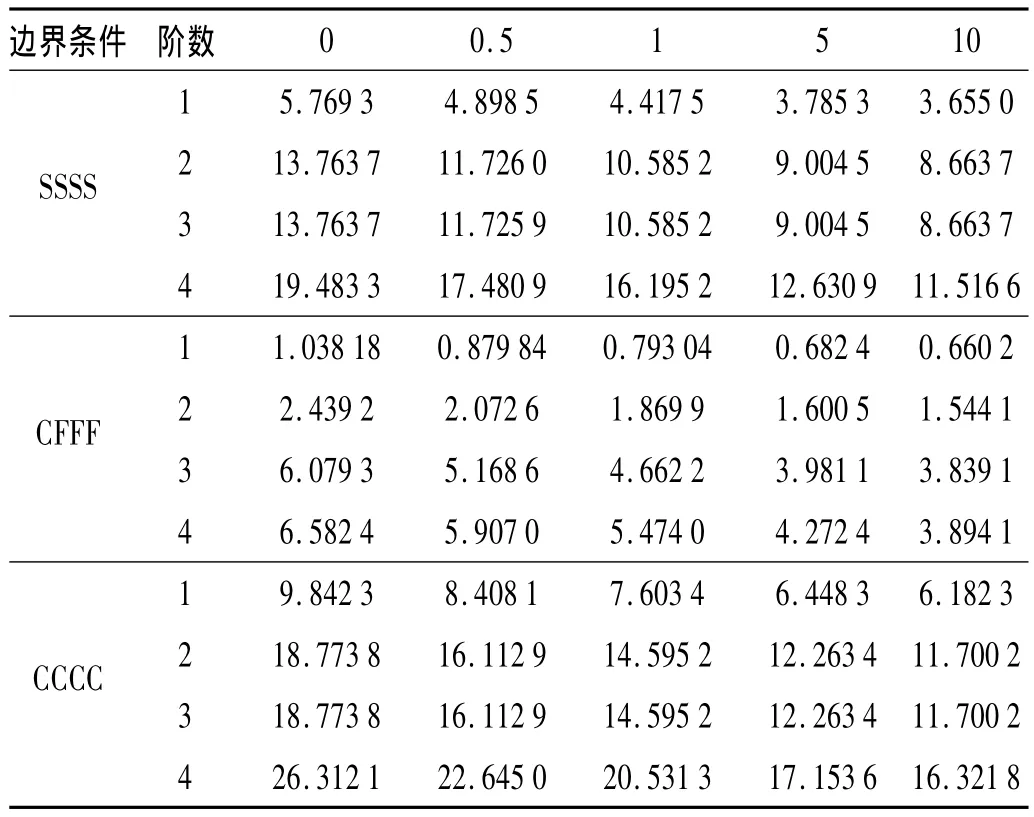
表5 不同梯度指数时Al/Al2O3方板的归一化频率Tab.5 The normalized frequencies versus gradient index for square Al/Al2O3 plate
表5给出了长厚比L/t=10的Al/Al2O3板在四边简支(SSSS),底边固支三边自由(CFFF)以及四边固支(CCCC)条件下前四阶归一化频率,该结果与zhao[14]计算结果相符。由表5可知,频率随着梯度指数的增加而减小。这与事实相符,因为梯度指数增加,板中陶瓷成分减少,板的整体刚度减小。对于Al/ZrO2,Ti-6Al-4V/Aluminum oxide和SUS304/Si3N4板可以得到类似的结果,如图5。从图5可知,随着梯度指数增加,自振频率减小;Al/Al2O3和Ti-6Al-4V/Aluminum oxide自振频率相接近;Al/ZrO2自振频率最大;SUS304/Si3N4自振频率最小。当梯度指数在0-2之间变化时,自振频率降低最快;梯度指数大于5以后自振频率变化不大。另外,由表5和图5可知,板的约束越大,其频率越大。
图6给出了梯度指数和长厚比对四边简支Al/ZrO2板和四边固支SUS304/Si3N4板第一阶归一化频率的影响。由图6可知,相同梯度指数,自振频率随长厚比增加而增大,当长厚比L/t=20后自振频率变化不大。
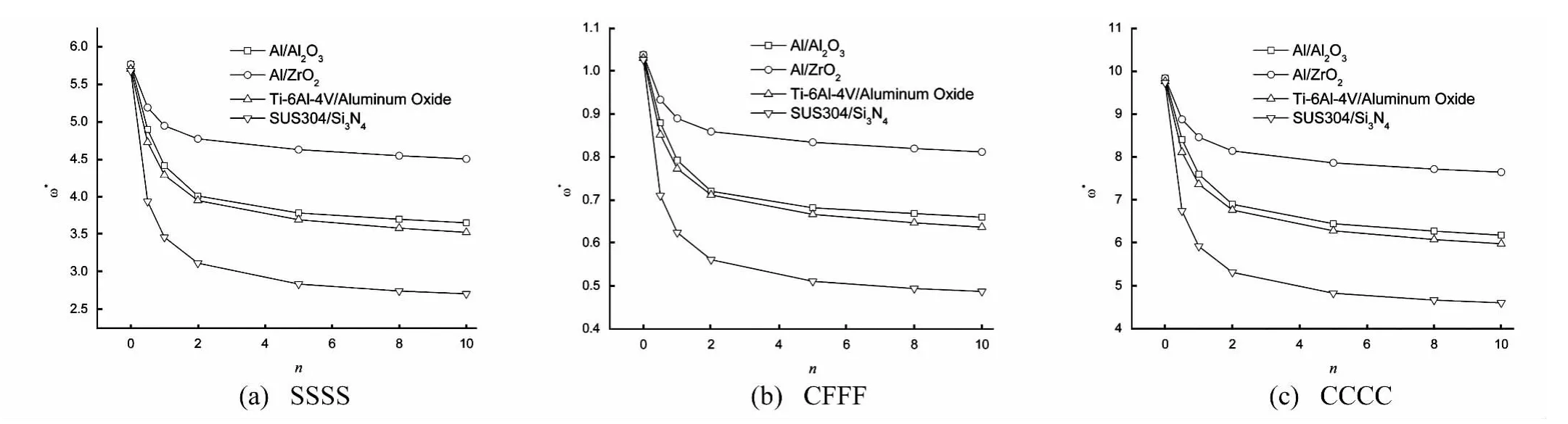
图5 第一阶归一化频率与梯度指数的关系Fig.5 The normalized first frequency versus gradient index
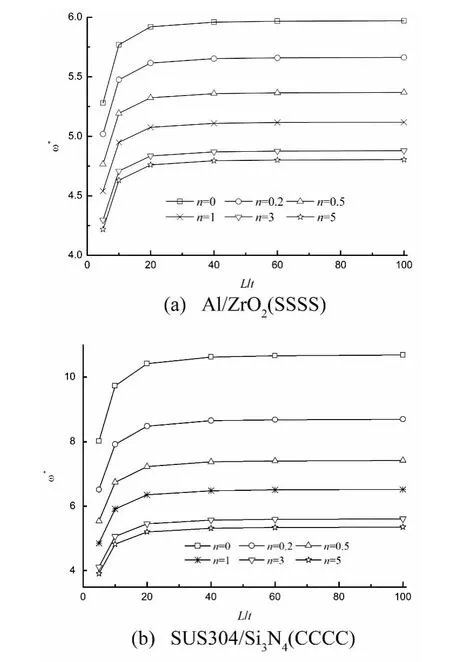
图6 第一阶归一化频率与长厚比的关系Fig.6 The normalized first frequency versus length-to-thickness ratio
5 结论
基于一阶剪切变形理论,建立了分析了功能梯度材料板自由振动问题的NURBS等几何有限元格式,分析了四种典型功能梯度材料板自振频率。算例分析表明等几何有限元法求解精度高和收敛速度快的优点。本文推广了等几何有限元应用范围。
本文仅讨论了基于一阶剪切变形理论的等几何有限元法。下一步将等几何有限元用于功能梯度板的几何非线性分析;对于薄板,有效消除剪切自锁的方法也有待进一步研究。
[1] Hughes T J R,Cottrell J A,Bazilevs Y.Isogeometric analysis:CAD,finite elements,NURBS,exact geometry and mesh refinement[J]. Computer Methods in Applied Mechanics and Engineering,2005,194(39-41):4135-4195.
[2] Hsu M C,Akkerman I,Bazilevs Y.High-performance computing of wind turbine aerodynamics using isogeometric analysis[J].Computers& Fluids,2011,49(1):93-100.
[3] Benson D J,Bazilevs Y,Hsu M C,et al.Isogeometric shell analysis:The Reissner-Mindlin shell[J].Computer Methods in Applied Mechanics and Engineering,2009,199(5-8):276-289.
[4] Buffa A,Sangalli G,Vázquez R.Isogeometric analysis in electromagnetics:B-splines approximation [J].Computer Methods in Applied Mechanics and Engineering,2010,199(17):1143-1152.
[5]Gómez H,Calo V M,Bazilevs Y,et al.Isogeometric analysis of the Cahn-Hilliard phase-field model[J].Computer Methods in Applied Mechanics and Engineering,2008,197(49-50):4333-4352.
[6] Seo Y D,Kim H J,Youn S K.Isogeometric topology optimization using trimmed spline surfaces[J].Computer Methods in Applied Mechanics and Engineering,2010,199(49-52):3270-3296.
[7] VerhooselC V,Scott M A,Renéde Borst,et al.An isogeometric approach to cohesive zone modeling [J].International Journal for Numerical Methods in Engineering,2011,87(1-5):336-360.
[8] Ghorashi S S, Valizadeh N, Mohammadi S. Extended isogeometric analysis for simulation of stationary and propagating cracks[J].International Journal for Numerical Methods in Engineering,2011,89(9):1069-1101.
[9] Koizumi M.FGM activities inJapan[J].Composites,1997,28(1–2):1-4.
[10] He X Q,Ng T Y,Sivashanker S,et al.Active control of FGM plates with integrated piezoelectric sensors and actuators[J].International Journal of Solids and Structures,2001,38(9):1641-1655.
[11] Sundararajan N,Prakash T,Ganapathi M.Nonlinear free fl exural vibrations of functionally graded rectangular and skew plates under thermal environments[J].Finite Elements in Analysis and Design,2005,42(2):152-168.
[12] Reddy J N.Analysis of functionally graded plates[J].International Journal for Numerical Methods in Engineering,2000,47(1-3):663-684.
[13] Lee Y Y,Zhao X,Liew K M.Thermoelastic analysis of functionally graded plates using the element-free kp-Ritz method[J].Smart Materials and Structures,2009,18(3):035007.1-035007.15.
[14] Zhao X,Lee Y Y,Liew K M.Free vibration analysis of functionally graded plates using the element-free kp-Ritz method[J].Journal of Sound and Vibration,2009,319(3-5):918-939.
[15] Nguyen-Xuan H,Tran L V,Thai H,et al.Analysis of functionally graded plates by an eきcient finite element method with node-based strain smoothing[J]. Thin-Walled Structures,2012,54:1-18.
[16] Nguyen-Xuan H,Tran L V,Nguyen-Thoi T,et al.Analysis of functionally graded plates using an edge-based smoothed finite element method [J].Composite Structures,2011,93(11):3019-3039.
[17]Piegl L A,Tiller W.The NURBSBook[M].Second ed.,New York,Springer-Verlag,1997.
[18] Shojaee S,Valizadeh N,Izadpanah E,et al.Free vibration and buckling analysis of laminated composite plates using the NURBS-based isogeometric finite element method [J].Composite Structures,2012,94(5):1677-1693.
[19] Matsunaga H.Free vibration and stability of functionally graded plates according to a 2D higher-order deformation theory[J].Composite Structures,2008,82(4):499-512.
[20] Hosseini-Hashemi Sh,Fadaee M,Atashipour S R.A new exact analytical approach for free vibration of Reissner-Mindlin functionally graded rectangular plates [J].International Journal of Mechanical Sciences,2011,53(1):11-22.
[21] Bishop R E D,Johnson D C.The mechanics of vibration[M].Cambridge,United Kingdom,Cambridge University press,2011.
