冷轧液压辊缝系统的自适应模糊Backstepping控制
2013-05-24吴忠强汤雅超肖雪飞于金平
吴忠强,汤雅超,肖雪飞,于金平
(1.国家冷轧板带装备及工艺工程技术研究中心,秦皇岛 0 66004;2.燕山大学 工业计算机控制工程河北省重点实验室,秦皇岛 0 66004)
冷轧机辊缝系统的控制是板厚控制的核心技术。在现代轧机板厚控制系统中,电液伺服控制系统以其响应速度快、控制精度高、体积小、质量轻等优点占据了主导地位。但是,电液伺服控制系统具有很强的非线性特性,系统中的参数存在不确定性,给控制系统的设计带来很大的困难[1]。由于线性控制策略往往得不到理想的控制效果,人们将非线性智能控制方法应用到板厚自动控制系统中:赵琳琳等[2]利用自适应鲁棒控制方法设计了动态控制器;李迅等[3]将Smith预测方法应用到AGC控制系统中;Bemporad等[4]利用最优滑模方法进行AGC控制。以上方法都在一定程度上改善了AGC系统性能。
Backstepping设计方法的基本思路是将一个复杂的高阶系统分解成若干个子系统,递归地对各个子系统进行Lyapunov函数选择和控制器设计直至完成对整个系统的设计,从而有效地避开了直接选取高阶系统Lyapunov函数的难题。Backstepping设计方法因其具有设计思路简单、步骤清晰等优点而被广泛应用。Hang等[5]提出了一类严格反馈非线性系统的自适应Backstepping控制;Ge等[6]基于 Backstepping方法提出了非线性系统自适应神经网络控制;Yang等[7]提出了基于小增益和Backstepping的鲁棒自适应模糊控制器;Zhou等[8]对带有输入延时的不确定系统设计了Backstepping自适应控制;李渊等[9]将Backstepping方法应用到双馈电机系统中,设计了滑模变结构控制器。
文献[10-11]针对电液伺服系统采用了标准的Backstepping设计方法分别设计了多滑模鲁棒自适应控制和自适应滑模控制,由于电液伺服系统中含有较多的不确定参数,使得控制器中含有大量的自适应律,加之Backstepping设计过程中对状态量反复求导引起的计算膨胀问题,导致控制器设计复杂,很难得到最优的控制效果。贾涛等[12]应用了模糊自适应方法,解决了Backstepping方法的计算膨胀问题,使控制效果得到了改善。
本文针对液压辊缝系统的非线性、参数不确定性和负载干扰提出了一种自适应模糊Backstepping滑模控制方法。用模糊系统来逼近参数不确定项和干扰项,解决了大量自适应律嵌套在控制器中的问题。选取适当Lyapunov函数,有效地减少了Backstepping设计步骤,抑制了Backstepping设计过程中的计算膨胀。仿真表明,本控制器能实现快速跟踪,对参数变化和负载干扰具有较强的鲁棒性。
1 液压-辊系模型及问题描述
冷轧液压辊缝系统是由四通滑阀、双头液压缸和机架轧辊系统组成。
假设四通阀为理想的零开口滑阀,根据流体力学节流公式和压力分析可得四通阀的压力-流量方程:
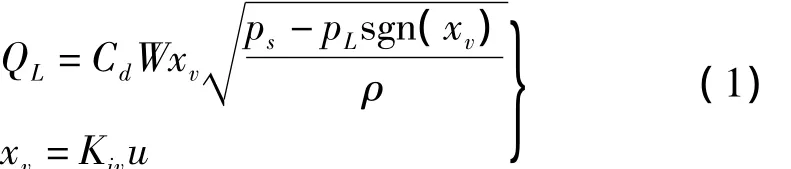
其中:xv为阀芯位移;Kiv为伺服放大器的放大倍数;QL为负载流量;Cd为节流口流量系数;W为节流口面积梯度;ps,pL分别为油源压力和负载压力;ρ为液压油密度;u为控制器输出。
假设液压缸的负载流量是两个工作腔流量的平均值,综合每个工作腔的流量连续方程可得油缸的流量连续方程:

其中:Ct为液压缸的总的泄露系数;A为液压缸活塞的有效面积;Vt为液压缸等效的总容积;xp为液压缸输出位移;β为液体体积弹性模量。
液压缸的动态特性受负载特性的影响,冷轧液压系统的负载力包括粘性阻力、弹性阻力、外部负载力和惯性力。将轧机辊系近似为单自由度模型,认为在轧制的过程中下辊系是固定不动的,只有上辊系做垂直运动,则有液压缸输出力平衡方程:
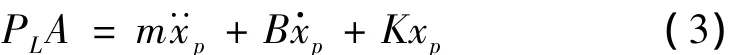
其中:m为折算到活塞上的总的等效质量;B为轧机粘性阻尼系数;K为轧机弹性刚度系数。
假设液压缸活塞杆与轧辊刚性连接,液压缸缸体与机架刚性连接,工作辊与支撑辊是弹簧-阻尼连接,可建立轧机机架-辊系和液压缸的动力学方程:
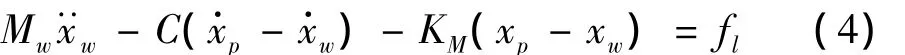
其中:xw为工作辊位移;Mw为工作辊及其轴承的等效质量;C为工作辊与支撑辊间的阻尼系数;KM为轧辊间弹性系数;fl为外部负载力。

控制目标是使系统快速跟踪给定的参考轨迹并保持稳定。本文采用Backstepping方法设计滑模控制器,利用自适应模糊系统来逼近不确定项和干扰项,从而消除不确定项和干扰项对系统稳定性的影响,最终使系统工作在稳定的工作状态。


Ωf、Ωg和 Ω0分别是 ωf、ωg和 x的有界集。根据模糊系统的万能逼近定理,f(x)、g(x)的最优逼近分别为:
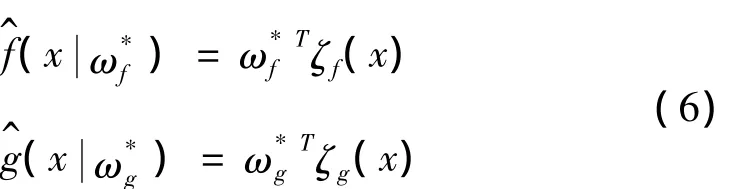
定义逼近误差:
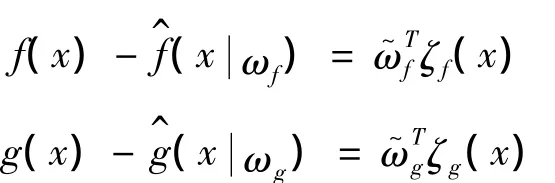
2 控制器设计及稳定性分析
对液压辊缝系统进行自适应模糊Backstepping滑模控制器设计,选取适当的Lyapunov函数使得三步Backstepping就能完成对五阶系统的控制器设计,解决高阶系统Backstepping设计的计算膨胀问题,在Backstepping设计的最后一步与滑模控制方法相结合,进一步提高系统的鲁棒性,最后证明设计的控制器能够使系统渐近稳定。
第一步,首先考虑子系统(x1,x2),选取Lyapunov函数

则V1沿着子系统(x1,x2)的时间导数为:

选取
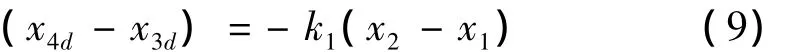
为虚拟控制输入,其中k1为选定的正常数。
令 α1=e4-e3=(x4-x3)-(x4d-x3d)
其中 x3d,x4d为 x3,x4的期望值。那么

第二步,考虑子系统(x1,x2,x3,x4),选取 Lyapunov函数

其中rf为选定的正常数。有:

选取

为虚拟控制输入,其中k2为选定的正常数。
令α2=e5=x5-x5d,其中x5d为x5的期望值。则

所以自适应律取

则

第三步,定义滑动流形为

其中c1为选定的正常数。
对s求导有
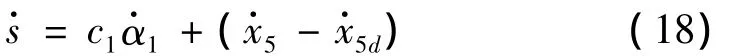
定义 η - η^= η~。
考虑整个系统,选取Lyapunov函数
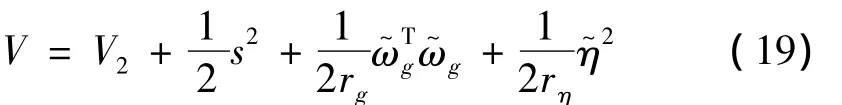
其中 rg,rη为选定的正常数,有

取自适应滑模控制器
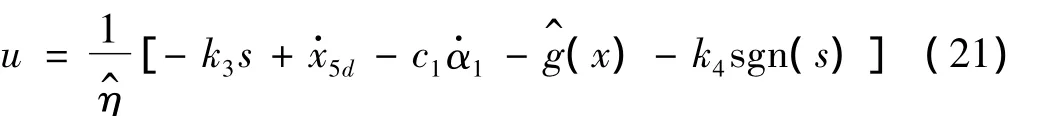
其中k4是选定的正常数。将式(21)代入式(20)有
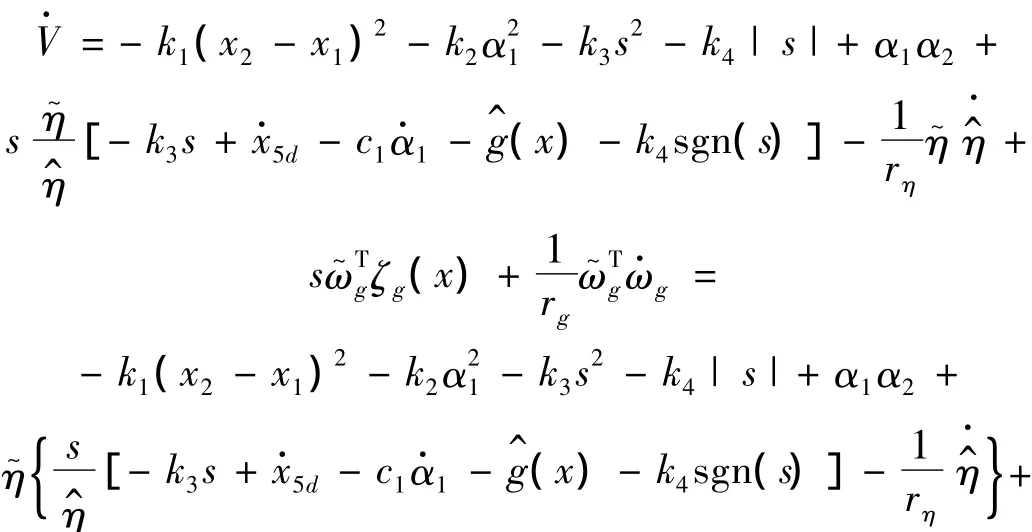
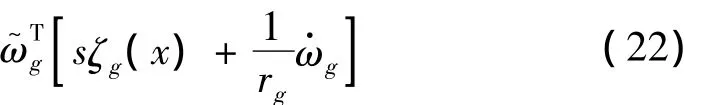
取自适应律:

将上述自适应律代入到式(22)中可得:
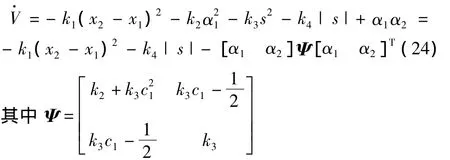
当控制器的参数满足下列不等式时,
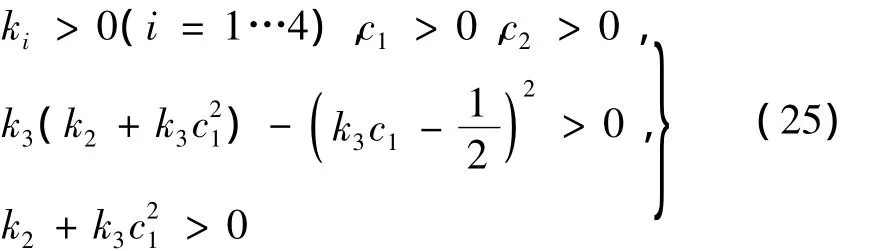
矩阵Ψ的一、二阶顺序主子式全都大于零,所以矩阵Ψ是正 定 的。由 式 ( 24)可 知·V≤ - [α1α2] ×Ψ[α1α2]T,因此有[α1α2]Ψ[α1α2]Td t≤V(0)-V(∞)。又因为(x2- x1)、α1、α2、s、都是有界的,所以 V 有界。由 B arbalat定理可知[α1α2]Ψ[α1α2]T=0,所以有=0(i=1,2),就是系统的跟踪误差收敛。同理,即整个系统可以实现对给定信号的跟踪,系统状态将沿着期望的轨迹趋近于滑模面s=0,因此系统渐近稳定。
3 仿真研究
为验证该控制方法的有效性,对某厂四辊轧机进行参数取样,并对系统参数发生变化前后,自适应模糊Backstepping控制器与经典Backstepping控制器的响应曲线进行比较:
在式(5)所示的冷轧机电液伺服系统中,主要的参数为:A=0.68 m2;m=84.2×103kg;B=9×105Ns/m;K=6 ×1010N/m;KM=5.6 ×1010N/m;Ct=5 ×10-13m3s/Pa;Vt=0.144 m3;β =7 ×108Pa;Kq=2.6 ×10-2m2/s;Ps=1 ×107Pa;ρ=900 kg/m3;Kiv=0.004;Mw=9.2 ×103kg;C=11.38 ×105Ns/m。
控制器参数:k1=10 000,k2=662,k3=16.5,k4=350,rf=0.05,rg=1,rη=0.000 1,c1=1。
模糊集合对应的隶属函数取为
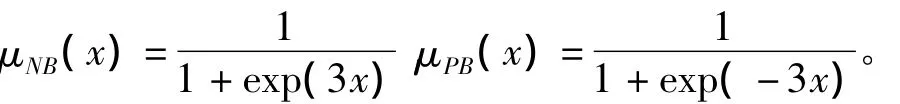
轧机的工作环境恶劣,会因带钢的温度、厚度、密度、材质的分布不均、机械的振动和焊接点等不确定的因素造成负载的质量、粘性阻尼系数、弹性模量等会发生改变。考虑系统参数的慢时变特性,主要是以下参数发生变化:m=90×103kg,B=8.5 ×105Ns/m,K=5.5 ×1010N/m,C=10.5 ×105Ns/m,Ct=5.5 ×10-13m3s/Pa,Mw=9.0 ×103kg。
轧机轧制过程分为三个不同的工作阶段:上下工作辊靠近阶段、上下工作辊压靠阶段、正常轧制阶段。然而上下工作辊压靠阶段和正常轧制阶段联系紧密,负载特性相似,所以将其视为一个工作阶段。下面从上下工作辊靠近阶段、压靠-正常轧制阶段两个阶段对控制器的效果进行验证:
(1)在实际轧制过程中,冷轧机在准备轧制前要先将两工作辊靠近,这一过程中两工作辊之间没有相互挤压,所以负载轧制力fl=0,系统无负载干扰。液压系统由静止状态启动,从0 mm位置移到20 mm即满足这一工艺要求。图1、图2表明本控制算法与经典Backstepping控制算法相比对系统的参数变化具有较强的鲁棒性,同时具有快速性和准确性,能够满足轧钢生产本阶段的要求。

图1 跟踪20 mm位移输出响应曲线Fig.1 The output response curve of tracking 20 mm displacement
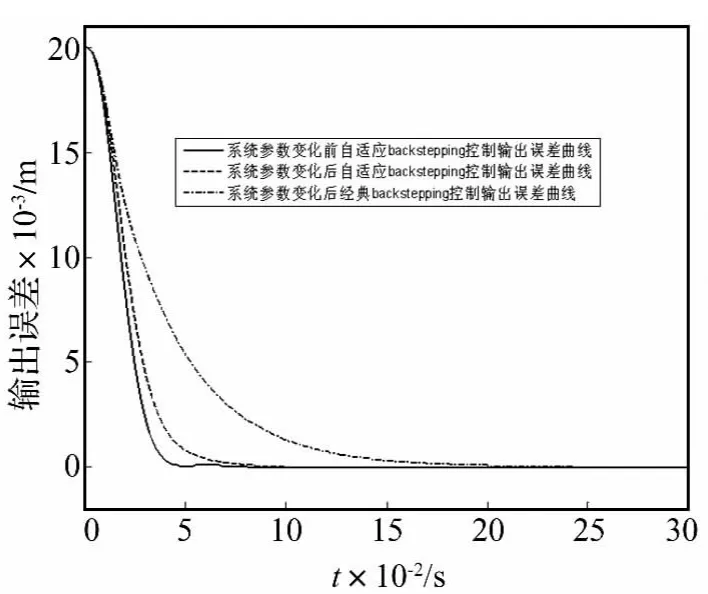
图2 跟踪20 mm位移误差曲线Fig.2 The error curve of tracking 20 mm displacement
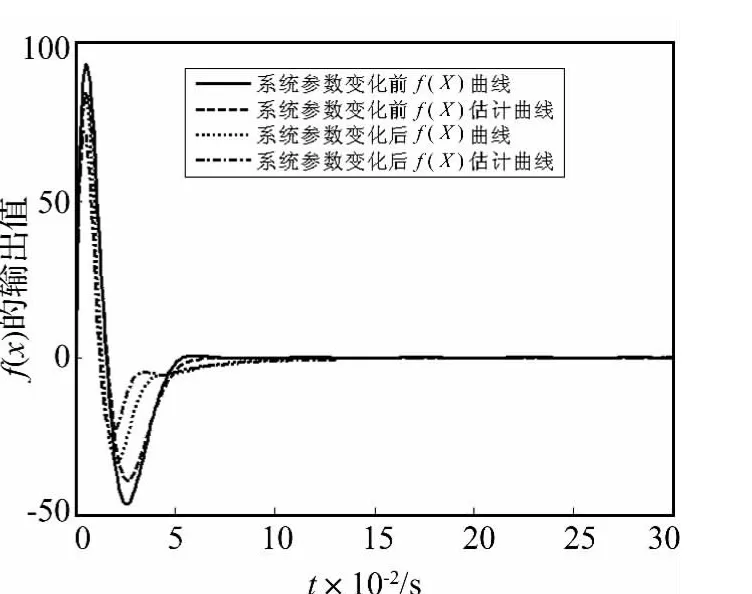
图3 f(x)的自适应模糊估计曲线Fig.3 Theadaptive fuzzy estimation curve of f(x)
图3和图4表示系统参数改变前后,上下工作辊靠近阶段自适应模糊系统对f(x)和g(x)的估计曲线,由图可知自适应模糊系统可以在短时间内准确估计出非线性函数。图5是系统参数变化前后,上下工作辊靠近阶段控制系统η的自适应估计曲线。
(2)压靠过程:为了消除小轧制力区不稳定的影响,在轧机中没有带钢的情况下,将上下工作辊压靠在一起,产生较大轧制力的过程。这一过程要求两工作辊压靠距离为1 mm。如图6、图7所示,0~0.1 s为压靠过程,工作辊快速压靠并且在0.07 s时误差远小于0.01 mm,表明本控制算法可以实现轧机系统的快速压靠,使轧制力迅速达到正常轧制生产的要求,达到消除小轧制力区不稳定影响的要求,使轧机系统快速过度到正常的轧制过程。
(3)正常轧制过程:板带在轧制的过程中存在加工硬化现象,带钢的温度、厚度、密度、材质的分布不均、机械的振动和焊接点等不确定的因素造成负载的质量、粘性阻尼系数、弹性模量等会发生改变,这些因素都能够造成轧制力突变。为了对实际的生产过程中的干扰进行仿真,在0.05 s后令轧制力突变为fl=1.34×107N,符合正常轧制生产的要求。图6和图7的0.1秒以后输出的曲线表示正常轧制过程响应曲线。表明该控制算法可以有效地消除轧制过程负载扰动的影响,使系统稳定的跟踪指定位置。
由图6、图7可知自适应模糊Backstepping控制算法比经典Backstepping算法更能适应系统参数的变化,使系统得到更好的性能。
图8和图9表示系统参数改变前后,压靠-正常轧制阶段自适应模糊系统对f(x)和g(x)的估计曲线,由图可知自适应模糊系统可以在短时间内准确估计出非线性函数。图10是系统参数改变前后,压靠-正常轧制阶段控制系统η的自适应估计曲线。
通过上述三个工作过程可以表明:在系统的参数改变前后,该控制器都能够使系统快速跟踪指定位置,使位置误差收敛到0.01mm以内,克服系统参数的不确定性,对负载的扰动具有较强的鲁棒性,控制器实用有效。

图4 g(x)的自适应模糊估计曲线Fig.4 Theadaptive fuzzy estimation curve of g(x)

图5 η的自适应估计曲线Fig.5 Adaptive estimation curve ofη

图6 压靠-正常轧制输出响应曲线Fig.6 The output response curve of under pressure-normal rolling

图7 压靠-正常轧制误差曲线Fig.7 The error curve of under pressure-normal rolling
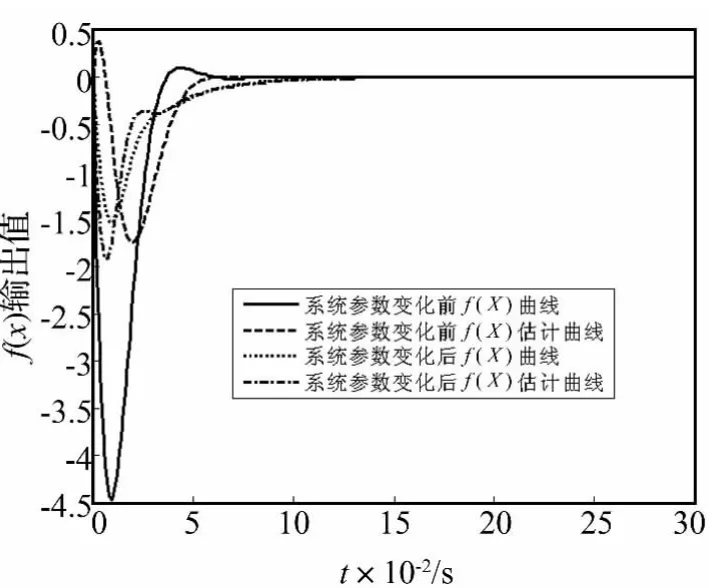
图8 压靠-正常轧制f(x)的自适应模糊估计曲线Fig.8 The adaptive fuzzy estimation curve of f(x)of under pressure-normal rolling

图9 压靠-正常轧制g(x)的自适应模糊估计曲线Fig.9 The adaptive fuzzy estimation curve of g(x)of under pressure-normal rolling
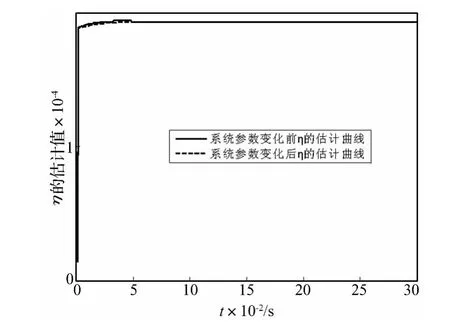
图10 压靠-正常轧制η的自适应估计曲线Fig.10 Adaptive estimation curve ofη of under pressure-normal rolling
4 结论
本文综合考虑冷轧液压辊缝系统的非线性、参数不确定性和负载干扰,建立了五阶液压辊缝系统模型。设计了一种自适应模糊Backstepping滑模控制方法。利用自适应模糊系统对模型的不确定项和干扰项进行逼近,从而消除了不确定项和干扰项的影响。根据模型特征,选取适当的Lyapunov函数,使得三次反步算法就能够完成对五阶系统自适应模糊Backstepping滑模控制器的设计,有效地简化了设计过程,解决了高阶系统Backstepping设计的计算膨胀问题,在Backstepping设计的最后一步与滑模控制方法相结合,进一步提高了系统的鲁棒性。仿真结果表明,该控制器能使系统够快速准确地跟踪指定位置,对参数变化和外部干扰有较强的鲁棒性。控制器的设计步骤简单且易于实现,为工业现场的应用提供了新的控制方法。
[1]管 成,潘双夏.电液伺服系统的非线性鲁棒自适应控制[J].中国电机工程学报,2007,27(24):107-112.GUAN Cheng,PAN Shuang-xia.Nonlinear robust adaptive control of electro-hydraulic system[J].Proceedings of the CSEE,2007,27(24):107 -112.
[2]赵琳琳,方一鸣,钟伟峰,等.冷带轧机厚控系统自适应鲁棒输出反馈动态控制器设计[J].控制理论与应用,2008,25(4):787-790.ZHAO Lin-lin,FANG Yi-ming,ZHONG Wei-feng,et al.Design of adaptive robust output feedback dynamic controller for thickness control in a cold strip rolling mill[J].Control Theory& Applications,2008,25(4):787-790.
[3]李 迅,宋东球,喻寿益,等.基于模型参考自适应Smith预估器的反馈式AGC厚度控制系统[J].控制理论与应用,2009,26(9):999-1003.LI Xun,SONG Dong-qiu,YU Shou-yi,et al.Feedback automatic gauge control system using model reference adaptive Smith predictor[J].Control Theory & Applications,2009,26(9):999-1003.
[4]Bemporad A,Bernardini D,Cuzzola F A.Optimization-based automatic flatness control in cold tandem rolling[J].Journal of Process Control,2010,20(4):396 -407.
[5]Hang T,Ge SS,Hang CC.Adaptive neural network control for strict-feedback nonlinear systems using backstepping design[J].Automatica,2000,36(12):1835 -1846.
[6] Ge S Z,Wang C.Direct adaptive NN control of a class of nonlinear systems[J]. IEEE Transaction on Neural Networks,2002,13(1):214 -221.
[7] Yang Y S,Zhou C J.Adaptive fuzzy H∞stabilization for strict-feedback canonical nonlinear systems via backstepping and small-gain approach[J].IEEE Transactons on Fuzzy System,2005,13(1);101-114.
[8]Zhou J,Wen C Y,Wang W.Adaptive backstepping control of uncertain systems with unknown input time-delay[J],Automatica,2009,45(6):1415-1422.
[9]李 渊,何凤有,谭国俊.双馈电机系统滑模变结构反演控制的研究[J].电机与控制学报,2009,13(1):15-19.LI Yuan,HE Feng-you,TAN Guo-jun.Study on variable structure sliding mode control with backsepping for doubly-fed motor system[J].Electric Machines and Control,2009,13(1):15-19.
[10]管 成,朱善安.电液伺服系统的多滑模鲁棒自适应控制[J].控制理论与应用,2005,22(6):931 -938.GUAN Cheng,ZHU Shan-an.Multiple sliding mode robust adaptive control of an electro-hydraulic servo system[J].Control Theory & Applications,2005,22(6):931 -938.
[11] Guan C,Pan SX.Adaptive sliding mode control of electrichydraulic system with nonlinear unknown parameters[J].Control Engineering Practice,2008,16(11):1275-1284.
[12]贾 涛,刘 军,钱富才.一类非线性时滞系统的自适应模糊动态面控制[J].自动化学报,2011,37(1):83-91.JIA Tao,LIU Jun,QIAN Fu-cai.Adaptive fuzzy dynamic surface control for a class of nonlinear systems with unknown time-delays[J].Acta Automatica Sinica,2011,37(1):83-91.
