覆冰导线舞动作用下输电塔破坏机理的试验研究
2013-05-24楼文娟杨晓辉
杨 伦,楼文娟,陈 勇,阎 东,杨晓辉
(1.浙江大学 结构工程研究所,杭州 310058;2.河南电力试验研究院,郑州 450052)
覆冰导线舞动具有振幅大、持续时间长的特点,产生的大幅动态张拉力会导致输电塔构件撕裂或失稳、连接螺栓松动、横担失效甚至输电塔的倒塌等难以恢复的恶性事故,严重威胁电网系统的正常运行[1-3]。因此,研究输电塔线体系在舞动作用下的损伤原因和破坏机理,控制、减轻舞动对输电塔的危害,对保证输电线路的安全运行有着重要的工程价值和经济意义。
目前很多学者[4-6]基于静力加载试验,获得了输电塔在覆冰荷载或导线张力作用下的极限承载力以及失效模式,并给出了相应的安全评估[7]或结构加固方法[8]。但是输电塔在导线动力作用与静力作用下的破坏机制有着本质区别,因此不能以静力试验结果来推断结构在导线舞动作用下的失效模式或极限承载力。王昕[9]、荣志娟等[10]在输电塔线体系有限元模型的基础之上,研究了导线舞动对杆塔的作用特征。需要指出的是,以上数值模拟均限定结构材料处于弹性范围内,对舞动作用下杆塔破坏机理的探索尚未涉及。另外,张勇等[11]和谢强等[12]基于气弹模型风洞试验,考察了覆冰荷载对输电塔线体系风致振动响应的影响。然而受风洞尺寸的限制和模型缩尺效应的影响,风洞试验仅模拟了塔线体系在风荷载作用下的抖振响应,未能再现覆冰导线舞动时的动态特征。
受现有认知范围的限制,舞动导致输电塔破坏的机理至今尚不明确。就事故调查资料来看,引发输电塔破坏的可能原因主要有三种:①导线舞动产生的大幅动态张拉力造成输电塔构件失稳或者撕裂[13];②在长时间舞动作用下构件发生疲劳破坏,致使输电塔整体倾覆[14];③ 构件连接螺栓在舞动产生的大幅动态张拉力作用下发生松动,导致构件内力重新分配,造成输电塔的倒塌[15]。从研究手段来看,前两种导致输电塔可能破坏的原因可通过模型试验或者数值模拟进行考察;但是由于缺乏输电塔破坏前螺栓实际预紧状态的力学参数,上述的第三种破坏原因难以通过传统研究方法加以验证。
综上所述,针对以往研究的不足之处,本文以在舞动事故中遭受严重破坏的某转角耐张塔为研究对象,基于模型动力相似理论,设计制作覆冰导线模型和弹性边界条件下的大比例输电塔节段模型。同时,考虑到导线舞动形式以单个半波为主,且达到稳定时具有频率和振幅均保持不变的特征,研制用于模拟导线舞动的试验加载装置。在此基础上,鉴于舞动导致输电塔破坏的三种可能原因和研究方法的可实现性,采用排除法确定其破坏机理。其中具体工作内容分为三步:首先,结合破坏线路的现场覆冰参数和舞动幅值,进行舞动事故的反演,检验实际情况中输电塔的破坏是否由构件承载力不足所引起;其次,根据舞动试验测得的构件动应力幅值,采用规范提供的方法,计算输电塔在导线舞动作用下的疲劳寿命,考察构件在实际舞动时间作用下是否发生疲劳破坏;最后,综合分析塔线体系舞动试验和疲劳寿命的计算结果,确定覆冰导线舞动作用下输电塔失效的根本原因。
1 输电塔线体系舞动试验的介绍
1.1 输电塔线体系模型
输电塔原型为500 kV超高压输电线路中采用的某转角耐张塔,全塔高为54.5 m,其呼称高24 m,组成构件均为等边角钢,塔头部分共设有非对称形式的三对导线横担和一对地线支架。舞动现场调查资料显示,该输电塔横担在导线舞动作用下发生了严重破坏,而塔身构件完好无损(如图1所示)。同时,鉴于试验场地大小限制以及采用过小的缩尺比而导致的缩尺效应,本文选择包含悬挑最长中横担的塔头部分来制作输电塔节段模型(图2所示)。
基于相似理论,输电塔线体系模型除须满足与原型几何相似、刚度及质量分布相似外,还要严格保证静力和动力特性相似。对于输电塔模型,取节段模型缩尺比为1∶4。模型构件采用材料与原型相同的角钢,因此弹性模量和密度相似系数均为1∶1,其它物理量相似参数可通过量纲分析法和已确定的三个基本物理量获得(见表1中输电塔的相似参数)。对于覆冰导线,鉴于试验场地大小限制,按照1∶16的档距缩尺比制作导线模型。此外,为充分体现输电塔与导线之间的耦合效应,塔、线模型应满足一致的动力以及荷载相似参数。因此,结合输电塔节段模型的相似系数,导线张力和频率相似参数分别取为1∶16和4∶1。以导线模型档距、张力和频率为三个基本物理量,通过量纲分析确定其它物理量的相似参数(如表1中导线模型相似参数所示)。

图1 输电塔破坏照片Fig.1 Failure mode of transmission tower
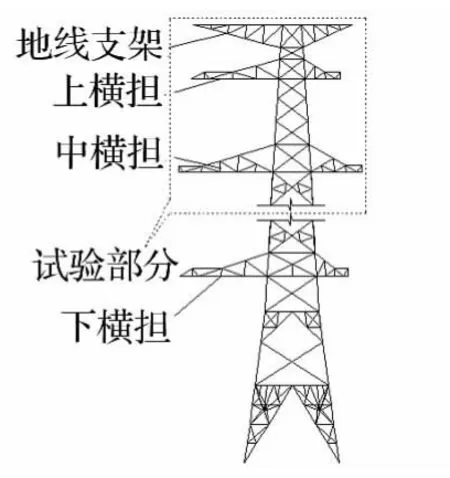
图2 输电塔节段模型示意图Fig.2 Schematic drawing of tower segmental model
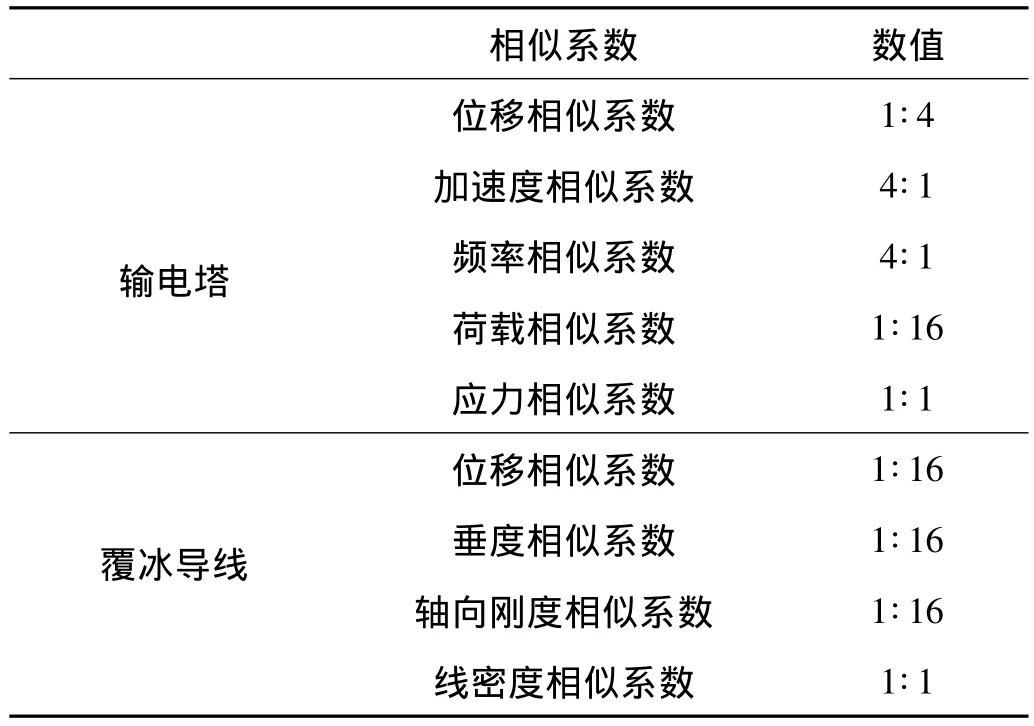
表1 输电塔线体系模型相似参数Tab.1 The similarity coefficients of transmission tower-line system
为保证输电塔节段模型与原型之间满足表1所示的动力相似参数,其边界必须是能够模拟节段模型以下塔身部分刚度的弹性支座。结合输电塔有限元模型,采用柔度法提取节段模型以下塔身部分的等效刚度,并通过对比节段模型与原型的动力特性分析结果,对支座刚度进行修正和调整,最后用模具弹簧实现弹性支座刚度的模拟。表2为输电塔原型与模型前三阶动力特性有限元计算结果的比较,可以看出二者自振频率能够较好满足表1中的频率相似系数,说明采用弹性支座能够使节段模型与全塔原型之间满足动力特性相似。图3和图4分别为加工完成的输电塔节段模型和相应的弹性支座。
输电塔的组成构件为角钢,连接方式为通过螺栓和节点板的单肢连接。为充分体现螺栓和节点板对构件传力路径和边界约束条件的影响,对应模型的螺栓和节点板均按照相似系数进行缩尺,且保证螺栓数量与节点板形状均与原型相同。另外,螺栓的预紧状态对构件受力也有着重要影响,且会受环境激励的影响而缓慢变化。然而考虑到缺乏输电塔破坏前螺栓的预紧扭矩参数,制作模型时无法确定螺栓在输电塔破坏前的预紧状态,因此难以在试验过程中模拟舞动发生时螺栓的真实松动情况。鉴于舞动试验目的在于检验杆塔构件是否发生强度破坏或者失稳,因此为防止螺栓松动对舞动试验产生干扰,本文采用双螺帽预紧的方法对模型构件的连接螺栓进行防松处理(图5所示)。
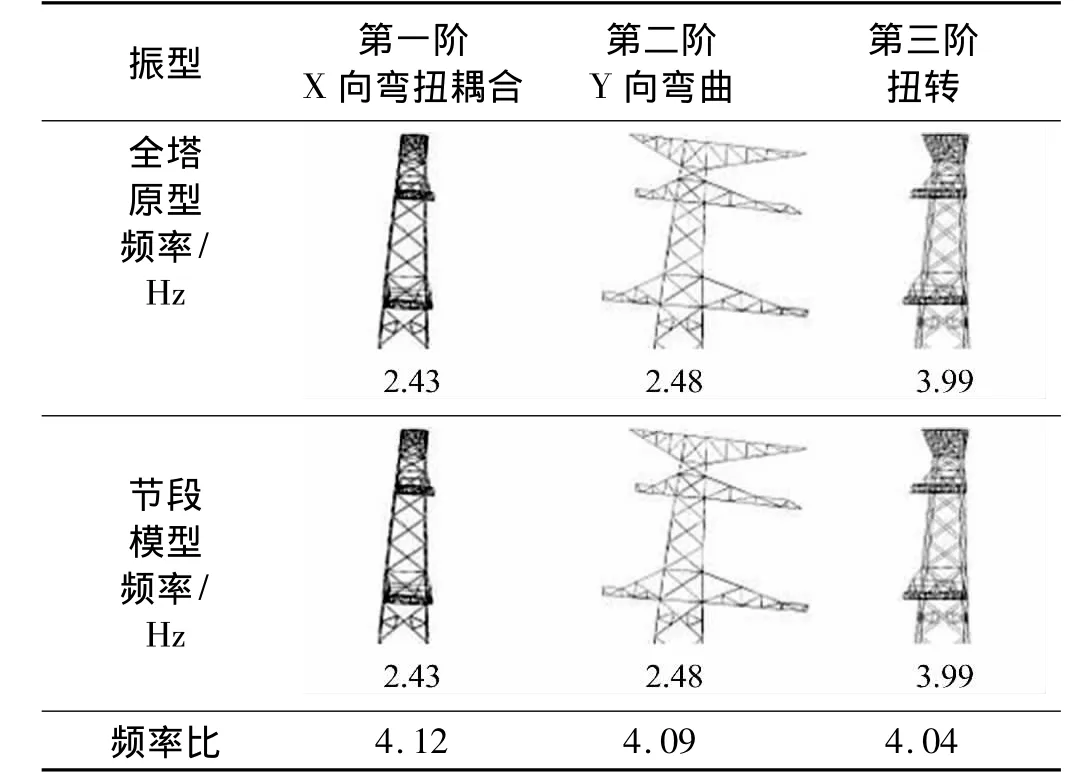
表2 节段模型与全塔原型动力特性的比较Tab.2 Comparison of dynamic characteristic between transmission tower prototype and segmental model

图3 输电塔节段模型实物照片Fig.3 Picture of tower segmental model

图4 弹性支座Fig.4 Elastic support of tower segmental model

图5 构件螺栓连接图Fig.5 Picture of bolted connection of angle steel
输电导线原型为500 kV四分裂导线,档距为244 m,其中子导线型号为LGJ-400/35。试验采用钢丝绳模拟导线轴向刚度,再辅以配重块来实现模型与原型之间的线密度相似。此外,若导线模型按照原型制成四分裂的形式,则难以实现模型与舞动试验加载装置的连接,因此本试验将四分裂覆冰导线模型等效为一根,相应导线模型的张力、线密度以及拉伸刚度均放大四倍。图6为覆冰导线模型的实物照片。

图6 覆冰导线模型Fig.6 Photo of iced conductor model
1.2 舞动试验加载装置
覆冰导线舞动以竖向振动为主,其运动轨迹为椭圆,特征频率为竖向一阶自振频率。基于上述特征,本文利用舞动试验装置,采用通过对导线跨中位置进行机械激振的方式,再现舞动时导线的动张力与运动特征。
鉴于椭圆轨迹的机械激振装置过于复杂,并考虑到导线动张力以竖向位移贡献为主,且试验关键在于重现舞动时导线的动态张拉力,本文采用圆形轨迹激振产生的动态张拉力进行替代,并对该方案进行了可行性论证工作。即通过对比导线舞动响应计算值和测试值,检验在跨中圆形轨迹激励作用下能否再现舞动时的动态张拉力以及舞动形态。
图7为舞动试验装置实物照片。舞动试验装置主要由变频器、三相异步电机以及平行四连杆机构组成。使用时首先将导线模型穿过机构连杆中部,完成导线模型的静力张拉后,根据舞动幅值和频率,分别用平四连杆机构和变频器调整装置运行半径和运动周期。进行试验时,采用逐渐增频的方式启动舞动装置,以降低在加载初期对塔线体系模型的冲击效应。

图7 舞动试验装置Fig.7 Galloping experimental equipment
以输电塔线体系原型为研究对象,计算13 m/s风速作用下的舞动响应,其中覆冰导线气动力系数采用风洞试验测试值。试验方面,利用舞动试验装置对覆冰塔线体系模型进行机械激振,竖向振幅为20 cm,最后将测得的导线动态张拉力和竖向位移按照相似关系转换至原型,并与舞动计算值进行对比。图8为导线舞动响应计算值与试验值的对比。可以看出,导线动张力的试验与计算结果吻合良好。对于跨中位移响应,由于舞动计算时作用于导线上的荷载与模型试验有所不同,因此动张力接近时,跨中位移的测试值与计算值略有差异。总体来看,在实验室条件下,用舞动试验装置对导线激振能够有效再现导线舞动产生的动张力以及相应的动态特性,说明试验装置的设计是合理有效的。在此基础上能够进行输电塔线体系舞动试验,从而对输电塔的损伤、破坏机理进行深入研究。

图8 导线舞动响应的比较Fig.8 Comparison of conductor galloping responses between test and calculation
1.3 试验布置
如图9所示,输电塔模型对应的原型为转角耐张塔,与线路走向存在73°的夹角。导线模型的一端通过拉力传感器与输电塔相连,可直接测得导线作用于输电塔上的动态张拉力;另一端通过预紧螺栓固定在反力架上。舞动试验机设置于导线模型的跨中位置。由于实际线路中输电塔横担破坏严重,而塔身无任何损伤,因此在中横担受压主材和斜材等构件的关键截面处布置应变测点(图10所示)。同时,为测得舞动时输电塔的振动响应,在塔身顶部和横担端部各布置一个加速度传感器。最后根据表1中的相似参数,将测得的输电塔线体系舞动响应转化至原型。
1.4 试验工况
结合舞动事故现场调查资料,实际线路覆冰形状为新月形,最大冰厚为20 mm,最大舞动幅值为6 m。同时,考虑到杆塔破坏时对应的导线舞动幅值尚未确定,因此为全面细致的检验塔架构件发生损伤时对应的舞动幅值,试验采用舞动幅值逐级递增的方式进行动态加载。其中舞动幅值范围取为20~54 cm(间隔2 cm),对应原型舞动幅值为3.20~8.64 m。导线模型的质量与张力参数见表3。

图9 塔线体系舞动试验布置图Fig.9 Galloping experimental system of transmission tower line

图10 横担应变测点布置Fig.10 Test points arrangement for transmission tower

表3 覆冰导线模型物理参数Tab.3 Parameters of iced-conductor model
2 试验结果与分析
试验时导线的运动形态为单个半波,以竖向一阶振型为主。输电塔绕塔身竖轴的扭转振动明显,且由于缺乏有效约束,横担交叉斜材发生了显著的面外振动。当对应导线原型舞动幅值达到实测值6 m时,全塔构件保持完好;即使舞动幅值增至8.64 m,横担和塔身部分依然保持矗立不倒,并未发生构件撕裂或失稳等现象。
图11为导线张力最大值随舞动幅值的变化规律。可以看出,舞动幅值小于5 m时,导线结构的几何非线性特征不明显,张力最大值随舞动幅值的增大而线性增加;当舞动幅值大于5 m时,张力最大值与舞动幅值之间则呈现明显的非线性关系。其中,在舞动幅值达到现场观测的6 m时,导线张力放大系数为1.92;而舞动幅值接近9 m时,张力放大系数仅增加至2.07。造成上述现象的原因在于:与导线两端固支情况的不同,对于塔线体系来说,导线内力的增大会引起输电塔挂线点位移的增加,从而减缓了张力的增长速度。该特征充分体现了塔线体系的耦合特性,表明输电塔对导线的弹性支撑作用不可忽略,在进行导线舞动响应分析时应考虑该效应的影响。
图12为输电塔加速度均方根随舞动幅值的变化规律。与导线动张力最值相似,在舞动幅值小于5 m的阶段,舞动幅值与加速度均方根之间为线性关系;而随着舞动幅值的继续增加,加速度响应与舞动幅值之间表现出一定程度的非线性特征。对比横担和塔顶的加速度响应还可发现,横担端点处的加速度响应远大于塔顶,说明在导线舞动作用下,转角耐张塔振动形式以绕塔身轴的扭转运动为主。
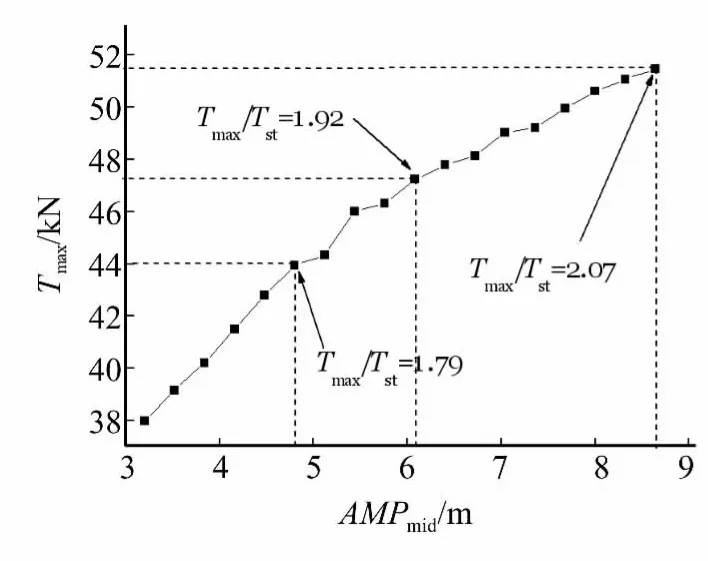
图11 张力最大值随舞动幅值的变化规律Fig.11 The peak value of dynamic tension vibrations with galloping amplitude
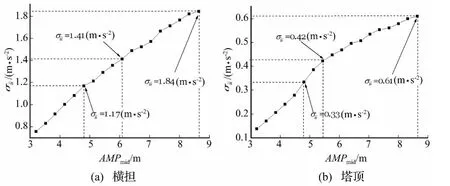
图12 输电塔加速度均方根Fig.12 The effect of galloping amplitude on acceleration of tower
导线动张力主要由横担下弦承担,而下弦层中主材A和斜材B分别为应力水平较高和计算长度最大的受压构件,属于结构的薄弱环节。因此图13给出了以上两类构件应变最大值随舞动幅值的变化规律,图例中“-”表示压应变,“+”则表示拉应变。
对比图13(a)和图13(b)可以发现,随着舞动幅值的递增,各测点应变最大值逐渐变大,且横担主材应变远大于斜材。从应力状态的角度来看,各舞动幅值下以主材A中测点2的应变值最大,其受力状态最为不利。此外,受压斜材B在中点截面上边缘处(测点7)的应力状态反而为拉,该现象表明:对于长细比较大的受压角钢,在连接偏心产生的弯矩作用下,构件截面被分为明显的受压区和受拉区。该类型连接方式会降低角钢受压稳定承载力,且在动力作用下受拉区域易发生疲劳损伤。
从图13中还可发现,当舞动幅值达到实测的6 m时,各构件控制截面的应变最大值均小于塑性应变。而在舞动幅值由6 m增加至8.64 m的过程中,仅有主材A中的测点2达到屈服状态,相应最大应变为1 273 με,说明该位置的塑性性质并不明显。同时,从试验现象来看,横担以及输电塔其它部位仍保持完好,并未发生构件撕裂、失稳甚至横担整体破坏等现象。

图13 应力最大值随舞动幅值的变化规律Fig.13 The peak value of dynamic strainvibrations with galloping amplitude
上述试验分析结果表明,覆冰导线舞动对输电塔的动力作用十分明显,但是构件承载力具有足够的安全余度,即使在舞动幅值大大超出实测值的情况下,也仅仅是在受压主材的局部位置产生了一定程度的塑性变形,而其他构件仍处于弹性工作状态,且全塔依然保持完好。说明该输电塔在导线舞动作用下的失效并非由构件材料强度和稳定承载力不足而引起的。
3 构件疲劳寿命
导线舞动时会在输电塔上作用大幅变化的动态张拉力。在该类型交变荷载作用下,构件的应力状态随时间不断变化,容易导致结构的疲劳破坏。对于钢结构来说,疲劳破坏源于材料中微裂纹的扩展,而只有压应力的部位即使出现了微裂纹,也不会继续扩展,因此在应力循环中不出现拉应力的部位可不计算疲劳。从塔线体系舞动试验结果来看,输电塔所有测点的应力状态均为始终受拉或者受压。因此,本文以舞动幅值为8.64 m时,输电塔构件最不利受拉位置(测点7)的应变测试结果为基础,采用规范[16]提供的方法计算舞动作用下的疲劳寿命:

式中:n为应力循环次数,Δσ为应力幅值。C、β为参数,根据构件和连接类型分别取3.26×1012和3。
如图14所示,舞动试验时测点7的拉应力幅Δσ=137-20=117 MPa。由式(1)可得,最不利受拉位置所能承受的应力循环次数为:

即输电塔横担至少可以承受209万次应力循环而不发生疲劳破坏。而线路现场事故调查资料显示:输电塔在舞动发生后的第三天即发生破坏。按3天计算,考虑实际线路中的舞动频率为0.367 Hz,这段时间内应力循环数至多为10万次,远小于估计的209万次,故舞动作用下该输电塔的破坏不是由构件疲劳强度不足而造成的。
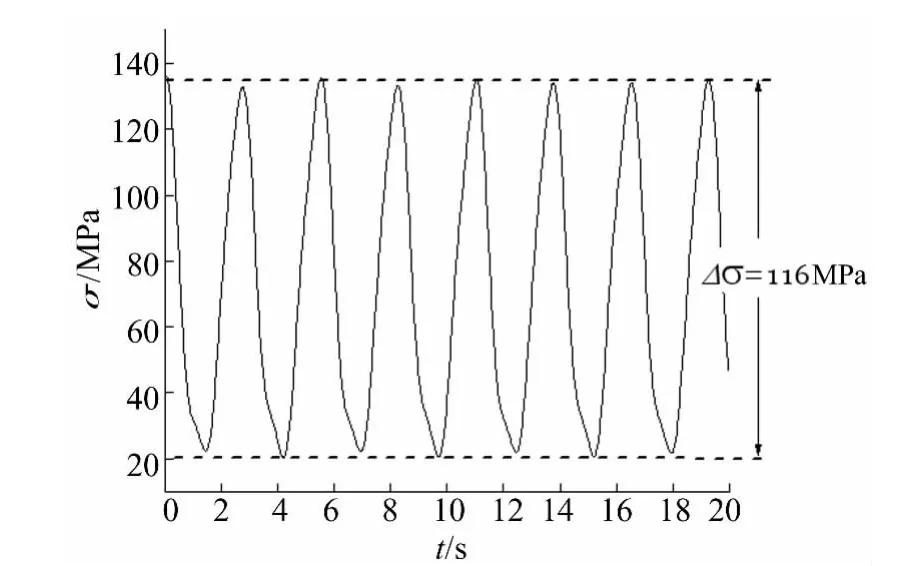
图14 最不利受拉位置的应力时程Fig.14 The stress time history of most unfavorable position
4 输电塔破坏原因分析
本次舞动试验对应原型导线舞动的最大幅值为8.64 m,远超过了实际线路损伤时的舞动幅值(6 m)。然而,在如此大幅舞动作用下,转角耐张塔仅在横担受压主材根部产生了较小的塑性应变,横担和整塔依然完好,说明构件强度和承载力不足并不是导致输电塔失效的原因。同时,结合试验测得最不利受拉位置的应力幅值,估算了舞动幅值为8.64 m时横担关键构件的疲劳寿命,结果显示构件疲劳寿命远大于线路实际舞动破坏所需要的时间,进而说明了构件疲劳强度不足亦不是导致输电塔破坏的真正原因。
综上所述,输电塔在导线舞动作用下的破坏并非是由构件承载力不足和疲劳损伤引起的,其根本原因在于导线舞动产生的大幅张拉力使构件承受较大的往复变形和内力,引起连接节点处构件间的相对位移、摩擦以及节点板与螺栓的相互挤压,逐渐造成螺栓磨损、松动、断裂甚至脱落,使主要构件的内力重新分配,导致某些构件内力过大而发生破坏,进一步造成了输电塔的失稳甚至倒塌。因此建议输电塔在实际施工过程中对螺栓进行防松动处理,以便能够更好地抵抗舞动产生的动力效应。
5 结论
本文基于大比例输电塔线体系模型以及研制的导线舞动试验加载装置,结合破坏线路的现场覆冰资料和舞动幅值,在实验室条件下进行了覆冰线路舞动事故的反演。并根据试验获得的动应力幅值,估算了输电塔在导线舞动作用下的疲劳寿命,得出以下几点结论:
(1)研制的输电塔线体系舞动试验加载装置能够有效再现导线舞动产生的动张力及其动态响应特征,因而在此基础上可以对塔线体系在舞动作用下的损伤机理和失效模式进行深层次的研究;
(2)在导线舞动作用下,输电塔振动形式以绕塔身轴的扭转运动为主。同时,由于缺乏有效约束,横担斜材面外振动明显;
(3)舞动幅值较小时,输电塔线体系舞动响应随舞动振幅的增大而线性增加;而舞动幅值较大时,舞动响应与舞动幅值之间的关系呈现一定程度的非线性特征;
(4)本文所研究的转角耐张塔在导线舞动作用下的破坏并非由构件承载力不足和疲劳损伤而造成的,导致输电塔失效根本原因在于构件连接螺栓在导线舞动产生的大幅动张力作用下失效,使主要构件的内力重新分配,致使某些构件受力过大而发生破坏,从而引发了输电塔的失稳甚至倒塌。建议在实际施工过程中对主要构件的连接螺栓采取防松动措施,以便能够更好地抵抗导线舞动所致的动效应。
[1]魏 冲 ,潘少成,唐明贵,等.500 kV输电线路舞动分析及治理[J].电力建设,2011,32(4):24-27.WEI Chong, P AN Shao-cheng, T ANG Ming-gui, e t al.Analysis and threatment of the galloping of 500 kV transmission line[J].Electric Power Construction,2011,32(4):24-27.
[2]丁锡广,陶文秋.减轻送电线路导线舞动灾害的措施[J].高电压技术,2004,30(2):54-55.DING Xi-guang,TAO Wen-qiu.Measurefor reduction of damage caused by fluttered power transmission wires[J].High Voltage Engineering,2004,30(2):54-55.
[3] 卢 明 ,孙新良,阎 东 .500 kV姚邵线舞动倒塔事故分析[J].电瓷避雷器,2008(3):1-9.LU Ming,SUN Xin-liang,YAN Dong.Cause of conductor galloping tower collapse at Yaoshao 500 kV transmission line[J].Insulators and Surge Arresters,2008(3):1 -9.
[4] A lbermani F,Kitipornchai S,Chan R W K.Failure analysis of transmission towers[J].Engineering Failure Analysis,2009(16):1922-1928.
[5] A lam M J,Santhakumar A R.Reliability analysis and fullscale testing of transmission tower[J].Journal of Structure Engineering,1996,122(3):338-44.
[6]PrasadRao N,Samuel Knight GM,Mohan SJ,et al.Studies on failure of transmission line towers intesting[J].Engineering Structures,2012(35):55 -70.
[7] Albermani F G A,Kitipornchai S.Numerical simulation of structural behaviour of transmission towers[J].Thin-walled Structures,2003(41):167-177
[8]谢 强,孙 力,张 勇.500 kV输电塔结构抗冰加固改造方法试验研究[J].中国电机工程学报,2011,31(16):108-114.XIE Qiang,SUN Li,ZHANG Yong.Experimental study on retrofitting of 500 kV transmission tower against ice load[J].Proceedings of The Chinese Society For Electrical Engineering,2011,31(16):108 -114.
[9]王 昕.覆冰导线舞动风洞试验研究及输电塔线体系舞动模拟[D].杭州:浙江大学,2011.
[10]荣志娟,张 陵.输电塔-覆冰导线耦合体系非线性动力响应分析[J].动力学与控制学报,2011,9(4):368-373.RONG Zhi-juan, ZHANG Ling. Non-linear analysis on dynamic response coupled transmission tower-iced line system[J].Journal of Dynamic And Control,2011,9(4):368-373.
[11]张 勇,严承涌,谢 强.覆冰特高压输电塔线耦联体系风致动力响应风洞试验[J].中国电机工程学报,2010,30(28):94-99.ZHANG Yong,YAN Cheng-yong,XIE Qiang.Wind tunnel test on wind-induced dynamic response of icing ultra high voltage transmission tower-line coupling system [J].Proceeding of the CSEE,2010,30(28):94-99.
[12]谢 强,严承涌,李素贞.1000 kV特高压交流输电8分裂导线动张力风洞试验分析[J].高电压技术,2010,36(7):1594-1600.XIE Qiang,YAN Cheng-yong,LI Su-zhen.Wind tunnel test analysis on dynamic tension of 1000 kV UHV eight bundled conductors[J].High Voltage Engineering,2010,36(7):1594-1600.
[13]朱宽军,付东杰,王景朝,等.架空输电线路的舞动及防治[J].电力设备,2009,9(6):8-12.ZHU Kuan-jun,FU Dong-jie,WANG Jing-chao,et al.The galloping and its preventing techniques on overhead transmission line[J].Electrical Equipment,2009,9(6):8-12.
[14]朱宽军,刘超群,任西春.架空输电线路舞动时导线动态张力分析[J].中国电力,2005,38(10):40-44.ZHU Kuan-jun,LIU Chao-qun,REN Xi-chun.Analysis on dynamic tension of conductor under transmission line galloping[J].Electric Power,2005,38(10):40 -44.
[15]张天光,孙东海,敖清诚,等.河南电网500 kV姚邵线舞动事故分析与治理措施[J].电力建设,2009(3):24-27.ZHANG Tian-guang,SUN Dong-hai,AO Qing-cheng,et al.Analysis of Henan grid’s 500 kV Yao-shao line gallop accident and its control[J].Electric Power Construction,2009(3):24-27.
[16]GB 50017-2003.钢结构设计规范[S].北京:中国计划出版社,2003.
