8 顺层滑动极限分析上限法

2013-05-24

浙江科技学院学报 2013年3期

8 顺层滑动极限分析上限法

8.1 简单平面岩质边坡极限分析上限法

8.1.1 简单平面滑动极限分析屈服机构

岩石边坡在自然界普遍存在，其典型边坡剖面如图8-1所示。为了从极限分析理论框架体系推导岩石边坡稳定系数的极限分析上限解，这里对经典的求解方法——刚体极限平衡法，进行了简单的介绍。前人从刚体极限平衡理论框架体系出发，比较系统地推导了岩石边坡平面破坏的稳定系数，其基本假定如下:

（1）滑动面的走向必须与坡面平行或接近平行；

（2）滑动面必须在边坡面出露，即滑动面的倾角必须小于坡面倾角；

（3）岩体中必须存在对干滑动阻力很小的分离面，以定出滑动的侧面边界；

（4）张裂缝垂直，其走向平行于坡面和滑面；

（5）水沿张裂缝渗入滑动面，张裂缝底与坡趾间的长度内水压力按线性变化至零（三角形分布），如图8-1所示。

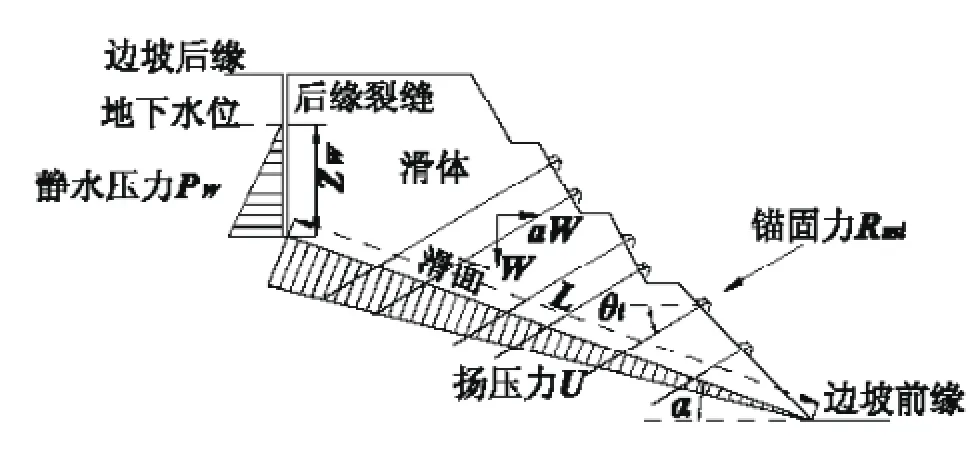
图8-1 岩质边坡稳定性分析计算模型

考虑后缘裂缝静水压力、沿滑面扬压力、水平地震惯性力、预应力锚索（杆）锚固力，根据刚体极限平衡法进行计算，可得到潜在滑动面上的稳定系数（总抗滑力和总滑动力之比）表达式为

式中：K为岩石边坡的稳定系数；W为滑体重量（kN·m-1）；a为水平地震影响系数(无量纲)；PW为后缘裂缝静水压力(kN·m-1)；U为沿滑面扬压力(kN·m-1)；Rmi为第i道预应力锚索（杆）每延米锚固力(kN·m-1)；α为滑面倾角（°）；c为滑面黏聚力（kPa）；φ为滑面内摩擦角（°）；L为滑面长度（m）。

极限分析上限定理指出，如有一种机动许可的速度场存在，则与其对应的外荷载的最小值就是极限荷载的上限，此时，该外荷载所做的功等于屈服机构（塑性变形机构）中耗散的能。对于岩质边坡，上限定理可表达为：在刚塑性假定条件下，如能找到一种机动许可的速度场，使得外荷载所做的功率等于内能耗散率，从而使岩石边坡产生沿滑面的破坏（极限状态），则相应的稳定系数为上限解。

为求取岩石边坡稳定系数上限解，需要建立一个合适的屈服机构来获得满足上限定理的机动许可速度场。对于岩石边坡平面滑动问题，应用极限分析上限法原理，可以提出如图8-2所示的屈服机构(王根龙,等，2011)。

极限分析上限法指出，当滑动体滑动时，外力所做的功率等于内力（滑面上的阻力）所消耗的功率。于是，可由滑体处于极限状态时两功率相等的条件，得到简单平面滑动屈服机构的简化虚功率方程。

式中：左侧为滑面上阻力产生的内部耗散能，右侧为外力所做的功率；Γ为岩石边坡滑面；D为作用在滑面的内能耗散；T*为极限状态外荷载；v为滑面处的土体应变速度。

8.1.2 简单平面滑动极限分析上限解

图8-2 岩石边坡平面滑动屈服破坏机构——速度场

如图8-2所示，作用在岩石边坡上的外力包括后缘裂缝静水压力、沿滑面扬压力、重力、地震惯性力、预应力锚索（杆）锚固力，计算公式分别为

（1）后缘裂缝静水压力PW

（2）沿滑面扬压力U

（3）水平地震惯性力E：

式中：a为水平地震影响系数，大小为水平地震动峰值加速度与重力加速度g的比值（无量纲），对地震烈度为Ⅶ度、Ⅷ度和Ⅸ度地区，水平地震影响系数a应分别取0.1，0.2和0.4；W为滑体重量(kN/m)。

④ 预应力锚索（杆）锚固力Rm：

式中：Rmi为第i道预应力锚索（杆）在每延米范围内提供的锚固力（kN·m-1）；Rmi1为第i道预应力锚索（杆）在每延米范围内抗拔承载力（kN·m-1）；Rmi2为第i道预应力锚索（杆）在每延米范围内由钢筋提供的抗拉承载力（kN·m-1）；Rmi3为第i道预应力锚索（杆）在每延米范围内由钢筋与砂浆提供的抗拔承载力（kN·m-1）；ξ1为锚固体与地层粘结工作条件系数，永久性锚索（杆）取1.00，临时性锚索（杆）取1.33；ξ2为锚索（杆）抗拉工作条件系数，永久性锚索（杆）取0.69，临时性锚索（杆）取0.92；ξ3为钢筋与砂浆粘结强度工作条件系数，永久性锚索（杆）取0.60，临时性锚索（杆）取0.72；fvi为第i道锚索（杆）中钢筋抗拉强度设计值（N·mm-2）；fbi为第i道锚索（杆）中钢筋与锚固砂浆粘结强度设计值（N·mm-2）；γ0为边坡工程重要性系数；γs为荷载分项系数；Di为第i道锚索（杆）锚固段直径（mm）；di为第i道锚索（杆）中钢筋的直径（mm）；Lia为第i道锚索（杆）有效锚固段长度（m）；ni为第i道锚索（杆）中钢筋的根数；Σqsik为第i道锚索（杆）和岩石摩阻比（kPa）；Six为第i道锚索（杆）水平间距（m）。

为了求得滑体上外荷载所做的功率，同时便于进行公式推导，这里将滑体自重荷载W、沿滑面扬压力U、后缘张裂缝静水压力PW、水平地震惯性力E、预应力锚索（杆）锚固力Rm共五个外力，分解后合成为水平力分量Fx和铅直力分量Fy，其计算公式分别为

这些外力在应变速度场v上所做的总功率计算公式为

滑面上的力有剪切力和法向力，其中剪切力包括两部分，一部分为黏聚力C，它是已知的，其值为cL；另一部分是摩擦力，其值为Ntanφ，它和法向力N一起，构成一个与滑面法线方向夹角为φ的合力P（图8-2）——“组合摩擦力”。这个组合摩擦力的大小通常是未知的，但它的方向是已知的，即与法线方向夹角为φ。如前所述，塑性速度v与滑面夹角为φ，这样“组合摩擦力”P与塑性速度v正交，所以P在v上所做的功为零。

通过分析可知，在计算滑面上阻力产生的内部耗散能时，只有黏聚力C在应变速度场v上做功，其计算公式为：

对于岩石边坡，按照极限分析的上限定理构建虚功率方程（8-2）时，应该满足极限破坏状态的前提条件。要使岩石边坡沿滑面过渡到极限破坏状态可以有三种方案：① 在边坡表面施加外荷载T，逐渐增加该荷载直到边坡产生破坏；② 在坡体上施加一个假想的水平体积力KhW，类似于水平地震力，逐渐增大该力直到边坡产生破坏；③ 强度折减法，即对边坡滑面的强度参数c和tanφ同时除一个折减系数K，目的使边坡达到极限破坏状态。文中采用第三种方案，经过折减后的滑面参数c'和tanφ'表达式为：

按照极限分析上限法，依照强度折减法原则，将岩石边坡外力所做的功率公式（8-9）和滑面上阻力所消耗的功率公式（8-10），代入虚功率方程（8-2）式中，消除等号两边的应变速度v项，整理后得到岩石边坡的稳定系数计算公式为

式中：φ' = Αrctan(tanφ/K)，由于上式等号右端出现了K，因此式（8-12）是稳定系数的隐式方程，需要通过迭代的算法求解。在计算时，先假设一个初始的稳定系数K，应用迭代计算直至前后两次稳定系数K值满足所要求的计算精度为止。一般来说对于满足条件的情况，迭代都是收敛的。

在岩石边坡加固工程中，当给定设计稳定系数K后，可以通过式（8-12）反算锚索（杆）预应力锚固力，其计算公式为

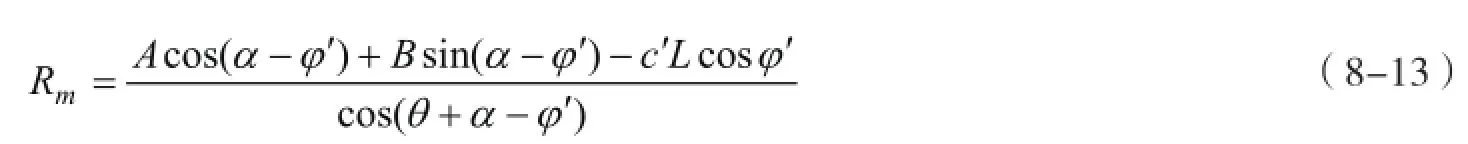
式中：

8.1.3 工程应用

1）引渠内侧边坡工程地质条件

锦屏一级水电站坝址位于四川省木里县和盐源县境内锦屏山区雅砻江大河湾洼里下游18km处普斯罗沟与手爬沟之间1.5km长的河段上，电站坝体为混凝土双曲坝，高305m，是目前世界上在建的最高混凝土拱坝。坝顶高程1 885m，蓄水位为1 880m。锦屏一级水电站是雅砻江水电站规划中的龙头水库梯级之一，装机容量3 600MW，经济效益十分显著。坝址地段属青藏高原向四川盆地过渡斜坡地带，由海拔5000～4000m降至2000m。地貌上多属侵蚀山地，地形上表现为典型的深切“V”字形峡谷。

锦屏一级水电站右岸泄洪洞引渠内侧岩质边坡（以下简称为引渠内侧边坡）位于普斯罗沟沟口上游侧。该边坡走向N62°E，倾向N28°W。边坡工程开挖高程集中在1 777 ～1 925m，共形成六级台阶，并在1 777m高程形成一个平台，属于典型的多级台阶状岩质高边坡。

引渠内侧边坡岩体中主要发育三组节理裂隙：

（2）第二组为NE向节理裂隙，产状N45～60°E/SE∠70～75°，一般长3～10m，个别大于10m，间距一般3～5m；

（3）第三组为NW向节理裂隙，产状N30～40W ° /NE∠70～80°，该组裂隙多以溶蚀裂隙形式出现，长度一般3～5m，个别5～10m，成带出现，带间间距5～10m，带内间距0.3～0.5m，充填碎块、次生黄泥，裂隙壁见溶蚀小坑孔。

2）引渠内侧边坡变形破坏模式

控制引渠内侧边坡变形破坏模式的结构面主要为fyj6断层、g8SZ-1，gyj7和gyj2层间挤压错动带。这四条结构面规模为Ⅲ级。值得注意的是，断层fyj6产状与第二组节理裂隙产状一致，层间挤压错动带g8SZ-1，gyj7和gyj2产状与第一组层面裂隙产状一致。

（1）fyj6断层

产状 N40～50°E/SE∠70～75°，根据层面裂隙发生的一系列牵引现象，分析认为fyj6为正断层。该断层出露于普斯罗沟沟口上游壁（图8-3），主要由碎裂岩、糜棱岩、重结晶的方解石脉组成，夹少量黄褐色泥，局部断层带物质后期被地下水带走，形成2～3cm裂隙。上、下盘主断面明显，有强锈，见擦痕。断层上盘影响带宽约5m，呈碎裂岩体，同向裂隙密集发育，间距10～30cm，裂面重度锈染，岩体强风化（见图8-4）。fyj6断层构成了边坡后缘拉裂缝。

图8-3 引渠内侧边坡后缘fyj6断层（镜向SW）

图8-4 fyj6断层破碎带（镜向SW）

（2）g8SZ-1层间挤压错动带

产状N40～60°E/NW∠30～50°，破碎带厚约5～20cm，主要由黄色、黑色糜棱岩、碎裂岩组成，局部见绿片岩强风化形成的黄泥，绿片岩、糜棱岩遇水易软化泥化，性状差，根据产状推测g8SZ-1可能在引渠内侧开挖边坡坡脚（约1 780m高程）附近出露，构成控制引渠内侧边坡顺层滑动的第一个底滑面。

（3）gyj7层间挤压错动带

产状N55～60°E/NW∠30～35°，由6条组成，间距1.5～2m，单条宽一般0.5～2cm，主要由强风化绿片岩组成，在上下盘面可见少量糜棱岩，遇水软化泥化。该组挤压带在工程边坡的1 800～1 815m高程附近出露，构成了控制引渠内侧边坡顺层滑动的第二个底滑面。

（4）gyj2层间挤压错动带

产状同gyj7层间挤压错动带，主要由绿片岩、糜棱岩组成，厚度较大，局部达50cm，带内绿片岩已强风化，遇水软化泥化。地表观测可见监测交通洞洞口下方有一个顺层发育的大光面，推测为gyj2层间挤压错动带上部岩体沿该挤压带滑塌后形成，因此总体看来gyj2延伸较长，性状变化较大。该层间挤压错动带在工程边坡的1 890～1 900m高程出露，构成了控制引渠内侧边坡顺层滑动的第三个底滑面。

综合分析认为，引渠内侧边坡岩体结构为层状结构，根据边坡与岩层产状关系，该边坡为顺层边坡，其变形破坏模式为典型顺层滑动（见图8-5）。边界条件为：① fyj6断层构成了边坡后缘拉裂缝；② g8SZ-1，gyj7和gyj2层间挤压错动带构成控制引渠内侧边坡顺层滑动的三个底部滑裂面。

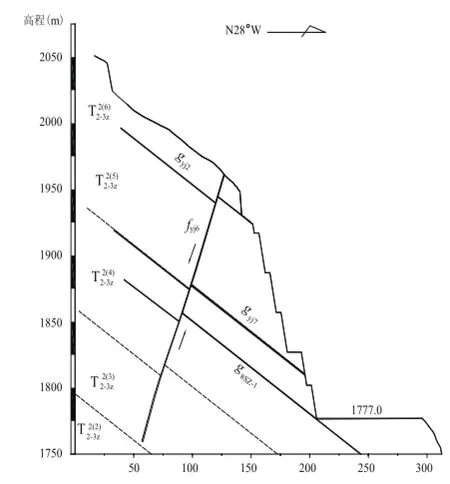
图8-5 引渠内侧边坡工程地质剖面

3）极限分析上限法分析计算

锦屏一级水电站右岸泄洪洞引渠内侧边坡为典型顺层滑动变形破坏模式。从计算剖面（见图8-5）分析可知，可能的滑面组合有三种。考虑到结构面的连通率、起伏差、带内物质成分变化等因素，结构面力学参数取值见表8-1。

分析计算过程中考虑不同的工况条件，在考虑暴雨工况时，计算后缘张裂缝静水压力，按照后缘拉裂面充水1/3计算；在考虑地震作用力时，水平地震影响系数参照坝区基本地震烈度（Ⅶ度），取值为0.1；当考虑预应力锚索加固工况时，每延米锚固力的选择因加固范围不同而异，滑面组合1的锚固力取15000kN·m-1，滑面组合2的锚固力取10000kN·m-1，滑面组合3的锚固力取1000kN·m-1。

采用刚体极限平衡法和极限分析上限法，对引渠内侧边坡进行了稳定性计算。通过编写计算机程序进行分析计算，考虑不同的组合滑面和工况，结果显示（表8-2），刚体极限平衡法与文中提出的极限分析上限法计算结果最大绝对误差均小于0.035。

表8-1 结构面力学参数

表8-2 施工期边坡稳定性计算结果

* 绝对误差是指刚体极限平衡法计算得到的稳定系数与极限分析上限法计算得到的稳定系数的差值。

8.2 顺层岩质边坡极限分析上限法

顺层岩质边坡是工程实践中经常遇到也是较容易产生破坏的一类边坡。顺层边坡是指岩层走向、倾向与边坡走向、倾向一致或接近的边坡，其破坏主要表现为剪切滑动和溃曲。

顺层边坡的剪切滑动破坏发生较多，如京珠高速公路韶关段K98工点路堑为顺层边坡，1999年11月12边坡开挖，发生沿软弱层面滑动的顺层滑坡，影响工期15天（叶志华，等，2006）重庆万州吉安于2004年9月5日发生顺层滑坡，滑坡面积0.7km2，体积约7.6×106m3，滑坡摧毁了当地一个重要的集镇、公路和在建的高速公路（李守定，等，2005）。剪切滑动的顺层岩质边坡稳定性分析通常采用刚体极限平衡法和数值模拟方法（如有限元、离散元等）（龚文慧，等，2006；李亮辉，等，2004；冯君，等，2005），而从极限分析上限法原理求解顺层岩质边坡的稳定系数则是一项新的研究课题，也是本章节的研究重点。

图8-6所示，为顺层岩质边坡剪切滑移的两种主要模式。其中，图8-6（a）为厚层硬岩沿薄层软岩剪切滑移模式，图8-6（b）为厚层硬岩沿层面剪切滑移模式。对于此类顺层岩质边坡的稳定性分析评价，通常采用刚体极限平衡法，但以下的几个问题应该引起注意：

（1）顺层岩质边坡的剪切滑移可以形成多个可能的滑动面，这些滑动面将滑体分为多个层状岩体；

（2）顺层岩质边坡各滑体的运动速度可以不同，各滑体的剪切滑移存在相互错动现象；

（3）厚层硬岩可以被视为刚体，但薄层软岩和层面并非是刚体，而应该为塑性体。

尽管刚体极限平衡法以其公式简单、计算方便而被许多工程所应用，但以上的三点刚体极限平衡法均不能得到合理的考虑。据此分析，刚体极限平衡法用来评价顺层岩质边坡的剪切滑动问题存在一定缺陷。

图8-6 顺层岩质边坡地质模型

极限分析上限法指出，当滑动体滑动时，外力所做的功率等于内力（滑面上的阻力）所消耗的功率。于是，可由滑体处于极限状态时两功率相等的条件，得到顺层岩质边坡剪切滑动的虚功率方程。

式中：左侧为顺层岩质边坡各滑面的内部耗散能；右侧为各滑体在外力作用下产生的外力功率；Di为第i个滑面（带）的内能耗散；Fi为作用于第i个滑体的外力（如自重、地震惯性力）；vi为第i个滑面(带)处的土体应变速度。

8.2.1 顺层滑动模式

图8-7所示为顺层岩质边坡的双滑面几何模型（王根龙，等，2010），滑面1和滑面2的厚度分别为h1和h2，长度分别为l1和l2，岩层倾角为α，边坡坡角为θ。以图8-7所示的双滑面顺层岩质边坡为例，其可能发生的剪切破坏模式包括三类，分别为局部滑动模式Ⅰ、整体滑动模式Ⅱ和滑体错动模式Ⅲ。

图8-7 顺层岩质边坡几何模型

局部滑动模式Ⅰ代表滑体1沿滑面1发生剪切滑动破坏，而滑面1下部岩体不发生滑动破坏。整体滑动模式Ⅱ代表滑体1和滑体2整体沿滑面2产生剪切破坏，且滑面1不发生错动。滑体错动模式Ⅲ代表滑体1和滑体2产生错动滑动破坏，根据错动关系又可以分为两个亚类：Ⅲ-1模式，代表滑体1相对滑体2向下错动；Ⅲ-2模式，代表滑体2相对滑体1向下错动。

在运用极限分析上限法原理推导这三个模式的稳定系数公式时，应满足三个条件：① 硬岩为刚性体（如厚层灰岩、砂岩等），软岩为塑性区（如页岩、泥岩），另外层面和黏土物质组成的软弱夹层也被定义为塑性区；② 滑面为速度间断面（塑性变形区），速度在滑面发生急剧而连续的变化；③ 不同滑面法向速度不变，同一滑面切向速度按线性变化。

8.2.2 局部滑动模式Ⅰ和整体滑动模式Ⅱ

局部滑动模式Ⅰ的滑面1上有剪切力和法向力（见图8-8），其中剪切力包括两部分，一部分为黏聚力C，它是已知的，其值为c1l1；另一部分是摩擦力，其值为Ntanφ1，它和法向力N一起，构成一个与滑面法线方向夹角为φ1的合力P——组合摩擦力。这个组合摩擦力的大小通常是未知的，但它的方向是已知的，即与法线方向夹角为φ1。如前所述，塑性速度v与滑面夹角为φ1，这样组合摩擦力P与塑性应变速度v正交，所以P在v上所做的功为零。

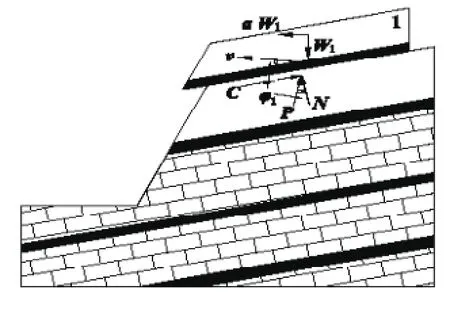
图8-8 局部滑动模式Ⅰ

通过分析可知，在计算滑面上阻力产生的内部耗散能时，只有黏聚力C在应变速度场v上产生内能耗散，其计算公式为

式中：D内为滑面1产生的内能耗散；c1为滑面1的黏聚力；φ1为滑面1的内摩擦角；l1为滑面1的长度；v1为滑面1的塑性应变速度。

作用于滑体1上的外力包括自重和水平地震惯性力两部分，它们在应变速度场v上所做的外力功率计算公式为

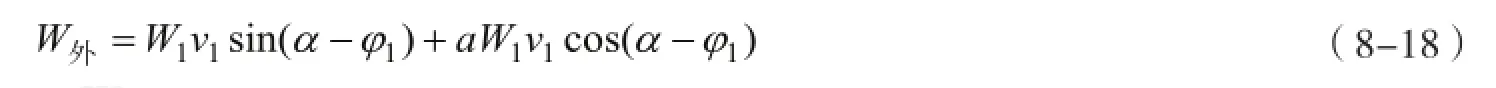
式中：W外为滑体1在应变速度场v1上所做的外功率；W1为滑体1的重量；α为滑面的倾角；a为水平地震影响系数；其他符号同上。

在应用虚功率方程（8-15）时，应该注意两个问题：其一是要满足极限状态的条件，这一点可以通过强度折减法得以实现；其二是要求外力功率为正的条件。当α ＞ φ时，外力功率为正的条件显然满足，而当α ＜ φ或α = φ时，可能存在外力功率为负的情况，此时虚功率方程将不能够成立。如果出现外力功率为负的情况，可以终止计算，并认为边坡衡为稳定状态。在以下的公式推导过程中，这两个问题也必须得到考虑。

联立式（8-15）～式（8-18），经过整理，可以消掉所有的应变速度项，最终得到顺层岩质边坡局部滑动模式Ⅰ的稳定系数极限分析上限法表达式为

式中：

对于顺层岩质边坡整体滑动模式Ⅱ（图8-9），由于滑体1和滑体2以相同的速度发生整体运动，因此滑面1不存在剪切错动，也就没有产生内能耗散，所以内能耗散仅产生于滑面2上。同样，可以推导得到顺层岩质边坡整体滑动模式Ⅱ的稳定系数极限分析上限法表达式为

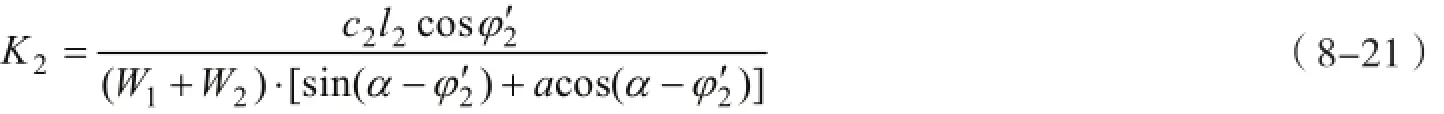
式中：c2为滑面2的黏聚力；φ2为滑面2的内摩擦角；l2为滑面2的长度；W2为滑体2的重量；其他符号同上。且有

图8-9 整体滑动模式II

8.2.3 滑体错动模式Ⅲ

顺层岩质边坡的滑体错动模式Ⅲ，存在两种不同的滑体相互错动方式，这里以Ⅲ-1模式（上部滑体突出，见图8-10）为例进行公式推导。滑面2剪切滑动产生的内能耗散D内-2计算公式为

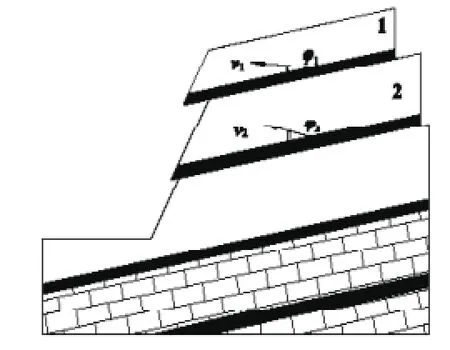
图8-10 滑体错动模式Ⅲ-1

由于滑体1相对于滑体2有向下突出的滑动趋势，所以有v1＞ v2。根据不同滑面法向速度不变的条件，可以得到v1和v2的关系式

为了便于后续公式推导的需要，这里将v2表示为v1的代数表达式

根据滑面层间错动速度（切向速度）线性变化的条件可知，滑面1相对滑体2的速度Δv为：

进一步可以得到滑面1产生的内能耗散计算公式为

滑体1和滑体2在自重力和水平地震惯性力作用下，分别在相应的应变速度场v1和v2上所做的外力功率W外-1和W外-2计算公式为：

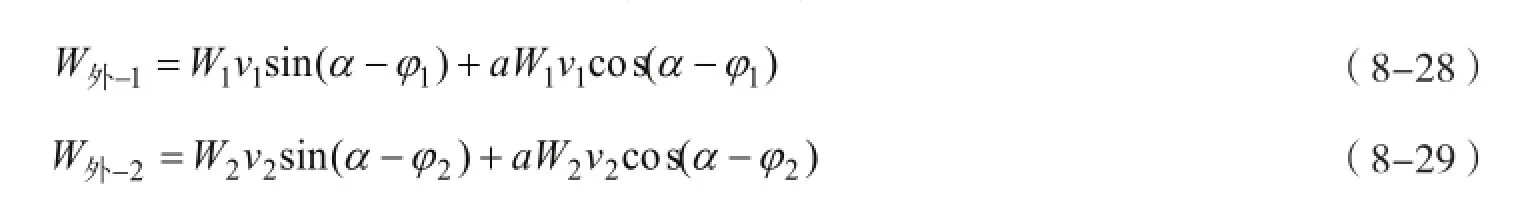
联立式（8-15）、式（8-16）、式（8-23）、式(8-25)、式（8-27）、式（8-28）和式（8-29），消掉所有应变速度项后，整理可以得到滑体错动模式Ⅲ-1的极限分析上限法稳定系数计算公式为

式中：

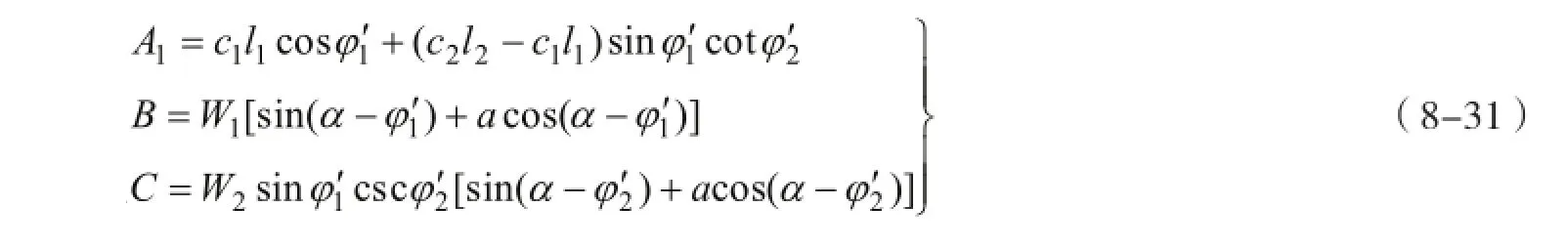
且有

对于顺层岩质边坡滑体错动模式Ⅲ-2（下部滑体挤出，见图8-11），由于滑体2相对于滑体1有向外挤出变形破坏的趋势，所以有v2＞ v1。此时，滑面1相对于滑体2的速度Δv为

进一步可以得到滑面1产生的内能耗散1-内D为

按照推导式（8-30）的方法，同理可以得到岩质边坡滑体错动模式Ⅲ-2的极限分析上限法稳定系数计算公式为

式中：

且有

在采用极限分析上限法推导顺层岩质边坡稳定系数计算公式时（包括局部滑动、整体滑动和滑体错动三种模式），两端均有稳定系数K，因此是稳定系数的隐式方程，需要通过迭代的计算方法求解。在计算时，先假设一个初始的稳定系数K，应用迭代计算直至前后两次稳定系数K值满足所要求的计算精度为止。一般来说对于满足条件的情况，迭代都是收敛的。

图8-11 滑体错动模式Ⅲ-2

8.3 顺层岩质边坡稳定性极限分析算例

渝怀线DK385+470～DK385+700段为典型的顺层岩质边坡（白云峰，2005）（图8-12）。该段边坡地层岩性为寒武系中统平井组（ε2p）厚层白云质灰岩夹泥质灰岩，岩层产状85°∠24°。岩层中共有两层溶蚀性泥灰岩，自上而下分别编号为滑面1和滑面2，位于地表以下5m和8m处，厚度分别为8cm和20cm。被滑面1和滑面2隔离的滑体1和滑体2单宽重量分别为1 1097kN·m-1和6 658 kN·m-1。距坡缘81m的后缘有明显的张裂缝。边坡开挖到15m，发现第二层溶蚀性泥灰岩下覆岩体较为稳定，但上部岩体具有滑移的迹象，需要通过稳定性分析为进一步边坡加固治理提供依据。

该边坡为典型的顺层岩质双层滑面型边坡，若采用规范推荐的刚体极限平衡法，则无法考虑中间滑面1对边坡稳定性的影响，而采用文中的方法则可以克服这一缺陷，使稳定性评价更加趋于合理。计算用到的滑面基本参数详见表8-3。

图8-12 渝怀线顺层岩质边坡工程地质剖面

表8-3 渝怀线顺层岩质边坡上限法分析滑面参数

首先，对滑体1的稳定性做出判断，将数据代入局部滑动模式Ⅰ的极限分析上限法稳定系数计算公式（8-19）中，得到天然状态下稳定系数K1=0.999，说明滑体1处于不稳定状态。然后，将基本参数带入整体滑动模式Ⅱ的的极限分析上限法稳定系数计算公式（8-21）中，得到天然状态下稳定系数K2=1.109，说明不考虑滑面1的影响时，滑体2处于稳定状态。最后，将基本参数代入滑体错动模式Ⅲ-1（因为φ1＜ φ2，所以v1＞ v2）的极限分析上限法稳定系数计算公式（8-30）中，得到极限分析上限法的稳定系数K31=0.963，说明滑体1和2均处于不稳定状态。由于模式Ⅲ-1考虑了滑面1的影响，因此计算结果要比模式Ⅱ小。笔者认为，这样的稳定系数计算结果更加符合客观规律，对指导生产具有实际的意义。

当考虑水平地震作用力时，可以得到更为详细的极限分析上限法稳定系数计算结果，详见表8-4。分析可知，当地震烈度为Ⅶ度时（相应水平地震影响系数Kc=0.1），不管用哪个模式，都可以得到滑体1和滑体2不稳定的结论，可见地震作用对该边坡稳定性影响较大。

采用规范推荐的刚体极限平衡法，针对局部滑动模式Ⅰ和整体滑动模式Ⅱ，其计算结果和极限分析上限法稳定系数计算结果完全一致（见表8-5），但对于滑体错动模式Ⅲ-1，刚体极限平衡法显然是不适用的，因为它不能考虑层间错动的影响，所以不能进行计算。此时文中的方法就显示出了其可以考虑中间滑面的优点。结果表明，考虑中间滑面的不利影响，极限分析上限法稳定系数要比刚体极限平衡法稳定系数计算结果小15%。因此，采用刚体极限平衡法解决顺层岩质边坡稳定性问题，有时会夸大边坡的稳定性，从而给以后工程的运行留下事故隐患。

表8-4 极限分析上限法稳定系数计算结果

表8-5 两种方法计算结果对比

8.4 岩质边坡后缘张裂缝发生位置的预测方法

岩质边坡发生滑坡和崩塌之前，总是伴随着一些变形现象，最明显的就是后缘或顶部产生的张裂缝（蒲春平，等，2006；高永涛，等，2002；金培杰，2003）。对于公路、铁路沿线的岩质边坡，如果能在施工期间和运营期间严密监测后缘张裂缝的发生位置和变形情况，就能对防止崩塌和滑坡灾害起到积极作用。预测后缘张裂缝位置的作用有三点：① 有助于合理布置边坡变形监测点；② 可以初步确定产生滑坡的后缘边界；③ 对于设置顶部截水沟位置具有指导意义。

预测岩质边坡后缘张裂缝发生位置的方法一般采用数值模拟，这种方法的重点是找到坡体后缘的张应力区，如果张应力大于岩石单轴抗拉强度，则产生张裂缝。但其缺点是建模复杂，并且应用起来比较困难。这里运用极限分析方法，通过潜在滑体处于极限状态时两功率相等的条件，得出了极限分析稳定系数和张裂缝发生位置的函数关系。

以图8-13所示岩质边坡为预测模型（王根龙，等，2007），边坡高度为H，坡度为θ。边坡的变形破坏主要受结构面控制，结构面倾角为α，结构面黏聚力为c，内摩擦角为φ。顶部张裂缝距坡肩距离为b。受顶部张裂缝的切割，有效滑面长度为L（Hoek 和 Bray，1983）。

根据图8-13所示几何关系，可以推导得到用θ，α，H和b表示的有效滑面长度及滑体重量计算公式为

式中：γ为岩石的重度，单位kN·m-3。当岩质边坡确定后，几何参数H，θ和α就是已知量，而b是待求量。因此，式（8-38）和式（8-39）可以简记为b的函数。

后缘张裂缝b的最小取值为零，位于坡肩位置；最大取值为bmax=H(1/tanα-1/tanθ)，位于外倾结构面在坡顶的出露位置。

滑面（结构面）上的力有剪切力和法向力，其中剪切力包括两部分，一部分为黏聚力C，它是已知的，其值为cL；另一部分是摩擦力，其值为Ntanφ，它和法向力N一起，构成一个与滑面法线方向夹角为φ的合力P（图8-14）——“组合摩擦力”。这个组合摩擦力的大小通常是未知的，但它的方向是已知的，即与法线方向夹角为φ。如前所述，塑性速度v与滑面夹角为φ，这样组合摩擦力P与塑性速度v正交，所以P在v上所做的功率为零。通过分析可知，在计算滑面上阻力产生的内耗散能时，只有黏聚力C在应变速度场v上做功，其计算公式为

边坡在自重作用下沿应变速度v所做的外力功率为

图8-13 边坡后缘张裂缝预测模型

图8-14 计算分析法计算模型

对于图8-13所示的预测模型，其虚功率方程式为W外=D内。但虚功率方程成立的基本条件是极限状态。要使预测模型的岩质边坡达到极限状态，一般采用强度折减法。具体做法是对边坡滑面的强度参数c和tanφ同时除一个折减系数K（稳定系数），经过折减后的滑面参数c'和tanφ'表达式为

联立式（8-42）、式（8-43）和式（8-44），消掉所有应变速度项，整理后得到滑体稳定系数表达式为

式中：K为能量法稳定系数；φ' 为极限状态时的内摩擦角折减值，其计算公式为

将式（8-40）和式（8-41）代入式（8-45）中，即可以得到用于预测岩质边坡后缘张裂缝b值的计算公式，其表达式为

当计算后缘张裂缝位置b时，需要在b的取值范围内按照一定的间距逐一取值，当稳定系数最小时，此时对应的b即为待求值。但需要注意的是，上式需要通过迭代的计算方法进行求解，计算精度可以取为10-6。一般来说，对于满足条件的情况，迭代都是收敛的。

某一岩质边坡，坡高H=30.5m，坡角θ=60°，坡内有一外倾结构面，结构面倾角α=30°，岩石重度γ=25.6kN·m-3。结构面的黏聚力c=48.6kPa，内摩擦角φ=28°。以下通过文中方法对坡顶产生张裂缝的位置进行分析预测。

首先计算b的取值范围，得到b的取值区间为[0，35.2]。以1m为间距，分别将b=0，b=1，b=2，…，b=35，代入式（8-47），可以得到一系列对应的极限分析稳定系数K，计算结果见表8-6。为了更为直观的获得后缘张裂缝与能量法稳定系数的关系，这里对这些离散的点进行了拟合，得到图8-15所示曲线。从曲线的最低点可以看出，b=13时，边坡的稳定系数达到了最小，从而得出结论：距离边坡肩13m的地方是最有可能出现张裂缝的位置。但由于地质体条件的复杂性和众多不确定性因素的影响，后缘张裂缝位置b较为合理的结果应该是13m左右。