组合式航天器概念及构型变换最优脉冲控制

田爱平 宝音贺西 李俊峰

1.海军航空工程学院飞行器工程系，烟台 264001 2.清华大学航天航空学院，北京 100084

在航天系统中，不确定性因素大量存在，如技术不确定性、环境不确定性、用户的变化、需求的变更和设备的更新等。对于一个航天器系统来说，其灵活性、可靠性的优劣主要表现在对这些不确定性因素的应对能力上。提供优良的性能以及在面对上述不确定因素时应具有较高的可靠性，是航天器系统同时要达到的目标。增大安全系数、增加冗余备份以及增设其他能提高可靠性的设备是应对技术以及环境风险，提高航天器可靠性的通常做法。冗余元件的增加使系统的复杂程度更高，系统的规模、开发成本以及开发周期都会随之增加。大型、复杂的航天器系统是高度综合的，其研发周期往往较长，其效能很难有伸缩的余地，往往只允许在初始设计阶段进行变更，且较小的变更需求都有可能使投入成本急剧增加。另外，面对在轨失效、元件老化等问题时，传统航天器系统也表现出较差的适应能力。为解决传统航天器系统研发中的这些问题，国外上世纪70年代开始探索新的航天器设计思想。

NASA从上个世纪70年代就开始了多任务模块化航天器的研究，称为MMS(Multi-mission Modular Spacecraft)[1]。Larry[2]提出一种模块化航天器结构，各模块可以根据需要进行最大程度的堆叠或者最大程度的展开。Bethscheider[3]提出一种包含多个模块化卫星的卫星群概念，各个不同模块具有不同的主要功能，模块之间有通信以及数据交互，每一个模块卫星都可以进行独立的控制，可以进行模块的增减或模块的新旧更替。Brown等[4-7]针对航天器系统在研制开发运行的全寿命周期中所遇到的种种不确定性，提出一种分体式航天器系统(Fractionated Spacecraft)概念。SMART Bus[8]计划开发出标准化的小卫星模块，通过模块的组合来快速制作微小卫星。日本东京大学领衔开发的PETSAT(Panel Extension Satellite)[9]由独立设计的即插即用的功能模块组成功能完整的航天器。MIT的SWARM(Self-Assembling Wireless Autonomous Reconfigurable Modules)[10-11]项目主要研究小型化航天器系统的模块化、无线通信和标准接口。模块化、可重组高能技术MRHE(Modular, Reconfigurable, High-Energy)[12]研究空间太阳能电站，模块化的结构组装是其中一项重要技术。

上述各种思想对航天器系统的开发提供了较多思路，但不同的空间任务要求航天器系统具备不同的空间构型，单一的构型对完成复杂的空间任务都具有局限性。本文在前人的基础上，提出了一种灵活性，可靠性更好的组合式航天器概念。利用相对运动动力学方程，针对组合式航天器空间任务构型变换，设计了给定机动时间的、以燃料消耗最少为目标的优化脉冲控制方法，并给出了仿真算例。

1 组合式航天器概念

组合式航天器是由若干结构上具有一定“同构性”，功能上相互独立或相近的较小的航天器组成的空间飞行器。根据任务需求，子航天器可以独立工作，也可以协同工作；可在轨灵活组合或分离，以完成特定的、复杂的空间任务。这个概念继承了模块化航天器的模块化和接口标准化思想，借鉴了在轨自主组装任务构型的思想，其主要关键技术有：

1)模块化设计。这里的模块化不仅指将航天器的各不同功能部分分割成模块的形式，还指组合式航天器系统中能独立工作也能相互间协同工作的各子航天器所表现出来的形式上的模块化。各个子航天器本身是模块化组装的结果，同时又是协同工作时组合式航天器大型系统的一个模块单元。采用模块化设计的组合式航天器系统能够提供后期设计能力。这些操作对应系统灵活性的不同表现：可维护性、可缩放性、可重构性。不管是根据在轨性能需求，进行适当调整的能力，还是应对元件在轨失效、元件老化等问题的能力，都比传统航天器有较大改善。

2)标准化接口。组合式航天器模块化设计中，应把航天器的各个功能模块及各子航天器模块标准化，保证接口的一致性，这样可以缩短研发周期和降低开发成本。每一个模块都可以在不同的研制部门各自独立设计，打破了目前整体设计，分系统相互制约，反复迭代的复杂设计模式。同时，通过模块的可更换性，把以往的故障串联式转化为故障并联式，将风险分散到各个功能模块上。另外，这种标准化设计也可以给航天器的建造提供一种可扩展和可收缩的弹性，从而保证可以根据需要在设计的中途调整航天器的规模，克服以往整体设计没有弹性的缺点。各子航天器的标准对接接口类型可以包括机械联接、能量传输、数据传输等。

3)灵活的运行模式。组合式航天器系统根据空间任务的不同，可独立运行，也可协同工作。每一个子航天器上的有效载荷，如各类敏感器，其分辨率和其孔径有关，孔径越大，分辨率越高。因此，可以由多个小型传感器组成大型传感器，或融合多个小型传感器信息得到更多更精确的信息，在中心子航天器上形成传感器组合。系统的软、硬件升级可以通过地面发射升级的子航天器来完成。组合式航天器采用的运行模式在很大程度上取决于相应的空间任务构型。

4)可变的空间任务构型。航天器的构型根据空间任务的不同而可组可分是组合式航天器的主要思想。其空间飞行状态主要有2种：编队飞行状态和整体组合飞行状态。组合式航天器的各子航天器可以按照空间任务的预定计划，形成编队飞行或组合体。根据任务的进一步需要，还可以实现空间任务构型的变换。这种通过相互间协作实现多个航天器功能重组的组合式航天器系统，与传统的独立航天器系统相比，功能上已发生了巨大变化。其不仅能够完成传统的空间任务，而且可以实现单个航天器无法实现的功能，如大范围立体成像、空间长基线干涉测量、地面目标的立体长时间不间断跟踪观测等。不同的空间任务可能需要组合式航天器系统的不同构型，因此，构型变换能力对于不同空间任务的有效实现具有重要意义。对于整体组合状态，多个子航天器可以组合为各种不同的几何形状，如图1所示。对于编队飞行状态，多个子航天器可以从某一种编队构型变换到另一种编队构型，如图2所示。

图1 组合式航天器整体构型变换

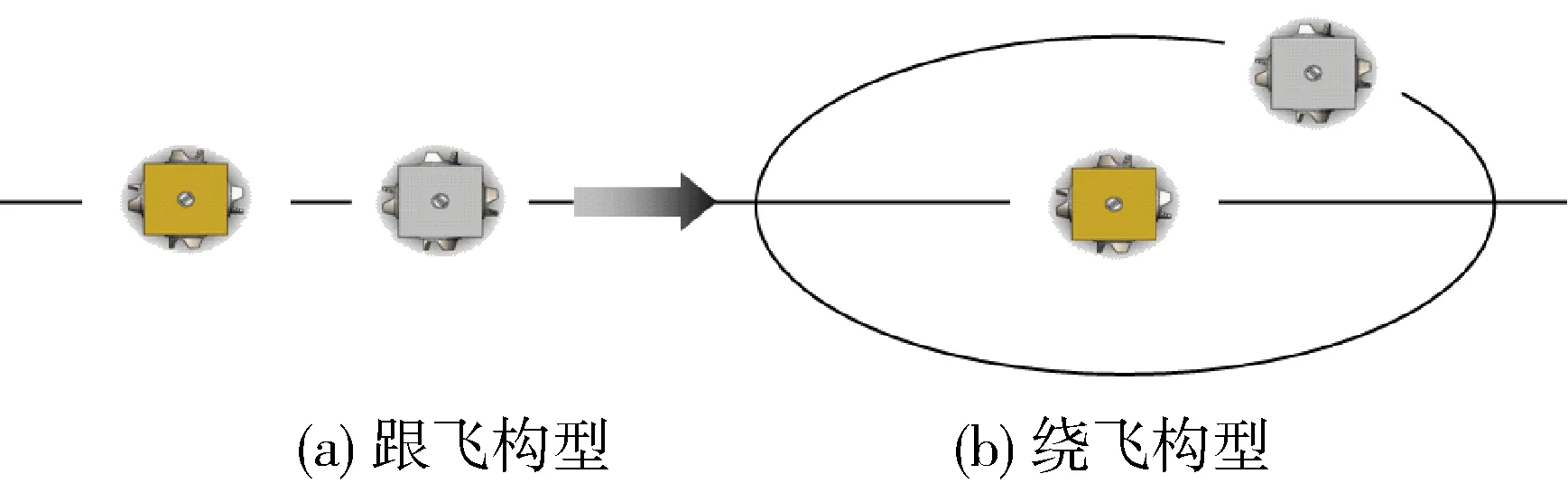
图2 组合式航天器编队飞行状态构型变换

2 组合式航天器空间构型变换的最优脉冲控制

组合式航天器的构型变换能力是组合式航天器优越性的具体体现之一，也是完成各种复杂空间任务的必要保证。组合式航天器的构型变换在本质上和航天器编队的队形设计与变换[13]以及航天器的空间交会[14-15]是相似的。对于单个子航天器来说就是轨道机动问题。在航天任务中，航天器所携带的燃料一般都是有限的、不可再生的，在完成各种航天任务的过程中，尽可能的节省燃料必然成为一项非常重要的工程问题[16]。本节针对组合式航天器系统的这种构型变换过程，进行动力学分析，给出一种基于线性规划方法的脉冲最优控制方法。给定机动时间的编队飞行构型变换问题一般可以抽象为一个参数优化问题。组合式航天器构型变换问题可描述为：在给定的机动时间内，针对组合式航天器初始以及目标构型，以消耗燃料最少为优化目标，以执行机构的能力、避免发生碰撞等为约束条件，生成最优机动轨迹。

脉冲发动机能在较大范围内提供推力、控制灵活、工程上易于实现，是轨道机动的传统方法。本文即采用脉冲方式进行轨道机动控制，完成构型变换过程。

2.1 坐标系

如图3所示，XECIYECIZECI，xyz分别为地心赤道坐标系、参考体轨道坐标系。

图3 地心赤道坐标系与轨道坐标系

2.2 相对运动动力学方程

对于组合式航天器的整体组合构型变换过程，用相对状态量来描述较为方便。设研究对象为两子航天器，分别称为主、从航天器，并假设主航天器运行于地球中心引力场的圆轨道上，忽略各种轨道摄动的影响。若不施加控制，并忽略高阶小量，可以得到在Hill坐标系下表示的从航天器相对于主航天器的相对运动动力学方程(常称Hill或C-W方程[17])为：

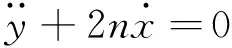
(1)

其中：n为参考轨道角速率，x，y，z为从航天器在参考轨道坐标系中的坐标。此方程的解析解为式(2)所示。

(2)

C-W方程在推导过程中采用了近似处理，其误差的量级和相对距离有关。本文以圆轨道为参考轨道，探讨组合式航天器的构型变换问题，相对运动尺寸较小且操作持续时间较短，用C-W方程具有很好的近似。

2.3 组合式航天器构型变换控制方程

将方程(1)重写成状态方程形式，并施加控制，则系统控制方程可表示为如下矩阵形式：

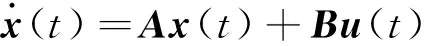
y(t)=Cx(t)

(3)

其中：

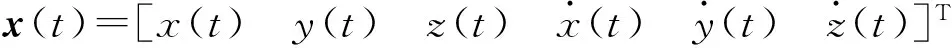
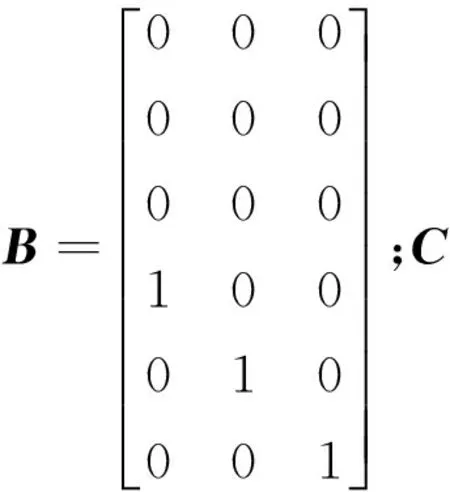
为了利用线性规划方法求解最优脉冲控制，将连续时间系统离散化[18]，设采样周期为T，得到如下形式：

xk+1=F(T)xk+G(T)uk

yk=xk

(4)

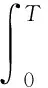
可得：

x2=Fx1+Gu1

=F(Fx0+Gu0)+Gu1

=F2x0+FGu0+Gu1

(5)

依此类推，可得：

xN=FNx0+[FN-1GFN-2G…FG]×

(6)

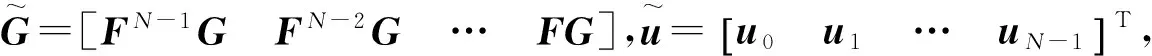
(7)

若以燃料消耗最少为优化目标，则现在的任务就是寻求一组控制过程，使得这一控制过程满足：从初始状态x0到目标状态xN转换的过程中累积消耗的燃料最少。

针对控制任务的离散时间状态空间模型，控制方法的收敛性转变为系统的状态能控性和输出能控性，即，若存在一个分段连续的输入u(t)，能够在有限的时间间隔内，使状态x0到达任意的目标状态xN，那么称状态x(t)在t=t0时是能控的[19]。据式(4)可知，本控制任务的离散时间状态空间模型中状态能控性与输出能控性等价。系统的能控性矩阵为：

[BAB…AN-1B]

此处N=6，能控性矩阵的规模为6×18。易得能控性矩阵关于非零的参考轨道角速率n为行满秩的，其秩为6，那么可知系统是能控的。

下面推导标准的约束形式。

迭代收敛的判别可用形式：|xN-x*|≤ε，其中x*为精确目标状态，ε为误差限，判别式可改写为：

(8)

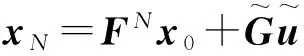
(9)

进一步变形得：

(10)

令：

即可得标准的约束形式：

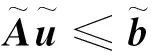
(11)

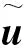
现在，组合式航天器的队形重构问题可以转换为如下线性规划问题(目标函数以及约束函数均为优化变量ui的线性函数)：

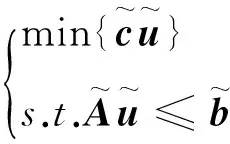
(12)

其中：ui只能在离散的时间点上施加，在计算目标函数值时，ui的分量均取绝对值。

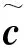
单纯形方法[20]是求解线性规划问题的通用方法。线性规划问题的可行域是n维向量空间Rn中的多面凸集，其最优值如果存在必在该凸集的某顶点处达到。顶点所对应的可行解称为基本可行解。单纯形法的基本思想是：先根据标准的约束形式得到一个基本可行解，从得到的基本可行解出发，按一定规则，寻求另一个能使目标函数值有所改善的基本可行解，依此重复进行，直至得到最优解。因基本可行解的个数有限，故经有限次寻优必能得出问题的最优解。

2.4 组合式航天器构型变换仿真算例

仿真算例问题描述：从跟飞初始状态到面内绕飞椭圆目标状态的队形重构，过程中消耗燃料最优，并要求在规定的时间(可以自行设定)内完成机动。主航天器轨道半径r=7378.137km，L=2.0km，其他尺寸如图4所示。

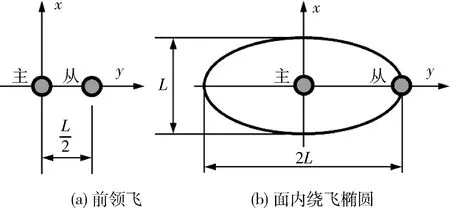
图4 前领飞编队至面内绕飞椭圆的构型变换示意图

2.4.1 构型变换的解析方法实现

据式(2)可知，采用图5所示的面内径向双脉冲机动方法，即可在半个参考轨道周期内完成构型变换机动，从初始的跟飞状态经相对过渡轨迹1，形成绕飞椭圆相对轨迹2。图中Δv1，Δv2分别为第1次、第2次径向速度脉冲增量，且Δv1=nL/16，Δv2=7nL/16[21]。此脉冲实现的解析方法所用总ΔV为0.996m/s。

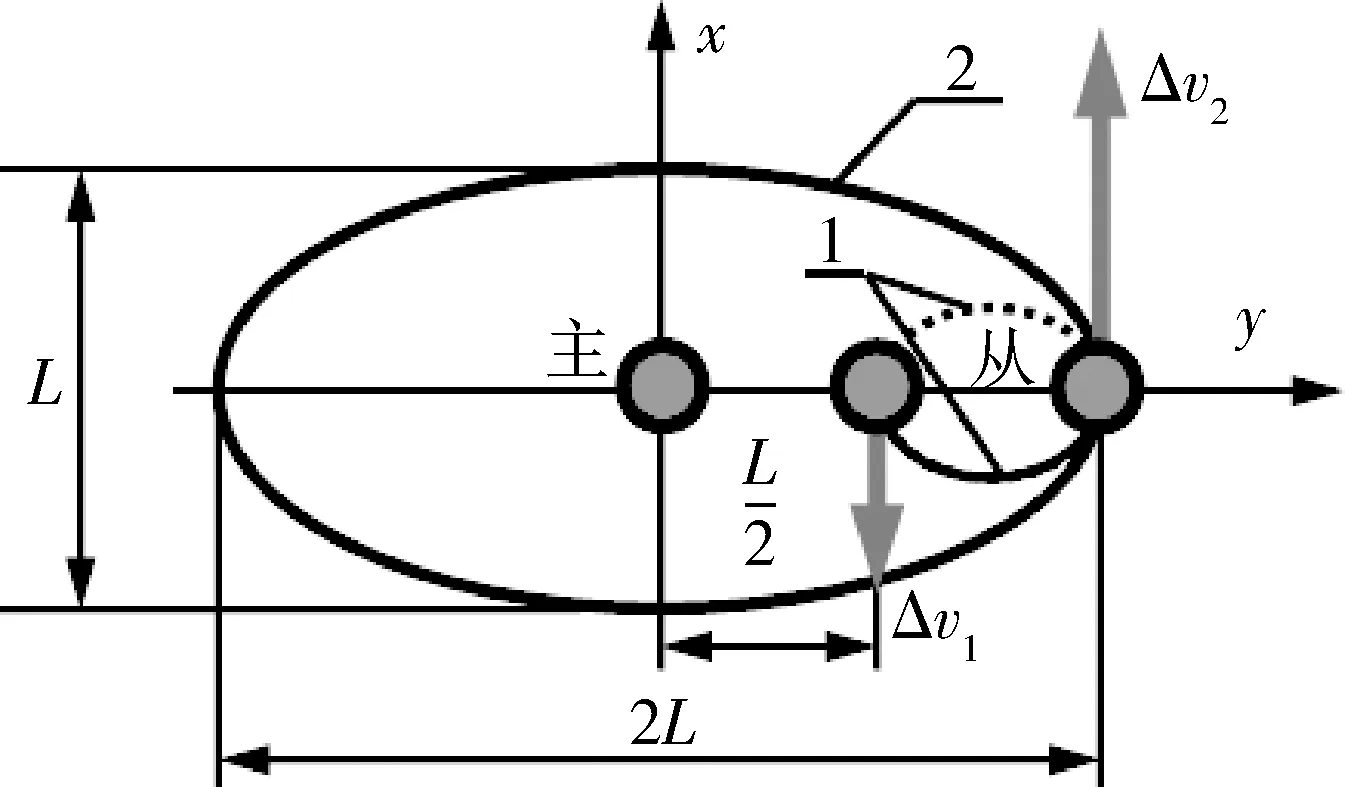
图5 面内径向双脉冲机动示意图(1. 相对过渡轨迹； 2. 相对目标轨迹)

2.4.2 构型变换的优化方法实现

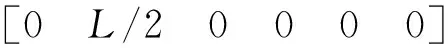
仿真情形4：4个参考轨道周期内，从绕飞椭圆右顶点入轨。仿真输出结果如图6。共4次y方向上的脉冲完成机动；初始与终点时刻都没有脉冲施加，总ΔV为0.498m/s。

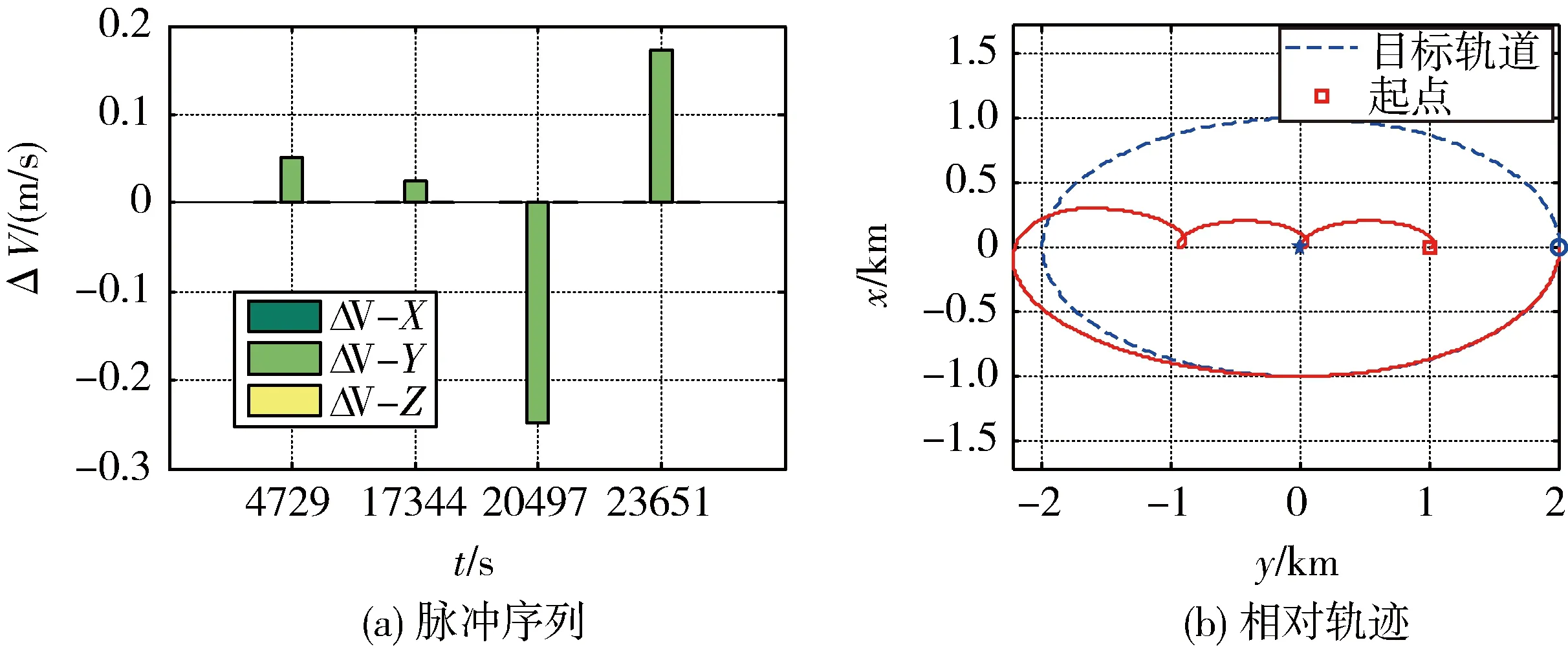
图6 情形4仿真脉冲及相对轨迹

仿真情形8：4个参考轨道周期内，从绕飞椭圆左顶点入轨。仿真输出结果如图7。共4次y方向上的脉冲完成机动；初始与终点时刻都没有脉冲施加。总ΔV为0.498m/s。

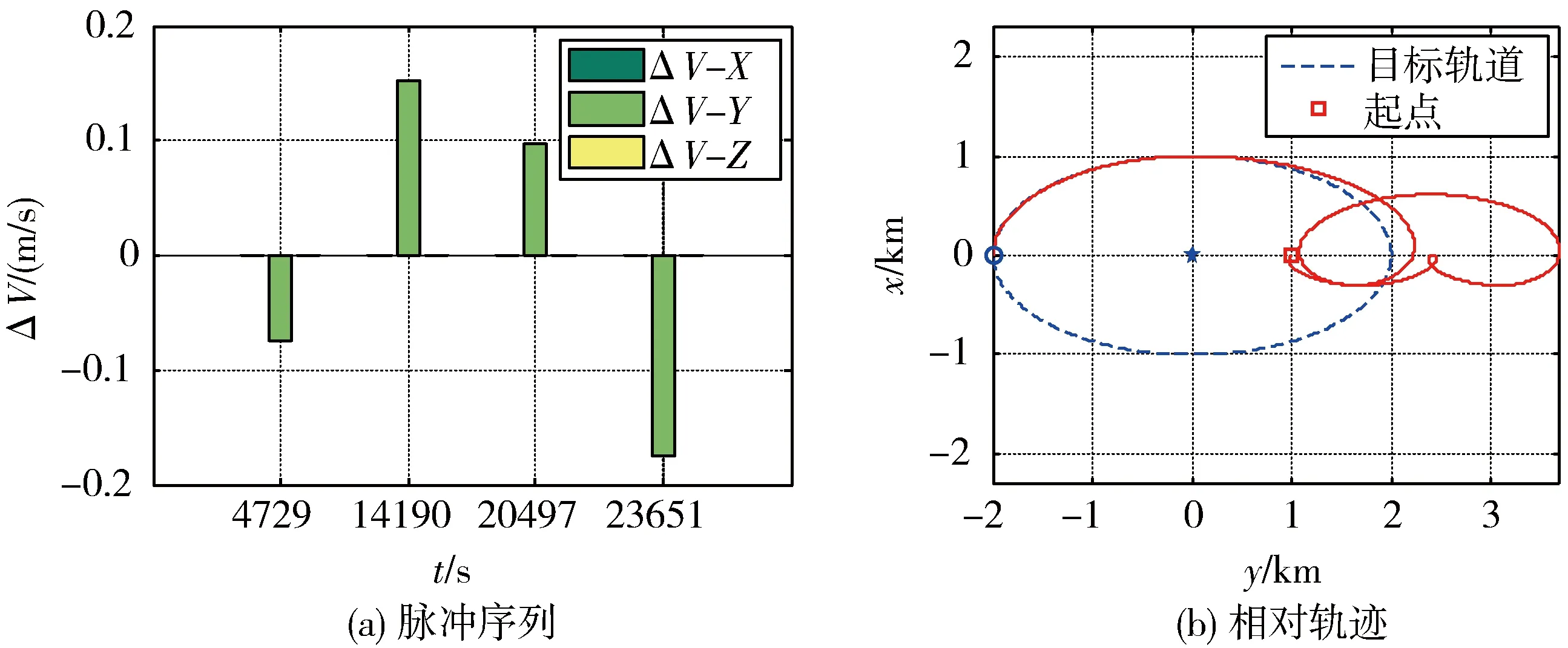
图7 情形8仿真脉冲及相对轨迹

将全部仿真所需速度增量汇总如表1，并将仿真结果与2.4.1小节中的解析结果进行对比，结果表明： 1)机动时长的限制条件越宽松，机动所需总的速度增量越小，越节省燃料； 2)机动时间区间足够大时，进一步改善结果的余地就会越来越小； 3)采用优化方法得到的脉冲序列一般情况下比采用解析方法求得的脉冲序列更省燃料，只有在特定的情况下两者才是一致的(如机动时间限制在半参考轨道周期)，在机动时间足够宽松的情况下，总ΔV节省比例高达50%。

尽管组合式航天器的构型变换过程是在比较近的相对距离内进行的，在机动时间要求比较宽松的情况下，燃料消耗一般比较少，并不一定非要采用燃料消耗最优的控制方式，但在机动时间要求比较苛刻或者任务要求航天器要进行多次分离与组合的情况下，燃料的消耗量有可能非常惊人，这时采用燃料消耗最优的控制方法是有必要的。

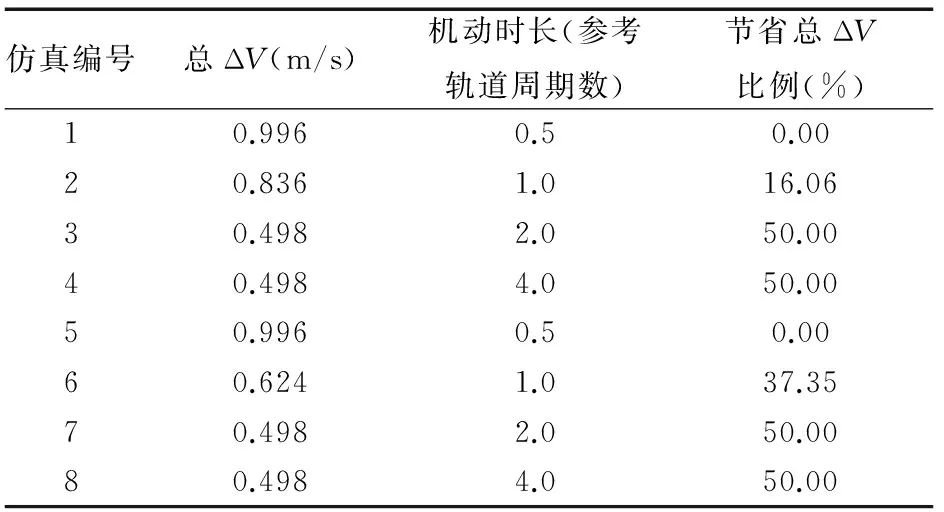
表1 队形重构仿真所需速度增量汇总表

3 结论

组合式航天器是一种可以提高航天任务可靠性的新型航天器。可维护性、规模可缩放性、可重构性等都是新型的组合式航天器系统灵活性和可靠性强的体现。特别是根据空间任务的不同而进行构型变换的能力是组合式航天器完成各种复杂空间任务的必要保证。基于线性规划的最优脉冲控制方法是实现组合式航天器构型变换的一种有效途径。

[1] Falkenhayn E J R.Multimission Modular Spacecraft (MMS)[C].AIAA Space Programs and Technologies Conference.Houston, TX: AIAA, June1988.AIAA-1988-3513.

[2] Larry H C.Modular Spacecraft Structure[P].United States Patent: 6568638 B1, 2003-05-27.

[3] Gerhard B.Satellite Cluster Comprising a Plurality of Modular Satellites[P].United States Patent: 6633745 B1, 2003-10-14.

[4] Brown O, Eremenko P.Fractionated Space Architectures: a Vision for Responsive Space[C].4thResponsive Space Conference.Los Angeles, CA, April 2006.RS4-2006-1002.

[5] Brown O, Eremenko P, Roberts C.Cost-benefit analysis of a Notional Fractionated Satcom Architecture[C].24thAIAA International Communications Satellite Systems Conference (ICSSC).San Diego, California: AIAA, June 2006.AIAA 2006-5328.

[6] Brown O, Eremenko P.The Value Proposition for Fractionated Space Architectures[C].Space 2006.San Jose, California: AIAA, September 2006.AIAA 2006-7506.

[7] Brown O, Long A, Shah N, et al.System Lifecycle Cost under Uncertainty as a Design Metric Encompassing the Value of Architectural Flexibility[C].AIAA SPACE 2007 Conference & Exposition.Long Beach, California: AIAA, September 2007.AIAA 2007-6023.

[8] Deborah M W, Grau J, Jordan L, et al.Modular Spacecraft Standards: Supporting Low-cost, Responsive Space[C].Space 2004 Conference and Exhibit.San Diego, California: AIAA, September 2004.AIAA 2004-6098.

[9] Hironori S，Shinichi N, Chisato K.Propulsion System for Panel Extension Satellite(PETSAT)[C].41stAIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit.Tucson, Arizona, July, 2005.AIAA 2005-3956.

[10] Nicholas R H, Swati M, Simon N, et al.Docking and Reconfiguration of Modular Spacecraft Preliminary SWARM Testing at MSFC[R].Richard T H, Robert D R, eds.Sensors and Systems for Space Applications, Proc.of SPIE 2007.6555, 65550W.

[11] Space Systems Engineering Department of Aeronautics and Astronautics MIT.Self-assembling Wireless Autonomously Reconfigurable Modules[R].Design Document Revision 3.0, 16.83x.December, 2004, 12-15.

[12] Edward A L, David B S, Connie K C.Experimental Demonstration of Technologies for Autonomous on-orbit Robotic Assembly[C].Space 2006.San Jose, California: AIAA, Sep, 2006.AIAA-2006-7428.

[13] 高云峰, 李俊峰.卫星编队飞行中的队形设计研究[J].工程力学, 2003, 20(4): 128-131.(Gao Yunfeng, Li Junfeng.The Relative Trajectory Design of Satellite Formation Flying[J].Engineering Mechanics, 2003, 20(4): 128-131(in Chinese).)

[14] 朱仁璋.航天器交会对接技术[M].北京: 国防工业出版社, 2007: 205-244.(Zhu Renzhang.Rendezvous and Docking Techniques of Spacecraft[M].Beijing: National Defence Industry Press, 2007: 205-244(in Chinese.)

[15] 朱仁璋, 汤溢.空间交会接近与绕飞设计[J].中国空间科学技术, 2005, 1: 7-14.(Zhu Renzhang, Tang Yi.Design Methods for the Closing and Fly-around of Space Rendezvous[J].Chinese Space Science and Technology, 2005, 1: 7-14(in Chinese).)

[16] 湛颖, 黄文虎, 倪茂林,等.多冲量最优交会的动态规划方法[J].宇航学报，1993, 2: 1-7.(Chen Ying, Huang Wenhu, Ni Maolin, et al.Dynamic Programming Method for Optimal Multi-impulse Rendezvous[J].Journal of Astronautics, 1993, 2: 1-7.)

[17] Vallado D A.Fundamentals of Astrodynamics and Applications[M].3nd ed.New York:Springer,2007:389-412.

[18] 俞立.现代控制理论[M].北京: 清华大学出版社, 2007: 38-63.(Yu Li.Modern Control Theory[M].Beijing: Tsinghua University Press, 2007: 38-63(in Chinese).)

[19] Benjamin C K，Farid G.Automatic Control Systems[M].8nd ed.Beijing:Higher Education Press,2003:169-177.

[20] 陈宝林.最优化理论与算法[M].2版.北京: 清华大学出版社, 2005: 37-93.(Chen Baolin.Optimization Theory and Algorithm[M].2nd ed.Beijing: Tsinghua University Press, 2005: 37-93(in Chinese).)

[21] 张育林, 曾国强, 王兆奎,等.分布式卫星系统理论及应用[M].北京: 科学出版社, 2008: 88-100.(Zhang Yulin, Zeng Guoqiang, Wang Zhaokui, et al.Theory and Application of Distributed Satellites System[M].Beijing: Science Press, 2008:88-100(in Chinese).)