基于灰色模型的导弹水中段横向载荷计算

王浩宇 王 军 张 涛

1.海军装备部, 北京 100841 2.中国人民解放军91868部队, 三亚 572016 3.海军装备研究院, 北京 100073

潜射导弹由于其天然的隐蔽性优势，是目前导弹发射的主要方式之一。导弹水中段(本文定义导弹从离开发射管到完全脱离水面的行程为水中段)由于受到海水液态介质的影响，其横向载荷相对于在大气层中的空气介质的影响更大。另外，由于受到发射深度、发射平台的运动状态、洋流、洋面风力、波浪等因素的存在，使得导弹在水中段受到随机干扰，其横向载荷难以进行精确的数学解析建模，无法获得准确数据。横向载荷过大将直接导致导弹折断的严重后果。这对弹体结构强度的设计提出了严峻的挑战，而设计需要数据的支持。

针对水中段横向载荷对弹体结构设计的要求，目前国际上一般采取模拟水下发射环境，在导弹上安装传感器，通过试验获得导弹水中段的横向受力情况。此种方式存在如下缺点：一方面，模拟的水下发射环境难以对所有发射海况进行模拟；另一方面，受到经费、时间、试验条件等的制约，其试验次数也是有限的。因此，获得的试验数据必然是有限的，不全面的。通过这些有限的数据进行导弹结构强度的设计显然存在一定的风险。还有一种方式就是针对水中段弹体的受力进行力学建模，通过受力分析来设计弹体结构强度。这种方式的突出问题是水中段的随机干扰造成横向载荷难以进行精确的数学解析建模，因而无法获得设计所需的精确数据。

灰色系统理论的研究对象是“部分信息已知，部分信息未知”的“小样本”、“贫信息”不确定性系统，通过对部分已知信息的探索，实现对事物的确切认识[1]。显然，导弹水中段横向载荷的计算具有灰色系统的显著特点，适合采用灰色系统理论思想进行建模和计算。

1 灰色系统相关理论

采用灰色系统理论进行建模分析一般经历思想开发、因素分析、量化、动态化及优化5个步骤[2]。这其中，第4步动态化最为关键。主要是利用各环节的输入和输出数据建立数据序列，建立动态GM(Grey Model)模型，即动态模型。下面就本算法所涉及的灰色系统理论的相关概念和理论进行阐述。

1.1 序列算子

设X为系统行为数据系列

X=(x(1),x(2),…,x(n))

(1)

D为作用于X的算子，X经过算子D作用后所得序列记为

XD=(x(1)d,x(2)d,…,x(n)d)

(2)

称D为序列算子，XD为一阶算子作用序列。序列算子可以多次作用，相应的称为二阶、三阶等序列算子。若

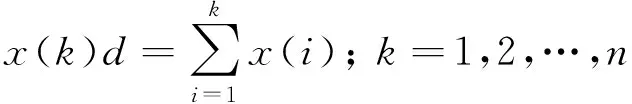
(3)

则称D为X的一次累加算子。相应的m阶算子Dm称为X的m次累加算子，记为“r-AGO”(Accumulating Generation Operator)。

若如下关系式成立

Z(k)=0.5x(k)+0.5x(k+1),k=1，2,…,n

(4)

则Z是X的紧邻均值生成序列。

1.2 序列光滑性检验

序列X的光滑比ρ(k)定义如下

(5)

若序列X满足

(6)

则称X为准光滑序列。

1.3 序列的准指数规律检验

如公式(1)所示序列X，称

(7)

为序列X的级比。若σ<0.5，则称X具有准指数规律。

1.4 GM(1，1)模型

令：

(8)

称

x(0)(k)+ax(1)(k)=b

(9)

为GM(1，1)模型的原始形式，第1个“1”表示“一阶方程”，第二个“1”表示“1个变量”。

x(0)(k)+az(1)(k)=b

(10)

为GM(1，1)模型的基本形式。令

(11)

(12)

参数-a表示发展系数，b为灰色作用量。

方程

(13)

为公式GM(1，1)模型公式(10)的白化方程。

运用GM(1，1)模型时，需要考虑以下条件的限制[3]：

1)|a|≥2时，GM(1，1)模型无意义；

2 仿真建模及检验

仿真建模的目的是在有限试验数据的基础上，建立导弹水中段横向载荷的预测模型，以此对不同发射环境下的横向载荷进行预测，从而为弹体结构强度设计及弹道计算提供支撑。

2.1 仿真建模及检验思路

试验时一般获得不同发射条件下的数据，首先根据发射条件的恶劣程度，比如海浪的大小，进行数据分类，按照升序或者降序排列；然后针对试验数据建立恰当的灰色模型；模型有效性检验；最后针对检验结果决定是否对模型参数进行修正，直到得到满意的模型为止。具体思路如图1所示。

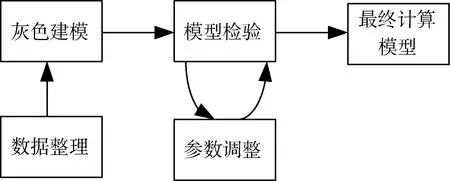
图1 仿真建模及检验思路

2.2 仿真建模

依据上述建模思路，针对某型导弹水中段的最大横向载荷试验数据进行整理后排序如下：2.874，3.278，3.337，3.390，3.679，3.7576，选取前5个(最后1个用于数据预测检验)整理成如下序列

X0=(x0(1),x0(2),…,x0(5))

=(2.874,3.278,3.337,3.390,3.679)

(14)

Step1：对X0进行一次累加算子1-AGO

X1=(x1(1),x1(2),…,x1(5))

=(2.874,6.152,9.489,12.879,16.558)

(15)

Step2：对X0进行光滑性检验

由公式(6)得

(16)

满足光滑性条件。

Step3：对X1准指数规律检验：

由公式(7)得，

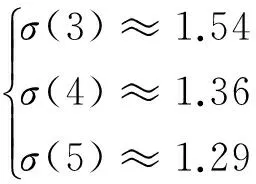
(17)

满足准指数规律，可对X1进行GM(1,1)建模。

Step4：生成X1的紧邻均值生成序列：

由公式(4)得，

Z(1)=(4.513,7.820,11.184,14.718)

(18)

由公式(11)得，

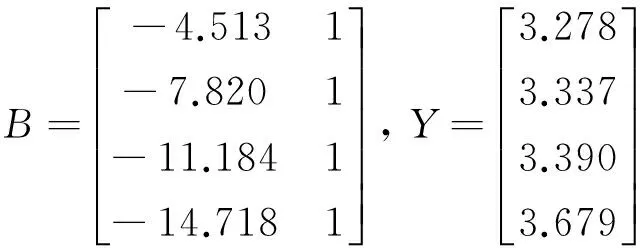
(19)

Step5：确定参数及模型

由公式(12)得，

(20)

因此，由公式(13)得GM(1，1)模型的白化方程为：

(21)

由x(1)(0)=x(0)(0)，则此微分方程解(时间响应式[4])可写为：

=85.276151e0.0372k-1-82.402151

(22)

2.3 模型检验

检验思路如下：针对公式(21)及(22)建立的GM(1，1)模型，计算出原始序列的还原值，然后比较此还原值和原始序列，进而检验模型的可信度。

由公式(22)得，

=(2.8704,6.1060,9.4605,12.9422,16.5558)

(23)

由一次累加算子1-AGO的定义有，

(24)

因此，

=(2.8740,3.2320,3.3545,3.4817,3.6136)

(25)

综合上述数据，整理可得如下计算结果，如表1所示，误差计算公式如下：

(26)

表1 模型检验结果

可见，GM(1，1)模型的计算公式(22)在所利用的数据范围内(原始数据的前5个，即公式(14)所示序列)具有较好的模拟精度。下面针对模型的数据预测精度进行检验。以原始数据的最后1个：3.7576，进行检验。

由公式(22)及(24)得，

(27)

残差为3.7576-3.7482=0.094；相对误差为：0.094÷3.7576=2.50%。显然，所建立的模型对于未经采用数据的模拟同样具有较高的精度。

3 结束语

由于受到发射深度、发射平台的运动状态、洋流、洋面风力、波浪等因素的影响，使得导弹在水中段受到随机干扰，其横向载荷难以进行精确的数学解析建模，从而无法获得精确数据。而试验又受费用、环境等因素制约，不可能获取全部发射条件下的数据。本文针对“小样本”、“贫信息”的特点，采用灰色系统理论思想对导弹水中段的横向载荷进行建模和计算。通过分析已知数据的特点，建立了GM(1,1)结构形式的计算模型。数据检验表明:所建立的计算模型不但能够有效的模拟建模使用过的原始数据，而且对于未使用过的数据的模拟同样具有很好的精度。

[1] 邓聚龙.灰色系统理论教程[M].武汉：华中理工大学出版社，1990.

[2] 刘思峰，党耀国邓.灰色系统理论及其应用[M].北京：科学出版社，2004.

[3] Lin Changrong & Deng Julong.On Grey Prediction of Gas Pool[M].武汉：华中理工大学出版社，1996.

[4] 王学萌，张继忠，王荣.灰色系统分析及实用计算程序[M].武汉：华中科技大学出版社，2001.