基于线性矩阵不等式的动态控制分配方法研究

臧希恒 唐 硕,2

1. 西北工业大学航天学院，西安 710072 2. 航天飞行动力学技术重点实验室，西安 710072

控制分配在飞行控制系统[1-3]、舰船控制系统[4-5]及其他冗余控制系统中扮演着重要的角色。控制分配模块给执行机构(如飞行器的副翼、升降舵、襟翼、方向舵和推力矢量，及舰船推进器、舵、螺旋桨等)发送控制指令来产生由上级控制系统所输出的需用控制输入指令(如力、力矩、加速度等)。如何将这些虚拟的或者说是广义的控制指令转换为实际的执行机构控制指令称为控制分配问题。图1阐明了上述控制问题的基本结构。

图1 控制分配问题结构图

基于Durham[1-3]在控制分配领域的研究工作，一些控制分配方法在上个世纪末得到了广泛的研究[6-11]，现有的控制分配技术大多为线性控制分配，即假设虚拟控制输入与执行机构的效率为线性函数，现有线性控制分配方法总体可分为2大类:非优化控制分配方法和基于数值优化的控制分配方法。非优化控制分配方法主要有直接法、伪逆法、串式链法等，而基于数值优化的控制分配方法的典型代表是有约束线性规划，混合整数规划，二次规划等。现有的控制分配技术的综述性研究见文献[12-14]，Page 和Steinberg[13-14]对于大多数常见的线性控制分配算法进行了大量的开闭环仿真实验，并总结各种控制分配算法的优缺点。另一方面，Bodson[12]比较了基于数值优化方法的有约束控制分配方法，并给出了其在实时飞行控制系统中可行性的建议。

一般而言，控制分配的目标是通过产生合理的执行机构指令来获得所需的机体控制输入，同时又必须满足各种严格的约束。迄今为止,大多数的控制分配算法都倾向于忽略执行机构动态性的影响，或者分开处理执行机构动态性[6-14]。为了便于问题的处理，通常假设执行机构没有动态性，或者是相对于飞行器来说足够快以至于可以忽略其动态性。然而执行机构动态性的出现将降低整个控制系统的有效带宽，甚至可以加重未建模非线性的负面影响。Oppenheimer 和Doman[15-16]已经表明了执行机构动态性对控制分配有着重要的影响并且提出了一种补偿执行机构动态性的方法。然而，这种方法只能适用于一阶和二阶执行机构。Härkegåxd[17]通过增加对执行机构速率的惩罚扩展了一般的二次规划控制分配算法，使算法具有频率依赖的特性，实现了对执行机构带宽的考虑，这种控制分配方法被他命名为“动态”控制分配，然而这种方法严格意义上并没有将全部的执行机构动态性信息考虑到算法中来，只能算得上是一种伪动态控制分配算法，但是其研究成果却促进了广大学者对动态控制分配算法的研究。文献[18-20]提出的模型预测动态控制分配方法利用执行机构模型来预测所需的执行机构状态和控制输入轨迹，并且以最优轨迹的跟踪问题来决定控制分配的解。但是这种方法需要一个预测模块来预测控制输入指令、执行机构状态和输出轨迹，因此需要对控制指令提前预测。通常想要得到控制输入的预测是不现实的，这就限制了轨迹跟踪问题的求解。

本文将针对线性控制分配技术展开研究，提出一种系统地处理动态控制分配问题的新方法，采用基于数值优化的方法来解决控制分配问题，将基于有约束二次规划的静态控制分配加入全部的执行机构动态性信息，并将问题转化为基于线性矩阵不等式(Linear Matrix Inequality, LMI)的目标函数最小化问题，最后给定一组变频率三通道控制输入指令，对文中的动态控制分配方法进行仿真验证，并将其与经典的基于线性规划(LP)的静态控制分配方法进行比较，仿真结果表明本文提出的动态控制分配算法显著提高了控制输入跟踪的鲁棒性、精确性与有效性。

1 控制分配问题描述

控制分配在冗余系统中扮演着重要的角色，特别是在执行机构存在饱和限制、效率差异性以及动态性时，其作用更是举足轻重。同时，当控制分配与控制器分开设计时，可以实现执行机构故障下的重构控制，而不用重新设计系统的控制器。图2为一般采用控制分配的控制系统结构图，同时也是静态控制分配的结构图。r(t)为参考输入指令即为飞行控制系统中的制导指令，所需控制力矩udes由控制器给出，用来跟踪r(t)，而udes由执行机构指令偏转δcmd产生，uact为由执行机构实际偏转δact产生的实际控制力矩，直接作用于机体。本文假设控制力矩与执行机构偏转之间呈线性关系，即所谓线性控制分配问题，其形式如式(1)所述

udes=Beffδcmd

(1)

给定所需的控制力矩udes，控制效率矩阵Beff求解执行机构指令偏转δcmd即为控制分配问题，同时执行机构还需满足下列位置和速率约束：

执行机构位置约束

δmin≤δact≤δmax

(2)

执行机构速率约束

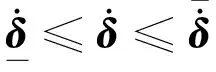
(3)

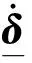
现代飞行器一般采用数字控制系统，飞行控制律为采样周期T的离散时间系统，可以将上述位置和速率约束合并为下面的组合时变位置约束

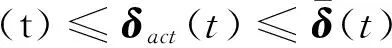
(4)

其中

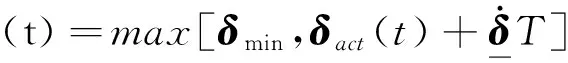
(5)

方程(1),(4)和(5)即构成了控制分配问题的数学模型，从上述方程可见模型中并没有包含执行机构的动态性信息，即忽略了执行机构的动态性，因此上述控制分配问题即为经典的静态控制分配问题。当执行机构带宽无限大即执行机构动态性为1时，δact=δcmd，相应的uact=udes，系统可以完成对参考输入的准确跟踪；相反地，当执行机构存在有限带宽时，执行机构偏转指令必然受到执行机构动态性的削弱，即δact≠δcmd，这就导致uact≠udes。只有uact=udes时系统才能完成对参考输入的准确跟踪，因此忽略执行机构动态性会降低系统对参考输入跟踪的准确性，甚至无法完成对参考输入指令的跟踪。

2 基于LMI的动态控制分配

2.1 执行机构动态性

假设执行机构系统有m个具有线性动态的执行机构，第j个执行机构的阶数为nj，j=1,2,…,m。

假设1：执行机构系统动态性是已知、时不变并且完全解耦的，即每两个执行机构之间是独立互不影响的，则整个执行机构动态系统的状态空间表示为

δact=Cactxact

(6)

其中，状态为xact∈RN，输入为δcmd∈Rm，输出为δact∈Rm，状态矩阵为Aact∈RN×N，输入矩阵为Bact∈RN×m，输出矩阵为Cact∈Rm×N，并且

(7)

通过假设1可知，其中Aact，Bact，Cact均具有块对角结构，即

Aact=diag([Aact,1,Aact,2,…,Aact,m])

Bact=diag([Bact,1,Bact,2,…,Bact,m])

Cact=diag([Cact,1,Cact,2,…,Cact,m])

将方程(6)进行离散化，可得等价的离散执行机构动态系统为

xact(k+1)=Axact(k)+Bδcmd(k)

δact(k)=Cxact(k)

(8)

其中A，B和C为具有合适维数的采样时间T对应的离散域执行机构动态系统的参数矩阵。

假设2：(A,B)是可控的并且对于任意k≥0，(A,C)是可观测的。

假设3：对于执行机构离散时间模型，矩阵CB是非奇异的，因此对于输入δcmd(k)的响应反映在输出δact(k+1)上。

2.2 动态控制分配问题描述

顾名思义，动态控制分配即为考虑执行机构动态性的控制分配算法，即当执行机构存在有限带宽时，仍存在uact=udes，可以实现参考输入指令的准确跟踪，现将第一节中描述的静态控制分配问题进行扩展，可得下列动态控制分配的数学模型

udes=Beff(k+1)δact(k+1)

(9)

xact(k+1)=Axact(k)+Bδcmd(k)

δact(k)=Cxact(k)

(10)

其中

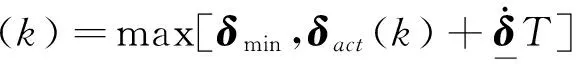
(11)

方程(9)和(10)的物理意义即为在满足执行机构偏转约束和动态性的前提下，求解执行机构指令偏转δcmd(k)，值得一提的是虽然方程(9)中执行机构偏转为实际偏转，但是动态控制分配问题仍然是为了求解指令舵偏δcmd(k)，上述动态控制分配原理见图2,由图中可见动态控制分配模块中已经包含了全部的执行机构动态性信息，因此不需要对指令舵偏δcmd(k)进行二次处理便可以完成力矩指令的精确跟踪。相应的静态控制分配结构图见图3。

图2 动态控制分配结构图

图3 静态控制分配结构图

2.3 LMI初步

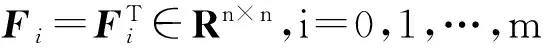
F(x)=F0+x1F1+…+xmFm0

(12)

定理1 对于给定的对称矩阵

(13)

其中F11(x)是方阵。以下3个条件是等价的：

1)F(x)0；

2)F11(x)0,且

F22(x)-F21(x)[F11(x)]-1F12(x)0；

3)F22(x)0,且

F11(x)-F12(x)[F22(x)]-1F21(x)0。

其中2)和3)表示的不等式即为x的非线性约束。利用这个定理可以将形如2)和3)的非线性矩阵不等式转化为线性矩阵不等式，这个定理非常重要，下一节通过定理1将执行机构的动态控制分配问题转化为基于线性矩阵不等式的目标函数最小化问题。

2.4 动态控制分配的LMI描述

基于有限带宽执行机构的动态控制分配问题可以转化为具有下述二次性能指标的优化问题，亦即二次规划问题，

Beff(k+1)δact(k+1)]

(14)

其中Wδ=diag([wδ,1,wδ,2,wδ,3,…,wδ,m])为正定对称矩阵，wδ,i指定了第i个执行机构相对权重。Wu=diag([wu,1,wu,2,wu,3,…,wu,p])为正定对称矩阵，wu,j指定了第j个方向力矩误差的相对权重，对于飞行器姿态控制，p=3分别代表滚动、俯仰、偏航三个通道力矩误差。方程(14)中第1项代表了最小净执行机构偏转控制，而第2项则代表了最小力矩误差控制，显而易见应该首先保证力矩指令的准确跟踪，因此权重矩阵Wu应该远远比矩阵Wδ要大，第1项相当于是第2性能指标，目的是为了确保在第2项的解不唯一时规划问题仍然可以收敛到唯一解。

这里引入一个松弛变量γ>0，令目标函数的最小值小于γ，

γ-J>0

(15)

即

Beffδact(k+1)]>0

(16)

显而易见方程(16)为一个凸非线性矩阵不等式，依据定理1可以将其转化为一个线性矩阵不等式，见方程(17)。

(17)

为了便于线性矩阵不等式优化问题的求解，实际的执行机构偏转约束可以改写为式(18)形式，

eiδact(k+1)-eiδ(k+1)>0,i=1,2,…,m

(18)

其中ei和ej为沿着δact,i和δact,j的单位矢量。联立方程(8)、(17)和(18)的动态控制分配问题转化为方程(19)所示的具有线性矩阵不等式约束的目标函数最小化问题。

γ>0

eiδact(k+1)-eiδ(k+1)>0,i=1,2,…,m

其中

xact(k+1)=Axact(k)+Bδcmd(k)

δact(k)=Cxact(k)

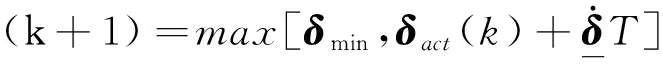
(19)

方程(19)所述LMI优化问题利用标准的算法很容易求解。根据当前的控制输入力矩即可求解执行机构偏转指令。对于飞行控制系统来说，在线实时求解方程(19)有些困难，优化问题的求解是迭代的。然而方程(19)构成了一个凸优化问题，可行解存在时收敛性可以得到保证。随着计算技术的发展，方程(19)作为飞行控制系统在线控制分配可能成为现实。下一节中将结合具体实例进行仿真，并通过本算法分别与带执行机构动态性补偿和不带执行机构动态性补偿的基于线性规划的静态控制分配方法进行比较，验证基于LMI动态控制分配算法的有效性。基于线性规划的静态控制分配方法详见文献[12]。

3 仿真结果与分析

本节将针对飞行器的气动舵面控制分配问题展开研究，并分别采用静态控制分配方法和本文提出的动态控制分配方法进行仿真验证。假设飞行器具有4个气动舵面，选取4个气动舵面主要是为了让气动舵面控制存在冗余，舵面1和舵面2为具有零点的二阶线性模型，舵面3为经典的二阶振荡环节，舵面4为一阶惯性模型。气动舵面的动态性如下：

(20)

气动舵面效率矩阵对于所有的k均为时不变的。

(21)

气动效率的单位为rad/s2/(°)。每一个气动舵面都具有位置和速率饱和约束：

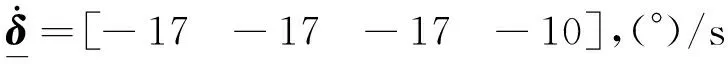
(22)

选择这样的约束是为了使至少一个舵面的位置或速率在仿真的过程中达到饱和。这样做的目的是为了验证当执行机构出现饱和时本文提出的动态控制分配算法依然有效。控制指令信号包含了滚转、俯仰、偏航三通道的幅值为0.15,0.3,0.15的连续变频信号，在10s的时间间隔里频率范围为0.5Hz到2Hz。

(23)

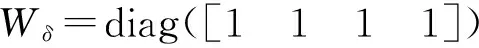
分别采用基于LP的静态控制分配方法和基于LMI的动态控制分配方法进行仿真，图4和5为基于LP的静态控制分配方法在考虑舵面动态性时的仿真结果，其中图4为控制指令的跟踪响应曲线，得到了几乎理想的跟踪精度，图5为其舵面实际偏转指令，可见随着所需控制输入指令频率的增大，舵面3和舵面4逐渐趋于速率饱和。图6和图7为基于LP的静态控制分配方法考虑舵面动态性时的仿真结果，从图6的控制输入跟踪结果可见控制分配方法完全失去其有效性，随着控制输入指令频率的增大，实际舵偏产生的实际控制输入无法快速响应并跟踪所需控制输入指令。图7给出了舵面指令舵偏与实际舵偏的差异，这是由于舵面存在动态性，对指令舵偏信号造成了削弱，从而直接导致了实际舵偏无法跟踪振荡多变所需控制输入udes。图8～10给出了基于LMI的动态控制分配方法在考虑舵面动态性的仿真结果，图8显示该方法得到了与图4媲美的跟踪精度，图9给出了指令舵偏与实际舵偏的对比曲线，从图中可以看出指令舵偏都较实际舵偏大得多，这主要是由于控制分配方法内部包含了全部舵面的动态性信息，使其可以“预知”舵面动态性对指令舵偏的削弱效果，因此基于LMI的动态控制分配方法给出的指令舵偏在经过舵面动态性环节后产生的实际舵面偏转指令仍然可以实现对所需控制输入指令的精确跟踪。图10给出了实际舵偏的放大图，对比图10与图5可以看到基于LMI的动态控制分配方法在考虑舵面动态性时的实际舵偏指令与基于LP的静态控制分配方法不考虑舵面动态性的实际舵偏有惊人的相似之处，这就进一步验证了本文所提出的动态控制分配方法的有效性。总而言之，图4～10显示了传统的静态控制分配方法在忽略执行机构动态性时可能会造成跟踪性能的下将并降低系统的鲁棒性，同时也验证了基于LMI的动态控制分配方法提高了系统的鲁棒性、精度和有效性。

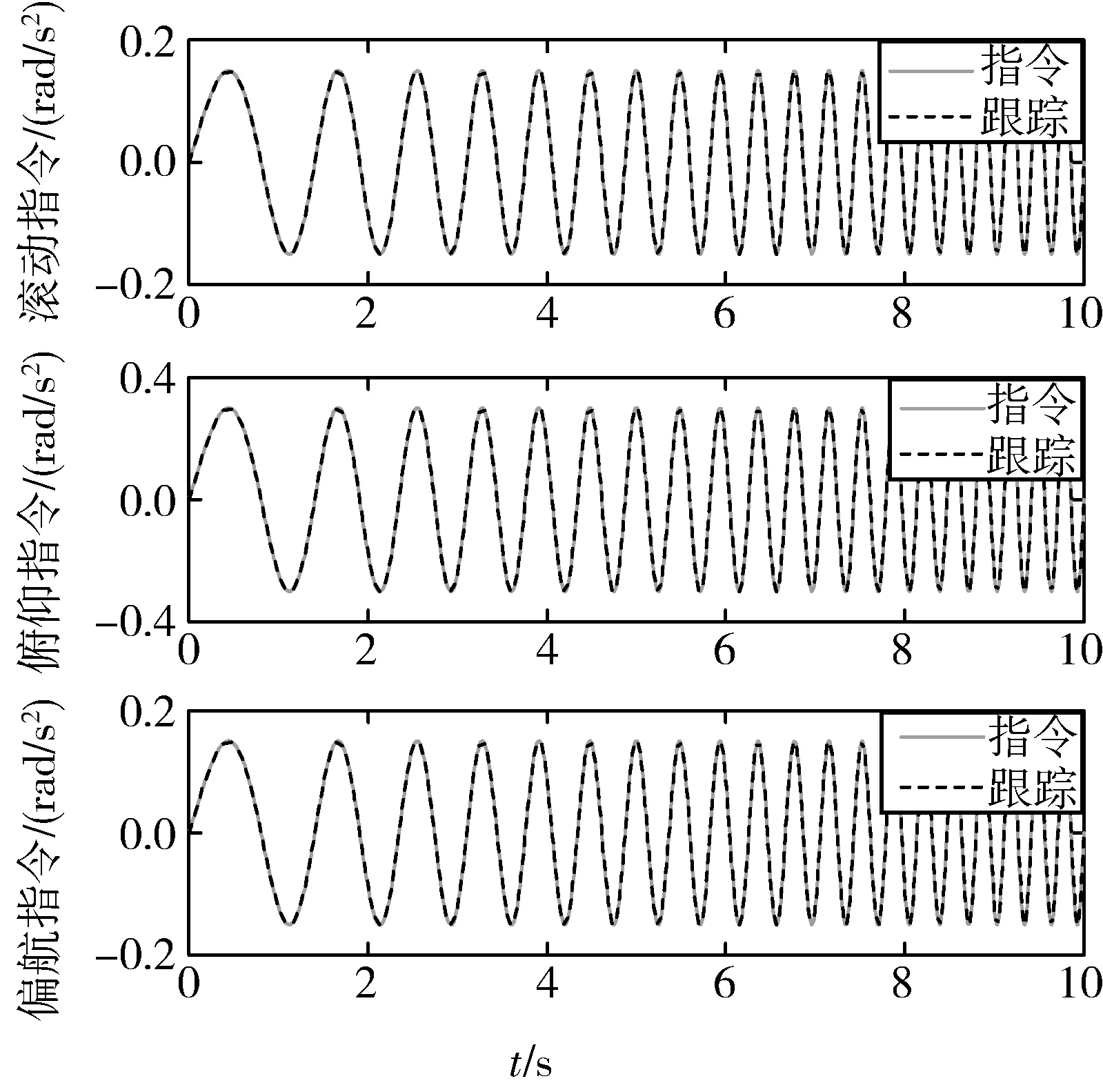
图4 控制指令跟踪：静态LP(不考虑舵面动态性)

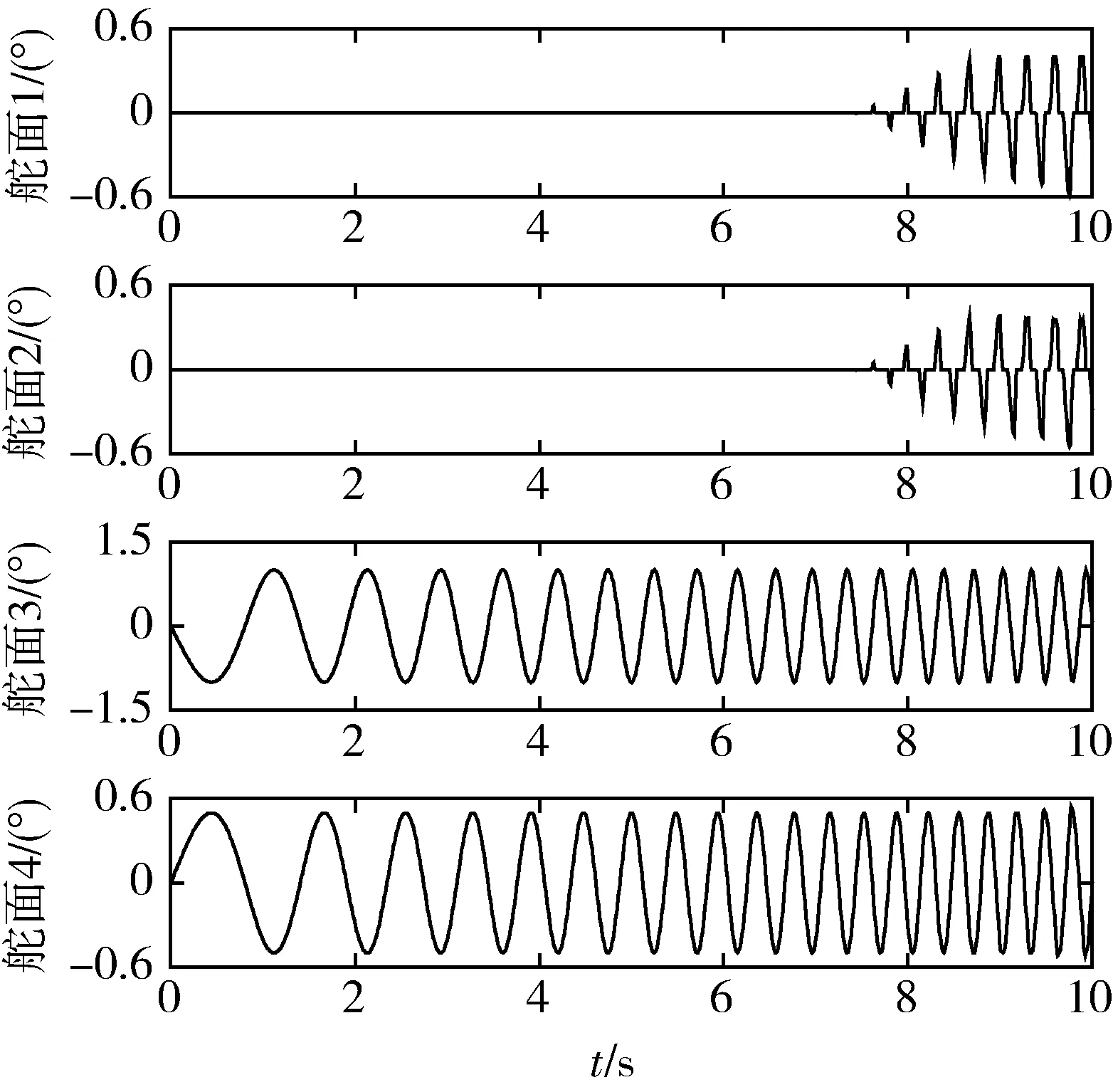
图5 实际舵面位置：静态LP(不考虑舵面动态性)

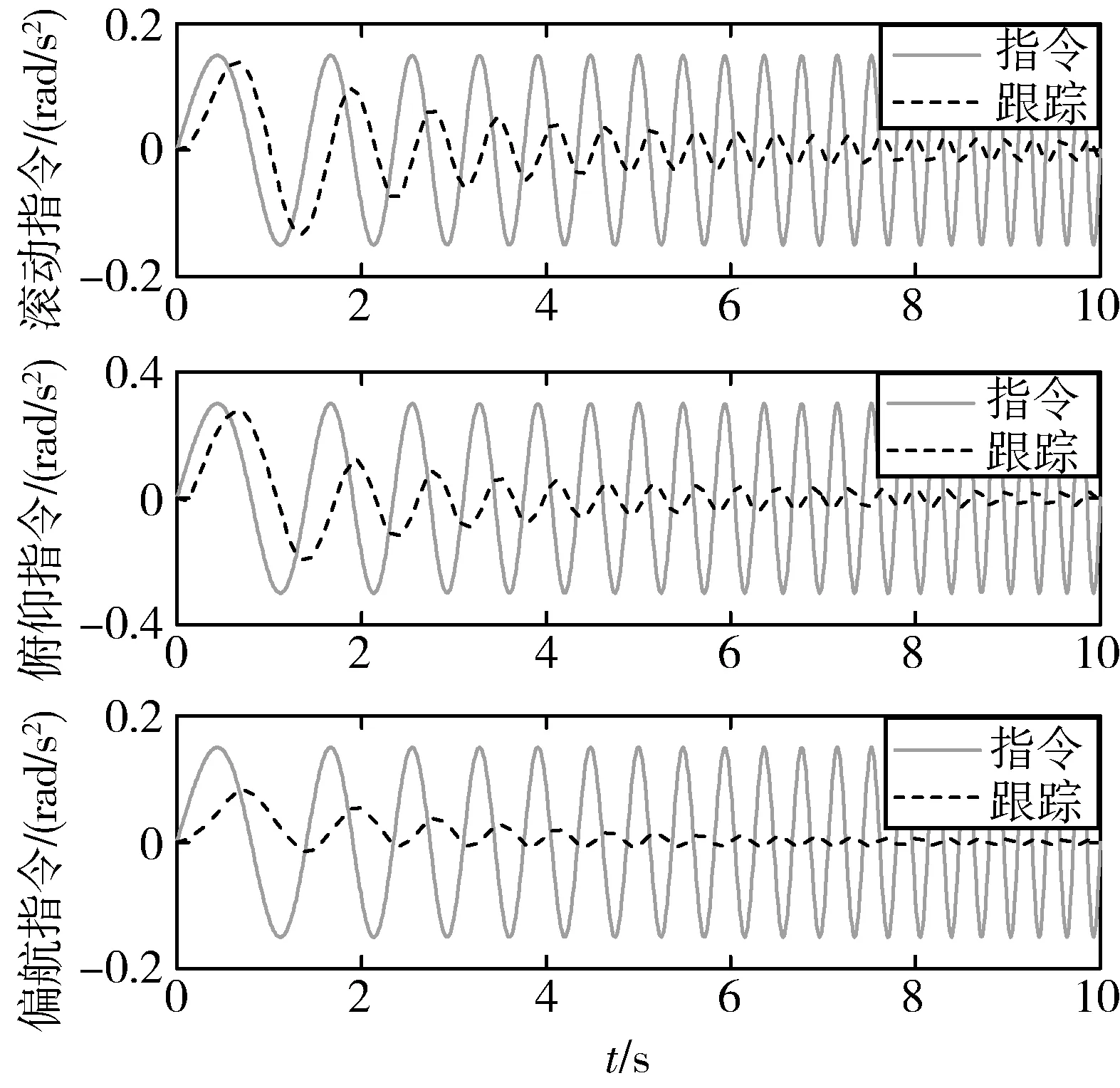
图6 控制指令跟踪：静态LP(考虑舵面动态性)

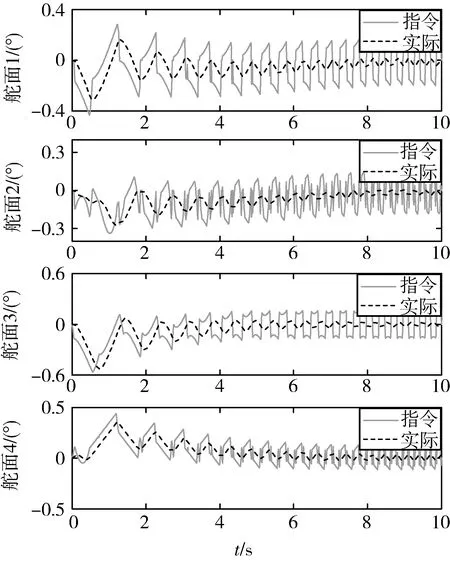
图7 指令舵面位置和实际舵面位置：静态LP(考虑舵面动态性)

图8 控制指令跟踪：动态LMI(考虑舵面动态性)

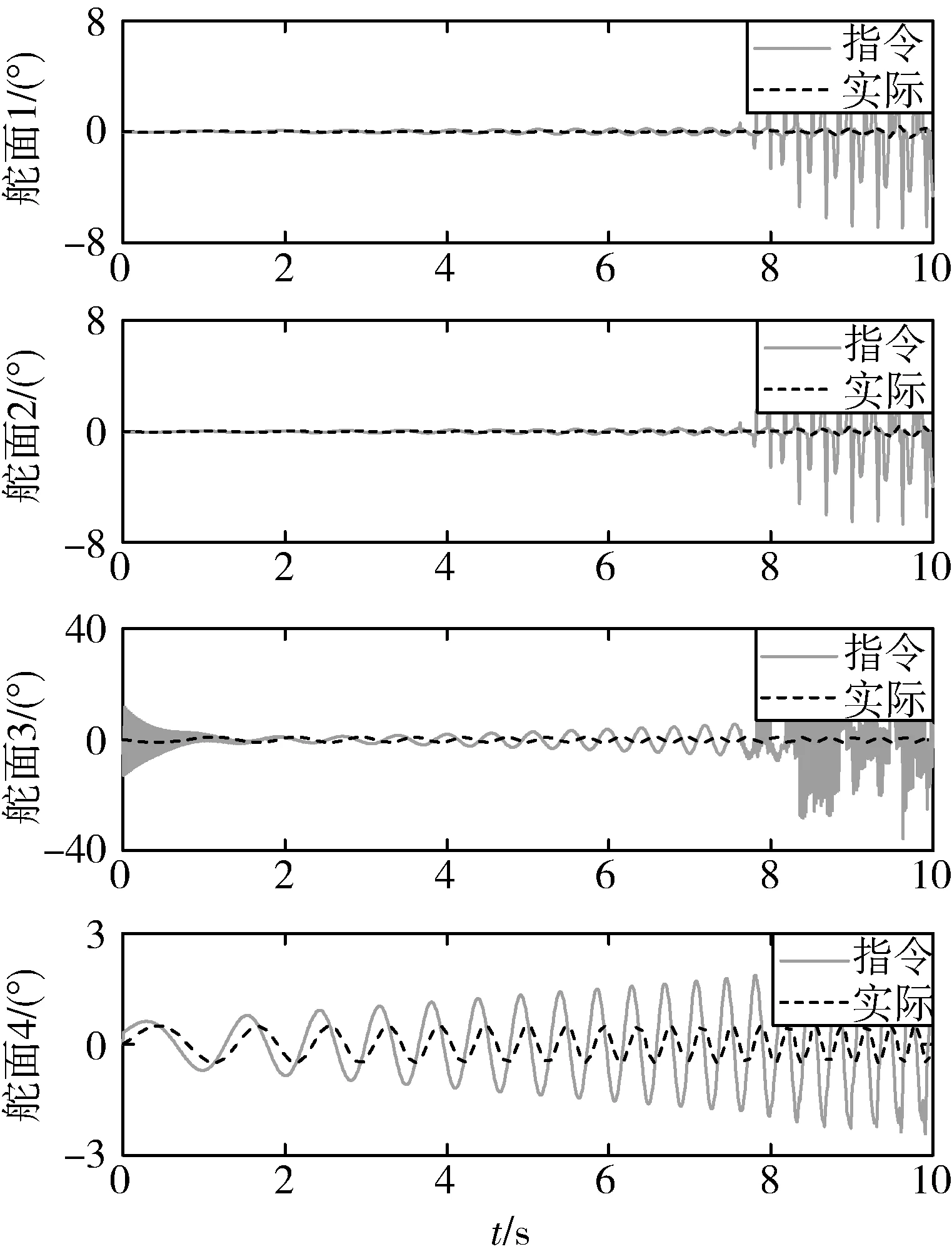
图9 指令舵面位置和实际舵面位置：动态LMI(考虑舵面动态性)

图10 实际舵面指令：动态LMI(考虑舵面动态性)

4 结论

在设计控制分配方法时不考虑执行机构动态性可能会导致系统性能的急剧下降，减小系统的有效带宽。文中提出了一种新的基于LMI的动态控制分配方法，消除了执行机构动态性对控制分配模块潜在的不良影响，并显著提高了控制系统的精度。

[1] Durham W C.Constrained Control Allocation[J].Journal of Guidance，Control，and Dynamics，1993，16(4)： 717-725.

[2] Durham W C.Constrained Control Allocation: Three Moment Problem[J].Journal of Guidance，Control，and Dynamics，1994，17(2)： 330-336.

[3] Durham W C，Bordignon K A.Multiple Control Effector rate Limiting[J].Journal of Guidance，Control，and Dynamics，1996，19(1)： 30-37.

[4] Sørdalen O J.Optimal Thrust Allocation for MarineVessels[J].Control Engineering Practice，1997，5： 1223-1231.

[5] Berge S P，Fossen T I.Robust Control Allocation of Overactuated Ships: Experiments with a Model Ship[C]//Proceedings of the 4th IFAC Conference on Manoeuvring and Control of Marine Craft.1997： 166-171.

[6] Bordignon K A，Durhan W C.Closed-Form Solutions to Constrained Control Allocation Problem[J].Journal of Guidance，Control，and Dynamics，1995，18(5)： 1000-1007.

[7] Buffington J M，Enns D F.Lyapunov Stability Analysis of daisy Chain Control Allocation[J].Journal of Guidance，Control，and Dynamics，1996，19(6)： 1226-1230.

[8] Buffington J M，Enns D F，Teel A R.Control Allocation and Zero Dynamics[J].Journal of Guidance，Control，and Dynamics，1998，21(3)： 458-464.

[9] Bolender M A，Doman D B.Nonlinear Control Allocation Using Piecewise Linear Functions[J].Journal of Guidance，Control，and Dynamics，2004，27(6)： 1017-1027.

[10] Petersen J A M，Bodson M.Interior-Point Algorithms for Control Allocation[J].Journal of Guidance，Control，and Dynamics，2005，28(3)： 471-480.

[11] 杨恩泉，高金源，李卫琪.多目标非线性控制分配方法研究[J].航空学报，2008，29(4): 995-1001.

[12] Bodson M.Evaluation of Optimization Methods for Control Allocation[J].Journal of Guidance，Control，and Dynamics，2002，25(4)： 703-711.

[13] Page A B，Steinbergt M L.A Closed-loop Comparison of Control Allocation Methods[C]//AIAA Guidance，Navigation，and Control Conference and Exhibit.2000.

[14] Page A B，Steinberg M L.High-fidelity Simulation Testing of Control Allocation Methods[C]//AIAA Guidance，Navigation，and Control Conference and Exhibit.2002.

[15] Oppenheimer M W，Doman D B.Methods for Compensating for Control Allocator and Actuator Interactions[J].Journal of Guidance，Control，and Dynamics，2004，27(5)： 922-927.

[16] Oppenheimer M W，Doman D B.A Method for Compensation of Interactions Between Second-Order Actuators and Control Allocators[C]//Proceedings of the IEEE Aerospace Conference,2005.

[17] Härkegåxd O.Dynamic Control Allocation Using Constrained Quadratic Programming[J].Journal of Guidance，Control，and Dynamics，2004，27(6)： 1028-1034.

[18] Luo Y，Serrani A，Yukovich S， et al.Model Predictive Dynamic control Allocation with Actuator Dynamics[C]//Proceeding of the 2004 American Control Conference,2004： 1695-1700.

[19] Luo Y，Serrani A，Yukovich S， et al.Dynamic Control Allocation with Asymptotic Tracking of Time-varying Control Input Commands[C]//American Control Conference,2005： 2098-2103.

[20] Luo Y，Serrani A，Yurkovich S， et al.Model-Predictive Dynamic Control Allocation Scheme for Reentry Vehicles[J].Journal of Guidance，Control，and Dynamics，2007，30(1)： 100-113.