神经网络与加权模糊马尔可夫链的组合模型及其应用*

2013-05-14王江荣李向兵

计量技术 2013年10期

王江荣李向兵

(甘肃兰州石化职业技术学院信息处理与控制工程系，兰州 730060)

0 引言

全国粮食产量与有效灌溉面积、农业基本建设投资和劳动力投入等诸多因素有着很强的关联性[1]。受气象条件的多样性、变异性、复杂性以及土地流失等因素的影响，粮食产量存在着大量的不确定性、不稳定性，以及较强的随机性、相依性和非线性，从而降低了产量预测的精确性。因此，有必要研究在存在大量不确定因素的情况下，如何较为准确地预测全国粮食产量，为有关部门提供决策依据。

该文提出了一种基于BP(Back Propagation)神经网络与加权模糊马尔可夫链的组合预测方法。首先采用BP神经网络，使用较少的样本数据完成粮食产量曲线的粗略拟合，在此基础上应用模糊聚类方法计算出粮食产量数据序列的分级模糊区间[2]，然后以产量序列规范化后的各阶自相关系数为权，用加权的马尔可夫链缩小预测区间以提高预测精确度，从而为定量评估多重因素对粮食产量影响提供了一种新的思路。

1 BP神经网络与加权模糊马尔可夫链组合预测模型的构建

1.1 基于BP神经网络的动态基准曲线拟合

神经网络作为一种并行的运算模型，能够在被建对象结构及参数未知的情况下，通过样本训练，自适应地获取输入与输出的非线性映射关系[3]。BP神经网络结构简单，具有较强的非线性映射能力，是应用最为广泛的一类多层前向神经网络。BP学习算法是一种梯度快速下降法，其训练过程可归纳如下：

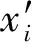
(1)

该网络参数确定：

1)输入层、隐层和输出层的节点数；

2)学习率和动量；

3)成本函数或训练样本数量的最大允许平方误差。

随后对人工神经网络ANN(Artificial Neural Networks，)进行训练，当误差平方值小于最大允许误差平方值时停止训练。

神经网络模型的应用前提是获取较大量的样本训练数据，如果训练样本数据不够充分,训练后的网络结构往往不完全稳定，尤其完成的后续数据组的预测通常会在一定范围内随机波动，降低了预测的精度。马尔可夫链恰能有效地预见并消除由系统随机性而产生的预测误差。因此，通过建立神经网络与马尔可夫链的组合预测模型，将二者进行优势互补,能够得到更为准确的预测结论。

1.2 加权模糊-马尔可夫链预测模型

马尔可夫链预测是基于马尔可夫过程的理论基础之上，用来研究系统状态转移规律，分析随机事件未来发展趋势及可能结果的一种预测方法[4]。马尔可夫链预测模型可表示为

X(n)=X(0)Pn

(2)

式中，X(n)为n时刻的状态概率向量；X(0)为初始时刻的状态概率向量；P为状态转移概率矩阵。

式(2)具有根据P及X(0)预测第n步的意义，预测的关键在于状态转移概率矩阵P的确定。

1.2.1 马尔可夫链状态区间的划分

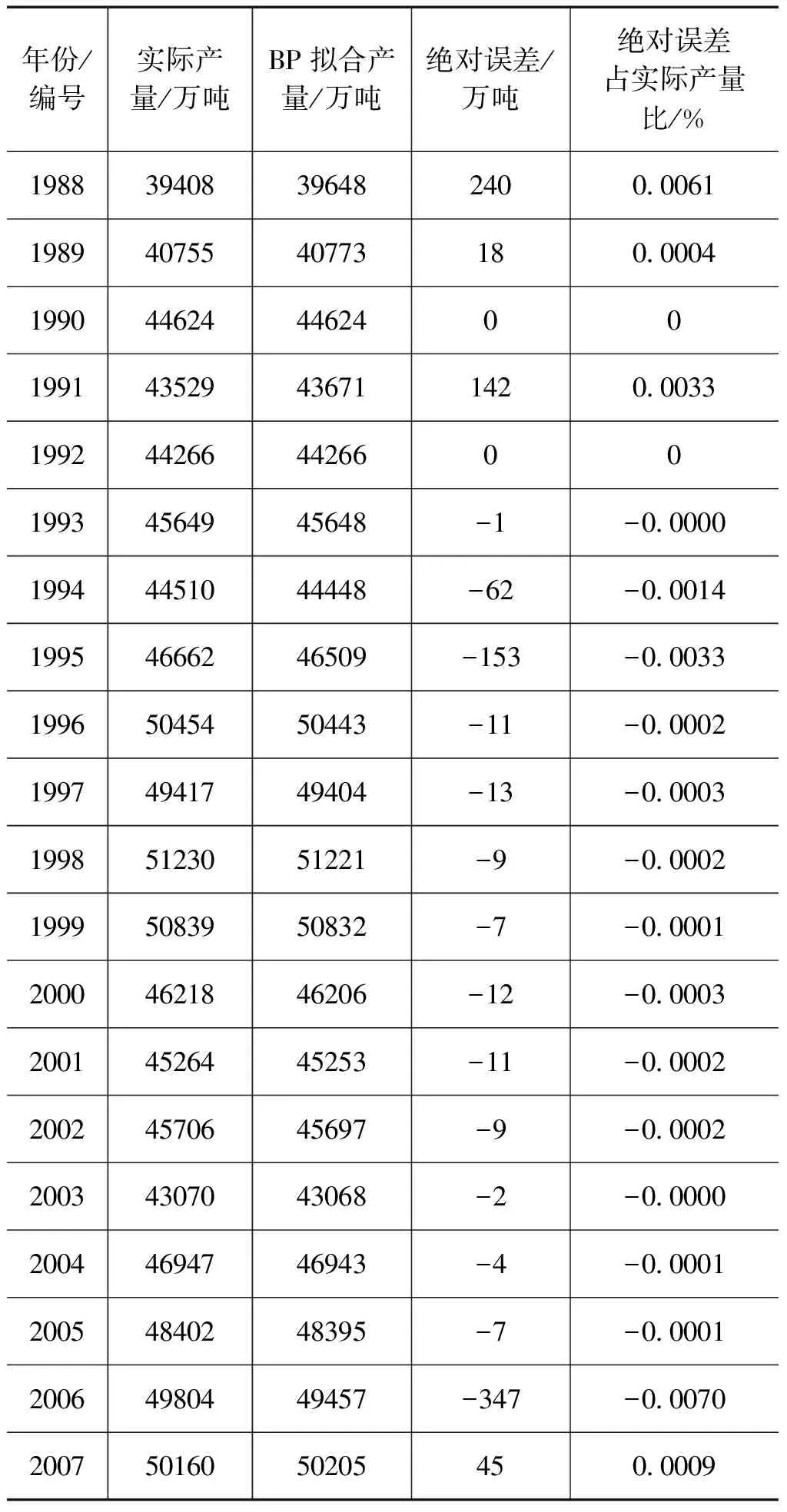
根据粮食产量样本资料，得到BP神经网络的拟合值，求出误差幅度(绝对误差占实际产量百分比)，将误差幅值数据列由小到大排列，应用模糊C均值聚类方法计算获得粮食产量数据序列的分级模糊区间，确定出马尔可夫链的状态空间，并给出历史资料数据序列中各时段粮食产量所处的模糊分级区间状态i(i=1,2,…,n)。

1.2.2 马尔可夫链转移矩阵

根据1.2.1获得的模糊分级区间数据及状态表，计算出不同步数的马尔可夫链转移概率矩阵[5-6]：

若状态i在状态表中出现的次数为Mi，由状态i经过m步转移到状态j的次数为Mij，则状态i经过m步到状态j的转移概率为

(3)

状态转移概率矩阵的构造如下：

1.2.3 马尔可夫链权值计算

由于粮食产量是一组相依的随机变量，因而可考虑先分别依其前面若干时段的数据对所求时段的粮食产量进行预测，然后按前面各时段与该时段相依关系的强弱加权求和，即在预测过程中加入权重的影响，以期能充分、合理地利用信息进行预测。

1)计算粮食产量序列的各阶自相关系数

(4)

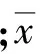
2)对各阶自相关系数进行归一化，即

(5)

将式(5)作为各种滞时(步长)的马尔可夫链的权重(m为按预测需要计算到的最大阶数)。

1.3 预测区间和预测值的确定

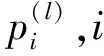
(6)

(7)

2 实例分析

2.1 数据统计

根据能够计量、具有农学意义两个原则，结合已有的研究成果[7]，本文选取1988年～2008年的粮食总量为输出因子,初步选取粮食作物播种面积、化肥施用量、粮食作物有效灌溉面积、受灾面积、农村用电量、农村机械总动力、劳动力投入、基本建设支出、农业科技三项费用、单产、农村居民家庭平均收入等11个因子构筑模型。变量及原始数据来源于中国统计局《中国统计年鉴2009》(由于占篇幅较多，在此略去)。采用灰关联分析法[8]计算出各影响因素的综合关联度，按从大到小顺序排列(取前8个)如下：

有效灌溉面积(0.97285:关联度,后同)；劳动力投入(0.76553);粮食单产量(0.75591); 成灾面积(0.66551); 农业机械总动力(0.64965);化肥施用量(0.62239)；农村用电量(0.58151)；粮食作物播种面积(0.52808)。以此8要素进行模型的构建。利用Eviews软件对所选8要素进行历史数据分析，此8要素对粮食产量有显著影响，且具有明显的多元相关性，其相关系数(决定系数)R2=0.984。所以，用本文所选8因素进行粮食产量拟合和预测完全可行，并且有较高的可信度。

2.2 基于BP神经网络的粮食产量基准曲线拟合

设定BP网络的输入层节点数为8，分别表示农业机械总动力、有效灌溉面积、化肥施用量、农村用电量、农作物播种面积、成灾面积；粮食单产量；劳动力投入。输出层节点数为1，即粮食产量；由于单隐层前馈网络具有较好的非线性映射能力，隐层数取1。按如下公式选择隐层节点数[9]。

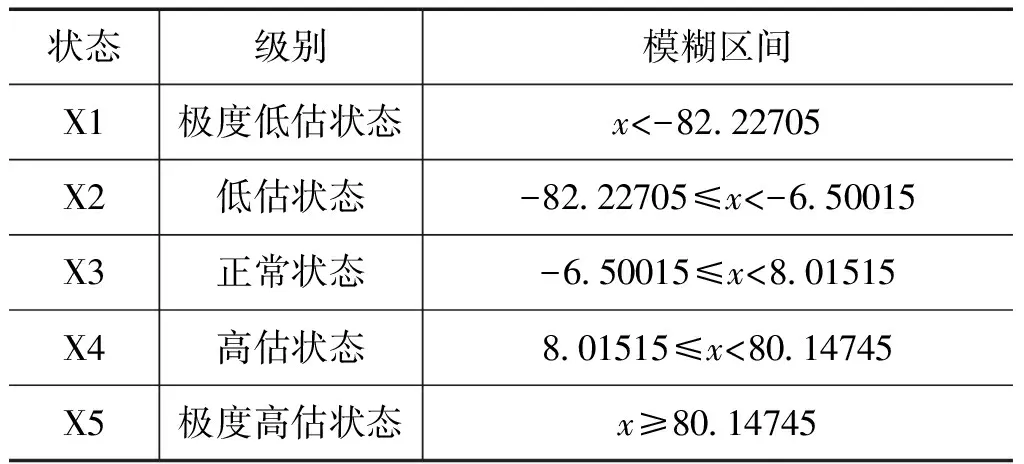
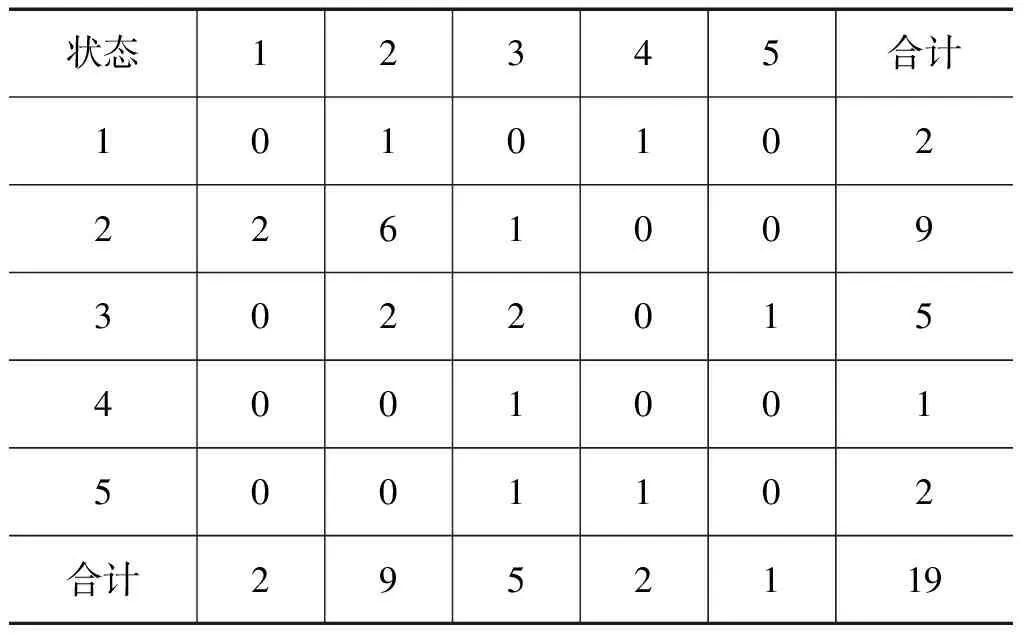
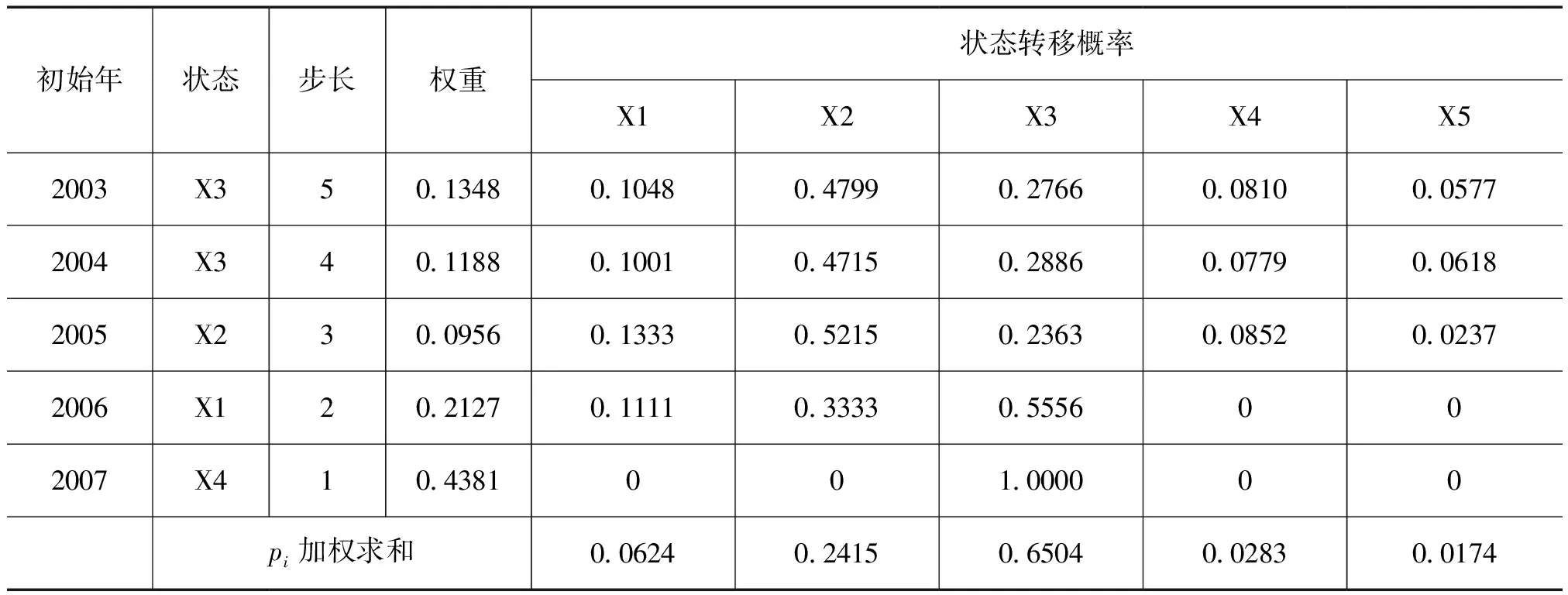
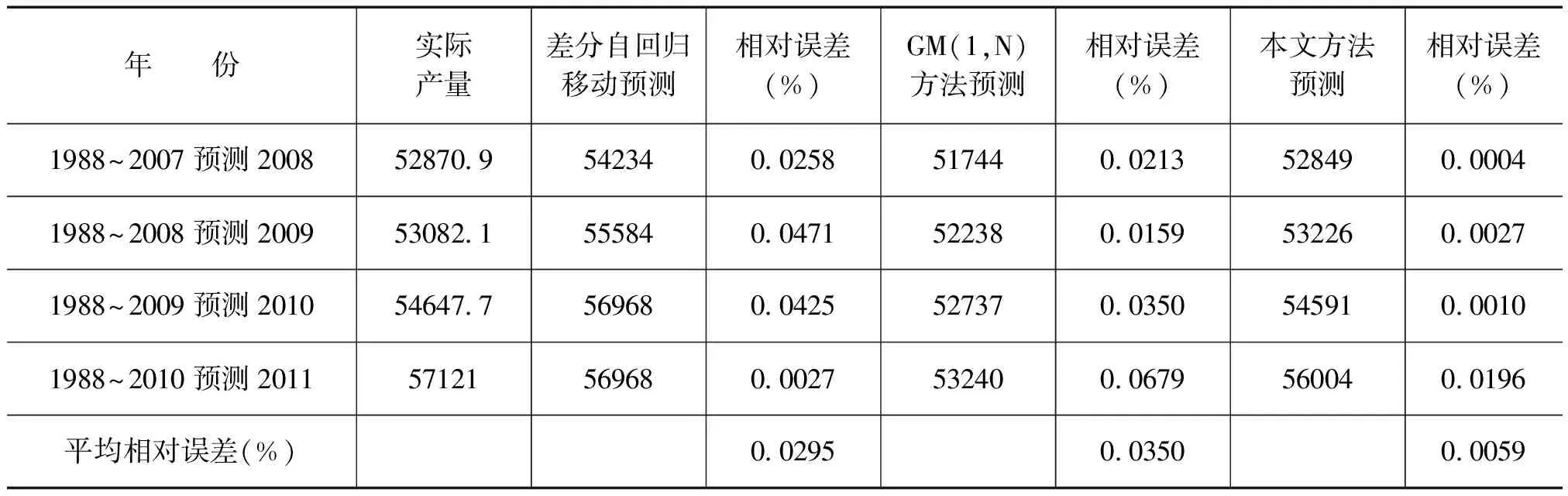
l=log2n

式中，n为输入层节点数，上述三式为经验公式,只需满足一式即可；l为隐含层节点数；m为输出层节点数；a为0～10间的常数。选代次数M0=5000，误差门限ε=0.0001，网络学习系数η取0.5，动量项系数a=0.1。训练样本为1988年～2007年的20个样本，检测样本为2008年～2011年4个独立样本。采用MATLAB软件及文献[7]中的BP神经网络程序经过算法学习和筛选，得到最优化的BP神经网络结构8-5-1(输入层节点—隐含层节点—输出层节点)。

使用训练样本数据建立预测模型，并对1988年～2007年的粮食产量进行内预测，内预测结果见表1，可以看出拟合得非常好，有较高的精确度。

2.2 基于模糊C均值聚类法的模糊分级区间

对由BP网络算法得到的表1中误差幅值(绝对误差)采用模糊C均值聚类[10]，求出粮食产量数据序列的分级模糊区间。经检验，误差幅值划分为5个模糊分级区间比较合适(相对分3类、分4类误差最小,且误差收敛于0.0215)，即马尔可夫链有5个状态。具体划分见表2。

表11991年—2010年粮食产量的实际值及BP网络计算拟合值

表2粮食产量数据列模糊分级区间(x为绝对误差)

由表1和表2知：

1)出现在状态1的编号为：1995和2006；

2)出现在状态2的编号为：1994、1996、1997、1998、1999、2000、2001、2002和2005；

3)出现在状态3的编号为：1990、1992、1993、2003和2004；

4)出现在状态4的编号为：1989和2007；

5)出现在状态5的编号为：1988和1991。

2.3 基于BP预测结果的马尔可夫状态转移矩阵

根据2.2的分析结果可得1988年～2007年粮食产量预测结果的马尔可夫状态转移表，如表3所示。

表31989年～2008年粮食产量预测结果的马尔可夫状态转移表

由表3可确定马尔可夫链状态转移概率矩阵P：

(8)

式(2)可看成齐次马氏链，所以由C—K方程[11]得到一步到五步的转移概率：

P1=P，P2=P2，P3=P3，P4=P4，P5=P5

(9)

2.4 2008年～2011年粮食产量预测

用1988年～2007年20个样本作训练样本建模，预报2008年；再用1988年～2008年21个样本作训练样本建模，预报2009年；依此类推，直到用1988年～2010年23个样本作训练样本建模，对2011年进行预报。

根据表1(1988年～2007年)和式(4)并利用软件SPSS.13求出粮食产量数据序列的各阶自相关系数分别为

r1=0.631，r2=0.306，r3=0.138，r4=-0.171，r5=-0.194。

将各阶自相关系数规范化后得到各步数的马尔可夫链的权重(见式(5))：

ω1=0.43814，ω2=0.21268，ω3=0.09561，ω4=0.11875，ω5=0.13482

由1.3及式(6)得表4。

表42008年粮食产量预测表

由表4可知，max{pi}=0.6504，i=3，即2008年粮食产量的预测值状态为X3(正常状态)。根据模糊区间求得2008年的产量预测区间为[52842,52857]，取中间值，即为52849(万吨)，实际产量为52870.9(万吨)，相对误差0.04%。

同理，得到2009年～2011年的粮食产量的预测值区间分别为[51919，54532]，[53280，55902]，[54687，57320]，其中间值分别为：53226(万吨)，54591(万吨)，56004(万吨)。

3 三种方法结果比较分析

为了检验新模型方法的预测性能，我们分别采用差分自回归移动平均模型[1]、灰色GM(1,N)模型对2008年～2011年粮食产量进行了预测,并与本文预测结果比较，有关数据见表5。

表5三种模型对2008～2011年检测样本逐年预测结果误差比较 (单位：万吨)

表5数据表明，本文预测方法的预测精度远好于其它两种方法。本文方法的优点在于充分发挥了BP网络的多变量处理能力及网络适应能力。另外，随着预报对象序列的逐年增加，资料数据的代表性也日益增强，自相关系数、状态转移概率矩阵、权重值也随之发生变化，将每年预报对象的新的实测值加入到资料分析系列中，实现了在线调整预报对象的自相关系数、状态转移概率矩阵和权重，从而提高了预报的精度。