智能变电站线性插值同步性研究及工程实践
2013-05-11高振东许永金倪维东邵灿辉
高振东,许永金,倪维东,邵灿辉
(南京河海南自水电自动化有限公司,南京 210032)
智能变电站线性插值同步性研究及工程实践
高振东,许永金,倪维东,邵灿辉
(南京河海南自水电自动化有限公司,南京 210032)
0 引言
由于电子式互感器具有体积小、精度高、抗干扰能力强、不饱和、可靠、集成、低碳、环保等特点,近年来得到了大力推广和应用,电子式互感器的应用和智能变电站的建设不可避免的要接入不同间隔、不同厂家的IED设备。使得间隔层IED设备的各个通道的采样数据,不可避免的存在不同步的问题,基于FPGA的插值同步算法由于FPGA(可编程门阵列)具有快速性、可并行性、延时固定性等特点通过软件的方式实现采样同步,并且同步后二次采样数据能够满足IEC6044-8等标准的精度要求。
1 插值算法及其原理
根据香农定理,信号的重建是对样本进行插值的过程,即,从离散的样本中,用数学的方法确定连续信号。
其系统图如图1所示,Xa(t)为模拟信号,Ya(t)为重建数据,P(t)为采样函数。
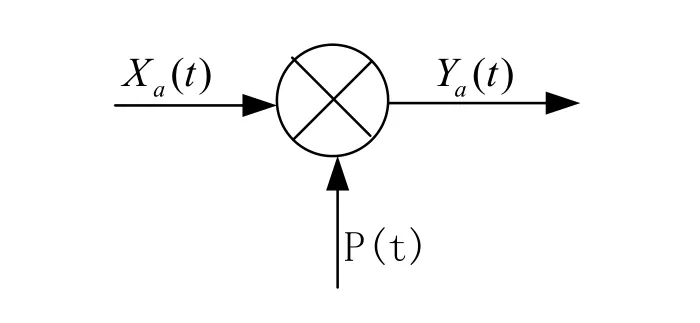
图1 插值系统图
假设模拟信号经过理想采样得到,则理想插值数据公式为:
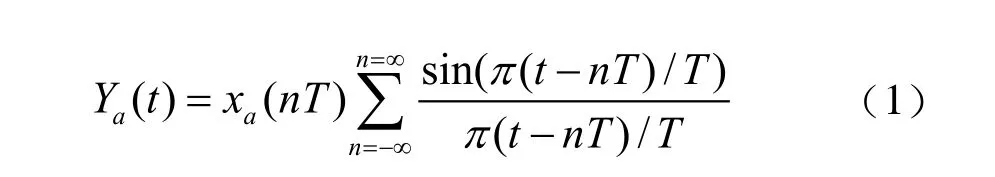
其中,xa(nT)为离散采样值,xa(t)为模拟信号,T为采样周期。
式(1)由于是理想采样信号可以完全重建,然而在实际应用中采样回路很难达到理想的采样效果,所以采用软件插值算法是一种比较理想的处理方式。
2 线性插值算法
假设我们已知坐标(x0,y0)与(x1,y1),要得到[x0,x1]区间内某一位置x在直线上的y值。根据图2中所示,我们得到:
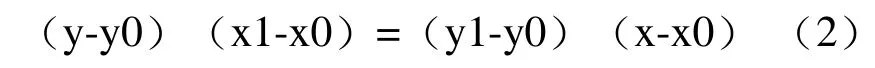
假设方程两边的值为α,那么这个值就是插值系数—从x0到x的距离与从x0到x1距离的比值。由于x值已知,所以可以从公式得到α的值:
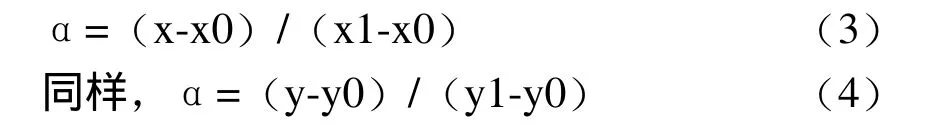
这样,在代数上就可以表示成为:
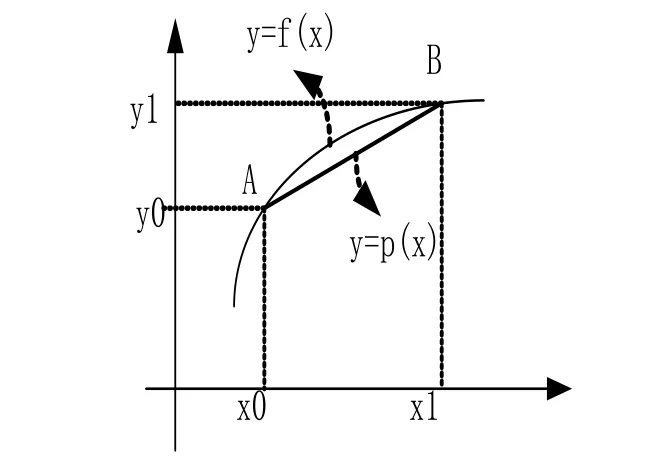
图2 插值算法图
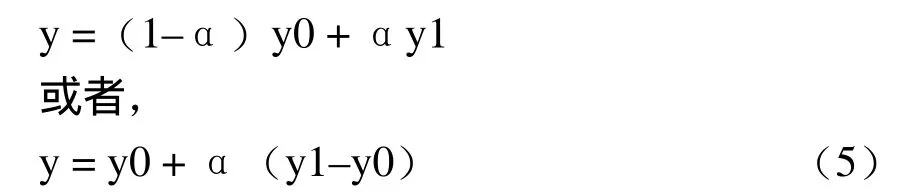
这样通过α就可以直接得到 y。实际上,即使x不在x0到x1之间并且α也不是介于0到1之间,这个公式也是成立的。
由此,可得出线性插值可以插出连续信号,其精度随着插值点的密度(即x1–x0)无限趋近于零时,越接近于实际的采样值。而采样频率的增加,会占用CPU更多的资源等,成本可能会有所增加,所以选则合适的采样频率,同样能够满足变电站的需要。
3 某变电站主变保护插值同步工程实践
2010年12月安徽某220kV变电站在空载冲击变压器5次后,进行带负荷向量试验。主变保护以A相(所有显示以A相电流为基准,另外幅值基本没有任何变化故不再体现)为例显示如表1所示。

表1 高低压侧A相电流电压角度
由于低压侧为容性负载(低压侧只带了电容器)所以电流应滞后电压90°如表1而实际上按照向量低压侧电流滞后低压侧电压300°-224°=76°;所以,产生了90°-76°=14°的角差。
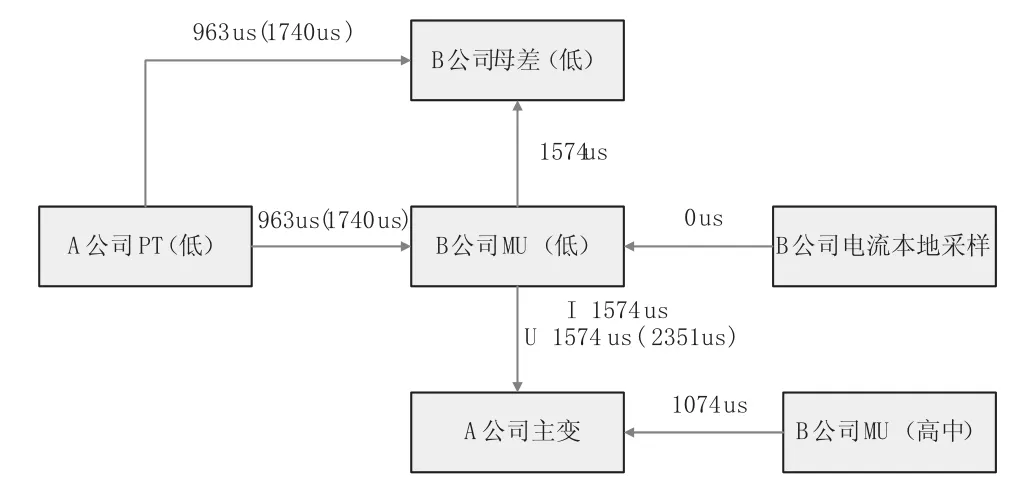
图3 实际接线示意图
对以上问题分析如下,主变低压侧存在电流电压角差不对的问题,主要是由于A公司MU和B公司MU的采样值延时不一致导致,目前主变低压侧各个运行装置的延时分布情况如图4所示。
图3中的963us为A公司MU发送IEC60044-8报文中自带的延时参数(并不是实际物理延迟时间),1740us为A公司MU采样值的实际延时参数,1574us为B公司MU报文中自带实际物理发送延时参数,2351us为B公司MU发送电压采样值的实际延时参数。
1)电压滞后问题解析
低压侧电压延时T1:2351us = 1574us+ 1740us– 963us。
高压侧电压延时T2:1074us。
2)单间隔电流电压角差解析
理论计算:
低压侧电压实际延时T1:2351us。
低压侧电流实际电流延时T2:1574us。
由于为360°对应的时间为0.02s=20000us。
所以电流电压对应角差:(2351us – 1574us)×1.8°/100 = 14°与实际角差吻合。
3)高低压侧电流角差解析
对于主变差动由于高低压侧接线为星角-11点钟接线高低压侧理论角差应为:IHA=0°,ILA=210°。
主变显示角度如表1为:IHA=0°,ILA=224°。
高低压侧电流理论与实际角差为224°-210°= 14°。
理论计算角差为:(1574-1074)×1.8°/100=9°。
由于解决电压滞后问题时,低压侧通道采样值角度提前了(2351 – 1074)×1.8/100 = 23°,所以实际显示角差应为23°-9°= 14°,与实际显示角差相吻合。
根据以上分析,出现角差的原因为B公司MU实际送至主变的采样值电流电压存在14°角差。
4)解决方法
如图4所示,A公司主变保护自己从母线MU获取母线电压,只从只从B公司MU获取电流信号。该方案涉及以下四个方面的修改:
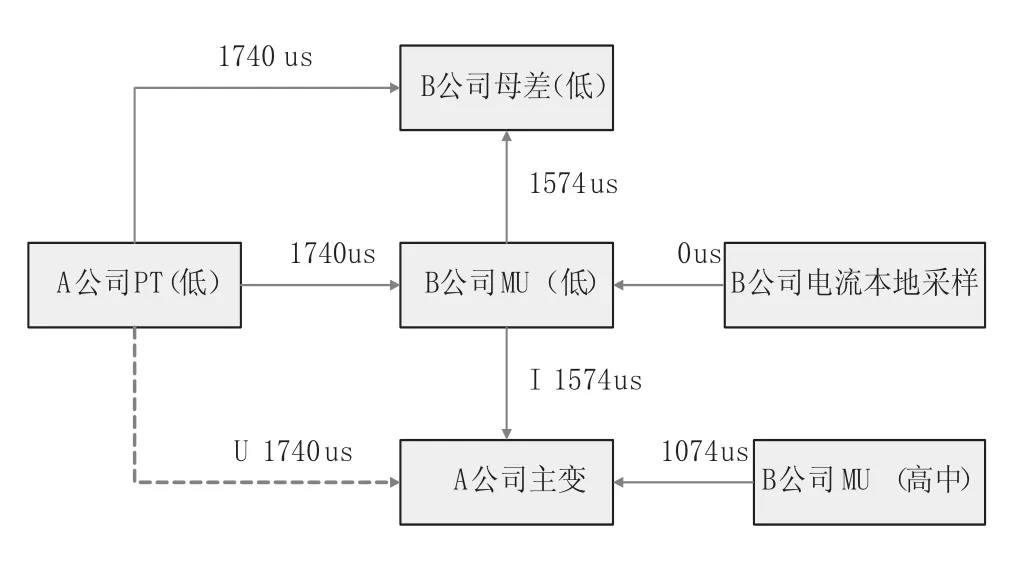
图4 更改后接线示意图
(1)增加A公司MU至A公司主变的光缆;
(2)更改A公司MU的延时参数(以实际延时1740us为基准)并增加至主变的通信链路;
(3)更改B公司MU需程序,以适应A公司MU的实际延时时间参数,并进行插值计算;
(4)更改A公司主变数据集中器的同步时刻点,以不同MU的电流、电压最迟延迟时间为参考点插值同步。
通过插值同步算法后主变保护显示值如表2完全满足差动保护要求。

表2 高压侧、低压侧A相电流电压角度值
4 结论
综上所述,从以上工程实践中可以看出,线性插值同步算法虽然简单、导数不连续。但是,在选取得当插值点时完全能够满足变电站对采样精度的要求。同时该方案还适用于IEC61850-9-2的点对点方案,也同样适用于跨间隔的母差等保护。
[1]曹团结,陈建玉,黄国方.基于IEC 61850-9的光纤差动保护数据同步方法.
[2]乔洪新,黄少锋,刘勇.基于二次插值理论的电子式互感器数据同步研究.
[3]徐光辉,李友军,王文龙,熊慕文.数字化变电站IED采样数据同步插值的设计.
[4]IEC6044-7 Instrument transformers:Part 7.
[5]IEC6044-8 Instrument transformers:Part 8.
[6]王洪帅,徐青山,袁宇波,等.智能变电站非对称式光纤差动保护同步性测试方法 .
The research and engineering practice base on linear and synchronization interpolation about smart grid
GAO Zhen-dong,XU Yong-jin,NI Wei-dong,SHAO Can-hui
采用电子式互感器IED继电保护设备可靠性依赖于采样的同步性,本文论述了采样值点对点插值线性同步算法,插值算法能够满足保护以及测量等变电站系统的精度要求。结合某变电站主变保护插值成功的方案,根据各方案的优缺点,选择合适的插值方案达到事半功倍的效果。
电子式互感器;线性插值;FPGA;工程实践
高振东(1979-),男,工程师,研究方向为电力系统及智能水电厂自动化。
TM64
B
1009-0134(2013)01(下)-0106-03
10.3969/j.issn.1009-0134.2013.01(下).30
2012-08-08
