解决多重共线性的新思路:路径分析
2013-05-10李从欣张再生李国柱
李从欣,张再生,李国柱
(1.天津大学管理学院,天津 300072;2.石家庄经济学院 经济系,石家庄 050031)
0 引言
随机项满足高斯假设的回归模型称为经典线性回归模型。当经典假设不成立时,最小二乘估计量通常不再适用,需要采用其他的估计方法。基本假设违背主要包括:随机项存在异方差,随机项存在序列相关,解释变量之间存在共线性,解释变量是随要变量用与随机项相关。在以上几种情况中,异方差、序列相关、随机解释变量模型等都有较好的解决方案,而多重共线性到目前为止尚没有非常好的解决方法,本文将路径分析引入多重共线性模型,作为解决多重共线性的一种思路,供大家参考。
1 多重共线性回顾
在回归模型中,如果某两个或多个解释变量之间出现了相关性,则称为存在多重共线性。多重共线性包括完全多重共线性和近似多重共线性,在实际经济统计数据中,完全多重共线性极为少见,一般出现的是近似共线性。
多重共线性产生的原因很多,主要有:①某些经济变量本身存在某种共同的变化趋势;②将某些解释变量的滞后变量引入模型作为解释变量;③多重共线性更多的情况是由于样本数据呈现出来的,并不是解释变量之间本身存在多重共线性。
当共线性严重时,会造成以下后果:参数估计值不精确,也不稳定,样本数据稍有变化,都会使估计值发生较大变化;参数估计量的方差较大,使参数的显著性检验增加了接受零假设的可能;难以区分每个解释变量的单独影响。
检验解释变量之间是否存在严重多重共线性的常见方法包括:①相关系数检验法,即通过计算解释变量两两之间的相关系数来判断是否存在多重共线性,但它只能用来检验两个解释变量之间是否存在相关关系,不能检验多个解释变量之间是否存在多重共线性。②辅助回归模型检验法,即建立每一个解释变量与其余解释变量的辅助回归模型来检验多重共线性,当辅助回归方程拟合程度较高时,说明模型存在高度多重共线性。③方差膨胀因子法,一般认为当方差膨胀因子大于5或10时,认为模型存在严重的多重共线性。
如果经过检验证明模型存在多重共线性,就应采用必要的措施进行补救,常用的处理方法包括以下几种:①保留重要的解释变量,去掉次要的或可替代的解释变量;②利用先验信息改变参数的约束;③对原始变量进行差分;④逐步回归法⑤采用有偏估计量,如偏最小二乘法、岭回归法、主分量回归。以上方法中,使用比较多的是逐步回归。
路径分析同样可以解释多重共线性问题,尤其是其在模型设立时即考虑了解释变量的相关性。
2 解决多重共线性的新思路:路径分析
路径分析模型是反映多个变量之间关联或储存关系的模型。根据变量之间关系的类型可以分为递归和非递归两类[1]。递归模型中不含有相互影响的变量,即路径图中没有双向箭头,无反馈作用;非递归模型则含有相互影响的变量,路径图中允许存在双向箭头。和线性回归分析相接近的是非递归模型,非递归模型路径图的一般形式如图1所示:
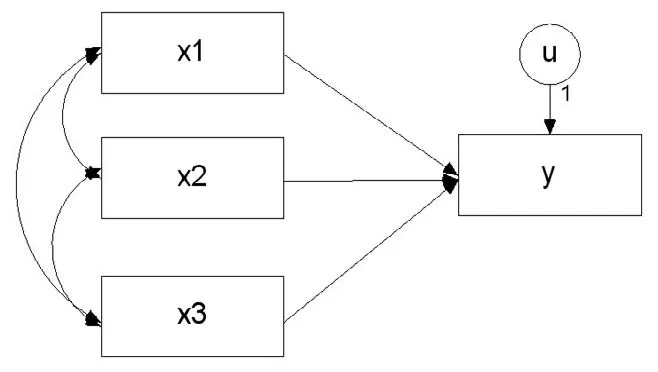
图1 非递归模型的路径图
在图1中,双箭头表示变量之间的相关关系,u与解释变量之间不用双向箭头连接,表示随机项与解释变量不相关。由图1可以看出,非递归模型可以写成以下形式:
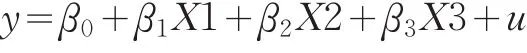
此模型形式和多元线性回归模型完全相同,但模型的假设条件却有所不同。非递归模型的假定条件包括:
(1)y为服从多元分布的随机变量
(2)解释变量X无测量误差
(3)u是服从均值为0,方差为常数的多元分布的随机变量,且与X不相关
由以上假定可以看出,非递归模型的假定条件和多元回归模型的假定非常相似,所不同的是非递归模型并不要求解释变量之间不相关。因此多元线性回归模型可以看作是非递归模型的一种特殊形式。
除此之外,路径分析和线性回归分析的求解原理也不相同,线性回归不管是采用最小二乘法或最大似然法,最后都归结到使残差平方和最小;而路径分析则基于样本协方差进行求解,其基本思想是,观测变量的协方差矩阵是一组待估计参数的函数,如果模型是正确的,那么总体的协方差矩阵就能够被准确地重复出来。因此,路径分析不能以传统的统计分析软件估计,只能以结构方程分析软件进行分析。以结构方程分析软件进行路径分析,可以避免多次决策带来的错误,同时也可以获得更为丰富的统计信息[2]。
3 路径分析解决多重共线性的的实证
为了对路径分析解决多重共线性的效果进行验证,我们采用李子奈教授所著《计量经济学(第二版)》中的例子,该例子选用了影响粮食生产(Y)的五个主要因素,农业化肥施用量(X1)、粮食播种面积(X2)、成灾面积(X3)、农业机械总动力(X4)、农业劳动力(X5),其中,成灾面积的符号为负,其余均应为正。具体数据如表1所示:
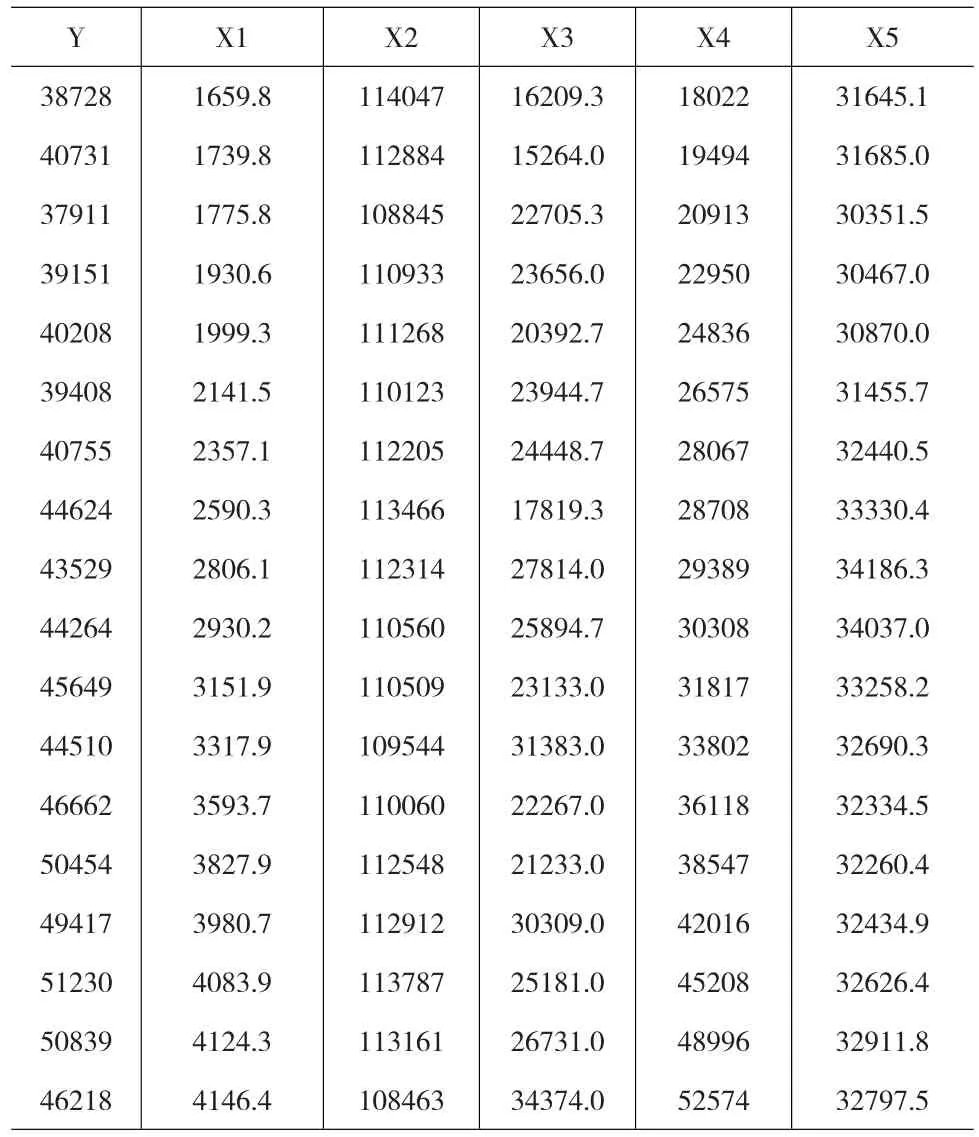
表1 中国粮食生产与相关投入资料
该书中已分别采用最小二乘法和逐步回归法进行了估计。最小二乘法的估计结果如下:
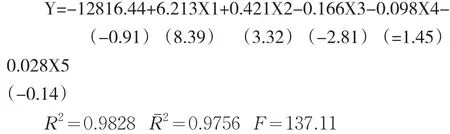
由于R2较大且接近于1,且F统计量显著,故认为粮食生产与上述解释变量间总体线性关系显著。但由于其中X4、X5的参数估计值未能通过t检验,且符号的经济意义也不合理,故认为解释变量间存在多重共线性。
逐步回归的最优估计结果如下:

最优估计结果表明,由于多重共线性,X4与X5是多余的。
接下来本文采用路径分析估计多重共线性模型,该模型的初始路径分析图如图2所示:
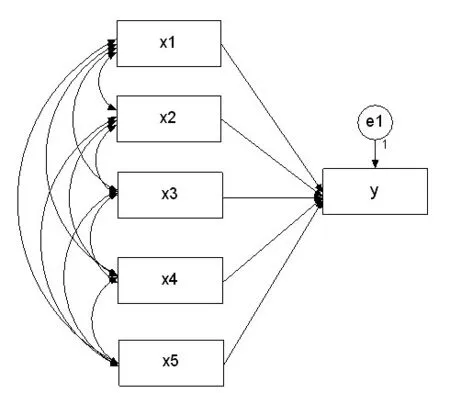
图2 粮食生产函数的路径分析图
对该模型进行估计,回归系数及检验结果见表2。
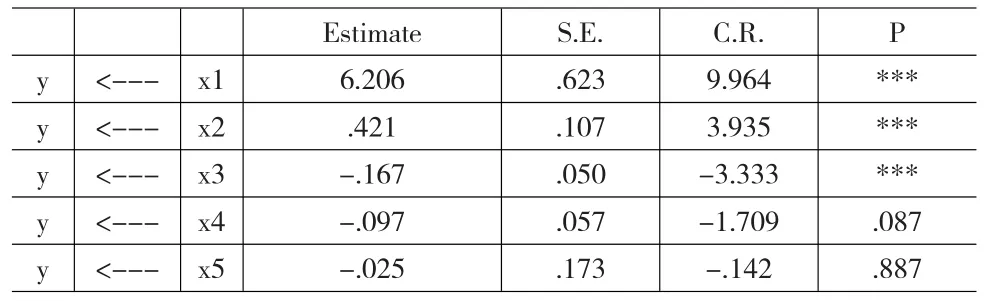
表2 回归系数表
由表中估计值及检验结果可以看出,X4、X5对粮食生产的影响不显著,且符号的经济意义也不合理,可以考虑删掉这两个变量。
各变量间的协方差矩阵如表3所示:
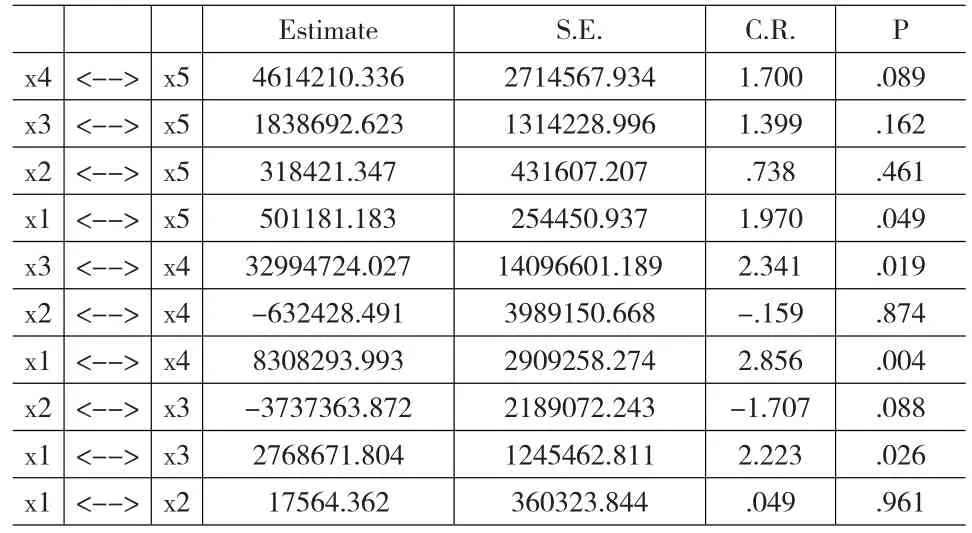
表3 各变量间协方差矩阵
由表3检验结果可知,X3与X5、X2与X5、X2与X4、X1与X2至少在0.10的显著性水平下不显著,因此删掉这几对因果关系,修改后的路径图如图3所示:
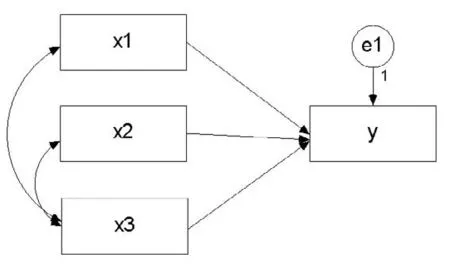
图3 修改后的路径图
对修改后的路径图进行极大似然估计,其中截距为-11978.18,p-value为0.348,因此截距项不显著。其他回归系数及检验结果见表4:
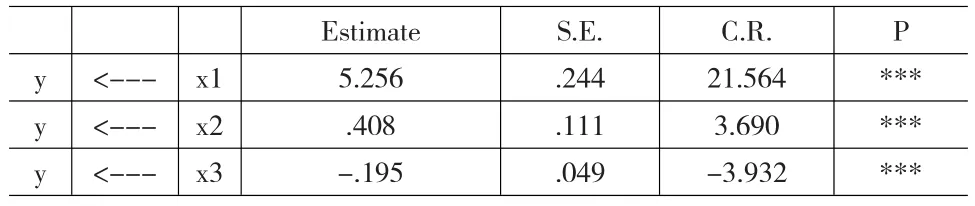
表4 修改模型的回归系数表
从表4可以看出,三个解释变量对粮食生产的影响均显著,且符号也符合预期。
各变量间的协方差矩阵如表5所示:

表5 修改模型的协方差矩阵
从表5可知,X1与X3、X2与X3的协方差在0.05的显著性水平下都是显著的。
从模型的整体拟合上来看,卡方值为0.002,P值为0.961,表明观察数据支持理论模型;RMSEA为0,NCP为0,表明模型完全适配;NFI、RFI均等于0,IFI为1.012,TLI为1.078,CFI为0,表明模型适配度相当完善。综合以上指标,我们建立的理论模型无论从整体拟合上,还是从参数检验上都是一个非常完美的模型。
最后我们将路径分析结果写成模型形式:
Y=-11978.18+5.256X1+0.408X2-0.195X3
如果路径系数取两位小数的话,我们会发现,这个结果与逐步回归的结果完全相同。因此采用路径分析法解决多重共线性问题具有良好的效果。
[1]易丹辉.结构方程模型方法与应用[M].北京:中国人民大学出版社,2008.
[2]赵守盈.矩结构分析模型[M].广州:暨南大学出版社,2011.
[3]李子奈.计量经济学(第二版)[M].北京:高等教育出版社,2005
