TOPSIS-AHP方法在城市综合实力评价中的应用

王积建

（浙江工贸职业技术学院 基础部，浙江 温州 325003）

0 引 言

多指标综合评价是实践中经常遇到的一种决策问题，合理地确定评价指标的权重是多指标综合评价的关键。文献[1]提出了多指标综合评价的TOPSIS方法，就是将实际方案中各个指标的最优值和最劣值构造为正理想方案和负理想方案，形成两个虚拟方案，然后测度实际方案与正理想方案和负理想方案的距离，并计算实际方案与正理想方案的贴近度，贴近度越大表示方案越优，从而实现了对方案的评价及排序。虽然TOPSIS方法是一种简便易行的统计方法，但并没有提供权重如何确定，所以在实际应用中受到限制。文献[2]提出在TOPSIS方法中引入层次分析法（AHP）来确定权重。层次分析法被广泛应用于多指标综合评价的权重确定中[3-5]，但该方法带有主观性，使得评价结果缺乏客观性，在实际应用中受到限制。于是不少学者尝试在层次分析法中减少或消除主观性，文献[6]提出了改进层次分析法，力求消除主观性，但这种方法也具有明显的缺陷。

通过分析文献[6]中的改进层次分析法的缺陷，提出一种更加合理的方法——TOPSIS-AHP方法，并将其应用于城市综合实力评价中以验证其合理性。

多指标综合评价问题的一般描述为：设有m个方案A1,A2,…,Am，构成方案集A，每个方案有n个指标C1,C2,…,Cn，构成指标集C，xij为方案Ai在指标Cj下的表现值，其中，i=1,2,…,m，j=1,2,…,n，xij＞0。于是初始化决策矩阵为。现对m个方案A1,A2,…,Am进行综合评价并排序。

1 改进层次分析法确定权重的缺陷分析

基于以上分析，本文提出改进的方法，就是在确定正理想方案和负理想方案之前，先将初始化决策矩阵进行一致化、无量纲化处理。

2 多指标的标准化处理

其中，效益型指标、成本型指标、适中型指标、区间型指标的标准化公式分别为：

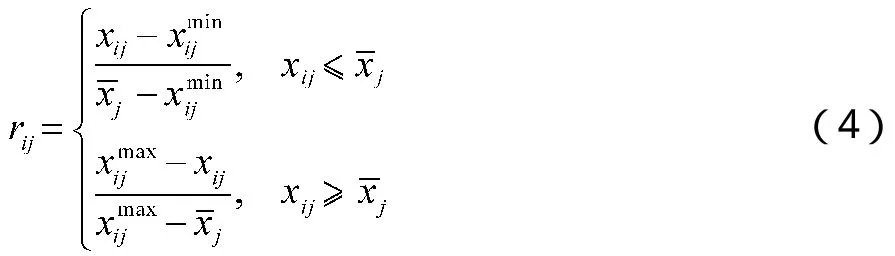
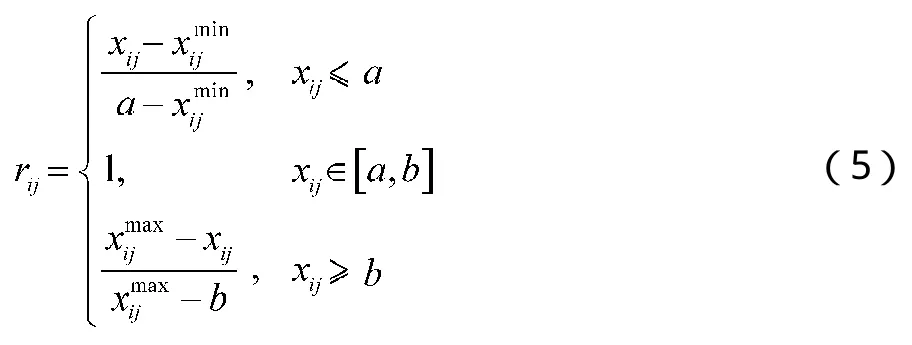
3 基于TOPSIS-AHP方法确定权重

基于TOPSIS-AHP方法确定权重的步骤如下：

（1）确定正理想指标向量C+和负理想指标向量C-。令

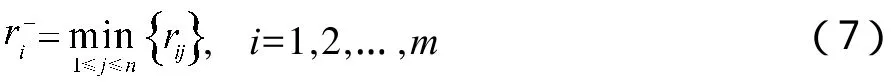
则正理想指标向量C+和负理想指标向量C-分别为，。其中，表示方案Ai在正理想指标向量C+上的标准化值，表示方案Ai在负理想指标向量C-上的标准化值。

（2）计算指标Cj=(r1j,r2j,…,rmj)T到正理想指标向量C+的距离和负理想指标向量C-的距离分别为：

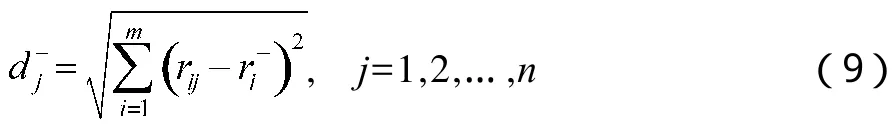
n个指标的正理想距离向量和负理想距离向量分别为,。

（3）计算指标Cj=(r1j,r2j,…,rmj)T到正理想指标向量C+的贴近度为：

n个指标的贴近度向量为d=(d1,d2,…,dn)。

其中，

（5）对判断矩阵S的每一列归一化，得归一化矩阵。其中，

（7）将V归一化得权重矩阵W=(w1,w2,…,wn)T。其中，

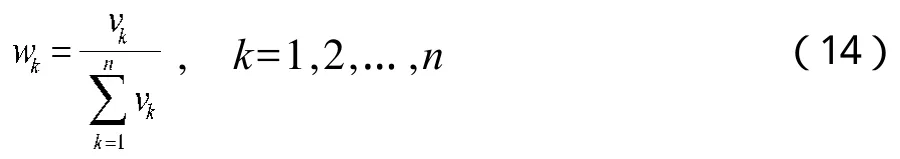
4 建立线性加权综合评价模型

方案Ai的综合评价值为：

m个方案的综合评价值向量为Z=(z1,z2,…,zm)T。综合评价值越大表示方案越优，于是可以根据所有方案综合评价值的大小进行排序。

5 应用实例

为便于比较，选取文献[6]的数据，对我国16个中心城市的综合实力做出评价并排序。文献[6]的原始数据见表1。

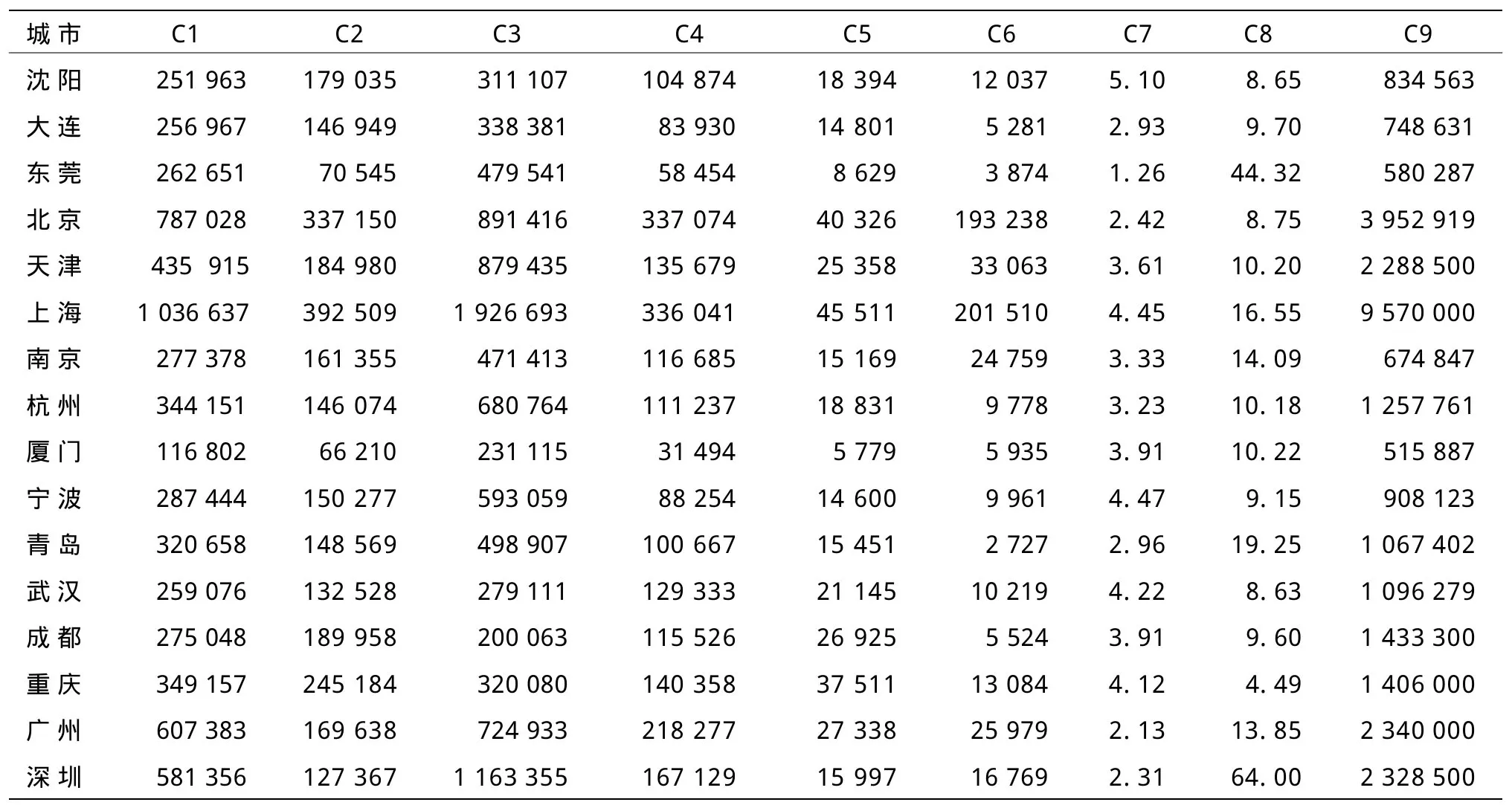
表1 我国16个中心城市各指标数据

（1）利用（2）、（3）、（4）式对表1数据进行标准化处理，标准化时取为中位数，得到标准化数据（见表2）。

（2）由（6）、（7）式求得正理想指标向量和负理想指标向量分别为：

C+=（0.7298,0.9140,1,1,0.9998,1,0.9275,0.9982,0.9994,0.8175,0.8316,0.7263,0.8965,0.7987,0.9320,0.7266）

C-=（0,0.0128,0.0058,0.3796,0.1526,0.1693,0.0176,0.0355,0,0.0364,0,0.0377,0,0,0.1170,0）

（3）由（8）、（9）式求得正理想距离向量和负理想距离向量分别为：

d+=（2.5272,2.4271,2.7650,2.3906,2.2413,3.1231,2.0441,1.2830,3.0855）

d-=（1.2610,1.3752,1.1305,1.4528,1.6476,1.0218,1.8521,2.9719,0.8758）

（4）由（10）式求得贴近度向量为：

d=（0.3329,0.3617,0.2902,0.3780,0.4237,0.2465,0.4754,0.6985,0.2211）

（5）由（11）式求得互反判断矩阵为：

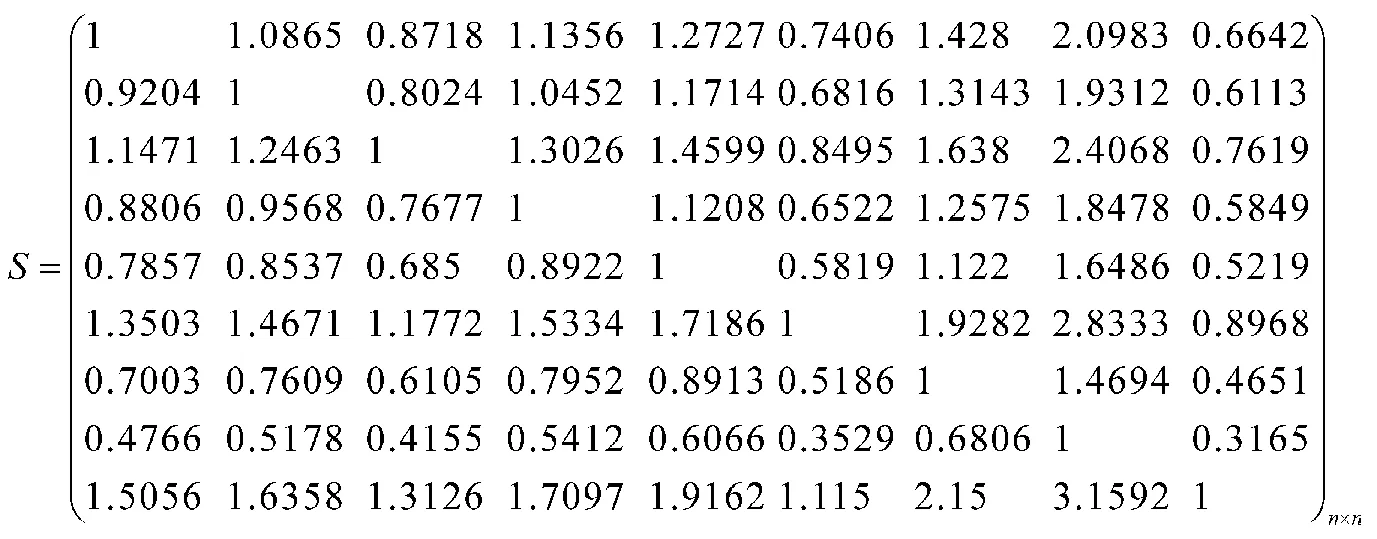
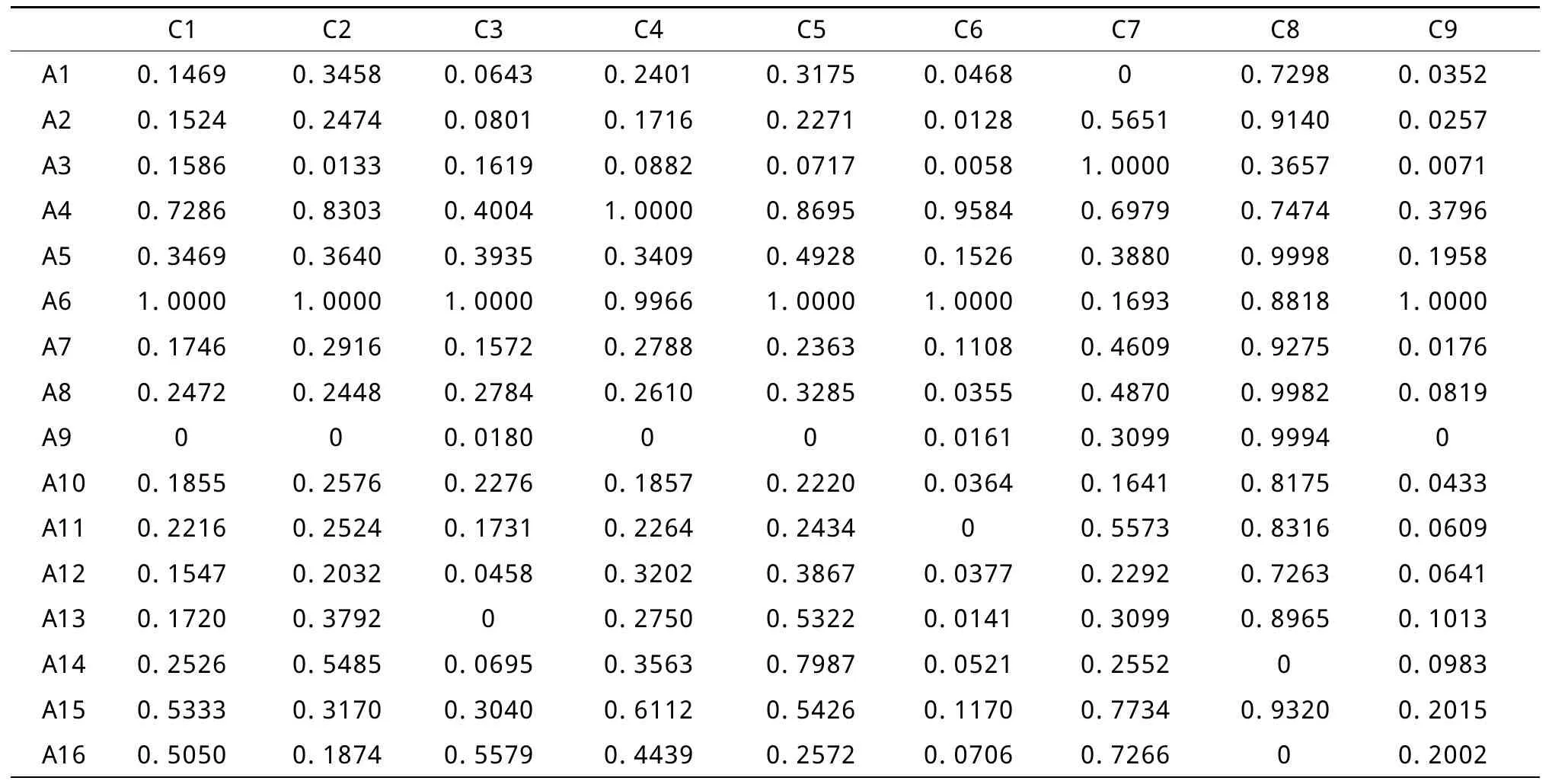
表2 我国16个中心城市各指标的标准化数据

（6）由（12）、（13）、（14）式求得权重向量为：

WT=（0.1141,0.1050,0.1308,0.1005,0.0896,0.1540,0.0799,0.0544,0.1717）

（7）由（15）式求得综合评价值向量为：

ZT=（0.1670,0.1926,0.1578,0.7103,0.3502,0.9269,0.2276,0.2587,0.0839,0.1871,0.2192,0.1864,0.2278,0.2482,0.4090,0.3212）

（8）采用TOPSIS-AHP方法对我国16个中心城市的综合实力进行评价，并将此评价结果与文献[6]改进层次分析法的评价结果进行比较。两种方法对我国16个中心城市的综合评价值及排序结果见表3。

由评价结果可知，两种评价模型的差异体现在深圳、重庆、东莞，如果删去这3个城市，其它13个城市的排序结果不变。为判别哪一个权重更加合理，分别对深圳与杭州、重庆与成都、沈阳与东莞的排名情况进行比较分析。一是深圳在指标C1、C3、C4、C6、C7、C9上的综合评价值均超过了杭州，对TOPSIS-AHP方法来说，这些指标的权重之和为0.751，而对改进层次分析法来说，这些指标的权重之和为0.673，均超过了0.5，所以深圳排在杭州之前是合理的。类似地，对重庆与成都、沈阳与东莞也得到同样的结论。二是分别使用TOPSIS-AHP方法和改进层次分析法确定权重，用线性加权综合评价模型进行评价，我国6个中心城市的综合评价值见表4。从评价结果来看，采用TOPSISAHP方法的评价结果保证了深圳与杭州、重庆与成都、沈阳与东莞的综合评价值的大小与其排名的一致性，而采用改进层次分析法确定权重导致沈阳与东莞的综合评价值大小与其排名互相矛盾。可见，TOPSIS-AHP方法比改进层次分析法确定权重更加切合实际，同时，基于TOPSIS-AHP方法的线性加权综合评价模型在城市综合实力评价中更加合理、更加可靠，更加简单易行。

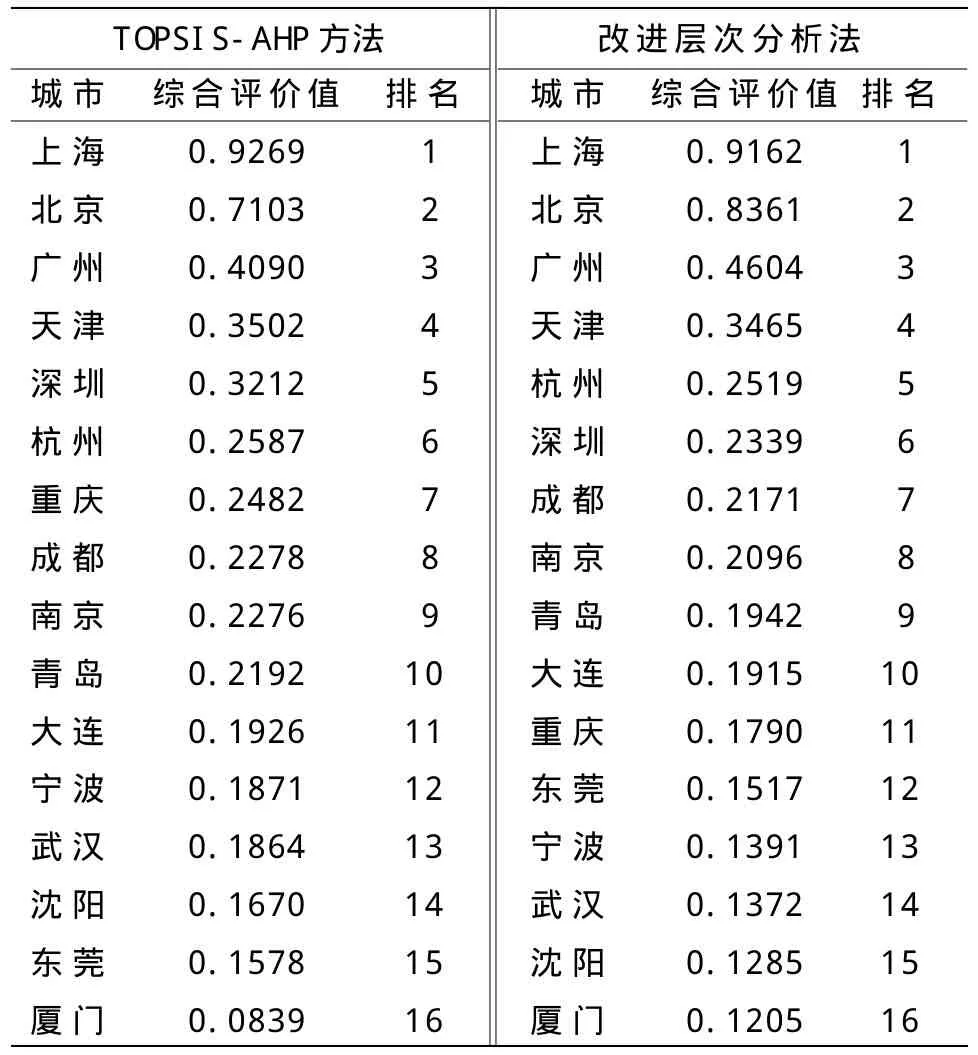
表3 TOPSIS-AHP方法和改进层次分析法对我国16个中心城市的综合评价值及排序

6 结束语

本文将TOPSIS方法与层次分析法的优势结合起来，构建了一种确定多指标权重的方法——TOPSISAHP方法，并将其应用于线性加权综合评价模型中，解决了城市综合实力的评价问题。该方法不仅适用于定量指标，也适用于定性指标；不仅可以解决城市综合实力评价中指标权重的确定问题，而且也为其它多指标多层次的系统评价和决策问题中指标权重的确定提供了一种可行的方法。另外，在城市综合实力评价中，基于TOPSIS-AHP方法确定权重的线性加权综合评价模型，比文献[6]的模糊优选模型更加简单易行，评价结果更加合理可靠。

表4 我国6个中心城市的综合评价值

[1]左军.多目标决策分析[M].杭州:浙江大学出版社，1991:88-90.

[2]徐伟，王波，张伟.AHP法和TOPSIS法在层次性多元分析评价中的综合应用[J].北京化工大学学报:哲学社会科学版，1999，29(2):25-33.

[3]岳超源.决策理论与方法[M].北京:科学出版社，2003:206-208.

[4]冯珍.山西省水利设施发展的因子分析[J].数学的实践与认识，2011，41(13):40-44.

[5]柯铧，柯科.层次分析法在步枪作战效能评估中的应用[J].数学的实践与认识，2011，41(20):155-162.

[6]杨志辉，陈铁牛，刘龙章.基于改进层次分析法的模糊优选模型[J].数学的实践与认识，2010，40(10):25-31.