基于复合材料理论的土壤——根系力学研究

张 飞

(浙江省有色金属地质勘查局，浙江绍兴 312000)

1 引言

生态防护技术是随着世界范围内高速公路建设而兴起的一门工程技术。在越来越重视环境保护和生活质量的今天，生态防护已广泛的应用于公路、铁路边坡以及废弃矿山的环境治理和恢复等众多领域。与传统的工程防护技术不同，生态防护技术充分利用植物自身特点并结合必要的工程防护起到工程建设与环境保护兼顾的目的。目前，关于生态防护技术研究主要集中在对施工工艺的改进以及水土保持学的研究，忽略了坡面植物根系的工程力学行为研究，导致生态防护理论远远落后于防护技术应用的发展，制约生态防护技术在各类工程中的应用。国内外有关学者通过现场试验和数值模拟等方法，对含根系土壤的值进行了相关研究，定量地分析了植物根系的固坡作用［1－5］。

为了开拓生态防护研究的新思路，本文借鉴其他学科理论以研究生态防护的力学效应，将土壤－根系复合体视为一种特殊的复合材料，应用复合材料的细观力学理论，研究分析该“复合材料”中各组分的力学行为、力学效应，用以反映复合体的总体力学行为、力学效应等，并通过计算机模拟试验，对土壤和土壤－根系复合体的力学行为进行研究，为根系对土壤的力学加固效应寻求理论支撑。

2 土壤－根系复合体的细观力学

简单而言，土壤——根系复合体就是混有若干根系的土壤，但该复合体已经不再是单纯的土壤，而是按照一定规律(假设存在规律性)混配、分布的。将土壤——根系复合体视为一种特殊的复合材料时，视土壤为基体，根系为增强相，并假设根系与土壤联结紧密。另外，在本文的研究工作中，只考虑根系与土壤正交的情况，而对它们斜交时的情况不加以考虑。运用细观力学研究分析时，本文还需作如下假设:

(1)土壤－根系根系复合体是宏观均质的、线弹性的、正交异性的，且无初始应力;

(2)增强相(根系)是均质的、线弹性的、各向同性的(或横观各向同性的)、排列规则和取向完善的;

(3)基体(土壤)是均质的、线弹性的、各向同性的;

(4)界面无孔隙、粘结牢固。

3 土壤－根系复合体的细观力学等效模型

根据假设(1)，土壤－根系复合体是正交异性、线弹性、宏观均质的，则其工程常数之间存在如下式所示的关系:

式中，E1、E2、E3是沿弹性主方向 x、y、z 的弹性模量;γ12是x方向伸、缩时决定y方向缩、伸的泊松比，γ21是 y方向伸、缩时决定 x方向缩、伸的泊松比，余类推;G23、G31、G12是决定 y 和 z、z 和 x、x 和 y方向之间夹角变化的剪切模量。

上式可以看作是土壤——根系复合体的正交异性体的弹性力学模型，由马克斯韦尔定理可知弹性模量与泊松比有如下关系:

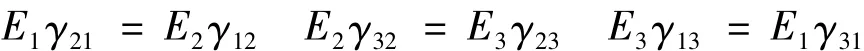
4 确定弹性常数的材料力学方法

4.1 分析模型的建立

在研究分析土壤－根系复合体的弹性常数过程中，虽然将其视为一种复合材料，但同时细观力学也要求将其视为结构，这样就需要建立一种分析模型。分析模型有两项共同的要求:1)组分的体积含量比必须与所代表的材料的相应体积含量比相同;2)模型尺度不妨碍模拟材料的力学响应。本文以我国学者朱颐龄1973年提出的矩形模型法为理论依据建立分析模型。建立土壤——根系复合体矩形分析模型时，将根系的圆形截面视为正方形截面，并取1/4单元(包括1/4根系截面)进行研究，如图1(a)、(b)所示［6－8］。

图1 土壤－根系复合体分析模型

4.2 工程常数的确定

通过各面上的等应力或等应变的假设，根据静力相当条件、变形协调条件及材料的物理关系，可以分别得到土壤——根系复合体与根系、土壤在各轴向上的弹性模量、泊松比、剪切模量关系方程式。

5 虚拟三轴试验

5.1 三轴试验

三轴试验是最普通的用来研究土的应力－应变特性的试验。土样首先承受侧限围压σc，然后增加轴向应力Δσa直至破坏。因为时样周边无剪应力，轴向应力σc+Δσa及侧限应力σc分别为最大σ1、最小主应力σ3。三轴压缩试验的变形主要是体积变形和剪切变形。

5.2 本构关系的选择

在研究岩土材料在某应力状态下的应力、应变时，通常要选用相应的本构模型亦即应力——应变关系。岩土材料的本构关系非常复杂，可分为线弹性、非线弹性、塑性、弹塑性等许多种，一般常用弹塑性与非线弹性本构模型。本文在进行虚拟试验时，采用 Drucker－ Page 模型［9－11］。进行有限元分析时，还需做如下两个假设:

(1)假设根系、土壤分别为各向同性体，而两者所组成的复合体则为各向异性;

(2)假设根系和土壤胶结紧密。

5.3 土壤——根系复合体的虚拟单轴试验

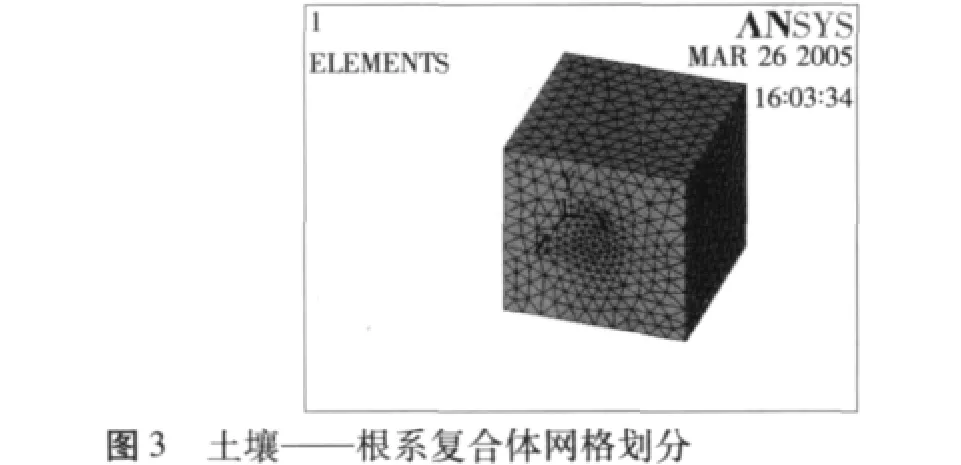
建立尺寸为10mm3的复合体模型，其中根系尺寸为D=1mm，L=10mm，模型建立及网格划分如下图2、图3所示。试验中，分别对y轴和z轴两个方向施加荷载。

5.3.1 z轴方向(根系长度方向)

单轴侧限压缩时，在z=－10mm的面上施加10KPa的z轴方向的轴向应力。定义约束为:z=0平面上所有节点位移为零，即固定z=0平面;各个侧面上的节点只存在z向的位移。试验所得的位移等值图及变形图如图4、图5所示。

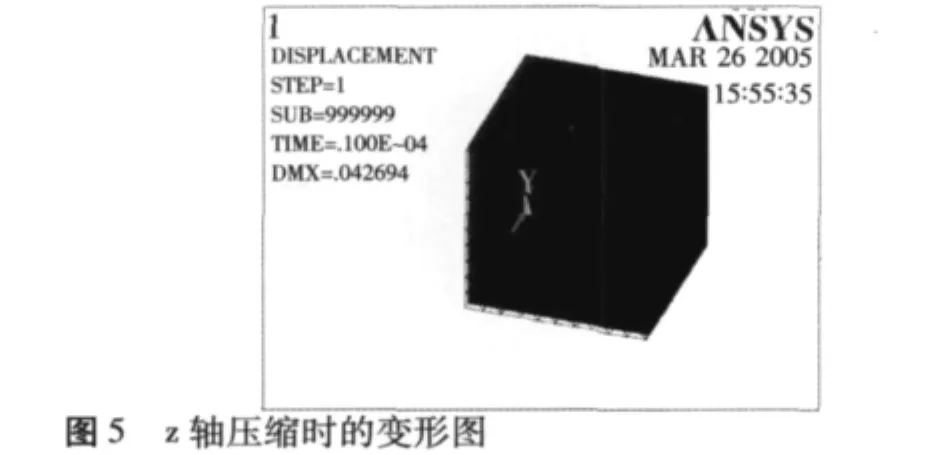
根据试验及位移、变形图可以得知，复合体在z轴方向的应变为εz=－0.0042694。

5.3.2 y轴方向(垂直根系长度方向)

单轴侧限压缩时，在 y=10mm的面上施加10KPa的y轴方向的轴向应力。定义约束为:y=0平面上所有节点位移为零，即固定y=0平面;各个侧面上的节点只存在y向的位移。试验所得的位移等值图及变形图如图6、图7所示。

根据试验及位移、变形图可以得知，复合体在y轴方向的应变为εy=－0.0180706。

6 虚拟试验结果比较

由虚拟试验结果可以看出，土壤——根系复合体在施加z轴方向的轴向应力时，其z轴方向的应变为εz=－0.0042694;施加y轴方向的轴向应力时，其y轴方向的应变为εy=－0.0180706。按照复合材料细观力学理论推导公式，计算得到的试验数据表1。

表1 土壤与根系——土壤复合体的试验结果

由上表明显可知，复合体复合体在z、y轴的应变均小于土壤的应变，尤其是z轴方向上比较明显，而且两种方法计算得到的数据比较接近，这表明了，采用复合材料细观力学理论，对根系－土壤复合体的力学性质、力学行为的研究具有一定的可行性。

7 结论

本文采用复合材料理论的研究方法，通过细观力学等效模型来分析描述根系土的宏观力学性能，以及其细观结构与宏观性能之间的关系。分析表明，复合体的力学性质与各组分(即土壤、根系)力学性质以及各组分的体积分数存在一定关系。一般情况下，复合体的各力学常数与各组分的力学性质或根系的体积分数正相关。

通过有限元模拟根系——土壤复合体的三轴虚拟试验，分析两种土壤在相同应力状态下的不同应变，进一步分析根系的加固作用。试验结果表明，在相同应力状态下，根系——土壤复合体的应变比土壤小。

本文的研究主要是针对于草本植物，全文所作的工作基本上也都是基于这一出发点。同时，出于方便研究，本文做了几种假设，例如将根系在土中的分布简化为与土壤正交并且分布均匀，这些对研究结果产生了一定的误差，但不影响本文研究的初衷，即:将土壤－根系复合体视为一种特殊的复合材料，应用复合材料的细观力学理论，研究分析该“复合材料”中各组分的力学行为、力学效应，用以反映复合体的总体力学行为、力学效应等，并通过计算机模拟试验，对土壤和土壤—根系复合体的力学行为进行研究，为根系对土壤的力学加固效应寻求理论支撑。

［1］ 封金财，王建华.乔木根系固坡作用机理的研究进展［J］.铁道建筑.2004(3):29－31.

［2］ 周跃，徐强，络华松等.乔木侧根对土体的斜向牵引效应－Ⅰ原理和数学模型［J］.山地学报.1999(1):4－9.

［3］ 解明曙.黄土地区林木根系固坡的土力学机制研究［J］.北京:北京林业大学，1988.

［4］ 亚川，莫永京，王芝芳等.土壤－草本植被根系复合体抗水蚀强度与抗剪强度的试验研究［J］.中国农业大学学报.1996(1):31－38.

［5］ 程洪，张新全.草本植物根系网固土原理的力学试验探究［J］.水土保持通报.2002(5):20－23.

［6］ 张开达，杨乃宾.复合材料结构力学［M］.北京:北京航空航天大学出版社，1993.

［7］ 杜善义，王彪.复合材料细观力学［M］.北京:科学出版社，1998.

［8］ 刘锡礼，王秉权.复合材料力学基础［M］.北京:中国建材工业出版社，1998.18－42.

［9］ 朱伯芳.有限单元原理与应用［M］.北京:中国水利水电出版社，1998.

［10］ 孙炳楠，洪滔.工程弹塑性力学［M］.浙江大学出版社，2002.

［11］ 张学言.岩土塑性力学［M］.北京:人民交通出版社，1993.