Existence of a Renorm alised Solu tions for a Class of Non linearDegenerated Parabolic Prob lem sw ith L1Data

AKDIM Y.,BENNOUNA J.,MEKKOURM.,∗and REDWANEH.2Department ofM athematics,Laboratory LAMA,University ofFez,Faculty of

Sciences Dhar ElM ahraz,B.P.1796.Atlas Fez,M orocco.

2Facult´edes Sciences Juridiques,´Econom iques et Sociales,Universit´eHassan 1,

B.P.784.Settat,M orocco.

Existence of a Renorm alised Solu tions for a Class of Non linearDegenerated Parabolic Prob lem sw ith L1Data

AKDIM Y.1,BENNOUNA J.1,MEKKOURM.1,∗and REDWANEH.21Department ofM athematics,Laboratory LAMA,University ofFez,Faculty of

Sciences Dhar ElM ahraz,B.P.1796.Atlas Fez,M orocco.

2Facult´edes Sciences Juridiques,´Econom iques et Sociales,Universit´eHassan 1,

B.P.784.Settat,M orocco.

Received 7August2012;Accep ted 14Decem ber 2012

.We study the existence of renorm alized solu tions for a class of non linear degenerated parabolic p roblem.The Carath´eodory function satisfying the coercivity cond ition,the grow th cond ition and only the largem onotonicity.The data belongs to L1(Q).

Weighted Sobolev spaces;truncations;nonlinear doubling parabolic equation;renorm alized solu tions.

1 In troduction

LetΩbe a bounded open setof RN,p be a realnum ber such that2≤p＜∞,Q=Ω×]0,T[ and w={wi(x),0≤i≤N}bea vectorofw eight functions(i.e.,every com ponent wi(x)isa m easu rable function w hich is positive a.e.inΩ)satisfying som e in tegrability cond itions. The objective of this paper is to study the follow ing p roblem in the w eighted Sobolev space:

The function b is assum ed to be a strictly increasing C1-function,the data f and b(u0)lie in L1(Q)and L1(Ω),respectively.The functionsφis justassum ed to be continuous of R w ith values in RN,and the Carath´eodory function a satisfying on ly the largem onotonicity(see assum p tion(H2)).

Let us poin t ou t,the d ifficu lties that arise in p roblem(1.1)are due to the follow ing facts:the data f and u0only belong to L1,a satisfies the largem onotonicity that is

For the parabolic equation(1.1)the existence of w eak solu tion has been p roved by J.-M.Rakotoson[7]w ith the strictm onotonicity and am easu re data,the existence and uniquenessofa renorm alized solution has been p roved by D.Blanchard and F.M u rat[8] in the casew here a(x,t,s,ξ)is independentof s,φ=0,and by D.Blanchard,F.M u rat and H.Redw ane[9]w ith the largem onotonicity on a.

For the degenerated parabolic equations the existence of w eak solu tions have been p roved by L.Aharouch et al.[10]in the case w here a is strictly m onotone,φ=0 and f∈Lp′(0,T,W-1,p′(Ω,w∗)).See also the existence of renorm alized solu tion by Y.Akd im etal[11]in the casew here a(x,t,s,ξ)is independentof s andφ=0.

Note that,this paper can be seen as a generalization of[9,10]in w eighted case and as a con tinuation of[11].

The p lan of the paper is as follow s.In Section 2w e give som e p relim inaries and the definition ofw eighted Sobolev spaces.In Section 3w em ake p recise all the assum p tions on a,φ,f and u0.In Section 4 w e give som e technical resu lts.In Section 5 w e give the definition of a renorm alized so lu tion of(1.1)and w e establish the existence of such a solution(Theorem 5.1).Section 6 is devoted to an exam p lew hich illustrates ou r abstract resu lt.

2 Prelim inaries

LetΩbe a bounded open setof RN,p be a realnum ber such that1＜p＜∞and w={wi(x), 0≤i≤N}be a vector ofw eight functions,i.e.,every com ponent wi(x)is am easurable function w hich is strictly positive a.e.inΩ.Fu rther,w e suppose in allou r considerations

that,there exists

for any 0≤i≤N.We denote by W1,p(Ω,w)the space of all real-valued functions u∈Lp(Ω,w0)such that the derivatives in the sense of d istribu tions fu lfill

w hich is a Banach space under the norm

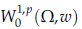
3 Basic assum p tions

Assumption(H1)

For 2≤p＜∞,w e assum e that the exp ression

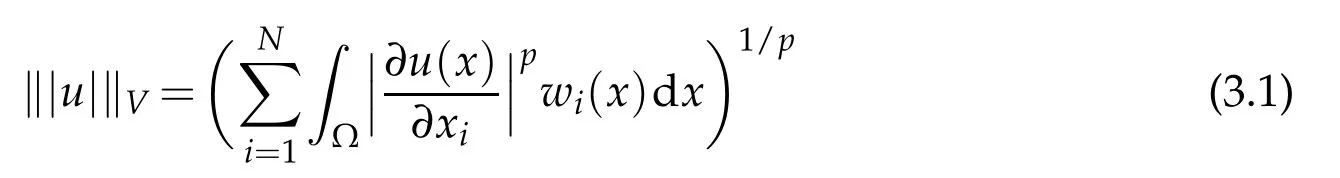
is a norm defined on V w hich equivalent to the norm(2.4),and there exist a w eight functionσonΩsuch that,

We assum e also the Hardy inequality,

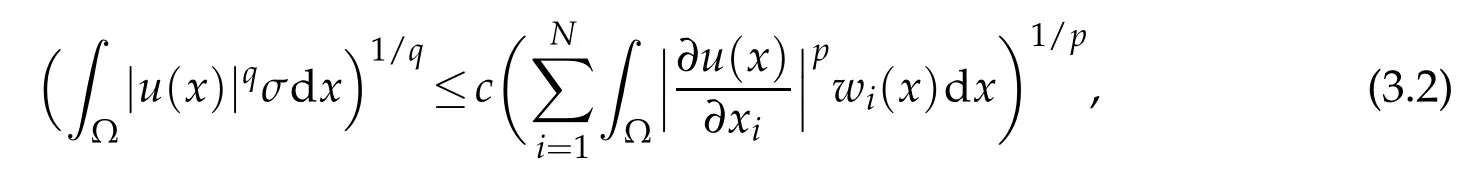
holds for every u∈V w ith a constant c＞0 independen tof u,andm oreover,the im bedd ing

exp ressed by the inequality(3.2)is com pact.Note that(V,‖|·|‖V)is a uniform ly convex (and thus reflexive)Banach space.

Remark3.1.Ifw eassum e that w0(x)≡1and in add ition the integrability cond ition:There

Notice that the assum p tions(2.2)and(3.4)im p ly

Assumption(H2)

We assum e that

b:Ω×R→R isa strictly increasing C1-function w ith b(0)=0,(3.7)

for a.e.(x,t)∈Q,all(s,ξ)∈R×RN,som e function k(x,t)∈Lp′(Q)andβ＞0.Hereσand q are as in(H 1),

W hereαis strictly positive constan t.We recall that,for k＞1 and s in R,the truncation is defined as,

4 Som e technical resu lts

Characterizationofthetimemollificationofafunctionu

In order to deal w ith tim e derivative,w e introduce a tim e m ollification of a function u belonging to a som e w eighted Lebesgue space.Thus w e define for allµ≥0 and all (x,t)∈Q,

Someweightedembeddingandcompactnessresults

In thissectionw eestablish som eem bedd ing and com pactness resu ltsin w eighted Sobolev spaces,som e trace resu lts,Aubin’s and Sim on’s resu lts[14].Let

The dual space of X is X∗=Lp′(0,T,V∗)w here 1/p+1/p′=1 and denoting the space

endow ed w ith the norm

w hich is a Banach space.Here u′stands for the generalized derivative of u,i.e.,

Lemma4.1([15]).1)Theevolution triple V⊆H⊆V is verified.

Lemma4.2([10]).Let g∈Lr(Q,γ)and let gn∈Lr(Q,γ),w ith‖gn‖Lr(Q,γ)≤C,1＜r＜∞.If gn(x)→g(x)a.e.in Q,then gn⇀g in Lr(Q,γ).

Lemma4.3([10]).Assume that,

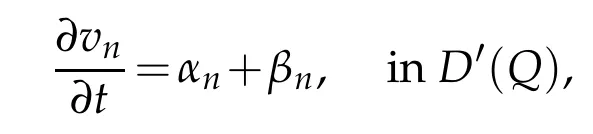
whereαnandβnarebounded respectively in X∗and in L1(Q).If

5 M ain resu lts

Definition5.1.Let f∈L1(Q)and b(u0)∈L1(Ω).A real-valued function u defined onΩ×]0,T[ isa renormalized solution ofproblem(1.1)if

2.掩护部队行动。海上民兵运用海上民船、漂浮物、岛礁、烟雾、复杂气象、海况等作掩护，将民船与部队合编，采取形体掩护、噪音覆盖、民船佯动等方法，掩护小型作战舰艇、潜艇航行，使敌人的侦观通系统难以发现，提高战斗舰艇作战的隐蔽性、突然性、精确性，保障部队对敌实施隐蔽突然的打击。

Remark5.1.Eq.(5.3)is form ally obtained through pointw isem u ltip lication of Eq.(1.1) by S′(u).How ever,w hile a(u,Du)andφ(u)does not in generalm ake sense in(1.1),all the term s in(5.3)have am eaning in D′(Q).

Indeed,if M is such thatsupp S′⊂[-M,M],the follow ing identifications arem ade in (5.3):

•BS(u)belongs to L∞(Q)since S is a bounded function and

•S′(u)a(u,Du)identifiesw ith S′(u)a(TM(u),DTM(u))a.e.in Q.Since|TM(u)|≤M a.e. in Q and S′(u)∈L∞(Q),w e obtain from(3.8)and(5.1)that

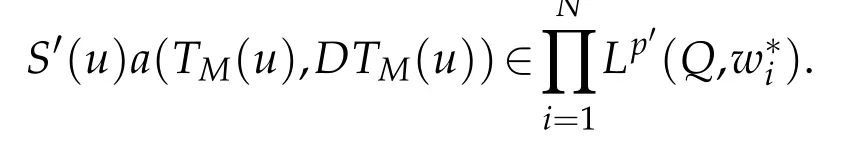
•S′(u)a(u,Du)Du iden tifiesw ith S′′(u)a(TM(u),DTM(u))DTM(u)and

•S′(u)φ(u)Du and S′(u)φ(u)respectively identify w ith

Due to the p ropertiesof S′and to(3.11),the functions S′,S′′andφoTMare bounded on R so that(5.1)im p lies that

and

Theorem5.1.Let f∈L1(Q)and u0∈L1(Ω).Assume that(H 1)and(H 2),there exists at least a renormalized solution u(in the senseofDefinition 5.1).

Proof.Step1:Theapproximateproblem.

For n＞0,letus define the follow ing app roxim ation of b,a,φ,f and u0;

In view of(5.6),ansatisfy(3.10)and(3.8),there exists kn∈Lp′(Q)andβn＞0 such that

φnisa Lipschitz continuousbounded function from R in to RN,(5.8)

such thatφnuniform ly converges toφon any com pact subsetof R as n tends to+∞,

Letus now consider the app roxim ate p roblem:

Step2:The estim ates derived in this step rely on standard techniques for p roblem s of type(5.11).

Using in(5.11)the test function Tk(un)χ(0,τ),w e get,for everyτ∈[0,T].

w hich im p lies that,

Thanks to(3.10)w e have

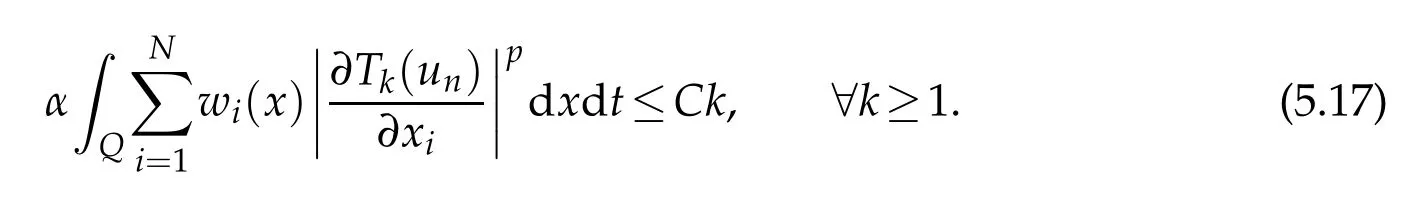
We deduce from thatabove inequality(5.13)and(5.15)that

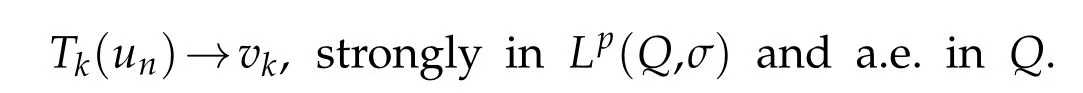
Let k＞0 large enough and BRbe a ballofΩ,w e have,

w hich im p lies that,

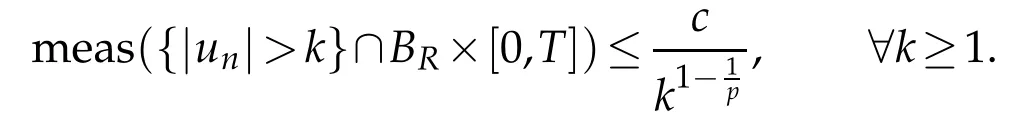
So,w e have

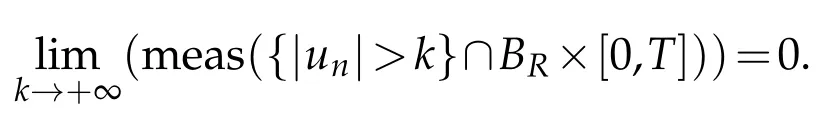
Now w e tu rn to p rove the alm ostevery convergence of unand bn(un).

Consider now a function non decreasing gk∈C2(R)such that gk(s)=s for|s|≤k/2 and gk(s)=k for|s|≥k.

in the sense of d istribu tions,w hich im p lies that

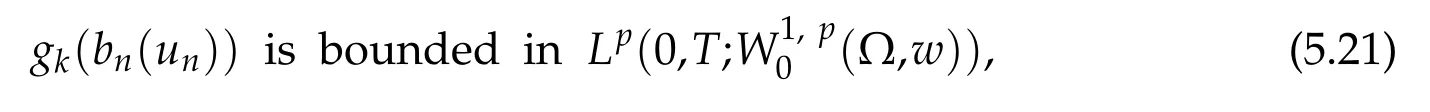
and

independently of n as soon as k＜n.Due to Definition(3.7)and(5.5)of bn,it is clear that

as soon as k＜n and k∗is a constant independentof n.Asa firstconsequencew e have

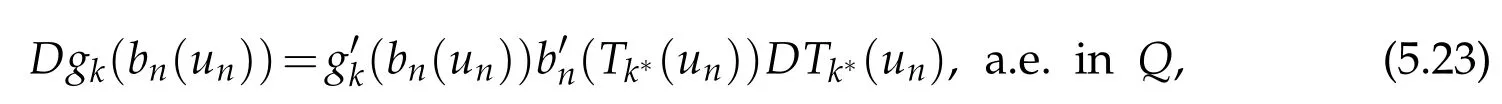
as soon as k＜n.Second ly,the follow ing estim ate holds true

As a consequence of(5.17),(5.23)w e then obtain(5.21).To show that(5.22)holds true, due to(5.20)w e obtain

Thus,for a subsequence,it also converges in m easure and alm ost every w here in Q, due to the choice of gk,w e conclude that for each k,the sequence Tk(bn(un))converges alm osteveryw here in Q(sincew e have,for everyλ＞0,)

Letε＞0,then,there exist k(ε)＞0 such that,

This p roves that(bn(un))is a Cauchy sequence in m easure in BR×[0,T],thus converges alm ost everyw here to som e m easu rable function v.Then for a subsequence denoted again un,

and

w e can deduce from(5.17)that,

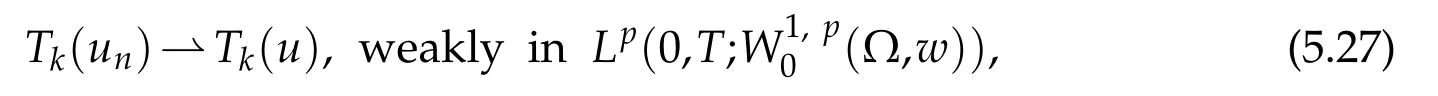
and then,the com pact im bedd ing(3.3)gives,

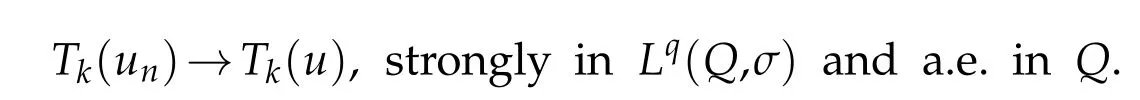
Wenow establish that b(u)belongs to L∞(0,T;L1(Ω)).Using(5.25)and passing to the lim it-in f in(5.18)as n tends to+∞,w e obtain that

Step3:This step is devoted to introduce for k≥0 fixed a tim e regu larization of the function Tk(u)and to establish the follow ing lim its:

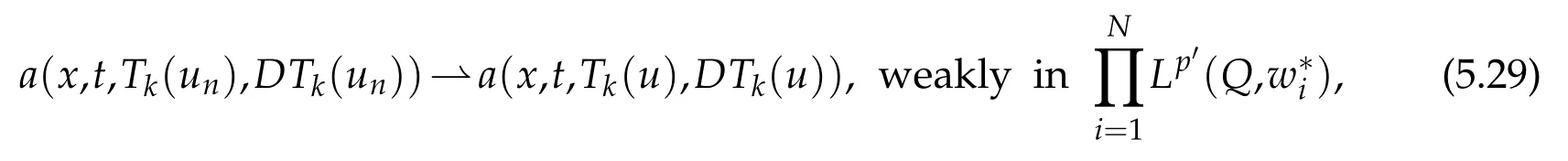
as n tends to+∞.

This p roof is devoted to introduce for k≥0 fixed,a tim e regu larization of the function Tk(u)in order to perform them onotonicitym ethod.

Firstly w e p rove the follow ing lemm a:

Lemma5.1.

forany integerm≥1.

Proof.Taking T1(un-Tm(un))as a test function in(5.11),w e obtain

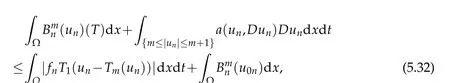
Finally by(3.13),(3.12)and(5.33)w e get

The p roof is com p lete.

The very definition of the sequence(Tk(u))µforµ＞0(and fixed k)w e establish the follow ing lemm a.

Lemma5.2.Let k≥0 be fixed.Let(Tk(u))µthemollification ofTk(u).Let S be an increasing C∞(R)-function such that S(r)=r for|r|≤k and supp S′is compact.Then,

We p rove the follow ing lemm a,w hich is the key pointin them onotonicity argum ents.Lemma5.3.Thesubsequenceofunsatisfies forany k≥0

wherehkisdefined in(5.28).

Proof.In the follow ing w e adap t the above-m en tioned m ethod to p roblem(1.1)and w e first introduce a sequenceof increasing C∞(R)-functions Smsuch that

w e obtain upon integration over(0,t)and then over(0,T):

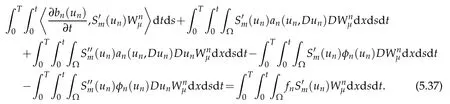
In the follow ing w e pass the lim it in(5.37)asn tends to+∞,thenµtends to+∞and then m tends to+∞,the realnum ber k≥0 being kep t fixed.In order to perform this task w e p rove below the follow ing resu lts for fixed k≥0:

w e deduce that for fixedµ＞0

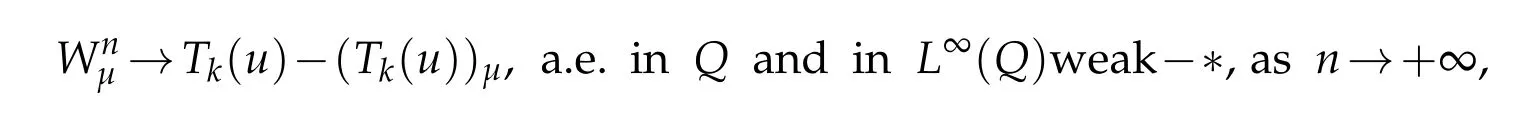
as n tends to+∞.Asa consequenceof(5.46)and(5.44),w e deduce that

for anyµ＞0.

Passing to the lim it asµ→+∞in(5.45)w e conclude that(5.39)holds true.

Proofof(5.40).For fixed m≥1,and by the sam e argum en ts that those that lead to (5.46),w e have

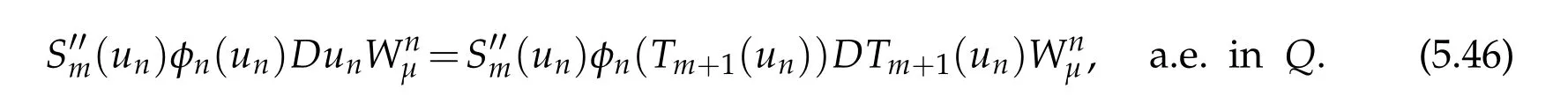
From(3.11),un→u a.e.in Q and(5.27),it follow s that for anyµ＞0

for anyµ＞0.

Passing to the lim itasµ→+∞in(5.45)w e conclude that(5.40)holds true.

for any m≥1,anyµ＞0 and any n≥1,it is possible to obtain

for any m≥1,w here C isa constan t independen tof m.Appealing now to(5.30)itpossible to pass the lim itasm tends to+∞to establish(5.41).

Proofof(5.42).Lebesgue’s convergence theorem im p lies that for anyµ＞0 and any m≥1

Now,for fixed m≥1,using Lemm a 4.1 and passing to the lim it asµ→+∞in the above equality to obtain(5.42).

Wenow turn back to the p roofof Lemm a5.3.Due to(5.38)-(5.42),w eare in a position to pass the lim it-sup w hen n tends to+∞,then to the lim it-sup w henµtends+∞and then to the lim itasm tends to+∞in(5.37).We obtain by using the definition of Wnµthat for any k≥0

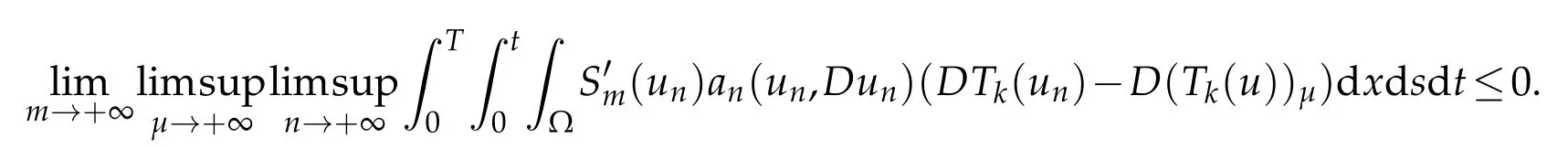
The right-hand side of(5.48)is com pu ted as follow s.We have for n≥m+1:

Due to thew eak convergence of a(DTm+1(un))it follow s that for fixed m≥1

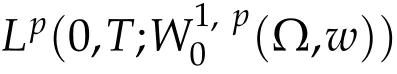
w hich im p lies that,passing to the lim itas n→+∞,

Asa consequence of(5.50)w e have for k≤m,

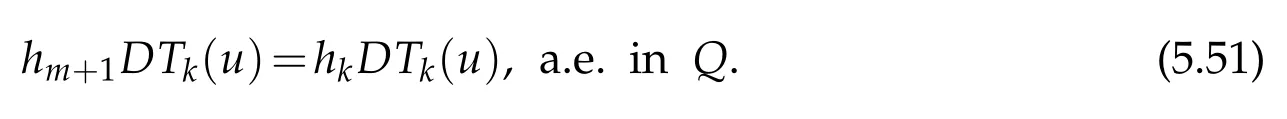
Recalling(5.48),(5.49),(5.51)w e conclude that(5.36)holds true and the p roofof Lemm a 5.3 is com p lete.

In this lemm aw e p rove the follow ingm onotonicity estim ate:

Lemma5.4.Thesubsequenceofu satisfiesforany k≥0

Proof.Let k≥0 be fixed.The character(3.9)of a(x,t,s,d)w ith respect to d im p lies that

To pass to the lim it-sup as n tends to+∞in(5.53)im p ly that

and that,

uniform ly w ith respect to n.

It follow s thatw hen n tends to+∞

Lemm a 5.3,w eak convergence of DTk(un),a(Tk(un),DTk(un))and(5.54)m ake it possible to pass to the lim it-sup as n→+∞in(5.53)and to obtain the resu lt.

In this lemm a w e identify thew eak lim it hkand w e p rove thew eak-L1convergence of the“truncated”energy a(T(un),DTk(un))DT(un)as n tends to+∞.

Lemma5.5.Forfixed k≥0,wehave

Proof.The p roof is standard oncew e rem ark that for any k≥0,any n＞k and any d∈RN

w hich togetherw ith w eak convergenceof(Tk(un)),a(DTk(un))and(5.54)w eobtain from (5.52)

TheusualM inty’sargum en tapp lies in view ofw eak convergenceof(Tk(un)),a(DTk(un)) and(5.57).It follow s that(5.55)hold true.

In order to p rove(5.56),w e observe thatm onotone character of a and(5.52)give that for any k≥0 and any T′＜T

M oreover,w eak convergence of(Tk(un))and a(DTk(un)),(5.58),(5.54)and(5.55)imp ly that

and

Using the above convergence resu lts in(5.58)show s that for any k≥0 and any T′＜T

as n→+∞.

A t the possible expense of extend ing the functions a(x,t,s,d),f on a tim e interval (0,¯T)w ith¯T＞T in such a w ay that assum p tionsw ith a and f hold truew ith¯T in p lace of T,w e can show that the convergence resu lt(5.59)is stillvalid in L1(Q)-w eak,nam ely that(5.56)holds true.

Step4:In this step w e p rove that u satisfies(5.2).

Lemma5.6.The lim itu oftheapproximate solution unof(5.11)satisfies

Proof.To this end,observe that for any fixed m≥0,one has

Accord ing to(5.56),one isat liberty to pass to the lim itas n→+∞for fixed m≥0 and to obtain

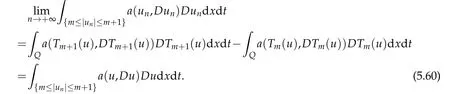
Taking the lim it as m→+∞in(5.60)and using the estim ate(5.30)show that u satisfies (5.2)and the p roofof the lemm a is com p lete.

Step5:In thisstep,u isshow n to satisfy(5.3)and(5.4).Let S bea function in W1,∞(R) such that S hasa com pact support.Let M be a positive realnum ber such that supp(S′)⊂[-M,M].Poin tw isem u ltip lication of the app roxim ate equation(5.11)by S′(un)leads to

Itw as follow sw e pass to the lim it as in(5.61)n tends to+∞.

•Lim itof-d iv[S′(un)an(un,Dun)].

Since supp(S′)⊂[-M,M],w e have for n≥M

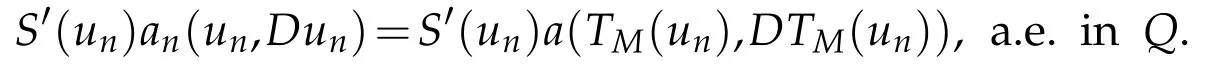
The pointw ise convergence of unto u and(5.55)as n tends to+∞and the bounded character of S′perm itus to conclude that

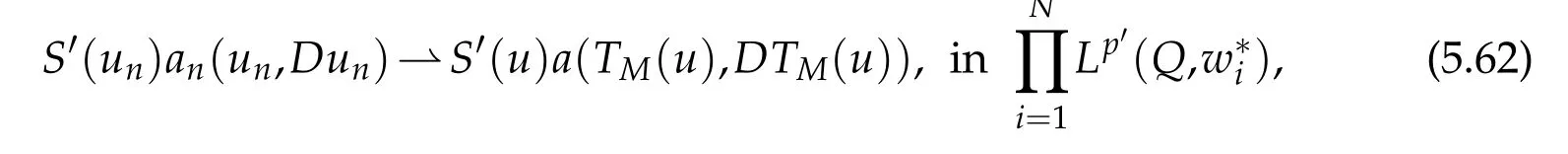
as n tends to+∞.S′(u)a(TM(u),DTM(u))has been denoted by S′(u)a(u,Du)in(5.3).

•Lim itof S′(un)a(un,Dun)Dun.

As far as the’energy’term

Thepointw ise convergenceof S′(un)to S′(u)and(5.56)as n tends to+∞and thebounded character of S′perm itus to conclude that

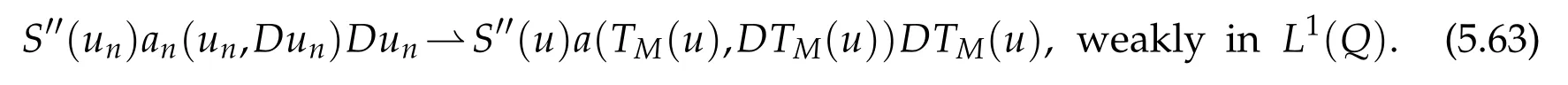
Recall that

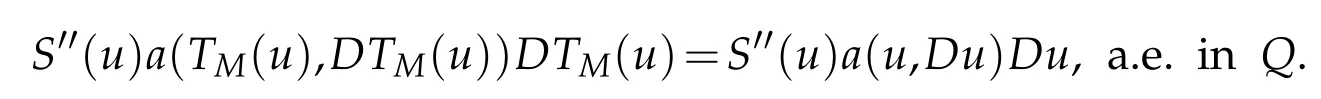
•Lim itof S′(un)φn(un).

Since supp(S′)⊂[-M,M],w e have

Asa consequence of(5.8)and un→u,a.e.in Q,it follow s that

as n tends to+∞.The term S′(u)φ(TM(u))is denoted by S′(u)φ(u).

•Lim itof S′(un)φn(un)Dun.

Since S′∈W1,∞(R)w ith supp(S′)⊂[-M,M],w e have

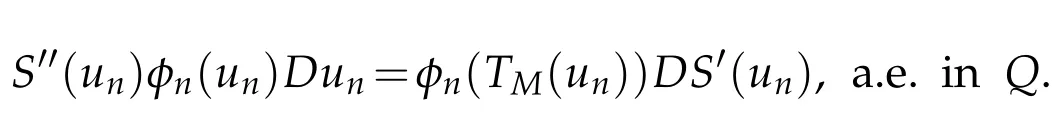
M oreover,DS′(un)converges to DS′(u)w eak ly in Lp(Q,w)as n tends to+∞,w hile φn(TM(un))is uniform ly bounded w ith respect to n and convergesa.e.in Q toφ(TM(u)) as n tends to+∞.Therefore

The termφ(TM(u))DS′(u)=S′′(un)φ(u)Du.

•Lim itof S′(un)fn.

Due to(5.9)and un→u a.e.in Q,w e have Asa consequenceof theabove convergence resu lt,w eare in a position to pass to the lim it as n tends to+∞in Eq.(5.61)and to conclude that u satisfies(5.3).

Asa conclusion of step 1 to step 5,the p roofof Theorem 5.1 is com p lete.

6 Exam p le

Letus consider the follow ing special case:

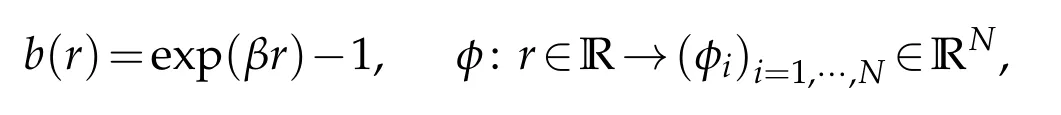
w here

φisa continuous function.And,

w ith wi(x)aw eight function(i=1,···,N).For sim p licity,w e suppose that

It is easy to show that the ai(t,x,d)are Caratheodory functions satisfying the grow th cond ition(3.8)and the coercivity(3.10).On theorder hand them onotonicity cond ition is verified.In fact,

In particu lar,let us use specialw eight function,w,exp ressed in term sof the d istance to the bounded∂Ω.Denote d(x)=d ist(x,∂Ω)and set w(x)=dλ(x),such that

Remark6.1.The cond ition(6.1)is su fficien t for(3.4).

Finally,the hypotheses of Theorem 5.1 are satisfied.Therefore,for all f∈L1(Q),the follow ing p roblem:

has at leastone renorm alised solu tion.

Remark6.2.For uniquenessofa renorm alized solu tion of(1.1)w eare currently w orking w ith doubling variable technique.

Acknow ledgm en ts

The au thorsw ou ld like to thank the anonym ous referees for their usefu lsuggestions.

[1]Dall’aglio A.and Orsina L.,Non linear parabolic equationsw ith natu ral grow th cond itions and L1data.Nonlinear Anal.,27(1996),59-73.

[2]Landes R.,On the existence of w eak solutions for quasilinear parabolic initial-boundary value p roblem s.Proc.Roy.Soc.Edinburgh Sect.A,89(1981),321-366.

[3]Diperna R.J.and Lions P.L.,On the cauchy p roblem for Boltzm an equations:global existence and w eak stability.Ann.ofM ath.,130(2)(1989),321-366.

[4]Boccardo L.,GiachettiD.,Diaz J.-I.,M u rat F.,Existence and regu larity of renorm alized solu tions of som e ellip tic p roblem s involving derivatives of non linear term s.J.Differential Equations,106(1993),215-237.

[5]Rakotoson J.M.,Uniqueness of renorm alized solutions in a T-set for L1data p roblem s and the link betw een various form u lations.Indiana University M ath.J.,43(2)(1994),285-293.

[6]M aso G.Dal,M u rat F.,Orsina L.and Prignet A.,Definition and existence of renorm alized solu tions of ellip tic equationsw ith generalm easu re data.C.R.Acad.Sci.Paris,325(1997), 481-486.

[7]Rakotoson J.M.,T-sets and relaxed solutions for parabolic equations.Journal ofDifferential EquationsBelgium,111(1994),Ju ly 15.

[8]Blanchard D.and M u rat F.,Renorm alized solu tions of non linear parabolic p roblem s w ith L1data:existence and uniqueness.ProceedingsoftheRoyal Society ofEdinburgh,127A(1997), 1137-1152.

[9]Blanchard D.,M urat F.and Redw ane H.,Existenceand uniquenessof renorm alized solution for a fairly generalclassofnonlinear parabolic p roblem s.J.DifferentialEquations,177(2001), 331-374.

[10]Aharouch L.,Azrou l E.and Rhoudaf M.,Strongly non linear variationalparabolic p roblem s in w eighted sobolev spaces.The Australian journalofM athematical Analysisand Applications, 5(2)(2008),1-25.

[11]Akd im Y.,Bennouna J.,M ekkour M.and RhoudafM.,Renorm alised solutions of nonlinear degenerated parabolic p roblem s w ith L1data:existence and uniqueness,recent developm ents in non linear analysis-Proceed ingsof the Con ference in M athem atics and M athem aticalPhysicsWorld Scientific Publishing Co.Pte.Ltd.http:ww w.w orldscibooks.comm athem a tics/7641.htm l.

[12]Ku fner A.,Weighted Sobolev Spaces.John W iley and Sons,1985.

[13]Drabek P.,Ku fner A.and N icolosi F.,Non Linear Ellip tic Equations,Singu lar and Degenerated Cases.University ofWest Bohem ia,1996.

[14]Sim on J.,Com pact sets in the space Lp(0,T,B).Ann.M at.Pura.Appl.,146(1987),65-96.

[15]Zeid ler E.,Nonlinear Functional Analysisand its App lications.Sp ringer-Verlag,New York-Heid lberg,1990.

[16]Lions J.L.,Quelques M´ethodes De R´esolution Des Probl`em e Aux Lim ites Non Lineaires. Dundo,Paris,1969.

[17]Redw ane H.,Solu tion Renorm alis`ees De Probl`em es Paraboliques Et Ellep tique Non lin´eaires.Ph.D.thesis,Rouen,1997.

[18]H icham Redw ane,Existence of a solu tion for a class of parabolic equations w ith three unbounded nonlinearities.Adv.Dyn.Syst.Appl.,2(2007),241-264.

[19]Adam s R.,Sobolev Spaces,AC,Press,New York,1975.

[20]Aharouch L.,Azrou l E.and Rhoudaf M.,Existence resu lt for variational degenerated parabolic p roblem s via pseudo-m onotonicity.Procced ing of the 2005 ou jda International con ference.Elec.J.Diffe.Equ.,2006,9-20.

[21]Akd im Y.,Bennouna J.,M ekkour M.,Renorm alised solutions of nonlinear degenerated parabolic equationsw ith naturalgrow th term s and L1data.International J.Evolution equations,5(4)(2011),421-446.

[22]Blanchard D.,Truncations and m onotonocity m ethods for parabolic equations.Nonlinear Anal.,21(1993),725-43.

[23]Berkovits J.and M ustonen V.,Topologicaldegree for perturbationsof linearm axim alm onotonem appings and app lications to a class of parabolic p roblem.Rendiconti diM atematica, Serie VII,12(1992),597-621.

[24]D rabek P.,Ku fner A.and M ustonen V.,Pseudo-m onotonicity and degenerated or singu lar ellip tic operators.Bull.Austral.M ath.Soc.,58(1998),213-221.

10.4208/jpde.v26.n1.6 March 2013

∗Correspond ing author.Email addresses:akdimyoussef@yahoo.f r(Y.Akd im),jbennouna@hotmai l.com(J. Bennouna),mekkour.mouni r@yahoo.f r(M.M ekkour),redwane hicham@yahoo.f r(H.Redw ane)

AMSSubjectClassifications:A 7A 15,A 6A 32,47D 20

ChineseLibraryClassifications:O175.27