Delaunay 三角剖分在水轮机特性曲线处理中的应用❋
2013-05-04雷恒,张兵
雷 恒,张 兵
(1.黄河水利职业技术学院 水利系,河南 开封 475003;2.小流域水利河南省高校工程技术研究中心,河南 开封 475003)
0 引言
在应用计算机辅助设计技术进行水轮机的选型设计、经济运行和过渡过程数字仿真等工作时,常采用大量离散数据点表示水轮机特性曲线。而水轮机特性曲线数据是由转轮模型试验获得的,这些特性曲线均是一系列大量的离散数据点,即以单位流量Q11和单位转速n11作为坐标系的一系列等值平面曲线数据点[1]。实质上是用二维的图形表述三维的信息,表达不直观。本文针对不规则离散的水轮机特性数据,利用MATLAB强大的数据处理功能[2],通过三次样条插值和Delaunay三角剖分求取水轮机特性曲线。
1 水轮机特性离散数据采集
水轮机流量特性为Q11=f(α,n11)(α为水轮机导叶开度),实际上是水轮机模型综合特性在三维坐标系(Q11,n11,α)中的三维曲面投影到(n11,Q11)平面上的一系列等高线。在MATLAB程序中,首先要为X、Y、Z三个变量进行赋值,再把在Excel表格中处理好的数据列复制、粘贴到MATLAB的变量值表中,这样能够把大量的列项量数值快速地复制给MATLAB中的变量。为了表示各采样点的地理位置,需要绘制采样点的分布图,如图1所示。
2 数据插值和等值线的绘制[3]
水轮机特性采样点多,呈不规则分布,其生成的等值线或等值面(如图2所示)需要进行数据插值和数据网格化。常用的插值算法有线性插值、最近邻插值、三次多项式插值和样条插值4种。其中线性插值和最近邻插值结果所构成的曲面不平滑,精度较低;三次多项式插值结果所构成的曲面较平滑;样条插值结果所构成的曲面最平滑,精度高。
在任意插值计算区间[a,b]的每一个子区间[xk,xk+1]上,三次样条函数为:
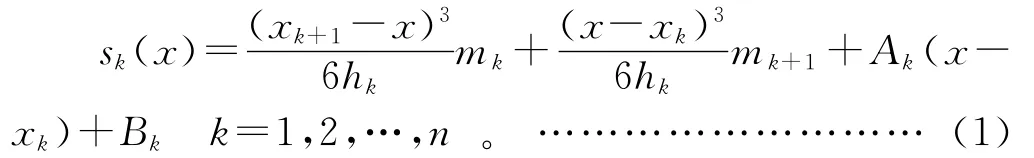
其中:x为水轮机的单位转速;hk为相邻水轮机单位转速的差值,记为hk=xk+1-xk;mk为三次样条插值函数的二阶导数;Ak、Bk为积分常数sk(xk+1)。y为水轮机的单位流量;mk可通过下面方程组解出:

三次样条插值的计算步骤如下:首先确定端点条件,然后构成相应的方程式组(2),求出mk(k=1,2,3,…,n),最后根据式(1)求得各子区间[xk,xk+1]上的三次样条插值函数。

图1 水轮机流量特性曲线离散数据样本分布

图2 等值线图
3 插值三维网格曲面绘制和Delaunay三角网
通过MATLAB可以实现三维网格曲面图形的绘制[4]。插值数据生成的三维网格见图3,生成的三维表面图见图4。

图3 插值数据形成的三维网格图
不规则三角网可减少规则格网方法带来的数据冗余,同时计算效率也较高。如何把一个散点集合剖分成不均匀的三角形网格,这就是散点集的三角剖分问题。不规则三角网模型是根据区域有限个点集将区域划分为相连的三角面网格,区域中任意点落在三角面的顶点、边上或三角形内。在实际中,运用最多的三角剖分是Delaunay三角剖分[5]。
要满足Delaunay三角剖分必须符合两个重要的准则:一是最大-最小化角特性,即在散点集可能形成的三角剖分中,Delaunay三角剖分所形成的三角形最小角最大;二是空圆特性,即Delaunay三角网是唯一的(任意4点不能共圆),在Delaunay三角网中,任一三角形的外接圆范围内不会有其他点存在。

图4 插值数据形成的三维表面图
生成的三维三角网格图见图5,生成的三维三角网曲面图见图6。
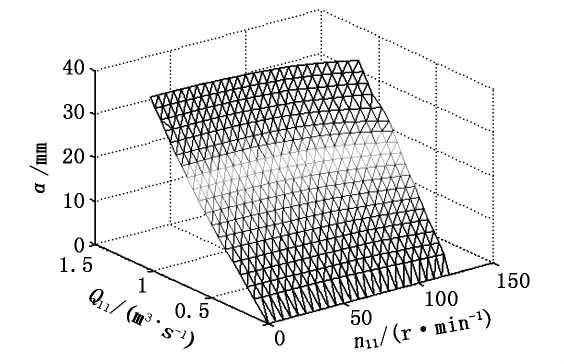
图5 三维三角网格图

图6 三维三角网曲面图
4 结果比较分析
通过计算,对三维曲面中的开度值α与原图的等开度值α作比较,处理结果见图7。
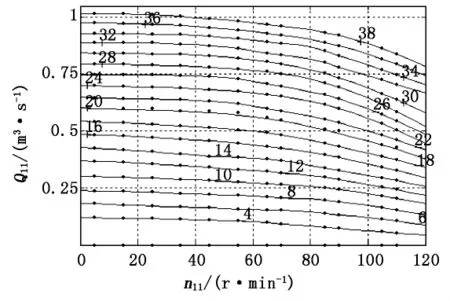
图7 处理结果比较
在图7中取误差最大的一条等开度线(α=20 mm)作误差分析,其数据见表1。通过比较可知,最大绝对误差不超过0.2 mm。由此可见,本文提出的求取水轮机特性曲线中随机插值点的方法是可行的,能满足工程的实际要求。

表1 水轮机特征值计算结果及与原值对比(α=20 mm)
5 结论
本文针对不规则离散的水轮机特性,利用MATLAB强大的数据处理功能,通过三次样条插值和Delaunay三角剖分确保了其计算精度和唯一性,对水轮机的正确选型和优化设计是有利的。
[1] 张昌期.水轮机-原理与数学模型[M].武汉:华中工学院出版社,1988.
[2] 蔡旭辉,刘卫国,蔡立燕.MATLAB基础与应用教程[M].北京:人民邮电出版社,2009.
[3] 张蓉生,刘志鹏,屈波.水轮机模型特性图计算机辅助数据采集及拟合与运转特性曲线的生成[J].机械工程学报,2006(4):222-226.
[4] 王宣怀,沈祖诒,孙涌.基于主曲线方法的水轮机特性曲线的数值拟合[J].水力发电学报,2009,28(3):181-186.
[5] 刘岩,关振群,张洪武,等.面向大规模科学计算的三维Delaunay快速插点算法[J].中国科学:物理学 力学 天文学,2012(2):192-198.
