地层参数对套管外挤应力的影响及屈曲分析

2013-05-04文良凡胡定智邓静静滕立强杨明明

石油矿场机械 2013年4期

文良凡，胡定智，王磊，邓静静，滕立强，杨明明

（1.中国石油技术开发公司钻探装备部，北京100026；2.吐哈油田井下技术作业公司塔里木分公司，新疆库尔勒841600；3.西部钻探钻井工程技术研究院，新疆鄯善838202；4.大庆油田公司第七采油厂，黑龙江大庆163517；5.中国石油长城钻探工程公司苏里格气田项目部，辽宁盘锦124000） ①

套管损坏的主要原因有油层出砂、腐蚀、非均质地应力以及热应力等。套管入井后，随着井眼周围原始地应力场的逐渐恢复，非均质地应力对套管的影响逐渐增大。已有一些文献利用截面静力法［1］、本构方程［2］以及有限元法［3］研究了非均匀载荷作用下套管屈服时的等效应力。也有学者将非均质原场地应力分解为平均应力分量和偏差分量［4］，推导了套管外挤力的数学表达式。本文借助均质地应力作用下挤压应力解，建立了应力椭圆分布模型。通过分析地层的弹性模量、泊松比和原场非均匀地应力这3个参数，采用ANSYS有限元软件模拟套管屈曲变形，更直观地反映了套管在挤压应力作用下的变形规律。

1 原场均匀地应力作用下套管外挤应力

存在于地壳中的应力称为地应力，其值随空间位置不同而变化。存在于当前地壳内的应力场叫做现代应力场。我国大多数油田在开发过程中都遇到了由于原始不均匀地应力场形成的套管径向不均匀载荷，造成油水井套管大量挤毁。

依据弹性力学理论，有

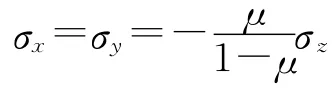
式中：μ为岩石的泊松比，它的取值一般在0.15～0.30［4］；σx和σy为水平应力分量；σz为垂直应力分量。

由于地球介质在应力长时间作用下会产生流变，使水平与垂直应力分量之间的差异逐渐消失，所以一般认为重力引起的是一个各向均等的静岩应力状态，即

式中：γ为岩石容重；z为埋深，负号表示压应力。

如果原场地应力分布均匀，即，σh＝σH＝σ，将地层近似为半径无穷大的圆。假设地层和套管符合厚壁圆筒载荷模型，如图1。由平面应变问题几何方程以及本构方程可以得到厚壁圆筒的位移关系式［5］，即

式中：q1为圆筒内压；q2为圆筒外压；E为弹性模量；a为圆筒内半径；b为圆筒外半径；μ为泊松比。

目前，我国旅游行业发展的过程中，旅游管理将主要的精力放在旅游业务上，忽视对景区生态环境的管理，生态环境破坏比较严重，旅游业的创收是以牺牲环境为代价的，不利于旅游企业的长远发展，同时还会加大环境治理的难度，后期需要投入的环境治理成本比较多，这样就会直接影响到旅游经济效益。另外，缺乏建设旅游基础设施的意识，相关的配套设施不是很齐全，比如污水排放设施、清洁设施等，人们在旅游中不能获取良好的服务体验。

将套管与地层作为整体建模，仅受地应力作用，如图2。将厚壁圆筒的径向位移方程分别用于地层和套管，利用地层区域内边界和套管外边界位移连续条件可以得到套管外壁的挤压应力s1与地应力σ的关系式，即式中：a0为套管内半径；a1为套管外半径；下角标s代表地层；下角标c代表套管。

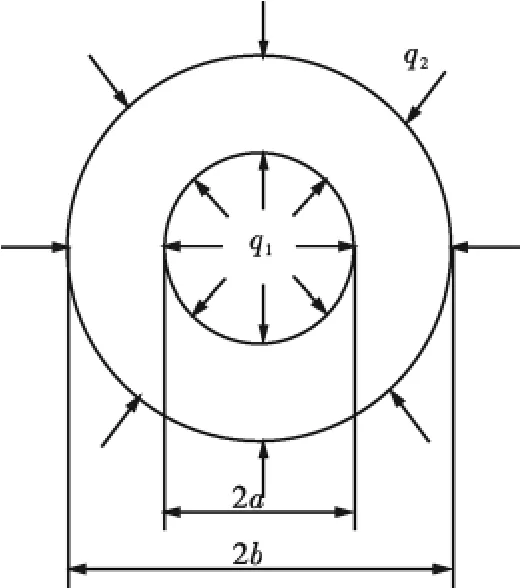
图1 承受内、外压力的厚壁筒示意

图2 地层－套管体系原场地应力示意

2 地层参数对套管外挤应力的影响

套管和地层物性参数如表1所示。

表1 套管和地层物性参数

保持套管参数不变，分别对不同的地层弹性模量和泊松比进行了计算，结果如图3。

其中，套管外壁挤压应力系数＝套管外壁挤压应力/均布原场地应力

由图3可以看出：随着地层弹性模量的减小，套管外挤力系数值逐渐增大；在弹性模量为定值的条件下，泊松比越大，外挤应力系数越低。因此，地层的弹性模量、泊松比越小，地层原场应力对套管外挤应力的影响越明显，外挤应力取值为（0.87～1.31）σ，σ为均布原场地应力。由于地层泊松比变化范围较小，对外挤力系数影响不大，所以地层的弹性模量和泊松比这2个参数中，弹性模量的大小直接关系到套管外挤应力系数的大小。

图3 地层参数与套管外挤应力曲线

3 原场非均质地应力作用下套管外挤应力

当σh≠σH时，在地层原场地应力作用下，套管外壁应力s（θ＝0°）≠s（θ＝90°）。为了使套管外壁外挤应力随θ变化均匀，假设θ＝0°对应于应力椭圆长轴，θ＝90°对应于应力椭圆短轴。套管外壁外挤应力符合椭圆分布规律，如图4。

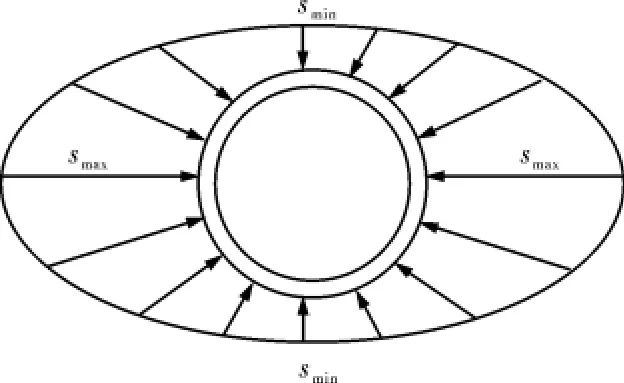
图4 套管外壁挤压应力椭圆分布

将坐标轴换成极坐标形式，即x＝rcosθ，y＝rsinθ得到

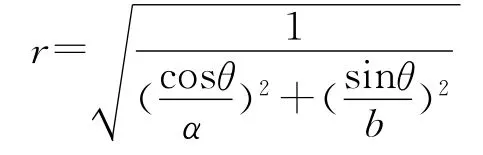
令最大a＝smax＝s2，b＝smin＝s3，则套管外壁应力随角度变化的表达式为

4 非均质地应力下套管屈曲强度分析

在进行实例分析前，首先引入外挤应力非均质率ε，椭圆比率为e＝b/a＝s2/s3，椭圆比率e＝ε。

对于套管来说，当应力低于比例极限时，应力－应变曲线是线性的；而超过屈服点后，材料表现为塑性，应力－应变曲线出现非线性的关系，直至破坏。在塑性分析中，一般遵循屈服准则、流动准则、强化准则［6］。其中，屈服准则是一个可以用来与单轴测试屈服应力相比较的应力状态的标量表示。如果弄清楚应力状态和屈服准则，ANSYS程序就能确定材料是否有塑性变形产生。一个通用的屈服准则是Von Mises，当等效应力超过材料的屈服应力时，将会发生塑性变形。

套管材料的应力－应变呈现非线性分布，当材料从初始点加载到540 MPa时，材料处于弹性阶段，应力、应变2个参数基本呈现线性关系，载荷继续增加时，材料开始发生屈服，应力增加缓慢，应变增长速率加快。

分析过程中，可以将套管的强度与变形问题简化成平面问题。取套管横向截面分析即可，将实体模型转化为平面模型可以大幅降低计算机处理的时间，从而可以加大网格的精密程度，使得结果更加精确。本文选取的有限元单元类型为plane82，八节点平面单元，该单元具有很好地分析材料塑性、大变形的特性。

4.1 非均质率ε＝1.5时套管的应力和变形

选取规格为177.8 mm×10.36 mm的N80套管进行有限元分析，载荷施加函数为

载荷分布如图5。通过采用载荷步逐步加载的方法，直至套管发生屈曲变形，如图6。

图5 非均质率为1.5时套管的载荷分布

图6 非均质率为1.5时套管屈曲变形示意

套管左端点应力－位移关系曲线如图7，可以看出：当套管左端点（x＝－177.8/2，y＝0）载荷从3 MPa加载到18.5 MPa时，该点位移基本在0～1.8 mm区间呈线性增长，然后位移迅速产生畸变，发生屈曲变形。因此，在均匀载荷下，ANSYS模拟的套管外壁承受的最大围压为18.5 MPa。

图7 套管左端点应力－位移关系曲线

4.2 屈曲前均质与非均质挤压应力下套管的等效应力

加载时采取载荷步逐步加载的方式，调用套管产生屈曲变形前一载荷步，分别得到同一套管在均匀载荷下的Mises等效应力云图（如图8）和非均匀载荷作用下对应的Mises等效应力云图（如图9）。从图中可以看出：

1）在均匀地应力作用下，套管内Mises等效应力分布由外壁向内壁逐渐增大，而且分布均匀，随着外挤应力的逐渐增大，套管首先从内壁开始屈服。

2）在非均质地应力作用下，套管内的Mises应力分布发生了较大的变化，产生了不规则局部应力集中云图，位于套管内壁上下以及外壁左右4处等效应力值较大，首先进入屈服状态，表现为套管沿着x轴被挤扁。

图8 均质地应力下套管的Mises应力云图

图9 非均质地应力下套管的Mises应力云图

4.3 ANSYS计算的套管抗挤强度与API标准对比

为了验证软件分析结果的合理性，对不同壁厚的177.8 mm N80套管进行了ANSYS抗挤强度模拟分析，采用均布外挤应力加载的方式。由于管材抗挤强度与抗内压强度相差甚微，通过查取《井下作业数据手册》得到了相同尺寸套管的API标准给定的抗内压强度值，并绘制成如图10所示的曲线。

图10 ANSYS计算的套管抗挤强度与API标准值对比

由图10知：ANSYS计算的套管抗挤强度与API标准给定的强度比较吻合，其中3个数据点几乎重合；当井眼较深时或是原场地应力分布较不均匀时，除了加大钢级，也可以采取增大套管壁厚的方式来提高套管的抗挤强度。

4.4 非均质率对套管抗挤强度影响

本文选取177.8 mm×8.05 mm N80套管进行ANSYS分析，非均质率变化范围为1.0～1.5。分析结果如图11，可以看出：随着非均质率加大，套管抗挤能力急剧下降。非均质率超过1.1时，下降幅度变缓，接近水平，趋近于10 MPa。因此，非均质地应力对套管抗挤能力的影响非常大，很容易发生屈曲变形，造成套管缩径、挤毁。