注重思维训练 促进思维发展

陈胜利

教而有法，教无定法。随着教育观念的改变，新的数学教学模式层出不穷，标新立异。或是导练结合，或是实验演示，或是注重参与，或是寓教于乐，殊途同归终是不离对学生能力素质的培养。我们要充分挖掘教材中培养思维能力的因素，以疑点为契机，让学生的思维在“质疑—说疑—释疑”中逐步发展深入。以下是我在课堂教学中渗透学生思维能力训练的一些浅知拙见。

一、新旧知识过渡设计问题，引发思维

学生的学习兴趣直接影响着一节课的教学效果，学生对学习的兴趣，不仅表现在对数学知识内在“美”的切身体会，还表现在课堂伊始是否投入学习，参与学习。有经验的教师总是善于去激发学生的学习兴趣，在教师的“导演”下，不知不觉地进入教师预定的“圈套”。因而我认为在新旧知识连接的复习导课中，应适当设计悬念，让学生“跳一跳可以摘到桃子”。以激发他们探知兴趣和求知欲望。如教学“通分”时，我设计了三道分数大小比较的复习导入题：

（1） （ ） ；（2） （ ） ；（3） （ ）

在这三道题中，（1）、（2）题学生可以根据已学的知识进行比较，但第（3）题不能，我以启发的问题“同学们能运用所学的知识通过转化来比较他们的大小吗？”设计学习新知的悬念。另外，创设适宜的教学情境，使学生在好奇、好胜的心理状态下进入学习的高潮。

二、授新时重点难点处，训练思维

1.启其疑。学贵于疑。思考是训练学生思维素质的一种好形式，学生只有对所学知识进行阅读、思考、解疑，置身于老师的问题情景之中，才能最大限度让其思维得以拓展、深入。如我在教“较复杂的求一个数的几分之几是多少”的分数应用题时，我根据教材内容，让学生在学习思考中完成下列学习目标：解答分析分数应用题的关键是什么？如何判断谁是单位“1”的量？已知还是未知？根据单位“1”的量是否已知来决定用什么方法计算（算术解）？所求量跟已知分率是否相对应？如何找对应分率？让学生带着这些问题自学，然后把思考中的疑问提出来，教师加以点拨说明剖析，以上是学生“学习—思考—质疑—解惑”从而掌握方法的过程，就是学生通过思维学习新知的过程。

2.疏其堵。学生在思维过程中，有时会出现阻塞，想不下去或想错了，此时，教师扶他一把，或提示有关背景知识，或指点途径方法，或诱导分析，使其思路畅通。我在教“异分母分数相加减”时，先让学生尝试练习 + =（ ），个别学生会填上 ，显然，学生是如此计算 + = = ，把分子相加作分子，分母相加作分母。如何纠正学生的错误思路排除误区呢？我先出示一组题：

由于我紧扣分数的基本性质帮其理清障碍，巧除“雷区”，使其获得正确的计算方法，同时其分析、比较、综合以及抽象概括能力无疑得到很好的培养和发展。

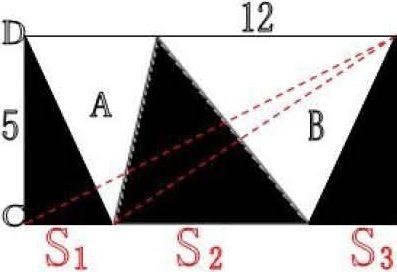
3.促其思。成功的一堂课将充分调动学生的注意力，与教师的思维线索同步，师生达成思维的共鸣。现在的教学目标不限于对知识的理解和掌握，还应该培养学生学会一些数学方法与策略。如：求图中阴影部分的面积（单位：厘米）

解题时。若循着S阴=S1 +S2+S3 思考，思维必将进入“死胡同”。但若变换角度，从整体分析把握会收到柳暗花明的奇妙效果，其解显然易见：12×5÷2=30（平方厘米）图中三个三角形的底之和恰好是长方形的长，而长方形的宽又是三个三角形的高。另外：还可引导学生根据等底等高的三角形相等，通过填画辅助线，变成是求⊿ABC的面积。这样，在教学中教会学生多角度分析解题思路，全面整体把握，注重知识迁移，对于培养学生思维的灵活性、敏捷性，是大有裨益的。

三、巩固新知设计练习，活跃思维

如何使学生把所学的新知识运用到不同的解题中去消化、巩固，必须精心设计一些问题，遵循“统一要求，分层设计；统一布置，照前顾后”的原则，让学生形成认识的坡度，使这些坡度成为巩固知识，发展思维的阶梯，使学生的思维流程在“发展——提高——深化”中得以优化。