多元智能化在数学教学中的初步应用与研究

韩富荣

摘要：当代教育不再是单一的知识传授，而应注重多元智能的渗透，在教学中更应着眼于培养学生的能力向多元化发展。

关键词：多元智能，多元化

多元智能（Multiple Intelligences）理论最早是由美国哈佛大学教育研究院的心理发展学家霍华德 加德纳（Howard Gardner）于1983年提出的。传统意义上的中学教育只注重学生接受应试教育，也就是强调学生在数学、语文（即：逻辑和语言）两方面的发展，让学生掌握书本上的基本概念、基本理论，而忽视学生的其他智能。导致中学教育把学生都培养成一个模式：好好学习，天天向上的好孩子，循规蹈矩，恪守成规……加德纳的理论认为人的智能是全面的，多元化的。过去对智力的定义过于狭窄，未能正确反映一个人的真实能力，人的智力应该是一个量度他的解题能力的指标。根据这个定义他提出：人类的智能至少可以分成八个范畴：语言智能、逻辑数学智能、空间智能、肢体运作智能、音乐智能、人际智能、内省智能和自然探索智能。对于中学生来讲，由于多元智能理论有助老师从学生的智能分布去更了解学生，我们可以利用多元智能理论来发掘资优学生，进而为他们提供合适的发展空间，使他们自由而全面的发展。也可以利用多元智能理论来扶助暂困生，并因地制宜的采取适当的教育方法对其特长予以大胆肯定和充分的鼓励，使其充分发挥特长发展强项。中学数学新课标指出：要使数学教育面向全体学生，人人都能获得必需的数学、不同的人在数学上得到不同的发展……因此，在数学教学中我们更要注重学生多元智能的培养与开发，鼓励学生通过主动的观察、实践、猜想、验证、推理与交流等数学活动去获得知识解决实际问题，感知身边的现实世界。

一、教学环节中多元导入的运用

数学是相对抽象的学科，教学中难免会陷课堂于枯燥、晦涩的尴尬境地。多元化导入，将数学问题用生活中形象生动的事例导入往往会帮助孩子们理解初次接触的数学现象，对我们的教学大有裨益。例如：在三角形的三边关系内容引入时，我不急于给出三角形，而是先给孩子们出示两根长度相等的橡皮筋，然后拉伸一根，让他们观察构成了什么图形，同学们很容易回答：是三角形。紧接着提示大家，正因为橡皮筋伸长了，才形成了三角形。原本这两根橡皮筋长度相等，但构不成三角形；可后来一根变长了，也就是两边之和大于第三边了，才构成了三角形。所以构成三角形前提条件必须是：三角形两边之和大于第三边。接下来，在求三角形第三边范围问题上我采用极限思想让孩子们大胆联想：两根长度不等的木棒一端用钉子钉上，另一端用橡皮筋连接，欲构成三角形，必须使橡皮筋位于两种极限情形之间，也即是，当两根木棒拉伸橡皮筋至两木棒在一条直线上时（此时橡皮筋的长度等于两根木棒长度的和）和当两根木棒重合于一条直线上时（此时橡皮筋的长度等于两根木棒长度的差），同学不难看出位于这两种极限情形之间才能构成三角形。故而，三角形第三边的范围应为大于两边之差、小于两边之和。

二、打破传统教学模式，实现多元化探究教学

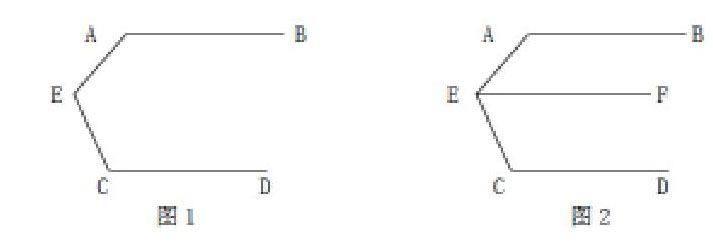
传统教学中，中学课堂采用老师一味地讲，填鸭式教学，学生只带耳朵来到课堂。这种教学模式使学生缺乏主动性、创造性和积极参与意识，老师教得死板学生学得生硬，无法灵活面对变幻多样的题型，更不用说将来面对错综复杂的现实世界。这就亟待我们改变现状，打造出多元化的新课堂教学模式，让学生积极参与进来，地位从听众变成课堂的主人。这是一道几何证明题：如图1，线段AB//CD，AE与CE相交于点E，求 ？此处刚刚学完平行线知识，学生必然会首先想到用“三线八角”知识点来解此题，容易用最常规的方法，过点E做AB的平行线EF//AB，如图2所示，利用两次同旁内角，得证。

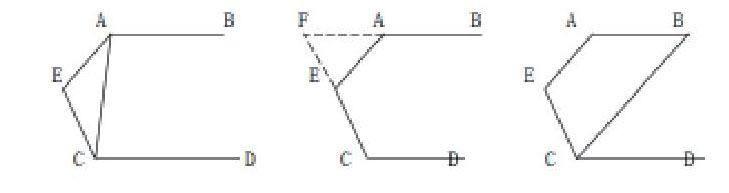
如果教师这时戛然而止的话，学生只学到一种方法，仅限于用平行线知识，从前学过的东西毫无涉及。在新课堂中，我们为什么不将主动权交给学生，充分调动其活跃的思维、想象如果教师再稍加启发，学生还会想到延长CE和BA使其相交，利用平角定义来证明，如图4；亦或有学生想到作AE平行线的方法来证，如图5……这样一来不仅鼓励学生大胆尝试多种方法解题，而且顺便复习了以前学过的知识点，使得尽可能多的学生积极动脑思维，主动参与到课堂中来，也会使尝试多种方法的学生对自己和别人的解题思路印象更加深刻。

三、多元化数学应用有助于提高学生的实用意识

义务教育阶段的数学学习应使学生充分认识到现实生活中蕴含着大量的数学信息，实现在现实世界中有着广泛的应用面对实际问题时，能主动尝试着从数学角度运用所学的知识和方法寻求解决问题的策略，并探索其应用价值。在教学中有这样一道应用题：某人的移动电话可选择两种收费办法中的一种，甲种收费办法是，先交月租费50元，每通一次电话再收费0.40元；乙种收费办法是，不交月租费，每通一次电话收费0.60元。问：每月通话在什么范围内选择甲种收费办法合适？每月通话在什么范围内选择乙种收费办法合适？在讲解这道题时，我并没有急于让学生给出答案，而是事先布置作业，让学生回家做一项调查：问问家里的人的手机都使用什么收费标准？然后自己整理数据，总结一下究竟哪种收费方法最省钱？第二天学生到校后把自己的结果拿来，老师对比发现，同一种收费方法有的同学认为最省钱，有的同学却不是？那么为什么会有不同结果呢？让同学们先讨论，自己尝试发现问题症结？这时就会有同学顿悟：一种收费方式不一定永远最省钱，而是在某一范围内才最省钱，这就是取值范围的重要性所在。老师再问：那么，用什么办法来比较，那种方式最省钱呢？这个取值范围又如何确定出来呢？鼓励学生多种方法。这样一来，一道看似简单的不等式应用问题，不仅锻炼了学生的统计观念、比较原则、数感、谈论参与意识，而且充分发掘了学生的语言只能、肢体运动只能和自然探索智能。从而使学生更热爱数学，增强了数学应用意识。

四、多元智能有助于学生数学思想的渗透

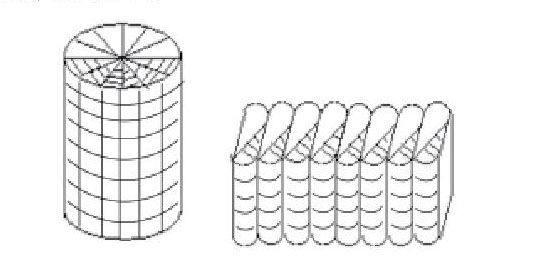
初中阶段的数学教学不应囿于初中阶段知识结构体系，涉及高中或大学的数学思想也应给予适当的渗透，只有这样才能保证知识体系的多元化和可持续发展，为高中数学学习乃至大学数学研究打下坚实的基础，同时也可以激发学生们对数学的强烈求知欲和好奇心。例如在圆柱体体积的探究学习中，我采用分割法逼近圆柱体的体积，首先把圆柱体想象成若干“比萨饼”摞起来，先分割每张“比萨饼”，即分割平面圆，然后重新组合近似看作长方形，再将“比萨饼” 摞起来，长方形就变成了长方体，求圆柱面积就可以通过求近似长方体的体积来解决。这种方法在不知不觉中渗透了高等数学中的微积分思想：无限细分、无限积累、近似代替、求和，一气呵成。不仅生动而形象的增加了学生的空间想象能力，也渗透了大学课程中的微积分思想。简明易懂，直观形象。同时，也培养了学生从二维平面到三维空间的扩展能力，为高中立体几何课程的开设做了良好的铺垫。

现阶段在新课标的指导下，数学教学正乘着改革的东风日益多元化，成熟化，完善化。多元智能理论也循序渐进走进我们的课堂，遍布我们的教学环节：教学导入的多元化，合作探究的多元化，习题处理方式多元化，评价体系的多元化……让我们的学生在多元智能理论中体验到学习的乐趣，体验成功的快乐，发现自身的特长，增强学习的信心。对于我们教育工作者，多元智能理论更有助于形成正确的智力观、转变我们的教学观、转变我们的学生观、形成正确的发展观。这样的教学才能使不同的学生在数学学习中得到不同程度的进步，得到最大限度的全面发展，为择业与未来发展奠定坚实基础。

五、多元思想有助于学生对类比思想的理解

七年级上讨论的一元一次方程的应用问题一向使学生苦于无从下手，在教学中若采用类比的数学思想，问题便可轻松易学、迎刃而解。比如：工作量问题，尤其是其中的“单位1”问题，学生出错率极高，倘若我们在教学中做如下类比，工作量问题就会豁然开朗了。如：一项工程，甲队单独做需12天，乙队单独做需18天，如果两队合做6天后，余下的再由甲队单独做多少天可以完成？在这道题中，工作量可以类比为行程问题中的路程，而工作效率则可以类比为形程问题中的速度，时间二者相通，这样一来，两个问题就可以归结为同样的方法来解决了，因为学生对路程、时间、速度公式是熟知在先的。两个问题的类比可用如下关系揭示： ，借助此种类比思想，方程的等量关系就一目了然了。同样地，很多应用问题也可借助类比的数学思想来帮助分析，如：水流问题和风速问题的类比：船在顺水和逆水中的速度分别为 ，而飞机在顺风和逆风时的速度分别为 ；利润率问题和利息率问题的类比： ，而 ；打折问题和裁员问题的类比等等。我们在分析时都可以类比归结为同一本质的问题，采用同样的分析方法来解决，在教学中可以循序渐进地培养学生类比的数学思想方法，锻炼学生自主探究应用题解题方法的能力。