裂缝性页岩气藏水平井产能预测模型

徐兵祥，李相方，HAGHIGHI Manouchehr，张 磊，龚 崛，葛涛涛

(1.中海油研究总院新能源研究中心，北京100027;2.中国石油大学石油工程学院，北京102249;3.阿德莱德大学澳大利亚石油学院，SA5005)

页岩气商业化开发主要依赖于水平井钻井技术和多级压裂工艺的发展［1-3］。复杂的完井方式与页岩低孔低渗、含吸附气等特点使页岩气产气规律呈现新的特点:长期非稳态流动［4-5］;线性流动［6-7］;解吸气对产量贡献。因此常规递减曲线［8-11］已不适合页岩气藏。页岩气渗流模型的发展经历了由径向流模型［12-13］向线性流模型［14-21］的转变，线性流模型也由最初仅考虑压裂区产量贡献的SRV模型［14-18］到综合考虑压裂区和未压裂区产量贡献的复合气藏模型［19-21］。目前该复合气藏模型假设未压裂区为单孔系统，未考虑可能存在的天然裂缝的影响。笔者基于未压裂区双重孔隙特点，建立页岩气多级压裂水平井产能预测模型，为页岩气开发动态预测提供理论方法。

1 物理模型建立

在均质油气藏中，水力压裂一般会诱导出平板双翼裂缝，而在裂缝性油气藏中，水力诱导裂缝能够与天然裂缝发生沟通、耦合，形成复杂的裂缝网络系统。多级压裂水平井物理模型有以下3种情况:

(1)“平板双翼裂缝”型，多存在于均质油气藏中。如图1(a)所示，沿水平井筒分布着多条垂直裂缝，裂缝呈平板状。

(2)“体积压裂”型，存在于裂缝性油气藏中。如图1(b)所示，水力压裂诱导形成复杂的裂缝网络系统，使得井筒周围存在一个体积压裂区(stimulated reservoir volume，SRV)［3，22］，该区裂缝导流能力高、基质－裂缝接触面积大，而外围未压裂改造区域储层物性差。

(3)“体积压裂”与“主裂缝”混合型［3，22］。对于加砂压裂，若储层导流能力低，携砂能力有限，大量支撑剂会分布在井筒附近裂缝中，形成高导流能力主裂缝。如图1(c)所示，沿水平井筒分布着多条主裂缝，主裂缝之间分布着许多诱导裂缝。

对于天然裂缝性页岩气藏，图1(b)、(c)两种模型均可能存在。图1(b)模型可用双重介质复合气藏(压裂区与未压裂区)进行描述。图1(c)模型中压裂区包括含支撑剂高导流主裂缝与不含或微含支撑剂裂缝，主裂缝对气井初期产量影响很大，但在页岩气很长的生产周期内，产量主要受基质物性影响，这里将主裂缝与体积压裂区诱导裂缝一起考虑，取其平均效果。经过这样处理后，图1(b)、(c)中模型可用相同数学模型进行描述，只是裂缝渗透率意义不同。

2 数学模型及其求解

2.1 基本假设

图2为双孔复合气藏模型示意图，包括内区(体积压裂区，1区)和外区(未压裂区，2区)，中间为一口水平井。储层包括裂缝系统与基质系统。假设:

(1)气藏为双孔系统，基质块为平板状，均质、等厚、等温;

(2)裂缝到井筒、内区基质到内区裂缝、外区裂缝到内区裂缝、外区基质到外区裂缝的流动均为线性流动;

(3)气藏为单相气生产，不考虑水平井端部流体流动;

(4)考虑吸附气解吸对产量的影响;

(5)不考虑表皮系数与井储效应影响。

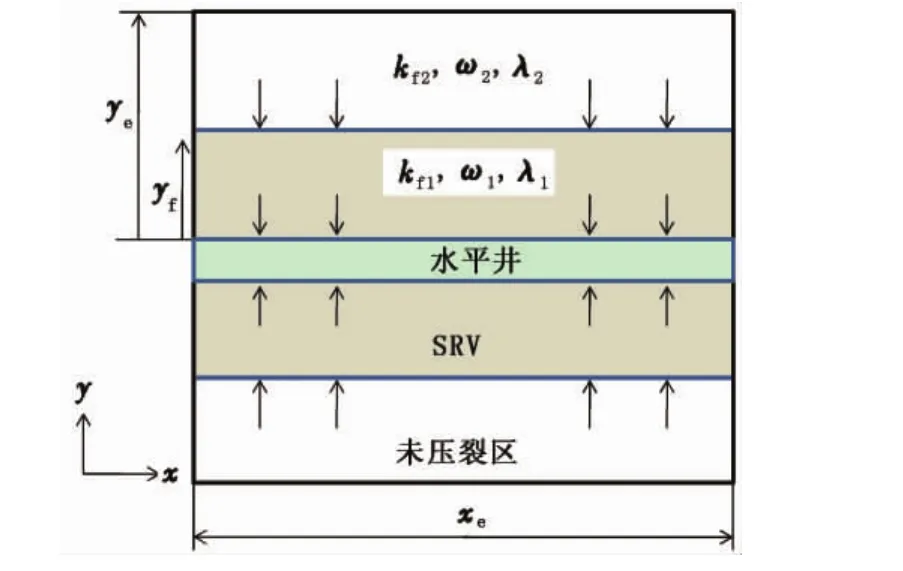
图2 双孔复合气藏模型Fig.2 Dual porosity composite reservoir model

2.2 连续性方程及边界条件

运用拟压力与拟时间函数考虑气体参数随压力与时间的变化，同时运用修正的总压缩系数Ct来考虑基质孔隙中气体解吸［23］。

拟压力为

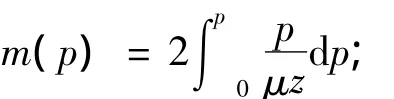
拟时间为

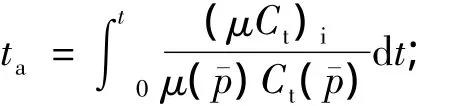
修正的总压缩系数为

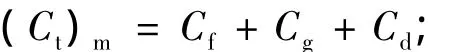
解吸压缩系数为

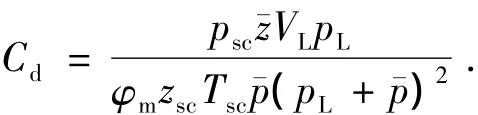
式中，p为压力，MPa;psc取0.1 MPa;¯p为平均地层压力，MPa;μ为黏度，mPa·s;z为气体压缩因子;zsc为0.1 MPa、25℃ 下气体压缩因子;¯z为平均地层压力对应的气体压缩因子;m(p)为拟压力，MPa2·(mPa·s)－1;ta为拟时间，d;Ct为综合压缩系数，MPa－1;Cf和Cg分别为岩石与气体的压缩系数，MPa－1;Cd为解吸压缩系数，MPa－1;Tsc取25℃;pL为兰式压力，MPa;φm为基质孔隙度;μ(¯p)为平均地层压力下气体黏度，mPa·s;Ct(¯p)为平均地层压力下综合压缩系数，MPa－1。

无因次变量定义见表1。

表1 无因次变量定义Table 1 Definition of dimensionless variable

根据无因次产量与压力的关系，得到

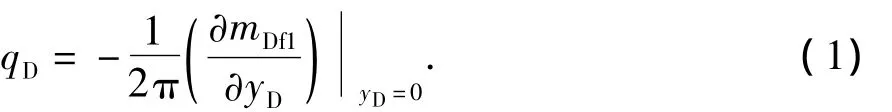
(1)1区裂缝和基质无因次偏微分方程与边界条件分别为

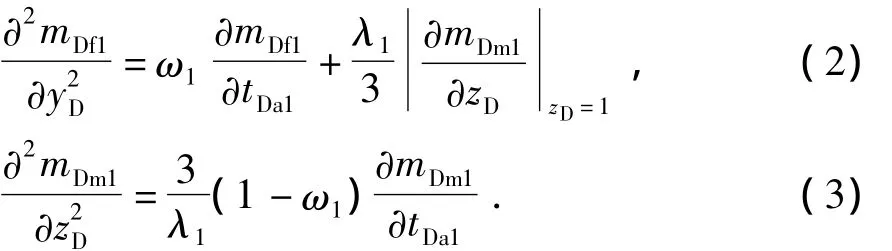
(2)2区裂缝和基质无因次偏微分方程与边界条件分别为

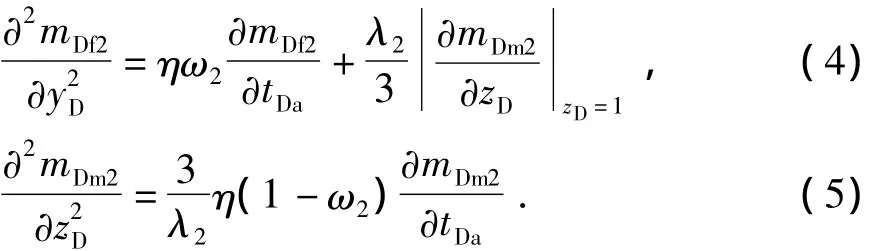
初始条件:气藏各处原始地层压力相同，因此拟压力函数相等，

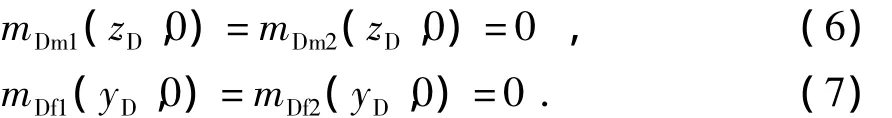
内边界条件:假设气井以定井底压力生产，因此任何时间井底拟压力函数相同。

内外区交接面处条件:假设两区交接面处压力与气体流速相等，由于温度压力相等时气体黏度也相等，因此流速相等，

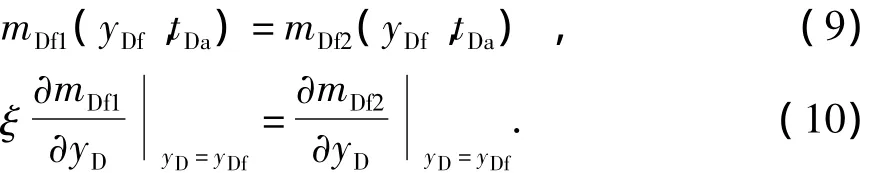
外边界条件:此处分别考虑无限大边界与封闭边界两种情况:

2.3 基质方程的解

内区(1区)控制方程及边界条件为

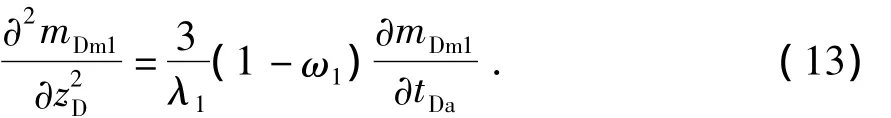
初始条件为

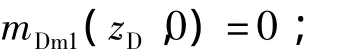
内边界条件为

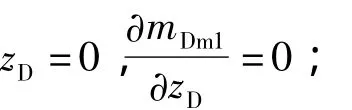
外边界条件为

zD=1，mDm1=mDf1.

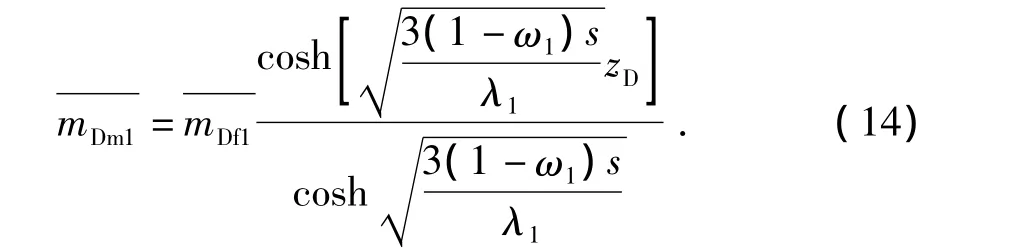
类似的可得到2区的Laplace空间解为

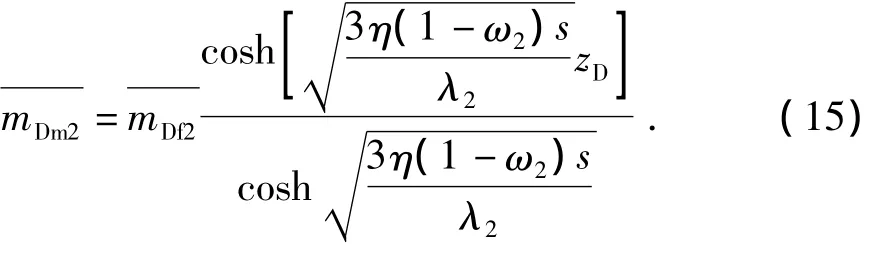
2.4 裂缝方程的解

将基质方程的解代入裂缝方程中，得

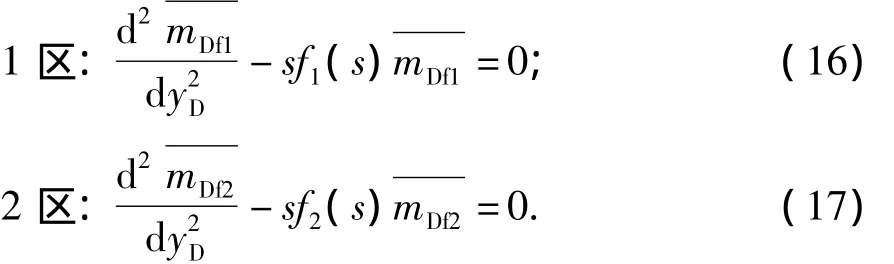
其中

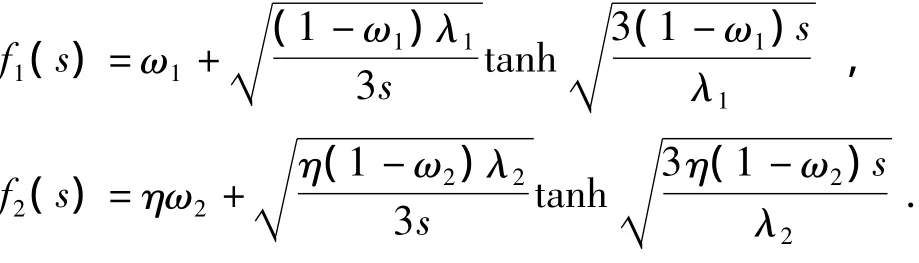
根据产量与压力关系式(1)，得到Laplace空间关系为

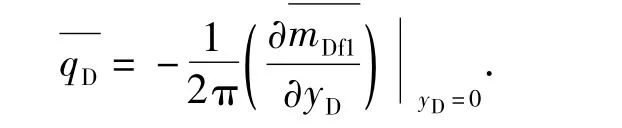
根据上面定解条件，求得不同外边界条件下定井底压力laplace空间产量解。

封闭边界解为其中

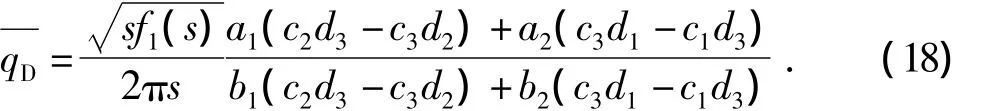
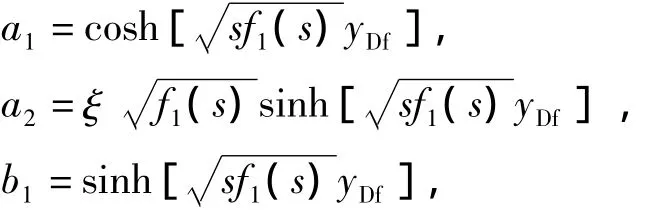
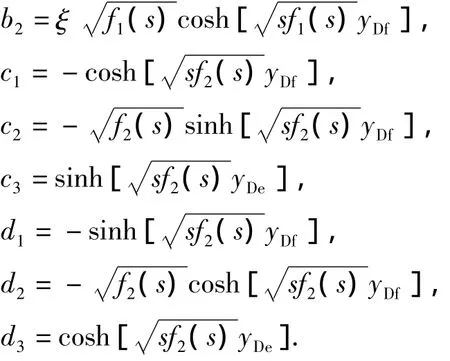
无限大边界解为

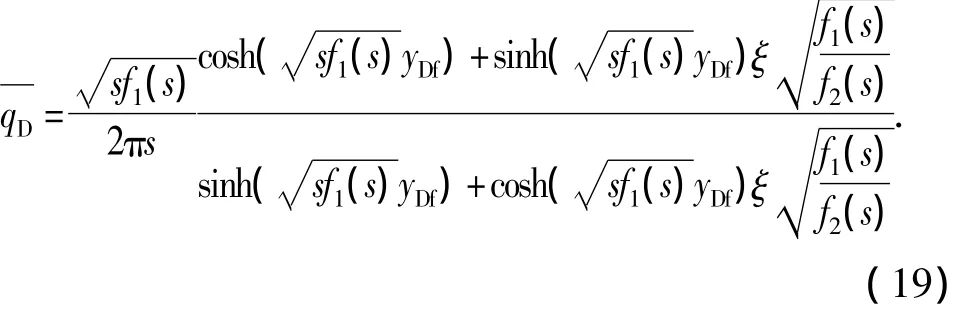
3 新模型验证

3.1 与其他解析解对比

建立的页岩气新模型假设内区和外区均为双孔系统，该模型解析解不仅适用于裂缝性页岩气复合气藏，同时若改变 ω1、ω2、ξ、η、yDf和 yDe等无因次参数值和条件，还可适用于其他页岩气模型或假设情况，如单孔复合气藏(内区双孔+外区单孔)、SRV模型(双孔，仅含有内区)和均质气藏(单孔系统)。若令ω2等于1，意味着外区气藏属于单孔系统，这与Brohi等［19］建立的模型假设相同，解的形式也完全一致，其他解形式转化如表2所示。这既证明了新模型及解析解的正确性，也说明了该模型的普遍性，可以用来描述均质气藏线性流动、双孔瞬态线性流动模型(SRV模型)和单双孔复合气藏模型。

表2 不同线性流动模型解Table 2 Linear flow solutions for different models

3.2 数值模拟验证

给出的解析解既适用于气井情况，也同样适用于单相液情况，此时只需采用压力、时间分别替换拟压力、拟时间。为了验证解析解的可靠性，运用E-clipse三维差分数值模拟器建立单相气和单相液(水)2个双孔介质复合地层数值模型进行误差分析。为简化模型，不考虑吸附气的影响。由于E-clipse软件双孔模型中假设基质到裂缝为拟稳态窜流且为三维径向流，而上述解析解假设基质到裂缝为非稳态且为线性流，为保证两种模型假设一致性，数值模型中需要定义一维渗透率(有针对性给定某一方向渗透率，其他方向赋值为零)，以满足线性流动假设;另外为了减小由拟稳态窜流代替非稳态窜流而引起的误差，需要测试给出一个合适的基质形状因子σ值。

数值模型模拟液体时，输入参数为:kf1=10×10－3μm2，kf2=1 × 10－3μm2，km1=km2=0.01 × 10－3μm2;φf1=0.0005，φf2=0.0001，φm1=φm2=0.05;σ1=0.011 m－2，σ2=0.00011 m－2;yf=22.86 m;ye=304.80 m;xe=1219.20 m;h=30.48 m;Bw=1;Ct=5.07× 10－4MPa－1;μ =0.607 mPa·s;pi=55.16 MPa;pwf=10.34 MPa。模拟气体时，输入参数为:kf1=0.01 ×10－3μm2，kf2=0.001 × 10－3μm2，km1=km2=0.000 2 × 10－3μm2;φf1=0.000 5，φf2=0.000 1，φm1=φm2=0.05;σ1=0.215 m－2，σ2=0.001 1 m－2;yf=30.48 m;ye=304.80 m;xe=1 219.20 m;h=30.48 m;T=413.9 K;Ct=9.85 ×10－3MPa－1;μ =0.0294 mPa·s;pi=55.16 MPa;pwf=10.34 MPa。

根据数值模型输入参数，对应的解析解计算参数为:对于液体，ω1=0.01，ω2=0.002，λ1=0.8，λ2=0.08，A=7.43 ×10－4m2，yDf=0.084，yDe=1.118，ξ=10，η =9.92;对于气体，ω1=0.01，ω2=0.002，λ1=320，λ2=16，A=7.43×10－4m2，yDf=0.112，yDe=1.118，ξ=10，η =9.92，Δm(p)=1.19×105MPa2/(mPa·s)。

图3为数值解与解析解对比曲线。该曲线包括线性流和边界效应两大流动阶段。从图3中可以看出解析解与数值解吻合较好。

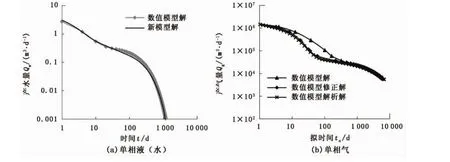
图3 数值模拟与新模型解析解对比Fig.3 Comparison of numerical simulation and analytical solution

为了方便计算，采用产量与拟时间关系进行对比。解析解产气量与拟时间的关系直接由式(18)反演得到;同时数值解产气量－时间关系需要转换成产气量－拟时间关系，计算拟时间需要已知平均地层压力。起初运用全气藏平均地层压力计算拟时间，得到图3(b)中最上面曲线。该曲线在初期、后期与解析解曲线拟合较好，而中期偏离较大。分析原因为中期平均地层压力计算不合理。初期流动主要受裂缝系统控制，整个储层裂缝系统均发挥作用，运用全气藏平均地层压力是合理的;后期流动主要受基质系统控制，运用全气藏平均地层压力也是合理的;然而在生产中期，产量主要受内区基质系统控制，压力降主要消耗在内区，若是运用全气藏平均地层压力(压力值偏大)计算气体参数会引起较大误差。因此，生产中期应采用内区平均地层压力计算气体参数，通过该法校正得到的曲线与解析解吻合较好。

4 裂缝性页岩气藏典型曲线

4.1 典型曲线及流动阶段划分

基于解析解式(18)和(19)分别建立不同λ2值时无限大与封闭页岩气藏典型曲线，如图4所示。

由图4(a)(ω1=10－2，ω2=10－3，λ1=10－3，ξ=η=20，yDf=1)可以看出，曲线流动阶段为线性流与过渡流交替。新模型与SRV模型典型曲线初期阶段重合，中后期差别较大。流动阶段达到内区边界后，SRV模型典型曲线出现骤降，呈典型的边界效应特征;新模型则出现明显的过渡流阶段，时间取决于外区窜流系数λ2，λ2值越大，过渡流持续时间越短。该过渡流呈外区裂缝－基质双线性流动特征，在双对数曲线上为－1/4斜率直线。

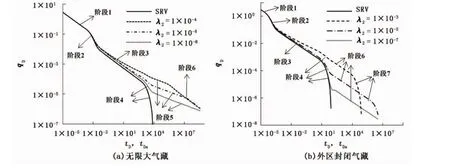
图4 不同λ2时页岩气压裂水平井产量典型曲线Fig.4 Production characteristic curves of fractured horizontal well with different λ2in shale gas reservoir

如图4(b)(ω1=10－2，ω2=10－4，λ1=10－1，ξ=η=10，yDf=0.1，yDe=10)所示，封闭性外边界气藏情况有些不同。由于封闭性气藏裂缝流动容易达到边界，因此后期过渡流之后不会出现双线性流动阶段。继内区基质边界效应之后，典型曲线流动阶段包括过渡流、外区基质线性流和外区边界效应。当外区窜流系数λ2值较高时，外区作用对典型曲线的影响有可能提前。

基于以上分析，总结出新典型曲线存在以下流动阶段:

(1)阶段1为裂缝线性流。该流动阶段包括内区与外区裂缝线性流动。裂缝渗透率与基质渗透率相比要大的多，因此早期阶段外区裂缝线性流动同样可以观察到。该阶段典型曲线呈－0.5斜率直线。

(2)阶段2为过渡流Ⅰ。该阶段可能存在两种情况:一是双线性流动，为基质与裂缝线性流动综合作用，双对数曲线呈－0.25斜率直线;二是裂缝系统边界效应，裂缝流动很快达到边界，基质系统线性流动还未形成。

(3)阶段3为内区基质线性流。该阶段内区基质流动占主要作用，双对数典型曲线呈－0.5斜率，该阶段时间取决于基质块尺寸和基质渗透率。

(4)阶段4为过渡流Ⅱ。内区基质线性流动结束后，基质边界流动开始占主要作用，同时外区也有部分供气。

(5)阶段5为外区双线性流动(无限大气藏时存在)。当外区为无限大储层时，外区裂缝线性流动与基质线性流动同时作用，形成双线性流动。典型曲线呈－0.25斜率，如图4(a)所示，该阶段持续时间随着λ2增加而缩短。

(6)阶段6为外区基质线性流。该阶段产量主要由外区基质系统提供，为外区基质线性流动控制，双对数典型曲线呈－0.5斜率。

(7)阶段7为外边界效应(封闭气藏时存在)。对于封闭气藏，当流动达到外边界时，表现为外边界效应控制，双对数曲线上无因次产量骤降。

4.2 参数敏感性分析

4.2.1 裂缝渗透率比

内外区裂缝渗透率比值ξ对典型曲线有一定影响。如图5(ω1=10－2，ω2=10－3，λ1=10－2，λ2=10－4，yDf=1)所示，当ξ值较大时，无因次产气量较低，且到达外区线性流动的时间推迟。ξ值不会改变后期流动阶段划分，但当ξ值较小时，外区气藏对产气的影响会提前，因此会影响内区基质流动阶段时间。

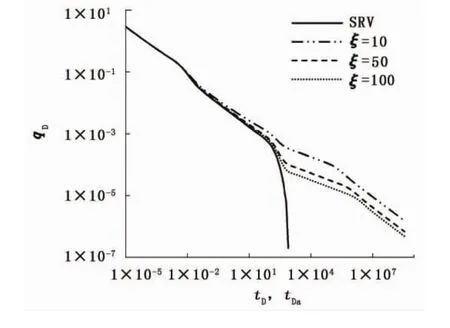
图5 无限大气藏条件下ξ值(η≈ξ)对典型曲线影响Fig.5 Effect of ξ(η≈ξ)on characteristic curves in infinite reservoir

4.2.2 气藏尺寸

内区尺寸取决于水力裂缝的延伸范围，而外区尺寸受井距以及诸如断层等地质因素影响。分别运用无因次长度yDf和yDe研究内区与外区尺寸对典型曲线影响。

图6为不同yDf和yDe对典型曲线的影响。图6(a)中 ω1=10－2，ω2=10－3，λ1=10－2，λ2=10－5，ξ= η =50，图 6(b)中 ω1=10－2，ω2=10－4，λ1=10－1，λ2=10－3，ξ= η =10，yDf=0.1。可以看出:曲线起点相同，yDf较大时，初期裂缝线性流动阶段持续较长，产量高，同时较大yDf值曲线流动阶段划分更清晰。yDf值对内区基质线性流动结束时间影响较小;外区尺寸对无因次产量影响很大，yDe值越大，无因次产气量越大;yDe值对典型曲线流动阶段、外区边界效应时间几乎无影响。

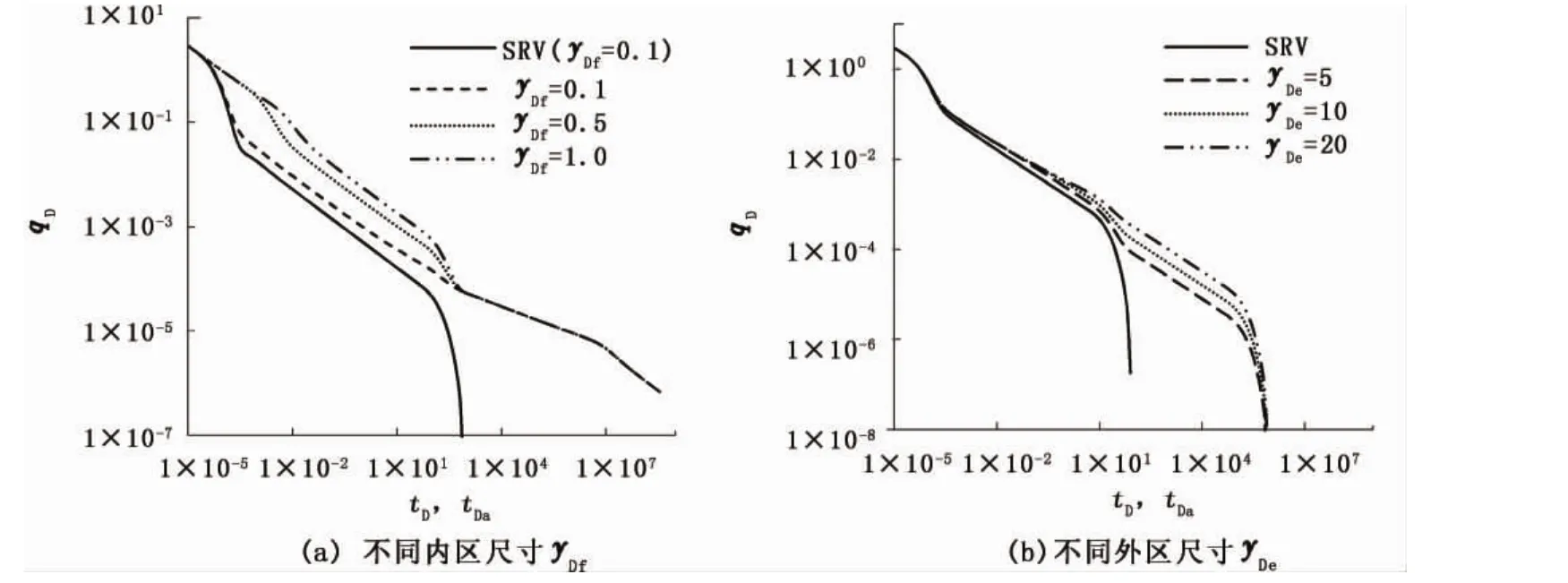
图6 气藏尺寸对典型曲线的影响Fig.6 Effect of reservoir size on characteristic curves

4.2.3 储容比

图7为储容比对典型曲线影响(λ1=10－2，λ2=10－5，ξ=η =20，yDf=0.5)。可以看出:储容比 ω1值越大，初期裂缝线性流动阶段产气量越高;不同ω2时曲线重合，原因为外区裂缝系统气体对产气贡献较基质系统气体小。储容比对典型曲线总体影响不大。

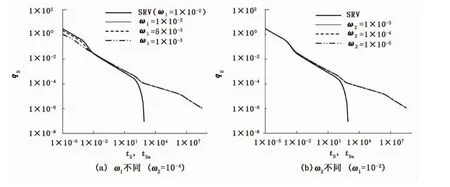
图7 无限大气藏条件下储容比对典型曲线影响Fig.7 Effect of ω on characteristic curves in infinite reservoir

4.3 未压裂区天然裂缝重要性

为了说明外区双孔系统的重要性，对比了SRV模型、Brohi模型与新模型典型曲线特征。由于新模型中ξ和η的定义与Brohi模型不同，因此采用一套有因次参数进行计算，基本输入参数为kf1=0.01×10－3μm2，kf2=0.001 × 10－3μm2，km1=km2=0.0001 ×10－3μm2，φf1=0.001，φf2=0.0001，φm1=φm2=0.1，σ1=1.07 ×10－3m－2，σ1=1.07 ×10－4m－2，λ1=λ2=1，ω1=0.01，ω2=0.001，Brohi模型取 ξ=100，η =99.1，A=9.3 ×104m2，yDf=1;新模型取 ξ=10，η =9.91，A=9.3 ×104m2，yDf=1。模型假设外区为无限大，运用不同外区裂缝渗透率与基质形状因子研究双孔系统参数对产气的影响。

图8(a)对比了不同外区裂缝渗透率下SRV模型、Brohi模型与新模型典型曲线。可以看出:典型曲线在初期重合;在生产后期，外区储层对典型曲线产生较大影响。对于SRV模型，当流动达到内区储层边界后，无因次产量qD骤降;对于Brohi模型，qD下降速率先增加，解释为内边界效应影响，继而变为直线下降;对于新模型，曲线特征类似于Brohi模型，但无因次产量qD比Brohi模型要高，且随着外区裂缝渗透率增加而增加。

图8(b)为外区基质形状因子σ2对典型曲线的影响。总体说来，新模型比SRV模型、Brohi模型无因次产量高。不同外区σ2值对过渡流Ⅱ阶段影响明显，σ2值越低，过渡流Ⅱ阶段时间越长，典型曲线呈－0.25斜率直线，解释为外区双线性流动。

外区双重孔隙特征较单一介质产气量高，即使在裂缝渗透率(5×10－7μm2)与基质渗透率处于同一数量级时或σ2值很小时也同样成立。

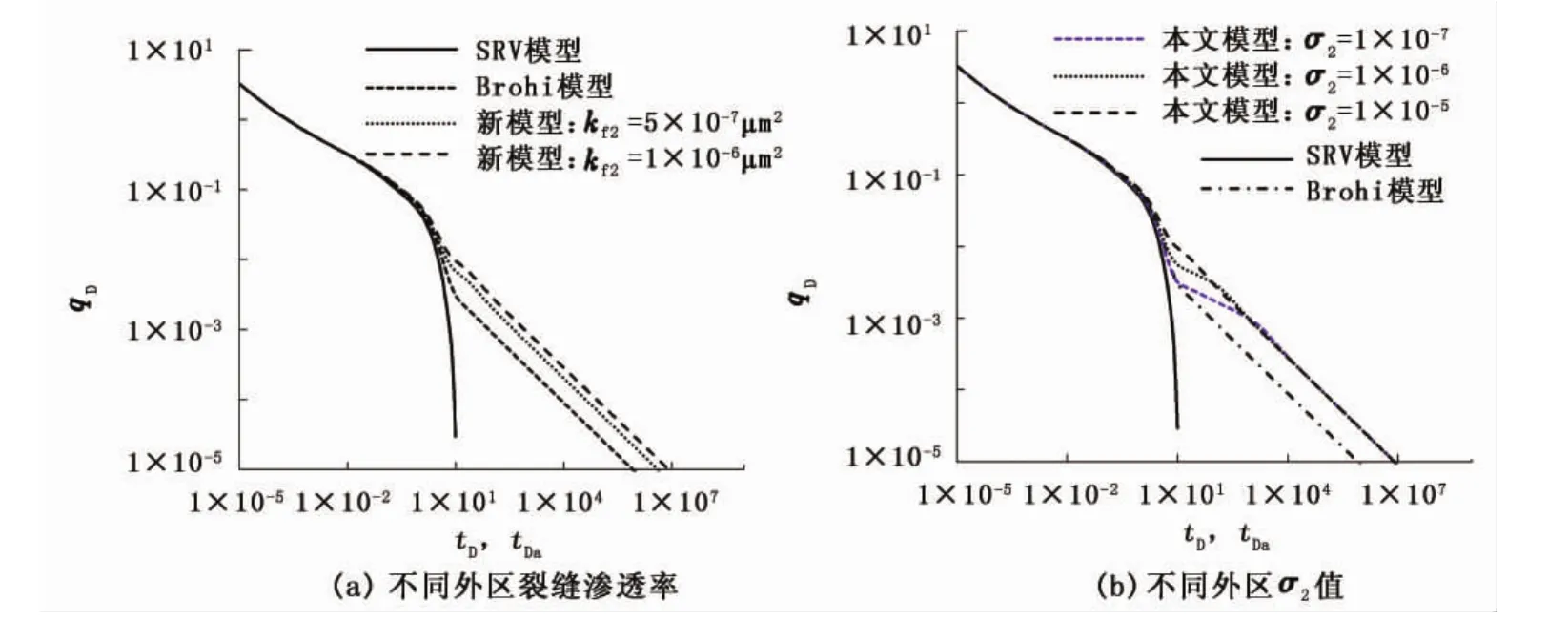
图8 SRV模型、Brohi模型与新模型典型曲线对比Fig.8 Characteristic curve comparison of SRV model，Brohi's model and new model

5 结论

(1)建立的页岩气多级压裂水平井模型考虑了未压裂区双重孔隙特征以及解吸气对产量影响。该模型适用范围广，既适用于均质气藏、双孔瞬态流动模型，又适用于天然裂缝性气藏;数值模型验证表明该解析解与数值解吻合度高。

(2)发展了新的页岩气藏产量典型曲线，总结出页岩气多级压裂水平井包含7个流动阶段，且呈线性流与过渡流交替。气藏尺寸、窜流系数、裂缝渗透率比对典型曲线影响很大，而储容比的影响不明显。

(3)未压裂区天然裂缝对页岩气后期产量具有正作用，对裂缝性页岩气藏进行产能预测时不可忽略。

致谢 感谢阿德莱德大学澳大利亚石油学院Dennis Cooke博士和Pavel Bedrikovetski教授对本研究工作的帮助与建议。

［1］ 钱伯章，朱建芳.页岩气开发的现状与前景［J］.天然气技术，2010，4(2):11-14.

QIAN Bo-zhang，ZHU Jian-fang.Shale gas development:today and tomorrow［J］.Natural Gas Technology，2010，4(2):11-14.

［2］ 李艳丽.页岩气储量计算方法探讨［J］.天然气地球科学，2009，20(3):467-470.LI Yan-li.Calculation methods of shale gas reserves［J］.Natural Gas Geoscience，2009，20(3):467-470.

［3］ CIPOLLA C L，LOLON E P，ERDLE J C，et al.Reservoir modeling in shale-gas reservoirs［R］.SPE 125530，2009.

［4］ WATTENBARGER R A，EL-BANBI A H，VILLEGAS M E，et al.Production analysis of linear flow into fractured tight gas wells［R］.SPE 39931，1998.

［5］ AL-AHMADI H A，ALMARZOOQ A M，WATTENBARGER R A.Application of linear flow analysis to shale gas wells-field cases［R］.SPE 130370，2010.

［6］ ANDERSON D M，NOBAKHT M，MOGHADAM S，et al.Analysis of production data from fractured shale gas wells［R］.SPE 131787，2010.

［7］ MOGHADAM S，MATTAR L，POOLADI-Darvishm.Dual porosity type curves for shale gas reservoirs［R］.SPE 137535，2010.

［8］ ARPS J J.Analysis of decline curves［J］.Trans AIME，1945，160:228-247.

［9］ FETKOVICH M J.Decline curve analysis using type curves［J］.JPT，1980，32(6):1065-1077.

［10］ PALACIO J C，BLASINGAME T A.Decline-curve analysis using type curves——analysis of gas well production data［R］.SPE 25909，1993.

［11］ AGARWAL R G，GARDNER D C，KLEINSTEIBER S W，et al.Analyzing well production data using combined-type-curve and decline-curve analysis concepts［J］.SPE Reservoir Res Eval＆ Eng，1999，2(5):478-486.

［12］ LEE W J，GATENSILL J M.Analysis of eastern devonian gas shales production data［R］.SPE 14506，1985.

［13］ HAZLETT W G，LEE W J，NARAHARA G M.Production data analysis type curves for the devonian shales［R］.SPE 15934，1986.

［14］ BELLO R O，WATTENBARGER R A.Multi-stage hydraulically fractured shale gas rate transient analysis［R］.SPE 126754，2010.

［15］ BELLO R O.Rate transient analysis in shale gas reservoirs with transient linear behaviour［D］.Texas:Texas A ＆ M U，College Station，2009.

［16］ BELLO R O，WATTENBARGER R A.Rate transient analysis in naturally fractured shale gas reservoirs［R］.SPE 114591，2008.

［17］ BELLO R O，WATTENBARGER R A.Modeling and analysis of shale gas production with a skin effect［R］.CIPC 2009-082，2009.

［18］ EL-BANBI A H.Analysis of tight gas wells［D］.Texas:Texas A ＆ M U，College Station，1998.

［19］ BROHI I，POOLADI-DARVISH M，AGUILERA R.Modeling fractured horizontal wells as dual porosity composite reservoirs-application to tight gas，shale gas and tight oil cases［R］.SPE 144057，2011.

［20］ BROWN M，OZKAN E，RAGHAVAN R，et al.Practical solutions for pressure transient responses of fractured horizontal wells in unconventional reservoirs［R］.SPE 125043，2009.

［21］ OZKAN E，BROWN M，RAGHAVAN R，et al.Comparison of fractured horizontal-well performance in conventional and unconventional reservoirs［R］.SPE 121290，2009.

［22］ CLARKSON C R，PEDERSEN P K.Tight oil production analysis:adaptation of existing rate-transient analysis techniques［R］.CSUG/SPE 137352，2010.

［23］ BUMB A C，MCKEE C R.Gas well testing in the presence of desorption for coalbed methane and devonian shale［J］.SPE Formation Evaluation，1988，3(1):179-185.