页岩储层地应力预测模型的建立和求解

邓金根，陈峥嵘，，耿亚楠，刘书杰，朱海燕

(1.中国石油大学油气资源与探测国家重点实验室，北京102249;2.中海油研究总院，北京100027)

目前，常规能源的开发和利用已逐渐不能满足现代工业的发展需要，勘探开发的重点投向了难以开采的页岩气。页岩储层是一种低孔隙度和特低渗透率的致密储层，其生产完全依赖于压裂效果。对页岩进行压裂施工必须对页岩起裂的规律有足够的认识，其中地应力模型是指导页岩压裂施工的极为重要的理论基础。目前地应力预测模型大部分建立在地层均质各向同性的基础上，而页岩储层具有较强的非均质性和各向异性。Thiercelin［1］讨论了线弹性的横观各向同性地层地应力的计算模型，Higgins［2］在研究 Baxter页岩地层的地应力时分别应用了各向同性和横观各向同性的地应力计算模型，并对二者进行了计算和比较。目前，多数学者的理论都只考虑上覆地层压力和构造应力的影响，对地应力的描述并不全面，因此并不能完全描述横观各向同性地层地应力的特性。笔者在前人理论研究的基础上，结合渗流和孔隙压力的影响建立考虑页岩储层横观各向同性的地应力模型。

1 页岩本构特性

页岩由于其沉积历史的特殊性［3］通常具有良好的分层结构，在构造和组成上呈连续变化，因此岩石的性质在平面和垂向上会有区别，页岩岩石呈现出横观各向同性的特性［4-5］，其岩石力学性质也表现出横观各向同性［6］，即页岩储层水平方向是各向同性的而垂直方向则表现为各向异性(图1)。因此，对页岩储层可通过横观各向同性模型进行研究。

图1 页岩横观各向同性单元体Fig.1 Element of shale representing transversely isotropy body

对于横观各向同性的页岩，应力和应变之间的本构方程可通过修正后的胡克定律［7］表示为

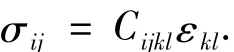
式中，σij为二阶应力张量的分量形式，MPa;εkl为二阶应变张量的分量形式;Cijkl为四阶弹性刚度张量的分量形式，MPa;i，j，k，l=1，2，3。

二阶应力张量和二阶应变张量实际分别都只有6个独立的分量，因此四阶弹性刚度张量可表示为6×6矩阵。根据地层的对称性，刚度张量的独立参数将减少，因此刚度张量C可表示为

对于横观各向同性地层，矩阵各参数有以下关系 C11=C22，C12=C21，C13=C31=C23=C32，C44=，其中 C66可以表示为因此可以用5个独立的变量表示矩阵C［9-10］。要完全描述矩阵C需要求得以上5个独立的参数，该5个参数［11］可以表示为

式中，ρ为体积密度，kg/m3;vPH和vPV分别为水平方向和垂直方向的P波波速，m/s;vSH和vSV分别为水平方向和垂直方向的S波波速，m/s;v45为与地层对称轴成45°的P波(m=－1)或S波(m=1)波速，m/s。

经过声波测井的测量，可求得横观各向同性的5个独立参数。则垂直和水平方向上的弹性模量和泊松比［12-13］分别为

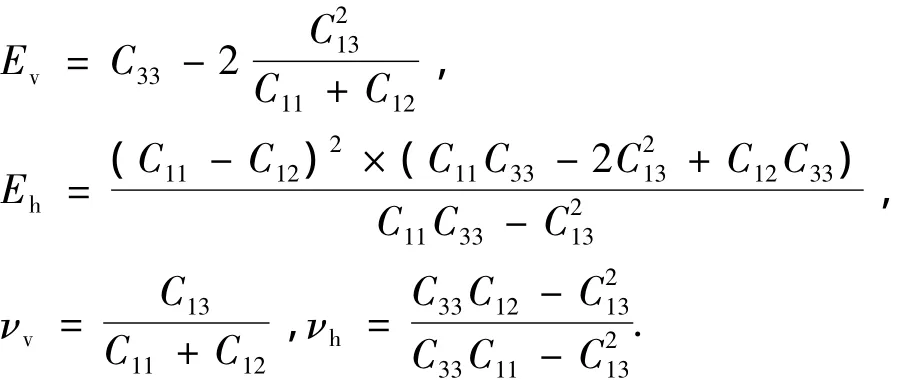
由弹性模量和泊松比表示的页岩本构模型为

其中

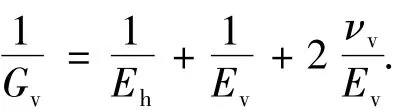
式中，σ和τ分别为作用在单元体上的正应力和剪应力，MPa;ε和γ分别为单元体上的正应变和剪应变;Eh和Ev分别为水平方向和垂直方向上的弹性模量，MPa;νh和νv分别为施加水平和垂直应变时水平应变的泊松比;Gv为垂直平面的剪切模量，MPa。

地层力学参数的测量通常通过应力应变的关系或声波速度测量得到，通过应力应变关系施加载荷测试，一般测定的是标准的力学弹性参数(如弹性模量、剪切模量和泊松比等)，声波速度测试则是测量声波的强度参数(如C11、C33和C12等)，而声波实际上也是施加在岩石上的载荷，声学性质与声波传播过程中岩石的应力应变有关。通过上述分析，这两种力学参数的测量方法等价，通过以上两种方法都可以解决岩石力学参数的测量问题，在应用过程中可根据实际情况择优使用。

2 页岩地应力预测模型的建立

地应力场中垂直地应力由上覆地层的重力产生，可通过地层的密度和厚度的积分计算得到。水平地应力的形成由地层构造运动产生的应变、不同地层之间地层性质的各向异性和非均质性及其他地质因素共同作用产生。为了预测水平地应力并构建理想的地应力模型，首先必须对所研究地层的物理力学参数的各向异性情况有足够的了解。建立页岩储层地应力模型必须考虑页岩的横观各向同性的特性。

Thiercelin讨论了线弹性各向同性和横观各向同性的地层地应力计算模型，对于各向同性地层，在平面应变的假设下，考虑上覆地层压力和构造应力的影响，水平地应力模型［1］可表示为

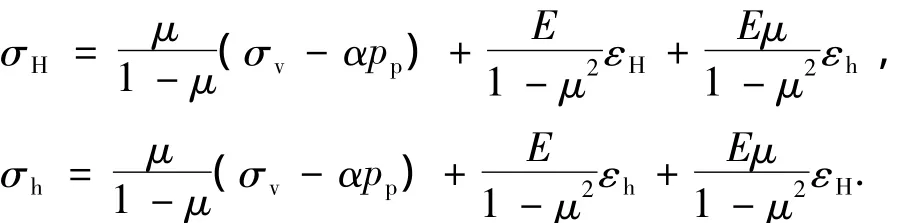
式中，σv为垂直地应力，MPa;σH和σh分别为水平最大和最小地应力，MPa;pp为地层孔隙压力，MPa;α为有效应力系数，通常取1;εH和εh分别为水平最大和最小构造应变。

对于横观各向同性的地层，Thiercelin在各向同性地应力模型的基础上考虑了地层垂直和水平方向上力学性质的差别，建立了横观各向同性地层地应力模型，即

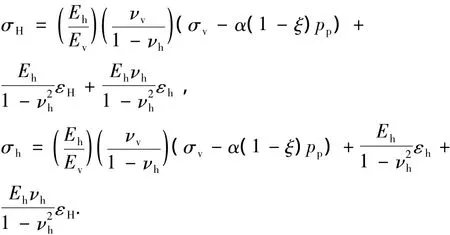
式中，ξ为渗流系数，通常取0。

其他地质条件也可能产生水平地应力，如孔隙压力的变化。结合上述因素，基于线弹性假设建立考虑地层横观各向同性、孔隙压力变化、构造载荷和渗流的有效水平地应力模型，即

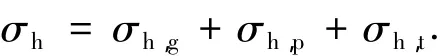
式中，σh，g，σh，p和 σh，t分别为上覆地层压力、孔隙压力变化和构造应力产生的水平地应力，MPa。

图2所示为页岩储层中影响水平地应力的各种因素。

图2 页岩储层中影响水平地应力的各种因素Fig.2 Factors of influencing horizontal in-situ stress in shale formation

如果忽略构造应力的影响，所产生的水平地应力将相同(σH=σh)，如果某一方向上存在构造作用产生的变形，则将导致水平地应力在不同方向上的应力差(σH＞σh)。相应的地应力为

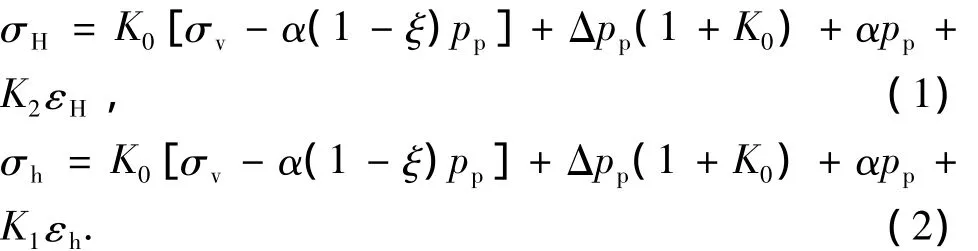
其中

孔隙压力的变化通过系数(1+K0)改变水平地应力。地质上的构造应变则通过压缩和拉伸使地应力相应的增加和减少，二者之间的比例关系可用地层的各向异性参数K1和K2表示。对于横观各向同性地层，如果不存在构造应力产生的变形，则两个水平地应力相等，而一旦考虑了构造应力，两个水平地应力将产生差别。除以上因素外，还有一些影响地应力预测的地质力学因素。该模型相对简单且所需的数据可通过测井解释方法获取，便于实际应用。

3 算 例

图3 Eh/Ev对最大和最小水平地应力的影响Fig.3 Effect of Eh/Evon the maximum and minimum horizontal in-situ stress

根据上述理论分析，编写计算机程序模拟Eh/Ev、νv/νh、孔隙压力变化对地应力的影响。模拟参数:地层平均密度为2.61 g/cm3，有效应力系数为1，渗流系数为0，εH和 εh分别为0.3和0.1。

3.1 Eh/Ev对页岩储层地应力的影响

模拟参数:垂直和水平方向的泊松比均为0.25，孔隙压力变化为0.5 MPa。图3为Eh/Ev对最大和最小水平地应力的影响。随着Eh/Ev的增大，地层的各向异性更强，水平地应力将整体变大。当Eh/Ev=4时，最大和最小水平地应力分别是各向同性(Eh/Ev=1)情况下的2.30和2.57倍，平均增加144%，因此忽略横观各向同性对地层地应力的影响，预测结果会产生较大误差，各向同性的预测结果明显偏低。

3.2 νv/νh对页岩储层地应力的影响

模拟参数:垂直和水平方向的弹性模量均为16 GPa，孔隙压力变化为0.5 MPa。图4 为 νv/νh对最大和最小水平地应力的影响。

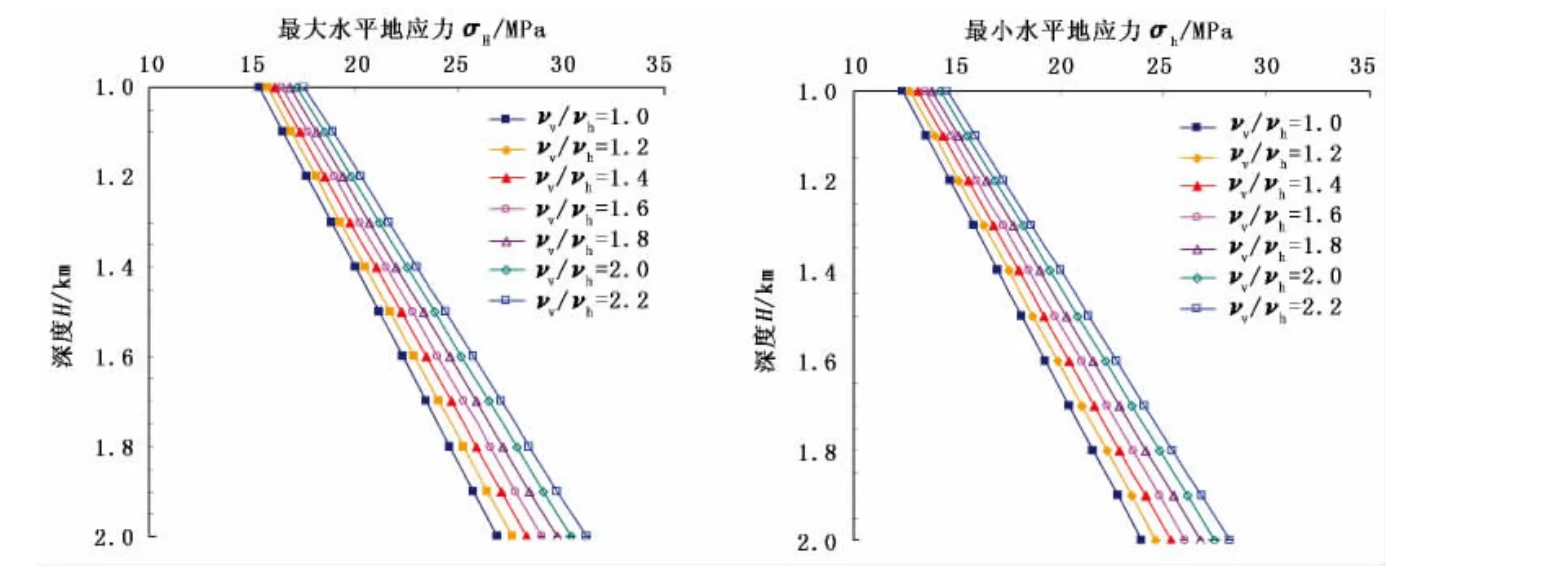
图4 vv/vh对最大和最小水平地应力的影响Fig.4 Effect of vv/vhon the maximum and minimum horizontal in-situ stress

从图4中可以看出，最大和最小水平地应力随νv/νh值增大而增大。其中，νv/νh=2.2 的最大和最小水平地应力分别是νv/νh=1时的1.15和1.18倍，平均增加16.5%。因此垂直和水平方向上的泊松比对地应力的预测亦会产生较大的影响。

3.3 孔隙压力变化对页岩储层地应力的影响

图5 孔隙压力变化对最大和最小水平地应力的影响Fig.5 Effect of pore pressure on the maximum and minimum horizontal in-situ stress

模拟参数:垂直和水平方向的弹性模量均为16 GPa，垂直和水平方向的泊松比均为0.2。图5为孔隙压力变化对最大和最小水平地应力的影响。预测地应力考虑孔隙压力的变化时，最大和最小水平地应力随着孔隙应力变化的增大而增大。其中，孔隙压力变化值为2.4 MPa时的最大和最小水平地应力分别是孔隙压力不变化时的1.13和1.15倍，平均增加13.8%。因此，孔隙压力的变化对地应力的预测也是一个不可忽视的因素。

3.4 地层升沉对页岩储层地应力的影响

一些学者在建立地应力预测模型时还考虑了地层的升沉作用(地层上升或者沉降)对地应力预测的影响［14-15］。该模型表达式为

对应的最大和最小水平地应力分别为

式中，σh，u为升沉作用影响产生的水平地应力，MPa;h为当前地层深度，m，Δh为当前地层深度与上升或者沉降之前地层深度的差值，即升沉高度，m。

模拟参数:垂直和水平方向的弹性模量均为16 GPa，垂直和水平方向的泊松比均为0.2，孔隙压力变化为0.5 MPa，其他参数同上。图6为升沉高度对最大和最小水平地应力的影响。最大和最小水平地应力随着升沉高度的增大而增大，但升沉作用对地应力的预测影响不大。

图6 升沉高度对最大和最小水平地应力的影响Fig.6 Effect of subsidence or uplift on the maximum and minimum horizontal in-situ stress

4 模型验证

选取Baxter页岩的地层参数进行模拟计算说明式(2)的准确性，将计算结果与地层瞬间闭合压力(ISIP)进行比较(图7)，可以看出本文模型和Thiercelin模型的结果都与ISIP基本一致，本文模型结果误差最大仅为1.2%，所得地应力符合Baxter页岩地应力的计算情况［2］，验证了所建立的地应力模型的准确性。相同条件下，各向同性模型计算的地应力结果与实际误差较大，并不准确，因此采用横观各向同性地应力模型更符合现场实际情况。

图7 各向同性模型、Thiercelin模型和本文模型计算的最小水平地应力与ISIP数据的比较Fig.7 Comparison of ISIP and the minimum horizontal in-situ stress computed by isotropy，Thiercelin and transversely isotropy models

5 结论

(1)水平与垂直弹性模量之比、垂直与水平泊松比的比值和孔隙压力的变化对地应力的预测影响较大，且以上3种因素增大，地应力的预测结果也将增大。升沉作用对地应力的影响较小。

(2)对于页岩储层，横观各向同性的地应力模型要比各向同性的地应力模型更能表示地层地应力的真实情况。准确计算地应力的分布对页岩储层现场的完井压裂增产设计有重要的指导作用。

［1］THIERCELIN M J，PLUMB R A.A core-based prediction of lithologic stress contrasts in east Texas formations［J］.SPE Formation Evaluation，1994，9(4):251-258.

［2］HIGGINS S，GOODWIN S，DONALD A，et al.Anisotropic stress models improve completion design in the Baxter shale［R］.SPE 115736，2008.

［3］RIVERA S R，HANDWERGER D，KIESCHNICK J，et al.Accounting for heterogeneity provides a new perspective for completions in tight gas shales［R］.American Rock Mechanics Association 05-758，2005.

［4］LINGS M L，PENNIGNTON D S，DASH D F T.Anisotropic stiffness parameters and their measurement in a stiff natural clay［J］.Geotechnique，2000，50(2):109-125.

［5］GRAHAM J，CROOKS J H A，BELL A L.Time effects on the stress-strain behavior of natural soft clays ［J］.Geotechnique，1983，33(3):327-340.

［6］SAYERS C M.Seismic anisotropy of shales［J］.Geophysical Prospecting，2005，53(5):667-676.

［7］ GAUTAM R.Anisotropy in deformations and hydraulic properties of Colorado shale［D］.Calgary:Civil Engineering，University of Calgary，2004.

［8］NYE J F.Physical properties of crystals［M］.Oxford:Oxford University Press，1985.

［9］NORRIS A N，SINHA B K.Weak elastic anisotropy and the tube wave［J］.Geophysics，1993，58(8):1091-1098.

［10］WALSH J，SINHA B，DONALD A.Formation anisotropy parameters using borehole sonic data［R］.Society of Petrophysicists and Well-Log Analysis 2006-TT，2006.

［11］HORNBY B E，HOWIE J M，INCE D W.Anisotropy correction for deviated-well sonic logs:application to seismic well tie［J］.Geophysics，2003，68(2):464-471.

［12］SAROUT J，MOLEZ L，GUEGUEN Y，et al.Shale dynamic properties and anisotropy under triaxial loading:experimental and theoretical investigations［J］.Physical and Chemistry of the Earth，2007，32(8/14):896-906.

［13］RIVERA S R，DEENDAYALU C，YANG Y K.Unlocking the unconventional oil and gas reservoirs:the effect of laminated heterogeneity in wellbore stability and completion of light gas shale reservois［R］.Offshore Technology Conference 20269，2009.

［14］SAFDAR K，SAJJAD A，HAN H X，et al.Importance of shale anisotropy in estimating in-situ stresses and wellbore stability analysis in Horn river basin［R］.SPE 149433，2011.

［15］PRIOUL R，KARPFINGER F，DEENADAYALU C，et al.Improving fracture initiation predictions on arbitrarily oriented wells in anisotropic shales［R］.SPE 147462，2011.

［16］RIVERA S R，DEENADAYALU C，CHERTOV M，et al.Improving horizontal completions on heterogeneous tight shales［R］.SPE 146998，2011.