涡轮发动机可调收扩喷管最优面积比计算及分析
2013-04-27周吉利杜桂贤
周吉利,杜桂贤
(中航工业沈阳发动机设计研究所,沈阳 110015)
0 引言
凭借性能上的优势,收扩喷管在第3、4代发动机上得到了广泛应用,如俄罗斯的AЛ-31Ф发动机、美国F35战斗机上使用的F119发动机和中国的太行发动机等均采用,但这些收扩喷管的喷口面积的调节方式却不尽相同,其结果也就有所差异。AЛ-31Ф发动机通过气动作动筒的伸缩调节喷管出口面积;F119发动机通过机械4连杆结构使喷管喉道面积和喷管出口面积形成某种对应关系;太行发动机采用气动调节的方式,通过喷管内外流的压差来决定喷管出口面积。因而在给定的发动机状态下如何确定喷管出口面积或面积比Ar(Ar=A9/A8),以使其性能最优,是选择收扩喷管出口面积调节方式的1个先决条件。
本文通过优化结构固定的可调收扩喷管推力计算模型,得到了该喷管的最优面积比控制曲线,其对应的面积比可使喷管达到最大的推力系数。通过分析影响最优面积比曲线的因素及其影响程度,并与传统利用1维等熵公式计算面积比对比,得出这种面积比计算方法在性能上的优越性。
1 推力系数计算模型及其最优值求解
影响可调收扩喷管(如图1所示)推力系数的主要影响因素包括燃气欠膨胀或过膨胀、燃气的径向速度和喷管内损失[1]。
在考虑上述因素基础上,可将喷管的推力系数描述为

在式(1)中,在发动机状态一定的情况下主机流量midф为定值。收扩喷管燃气总温T*、总压P*、比热比k、气体常数R均为定值,那么推力系数可以描述为q,即1/Ar的函数。推力系数曲线如图2所示。从图2中可见,T*=1000 K、A8=0.25 m2、喷管可用落压比π=9.54、背压 P0=101325时,式(1)所示的函数存在极大值,而且并非1维等熵喷管完全膨胀时的出口面积比。应用1维等熵公式计算的完全膨胀面积比Ar=2,而曲线中的最大值出现在Ar=1.74时。

图1 收扩喷管

图2 推力系数曲线
2 可调收扩喷管最优面积比影响因素分析
不同于简单函数,式(1)无法用求导的方式得到最大值,需要利用优化算法求解,本文使用MATLAB软件中的优化函数求取最优解。P0=101325 Pa、T*=1000 K、A8=0.42 m2、k=1.33、R=247.8时,应用优化算法对式(1)求解最优面积比和喷管可用落压比关系曲线如图3所示。从图3中可见,在1个特定发动机状态下,1个可用喷管落压比对应1个喷管推力系数最大面积比,从而绘制出1条不同落压比下最优面积比曲线。
由于无法直接得到式(1)中参数 T*、P0、A8、π、k、R对最优面积曲线直接影响的关系,需要应用MATLAB软件分析这些因素对最优面积比的影响。

图3 最优面积比曲线
2.1 A8对最优面积曲线的影响
在P0=101325 Pa、T*=1000 K、A8=0.26 m2(实线)和0.42m2(虚线)、k=1.33、R=247.8时,应用优化算法对式(1)求解最佳面积比和喷管可用落压比关系,如图4所示。图中点划线为由1维等熵公式得到的面积比。

图4 不同A8时最优面积比曲线
从图4中可见,随着落压比的增大,最优面积比也随之增大,但远远大于最优面积比,而且在大可用落压比状态下差异巨大(在落压比大于10时,面积比已经大于2)。主要原因如下:
(1)1维等熵计算的是完全膨胀的面积比,是气动面积的面积比,没有考虑机械面积与实际气动面积的差距(即流量系数的影响)[2],在喉道面积较小时尤为明显[1]。
(2)1维等熵计算公式没有考虑燃气的径向流动造成的损失,而在扩张段较短的收扩喷管中因径向分速度造成的损失不可忽略,而且径向流动所造成的损失随着喷管出口面积的增加而增大[3]。综合这2个因素,与1维等熵公式计算出的面积比相比,由式(1)优化得到的最优面积比较小[4]。
在其他条件相同的情况下,A8不同,则形成不同的最佳面积曲线。在低落压比下,大A8状态下对应的最佳面积比较大;在高落压比下,小A8状态下对应的最佳面积比较大。这是由于在小落压比情况下,燃气的主要损失来自内损失[5],由于大A8状态下喷管的内损失较小,使得喷管的面积比较大。随着落压比的增大,燃气的速度也随之加快,使得径向损失的比例增大,在相同面积比时,大A8状态下的扩张角较大,使其径向速度损失也较大,所以在相同状态下,大A8状态下面积比较小。
2.2 P0对最优面积比的影响
在 P0=101325、26436、5475 Pa,k=1.33、R=247.8、T*=1000 K时,不同A8下最优面积比曲线如图5所示。

图5不同P0、A8时最优面积比曲线
从图5中可见,不同背压下的最佳面积曲线几乎完全重合,说明背压对最佳面积比Ar的影响可以忽略不计。根据相似原理,在几何相似时,影响喷管特性的因素只有可用落压比π[5-7],这也是背压对Ar没有影响的原因。
2.3 T*对最优面积比的影响
在 P0=101325 Pa、A8=0.26 m2、k=1.33、R=247.8、T*=1000 K(实线)和2000 K(虚线)时求解对最佳面积比Ar的影响,如图6所示。

图6 2种总温下的最优面积比曲线
从图6中可见,在总温较低的情况下,同一状态面积比较大,这是由于总温温度较低时,燃气的速度小,流量大;而在总温高时情况恰恰相反。不同总温下径向损失不同,则最优面积比不同,但差异较小。
2.4 k、R对最优面积比的影响
在 A8=0.26m2、T*=1000 K、P0=101325 Pa时,不同k、R对最优面积比Ar的影响曲线如图7所示。其中实线(k=1.26、R=287.5)、虚线(k=1.325、R=287.1)。
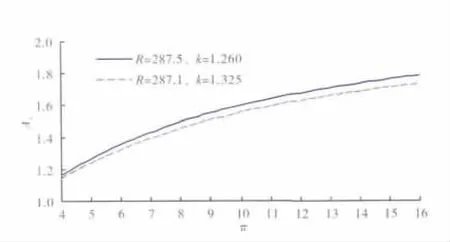
图7 不同k、R下的最优面积比曲线
从图7中可见,k、R对最优面积比Ar的影响随落压比的变化并不大。经分析得出:在 π、T*、A8、k、R中,对最优面积比Ar影响较大的是π和A8,其它因素影响不大。
3 最优面积曲线对提高推力系数的作用
在最优面积比下对应喷管最高推力系数,这是喷管在给定状态下能达到的最大理论推力系数,为收扩喷管推力系数提供了上限,与最高推力系数比较可得收扩喷管推力系数的提高潜力。假设某收扩喷管出口面积按如下控制:在面积比小于2时,由1维等熵公式确定;在面积比大于2时,面积比恒等于2。
在 A8=0.26和 0.42 m2、T*=1000 K、k=1.33、R=247.8时,采用上述控制方法得到的推力系数与最优推力系数的关系如图8所示。图中推力系数均由式(1)求得。

图8 控制推力系数与最优推力系数的关系对比
从图8中可见,喷管可以达到的最大推力系数随着落压比的增大而减小,在相同状态下,最优推力系数始终大于选用1维等熵公式控制的推力系数[8-10],在大落压比下优势更为明显,当1维等熵控制的面积比达到极限2时,由控制方法得到的推力系数减小速度放慢,这是因喷管出口不再变化造成的。在不同A8下,最优面积曲线有所不同,随落压比的增大,大A8下喷管能达到的最大推力系数减小速度加快。
4 结论
(1)在1个给定的发动机状态下都对应1个最优面积比,在这个面积比上有最大推力系数,最优面积比略小于使喷管燃气完全膨胀的面积比。
(2)最优面积比的影响参数有喷管可用落压比π、燃气总温 T*、A8面积、k、R。其中对最优面积比 Ar影响较大的是π和A8,其它因素对最优面积比的影响不大。
(3)采用1维等熵公式计算面积比的可调收扩喷管推力系数明显小于最高推力系数,且落压比π越大差距越明显。
[1]刘大响,叶培梁.航空发动机设计手册:第7册[M].北京:航空工业出版社,2000:231-233.
LIU Daxiang,Ye Peiliang.Aircraft engine design manual:seventh volumes[M].Beijing:Aviation Industry Press,2000:231-233.(in Chinese)
[2]黄宏艳,王强.过膨胀状态下轴对称收-扩喷管内外流场计算及分析[J].航空动力学报,2007,22(7):1069-1073.
HUANG Hongyan,WANG Qiang.Numerical investigation on internal and external flows for axisymmetric convergentdivergent nozzles on over-expansion state[J].Jouranl of Aerospace Power,2007,22(7):1069-1073.(in Chinese)
[3]胡海洋,王强.跨声速条件下轴对称收扩喷管内外流场的数值研究[J].航空动力学报,2008,23(6):1042-1043.
HU Haiyang,WANG Qiang.Numerical study on combination flow field of axisymmetric convergent-divergent nozzle under transonic and supersonic conditions[J].Jouranl of Aerospace Power,2008,23(6):1042-1043.
[4]索苏诺夫B A,切普金B M.航空发动机和动力装置的原理、计算及设计[M].莫斯科:莫斯科国立航空学院,2003:129-131.
СосуновB A,Чепкин B M.The theory of aero-engine and powerplant[M].Moscow:Moscow State Aviation Institute,2003:129-131.
[5]Frank K L,Douglas A T.Performance analysis of STOVL aircraftnozzle in hover[C]//Las Vegas:41staerospace sciences meeting and exhibit,2003.
[6]George T C,Francis J C.Aeropropulsive characteristics of nonaxisymmetric-nozzle thrust reversers at Mach numbers from 0 to 1.20[R].NASA-TP-2306,1984:13-14.
[7]Atlanta,Georgia.Vectoring exhaust nozzle technology[C]//Los Angeles:AIAA/SAE/ASME 20th joint propulsion conference,1984.
[8]David M,Nick H,Ephraim G.Forward flight effects on the shock structure from a chevron C-D nozzle[R].AIAA-2010-473:230-231.
[9]Eric G,Dwain Terrell PE,Rich D.Nozzle selection and design criteria[C]//Florida:40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit,2004.
[10]金捷,赵景芸,张明恒,等.轴对称矢量喷管内流特性的模型试验[J].推进技术,2005,26(4):145-146.
JIN Jie,ZHAO Jingyun,ZHANG Mingheng,et al.Experimental investigation of static internal performance for an axisymmetric vectoring thrust nozzle[J].Journal of Propulsion Technolgy,2005,26(4):145-146.
