基于核磁共振T2谱三组分分解的致密砂岩储层孔隙结构研究

丛云海，范宜仁，邓少贵，叶绮，陈芳

(1.中国石油大学地球科学与技术学院，山东青岛 266580;2.中国石油大学CNPC测井重点实验室，山东青岛 266580;3.中国石油西部钻探工程有限公司测井公司，新疆克拉玛依 834000)

0 引言

孔隙结构是表征储层储渗性能的重要参数，特别是对于致密砂岩(广义上孔隙度小于10%，渗透率低于1 ×10-3μm2)［1］，其储渗机理复杂，孔隙结构研究已成为该类储层评价的重点及难点所在［2］。长期以来，储层的孔隙结构研究多基于毛细管压力曲线，但对于致密砂岩，单一基于毛细管压力的孔隙结构评价不能很好地表征其微观特征。核磁共振作为储层孔隙结构研究的有效手段之一被广泛应用［3-4］。通常采用的研究方法是将核磁共振T2谱转化为毛细管压力曲线，从而进行孔隙结构评价［5-10］，但此类处理方法往往忽略了T2谱本身所包含的信息(谱形态、幅度等)。刘堂晏、周灿灿等［11-12］利用球管模型对核磁共振T2谱进行分解，研究了不同类型孔隙弛豫特征与孔喉渗流特性，但其分解过程十分复杂，不利于进行快速有效的孔隙结构分析。

本文以实验为依托，选取苏里格气田致密砂岩岩样进行核磁共振T2谱测量与压汞毛细管压力曲线测试，寻找T2弛豫时间与平均孔喉半径的关系，并以平均孔喉半径为桥梁，通过建立核磁共振孔隙结构模型，对核磁共振T2谱进行了三组分分解，得到了岩石中不同形态孔隙的T2谱贡献值，为利用核磁共振T2谱表征致密砂岩渗流能力提供了一种有效的评价方法。

1 核磁共振T2谱与平均孔喉半径的相互关系

根据毛细管压力理论与核磁共振机理，毛细管压力曲线与核磁共振T2谱存在着一定的转换关系，何雨丹等［13］在研究中发现了毛细管压力与T2谱的幂指数关系为

式中，pc为毛细管压力;m、n为系数。根据毛细管压力原理［14］，有

式中，σ为两相界面张力;θ为接触角;r为平均孔喉半径。因此，可以确定T2弛豫时间与平均孔喉半径的幂指数关系为

式中，c、q为转换系数。

为了确定致密砂岩T2-r的转换系数，选取了苏里格地区3种不同特征的致密砂岩进行系统分析，其基本参数信息见表1。

岩样Ⅰ、Ⅱ、Ⅲ是反映致密砂岩孔隙结构的典型样品。图1是其饱和水的T2谱分布，从该谱图中可以看出3块岩样孔隙结构差别较大，其中Ⅰ号样的T2弛豫分布为0.4～300 ms，Ⅱ号样的T2弛豫分布为0.1 ～20 ms，Ⅲ号样的 T2弛豫分布为 0.7 ～300 ms。图2是相同样品的压汞进汞量与平均孔喉半径的关系图。对比图1与图2可以看出，各样品的进汞量形态与T2谱的形态存在一定的相似性，在Ⅰ号样、Ⅲ号样的T2谱与进汞量谱图样均出现了双峰形态;而Ⅱ号样的T2谱与进汞量谱图均出现了单峰特征，由此可以确定核磁共振T2谱与平均孔喉半径存在一定的相关关系，并且T2谱本身可以一定程度地表征孔喉的连通性特征。

比对图1、图2所示的T2谱形态特征与进汞量特征，结合式(3)，将相同样品的核磁共振T2弛豫时间与平均孔喉半径按分布范围及谱型峰谷位置进行等效刻度(见图3)。结果显示T2与r之间存在较好的幂指数关系，同时，可以看出多峰孔隙结构类型的岩样T2-r关系存在分段性。由此得到了不同样品的T2-r转换系数。基于上述分析，确定了通过进汞量特征确定T2-r关系的方法。

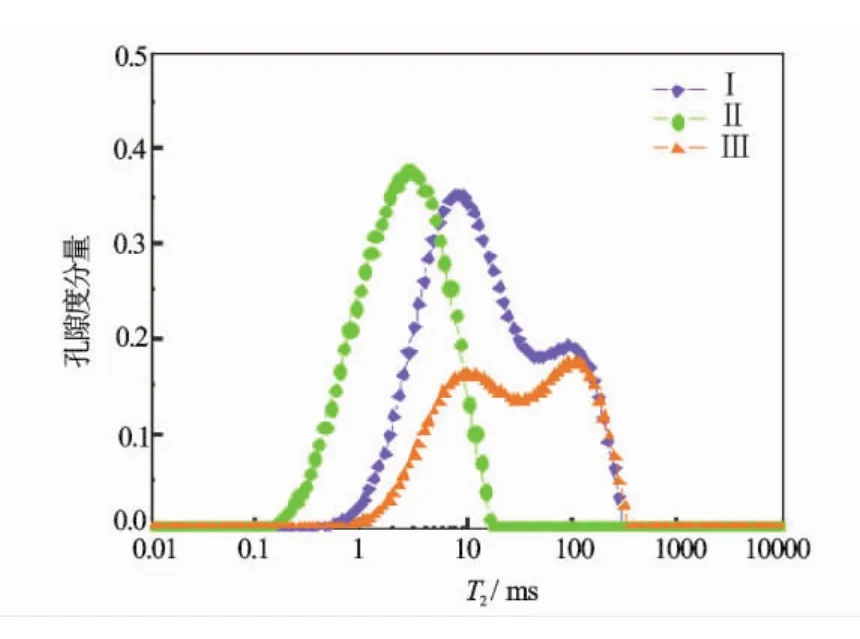
图1 饱和水致密砂岩岩样的T2谱分布

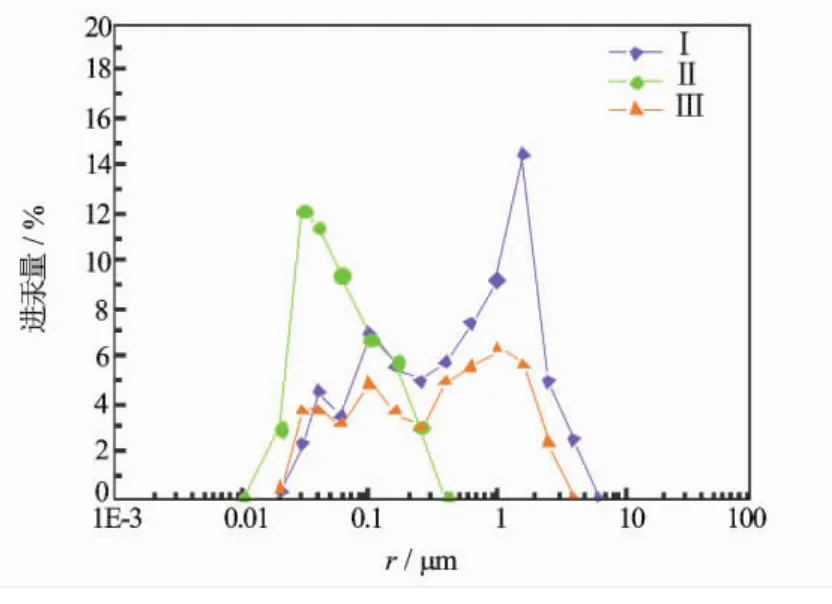
图2 岩样压汞进汞量与平均孔喉半径的关系

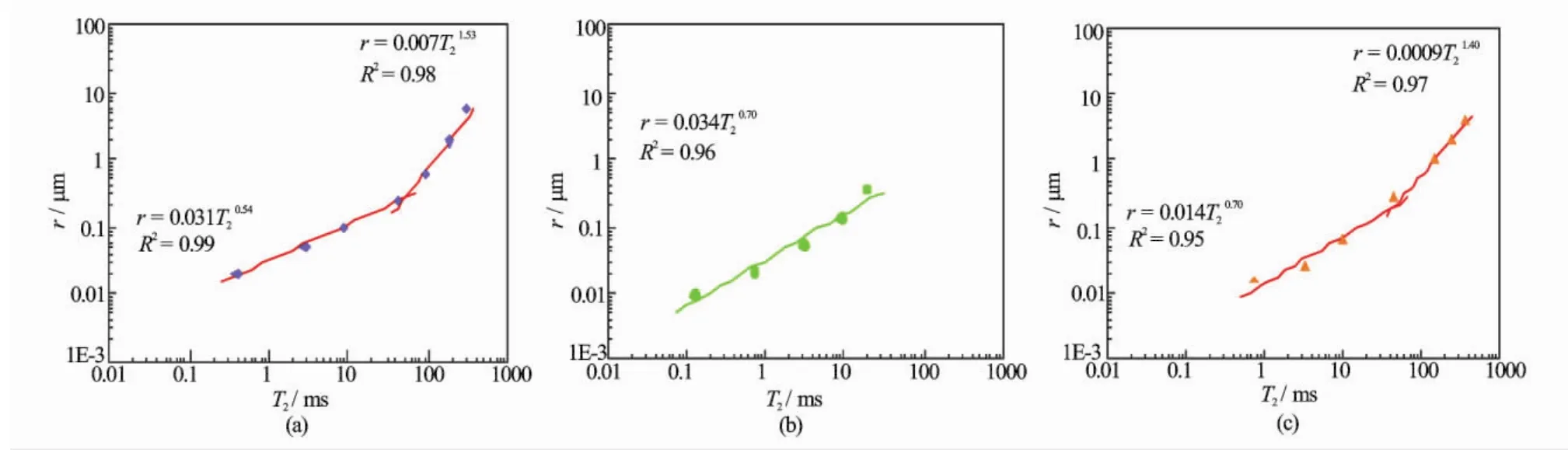
图3 不同样品的T2弛豫时间与平均孔喉半径的转换关系

2 致密砂岩储层核磁共振孔隙结构模型

孔隙介质的横向弛豫T2主要与表面弛豫有关，在表面弛豫中，孔隙起着决定性的作用。弛豫的速度与表面的碰撞率有关，比表面决定了孔隙介质的T2弛豫时间［15］，用公式表示为

式中，S/V为孔隙的比表面积;ρ为表面弛豫率(特定的岩石表面弛豫率为常数)。

孔隙的比表面是平均孔喉半径的函数，令fs为孔隙的形状因子，有

不同形态孔隙空间的形状因子fs存在较大差异，因此，将岩石的孔隙空间等效为球型孔隙、管型孔隙以及槽型孔隙，并认为球型孔隙是孤立的孔隙空间，管型孔隙多为喉道与毛细管孔隙空间，槽型孔隙多为连片的溶蚀空间及裂缝(见图4)等。后两者的模型示意见图5。

根据孔隙结构模型，球型孔隙、管型孔隙与槽型孔隙的比表面积分别由式(6)至式(8)表示

图4 具有槽型孔隙的岩石孔隙空间照片

由此，球型孔隙、管型孔隙与槽型孔隙的孔隙的形状因子 fs分别为:fs球=3;fs管=2;fs槽=1。致密砂岩复杂的孔隙结构则可以用球型、管型与槽型孔隙的加权组合进行等效。

图5 孔隙结构模型示意

3 孔隙结构三组分分解理论的建立

根据等效的孔隙结构模型，认为致密砂岩的孔隙由球型、管型与槽型孔隙共同构成，不同的组合关系反映着岩石的不同流动形态，其关系直接制约着致密砂岩孔隙结构的评价。为了系统表征各孔隙组分在岩石孔隙空间中的分布形式，精细揭示致密砂岩的储渗机理，将核磁共振T2谱按球型、管型与槽型3种孔隙形态进行分解。

由式(3)及基于进汞量分布特征的T2-r关系可知，岩石的孔喉半径与岩石的T2弛豫时间存在幂指数函数关系，即把等效孔喉半径re看做是关于T2的函数，即

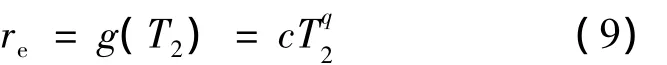
根据半径相等原则，在固定的T2时间上的孔隙信号即为不同组分等效半径的加权平均，令

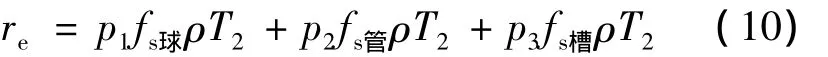
式中，pi为等效加权因子，i=1，2，3分别对应球型、管型、槽型孔隙。

由式(9)、式(10)，以孔喉半径为桥梁建立T2恒等式，即

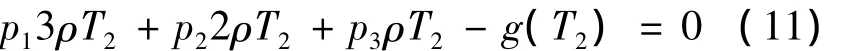
于是问题转化为求解式(11)的系数pi，即求解对给定T2时间下的p1、p2、p3的相对比值，将分解过程转换为数值求解。由于方程为三元欠定方程，解不是唯一，为了最佳地表征致密砂岩的孔隙特征，建立如下假设:

(1)等效加权因子pi的取值范围为(0，1)。

(2)致密砂岩渗透性能的主要贡献来源于连通性最好的槽型孔隙(主要体现在连片溶蚀的孔隙空间及微裂缝等)，认为球型孔隙是孤立的或者连通性差的原生孔隙。

令pi从0.01开始计算，根据误差最小求解原则，通过最优化算法［16］寻找最小pi值下的等效加权因子比例，此时的解即为岩石最大渗透率贡献的三组分分解。该分解最大程度地表征了储集空间的连通性能。通过分解，可以得到不同孔隙结构类型的T2特征谱。

4 分解效果及分析

图6 不同样品的孔隙结构三组分分解

图6是利用孔隙结构三组分分解原理对表1所示岩样进行分解的结果。由于选取岩样的主要连通孔隙空间为溶蚀孔隙，因此对表征孤立的、连通性差的球型孔隙压制效果较好。对于Ⅰ号样品，孔隙空间最大，渗透性能最好，分解后槽型孔隙空间占主体［见图6(a)］;II号样品虽然孔隙储集空间较大，但渗透性极差，渗透率仅为0.06×10-3μm2，分解后可以看到该样品中主要为管型孔隙空间［见图6(b)］，即该岩石的孔隙以微毛细管孔隙为主，属于储集性与连通性均差的孔隙类型;Ⅲ号样品类似Ⅰ号样品，T2谱具有双峰结构，分解后的结构同样以槽型孔隙为主，其渗透性能较Ⅰ号差的主要原因是岩性细、总的储集空间小。

同时，对比图2可以看出，Ⅰ、Ⅲ的2块样品在0.03～0.08μm大小孔隙半径处进汞量明显有下降趋势，说明该半径范围内的孔隙连通性差、毛细管压力高，该现象在分解后的T2弛豫时间2～6 ms明显体现出来。由分解结果可知，处于大孔隙与小孔隙过渡区的中等大小孔隙多发育管型孔隙结构。对分解的结果可做如下解释:

(1)致密砂岩T2谱双峰类型大孔隙部分以强溶蚀作用形成的粒间-粒内复合型溶孔为主，溶蚀现象严重，溶蚀空间连片或成网状，应以槽型孔隙为主。

(2)致密砂岩T2谱双峰类型小孔隙部分，主要为石英颗粒线接触下微弱溶蚀作用所致，储集空间呈板状，孔隙类型同样以槽型孔隙为主。

(3)致密砂岩T2谱单峰形态的孔隙主要以管型孔隙为主，形成管型孔隙的原因是苏里格致密砂岩岩屑含量与泥质含量高，充填堵塞有效储集空间，这种孔隙含有较高的束缚水，增加了孔隙的毛细管压力，对烃类的储集和运移起着极大的抑制作用。

5 结论

(1)压汞进汞量分布可以在一定程度上反映岩石孔隙的连通性，其分布特征与核磁共振T2谱具有相似性，按形态特征刻度可以得到T2-r的转换关系，并且通过理论推导确定其为幂指数关系。

(2)将岩石的孔隙空间等效为球型、管型及槽型的组合可以有效反映岩石的连通性，对于致密砂岩，连通性好的孔隙槽型孔占优，连通性差的孔隙管型孔占优。

(3)具有T2谱双峰形态的岩石以槽型孔隙占优，连通性较好;具有T2谱单峰形态的岩石以管型孔隙占优，孔隙空间以束缚孔隙为主。

(4)孔隙结构三组分分解可以有效揭示岩石孔隙空间各类型孔隙的存在比例和分布形式，分解结果有助于储层有效储集空间的寻找与致密储层孔隙结构的精细评价。

［1］ 戴金星，倪云燕，吴小奇.中国致密砂岩气及在勘探开发上的重要意义［J］.石油勘探与开发，2012，39(3):257-264.

［2］ 中国石油勘探与生产分公司.低孔低渗油气藏测井评价技术及应用［M］.北京:石油工业出版，2009:31-67.

［3］ 肖立志.核磁共振成像测井与岩石核磁共振及其应用［M］.北京:科学出版社，1998:3-44.

［4］ 邓克俊.核磁共振测井理论及应用［M］.东营:中国石油大学出版社，2010:42-75.

［5］ Yakov V，Win L S.A Practical Approach to Obtain Primary Drainage Capillary Pressure Curves from NMR Core and Log Data［J］.Petrophysics，2001，42(4):334-343.

［6］ 运华云，赵文杰，刘兵开，等.利用T2分布进行岩石孔隙结构研究［J］.测井技术，2002，26(1):18-21.

［7］ 何雨丹，毛志强，肖立志，等.核磁共振T2分布评价岩石孔径分布的改进方法［J］.地球物理学报，2005，48(2):373-378.

［8］ 刘堂宴，傅容珊.核磁共振谱的岩石孔喉结构分析［J］.石油地球物理勘探，2003，38(3):328-333.

［9］ 邵维志，丁娱娇，刘亚，等.核磁共振测井在储层孔隙结构评价中的应用［J］.测井技术，2009，33(1):52-56.

［10］李天降，李子丰，赵彦超，等.核磁共振与压汞法的孔隙结构一致性研究［J］.天然气工业，2006，26(10):57-59.

［11］刘堂晏，肖立志，傅容珊，等.球管孔隙模型的核磁共振(NMR)弛豫特征及应用［J］.地球物理学报，2004，47(4):663-671.

［12］周灿灿，刘堂晏，马在田，等.应用球管模型评价岩石孔隙结构［J］.石油学报，2006，27(1):92-96.

［13］何雨丹，毛志强，肖立志，等.利用核磁共振T2分布构造毛细管压力曲线的新方法［J］.吉林大学学报:地球科学版，2005，35(2):177-181.

［14］秦积顺，李爱芬.油层物理学［M］.东营:中国石油大学出版社，2006:211-218.

［15］王树寅，李晓光，石强，等.复杂储层测井评价原理和方法［M］.北京:石油工业出版社，2006:117-121.

［16］唐焕文，秦学志.实用最优化方法［M］.大连:大连理工大学出版社，1994.