微控制器射频抗扰性与受测引脚类型的关系

粟 涛 杨叶花 王自鑫 陈弟虎

(中山大学物理科学与工程技术学院，广东 广州 510275)

引 言

随着电磁环境日益恶劣，现代电子系统遭受严重的电磁干扰[1-2].一种重要的干扰就是射频波段的干扰.国际标准机构已经为射频波段的干扰制订了针对机电系统和电路板的电磁抗扰性测试标准.现代电子系统以集成电路为核心成份，它的抗扰性是整个电子系统抗扰性的关键.因此，有必要对集成电路的电磁抗扰性进行单独表征.在工业界需求的推动下，国际电工委员会(International Electrotechnical Commission,IEC)开始建立专门用于集成电路射频电磁抗扰性(以下简称为抗扰性)的测试标准[3].目前的测试标准草案仅仅给出了测试框架，很多具体设置还有待确定.

微处理器、微控制器和系统芯片属于复杂集成电路.一方面，它们被广泛地应用于安全、运输、通信、娱乐、工业控制，其影响领域广.另一方面，它具有多个模块、多个引脚，其物理结构复杂.此外，这些复杂集成电路也是电路系统里最重要和最昂贵的器件.研究复杂集成电路的抗扰性具有很强的实用背景和学术价值.

器件和模块级的集成电路在功能和结构上都比较简单，对这些电路进行抗扰性测试，其方法比较简单,测试时间也短.复杂集成电路往往有上百的引脚，并且其运行状态也可重构.要完整的表征复杂集成电路的抗扰性，让测试结果有对比性，还要满足时间和人力的限制，这就使得测试标准的制订面临很多技术难题.这些技术难题中的两个重要问题是待测引脚的选择问题和根据测试结果对抗扰性进行定级的问题.

对集成电路射频抗扰性的研究开始于20世纪70年代[4].对微控制器这类复杂集成电路的抗扰性的研究开始于20世纪90年代末.研究内容[5-10]包括表征、测试电路板设计和建模仿真.然而，目前为止的研究还未能解决上面两个问题.

针对所存在的问题，本文认为，要解决第一个问题必须先理解抗扰性和受测引脚之间的关系，然后根据这个关系来确定需要测试的引脚.而抗扰性与受测引脚的关系首先是抗扰性与受测引脚类型的关系.要解决第二个问题，首先必须将微控制器的引脚分类，因为同类引脚的测试结果才有可比性；然后，对每一类引脚的抗扰性给出一个特征值，再根据这个特征值的范围来进行定级.因此，本文的研究目的，一是找到微控制器抗扰性和受测引脚类型的关系，二是为每个类型的受测引脚给出一个能用来进行抗扰性定级的特征值.

以微控制器为例来研究复杂集成电路的抗扰性.微控制器的引脚按照其功能可分为三类：数据输入输出引脚(以下简称为数据引脚)、电源引脚和晶振引脚.本文分析这三类受测引脚的抗扰性.为使分析结果具有一般性，也为了获得某类受测引脚的抗扰性共性，需要对多款微控制器进行测试和比较.本文选取英飞凌科技公司四个型号的微控制器TC161(DUT-1)、XC161(DUT-2)、XC2287(DUT-3)和TC1767(DUT-4)进行测量.这些微控制器隶属于前后四代.它们的制造工艺、功能和配置都不一样.通过对这些微控制器的分析，可以获得同类型引脚抗扰性的基本共性.

1 测量方法及抗扰性的定义

本文采用国际电工技术委员会测量标准(IEC 62132-4)[11]中描述的直接功率注入(Direct Power Injection,DPI)方法进行抗扰性测量.测量装置如图1所示.受测器件安装在特制的测试板上，其内部运行一个监视程序，这个程序会选择微控制器上的一个引脚输出一个反馈信号，来表明微控制器的运行状态.有关监视程序的详细介绍可参见文献[12].单一频率的正弦射频杂波(以下简称为杂波)由信号发生器合成后经功率放大器产生，通过一个定向耦合器和一个电容注入到受测引脚.定向耦合器还用于测量杂波的正向功率和反向功率.

图1 实验装置

在图1的计算机里运行的测试程序如图2所示.在测试过程中，连续增大杂波的输出振幅，直到微控制器发生错误或正向功率达到一个上限值，此时的正向功率就被作为该频率下该引脚曲线的抗扰度.改变杂波的频率进行重复试验，可得到整个射频范围内的抗扰度.我们对0.5 MHz～1.0 GHz范围内的干扰信号进行测量，每个频率的杂波强度上限值为37 dBm.将信号源、放大器和定向耦合器所组成的电路称为干扰源，干扰源的内阻为RS= 50 Ω.本文将频率分成三段:小于0.5 MHz称为低频段；0.5～50 MHz称为中频段；大于50 MHz称为高频段.在高频段，微控制器的抗扰性受封装及印刷电路板(Printed Circuit Board,PCB)的寄生元素的严重影响，它的失效机理相当复杂[12].本文主要研究中频段杂波信号注入微控制器的抗扰性.

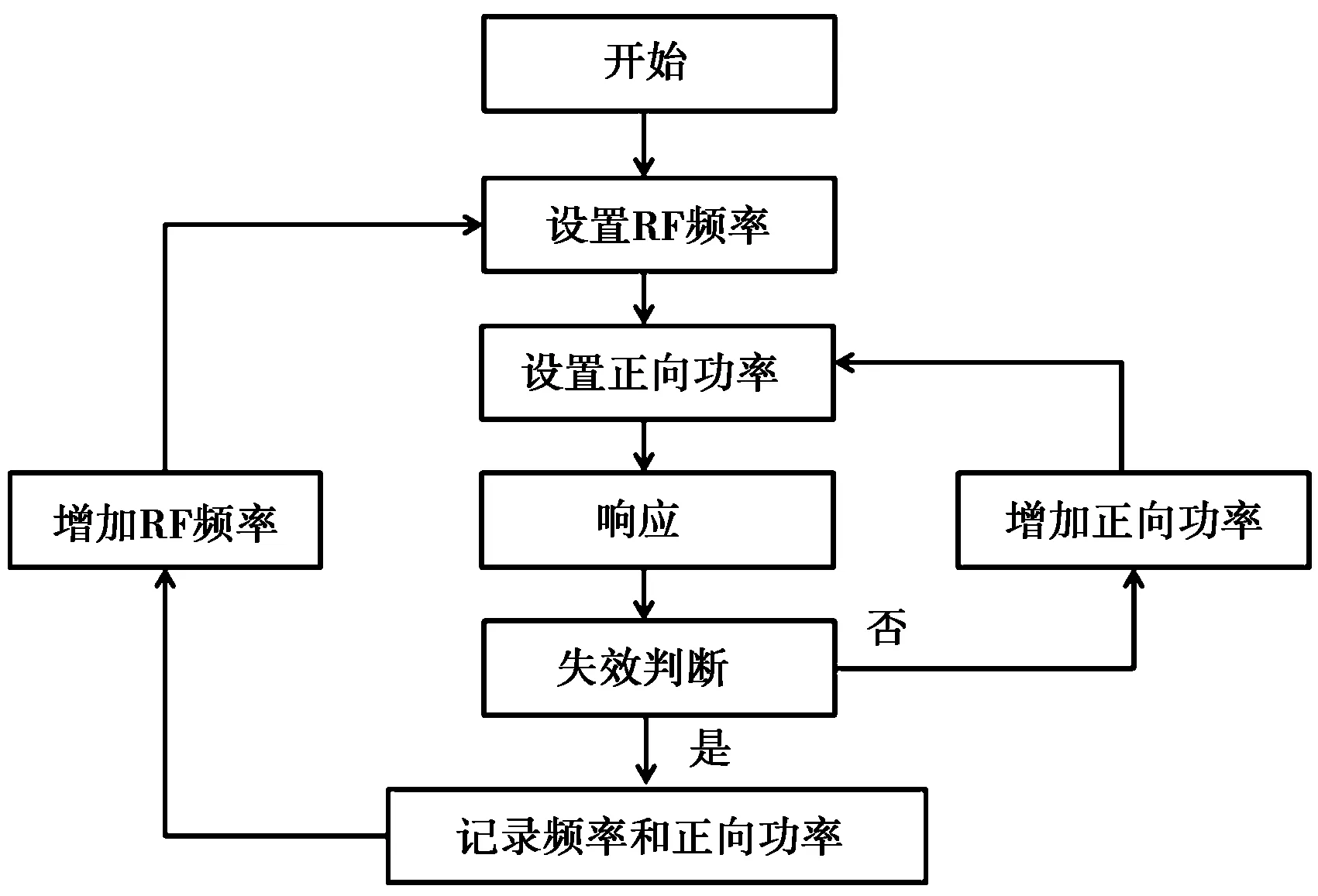
图2 测试步骤原理图

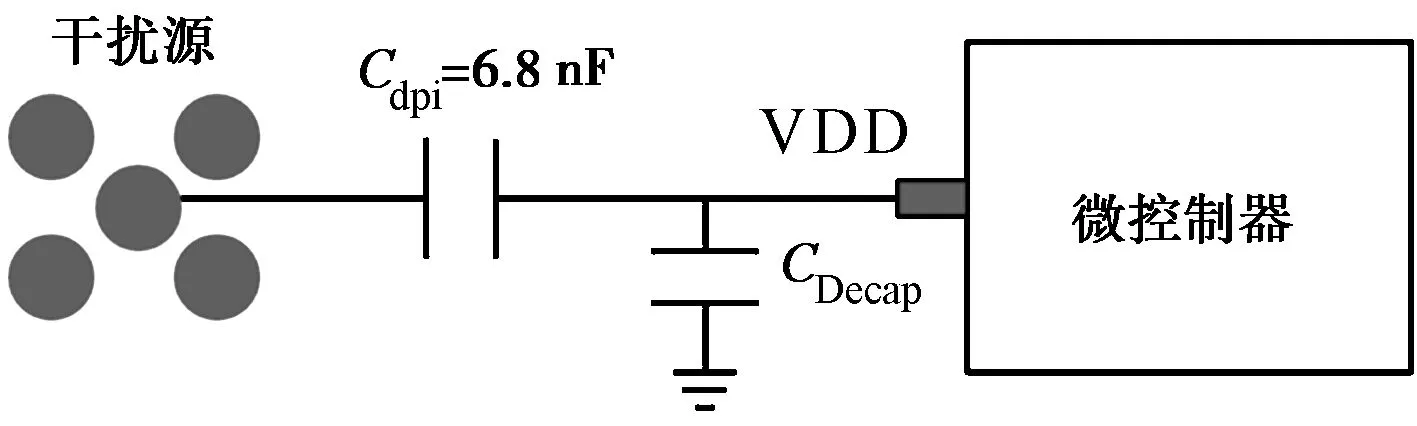
对微控制器数据引脚、电源引脚和晶振引脚进行实验时，杂波注入受测引脚的方式及负载方式都不一样，如图3所示.

(a) 数据引脚

(b) 电源引脚

(c) 晶振引脚图3 杂波信号注入不同引脚时的连线图

对数据引脚进行抗扰性测量时，总是将相邻的两个数据引脚相连，其中一个引脚作为输出引脚(Data Output,DO)，另一个引脚作为输入引脚(Data Input,DI).DI读取来自DO的信号并判断它的逻辑电压.杂波通过一个注入电容耦合到DI.如果DI读取的逻辑电压与DO注入的逻辑电压不一致，数据引脚功能被认为出错，微控制器内的监视程序会产生报错的反馈信号，使测试计算机判定微控制器失效.注入电容的大小为6.8 nF，这样的注入电容，既保证干扰信号在所测频段内能从干扰源充分耦合到受测引脚，又能保证数据引脚在高低电平间翻转时无需太长的过渡时间.

对电源引脚进行抗扰性测量时，跟注入数据引脚一样，杂波通过注入电容耦合到电源引脚.电源引脚上同时还接有去耦电容.去耦电容一般在10 nF至1 μF的量级.选用大小为6.8 nF的注入电容不会对电路的上电和噪声行为造成明显影响.

每个晶振引脚有一个负载电容，两个引脚之间是晶振.晶振输出引脚(XTAL2)驱动电流比较小，过大的注入电容会破坏起振.对晶振输入(XTAL1)的注入电容值应接近和低于负载电容，本文选取值为4.7 pF的电容.在测试时，微控制器会自动检测竞争产生的时钟信号.

研究抗扰性时，每次只往一个引脚注入杂波.多个引脚同时注入杂波，不但会同时干扰多个电路模块，还会在同一模块处出现杂波的叠加.这种情况更为复杂，可作为未来的工作单独研究.

2 理论分析

不同微控制器的引脚数目不同，但这些引脚大致可分为3类：数据引脚、电源引脚和晶振引脚.同一块微控制器不同类型引脚的抗扰性也不同,这一方面是因为不同类型引脚的阈值电压不同，另一方面是因为经过不同类型引脚，杂波从干扰源到焊盘(处于芯片上，下同)的传输系数不同.要使微控制器正常工作，必须满足

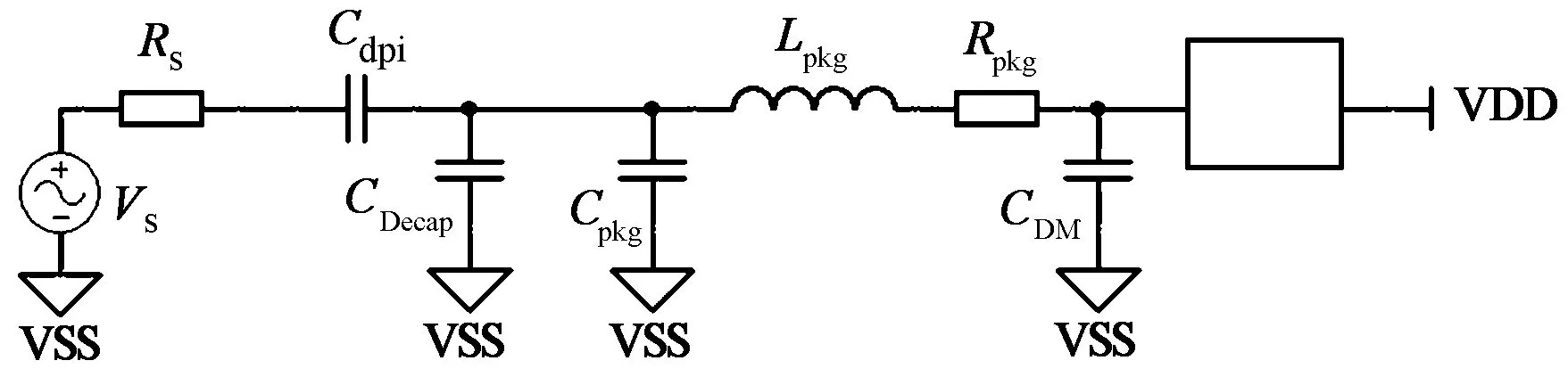
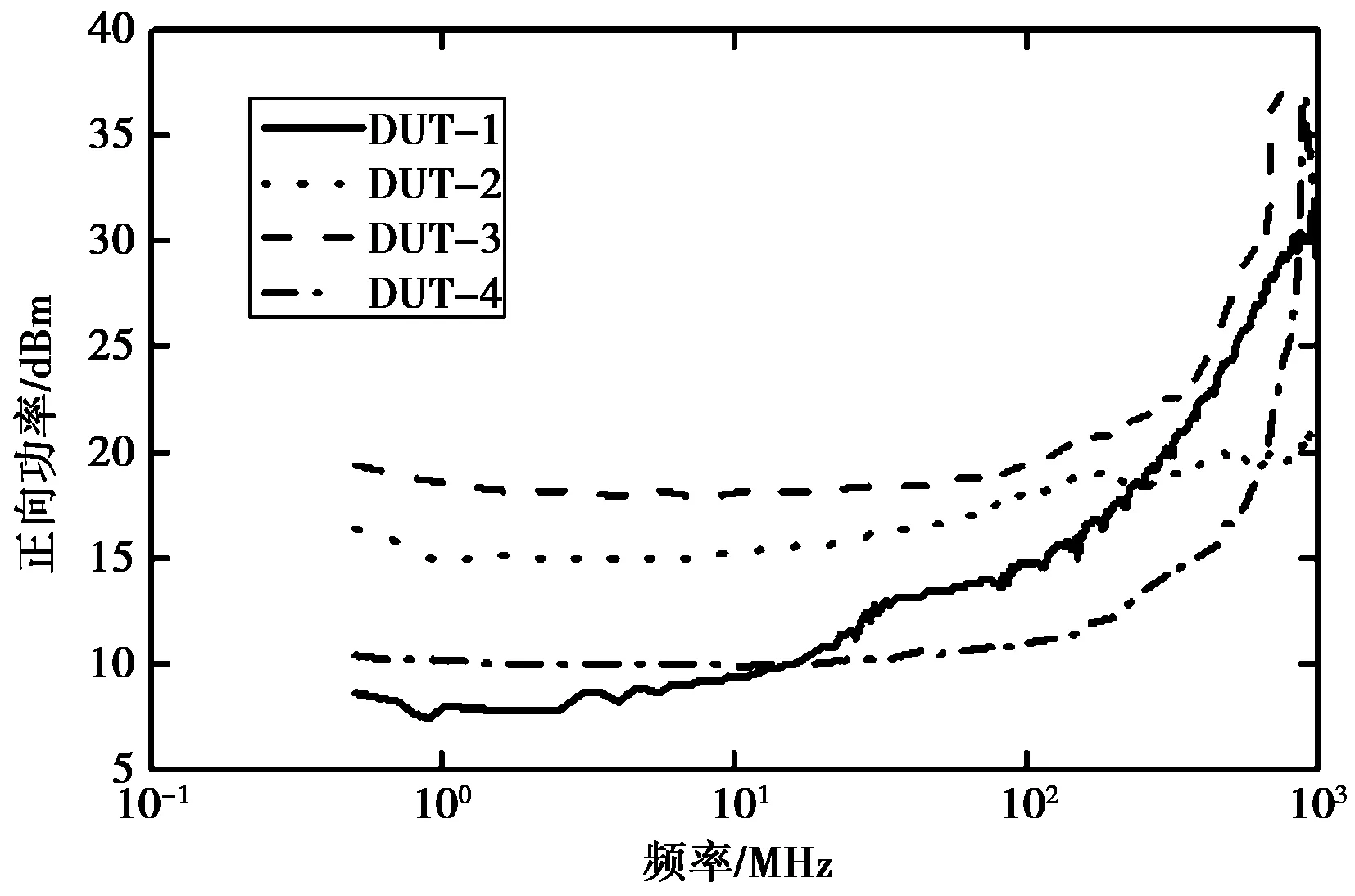
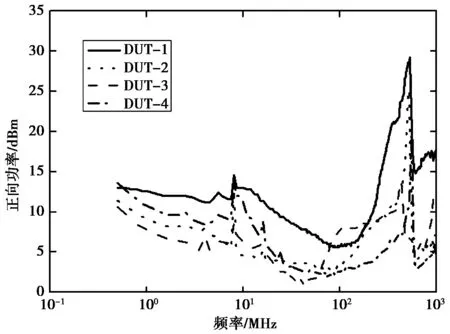
Vpad

(1)

式中：Vpad为引脚焊盘上电压；Vth为焊盘所连接功能模块能够承受的最大杂波电压.不同类型引脚所连接的功能模块不同，所以阈值电压Vth也会不同.因此，Vth是决定不同类型引脚抗扰性的重要参数.

传输系数通过下式计算：

(2)

式中：α为传输系数，其值取决于传输路径；VS为干扰源.传输路径指的是干扰信号通过注入电容、封装，最后注入引脚焊盘的路径.由于路径中的注入电容、电路板走线还有芯片封装，它们的阻抗有很强的频率依赖性，所以α由传输路径和干扰信号频率共同决定.

结合式(1)、(2)，有

(3)

式中VSth为微控制器能够承受的最大干扰源电压.将源电压换算杂波的正向功率，以毫瓦为单位，有

(4)

式中PSth为抗扰度.式(4)是估算引脚抗扰度的一般性公式，式中的Vth和α是与器件工艺、器件电路和器件引脚类型有关的参数.

2.1 数据引脚的抗扰性特征值

分析杂波信号从数据引脚注入微控制器的抗扰性模型如图4所示.VS为杂波信号源，RS为干扰源的内阻，Cdpi为注入电容，Lpkg、Rpkg、Cpkg分别为封装的寄生电感、寄生电阻和寄生电容，Cpad_DI_VDD、Cpad_DI_VSS、Cpad_DO_VDD、Cpad_DO_VSS分别为数据输入焊盘、数据输出焊盘与电源端、接地端的耦合电容，RP为上拉电阻，而RN为下拉电阻.部分元器件的取值范围如表1所示，可见Cpkg很小，在实验测试的频率范围内，阻抗非常大，而Lpkg的阻抗在测试的频率范围内很小，Rpkg也很小，它们在整个测试过程中可以近似为导线，通过Cdpi的杂波信号几乎全部注入到引脚焊盘上.所以，数据引脚的传输路径的特性主要由Cdpi和RP(或RN)决定.

图4 分析杂波信号从数据引脚注入微控制器的抗扰性模型

RSCdpiCpkgLpkgRpkg50Ω6.8nF～1pF1～5nH1Ω

结合图4，并考虑到封装寄生参数的取值范围，可知在中频范围内，输入引脚焊盘的电压与输出引脚焊盘上的电压基本相等.输出高电平(数位1)时，有

(5)

式中：

(6)

αDIO_H为杂波信号注入数据引脚并输出高电平时的传输系数；RP为上拉电阻；RN为下拉电阻；ωc为截止频率，通常ωc远远小于中频段杂波信号的ω.在中频段αDIO_H随频率增大缓慢增大，甚至几乎不变,αDIO_H化简为

(7)

相应地，输出低电平(数位0)时，只需将上RP替换成RN，所以有

(8)

式中αDIO为杂波信号注入数据引脚的传输系数.

(9)

式中：Vth_DIO为数据引脚焊盘上杂波的阈值电压;Vth_1→0为输入电压由高电平向低电平转换的参考电压；Vth_0→1为输入电压由低电平向高电平转换的参考电压.数据引脚的输入引脚在判断电压的数位时会将其和数位转换参考电压相比较.当且仅当杂波幅度小于Vth_DIO，输入引脚探测到的实际数位与输入引脚输出的数位一致.

结合式(4)有

20lg|>αDIO|输出高/低电平}.

(10)

式(10)就是数据引脚抗扰度公式.从式(8)、(9)和(10)可知，端口电压、正向阈值电压、反向阈值电压、驱动电阻和杂波源内阻是决定数据引脚抗扰力的关键因素.此类引脚在中频波段的抗扰度随频率增大缓慢减弱到最小值，然后基本不变.

需要说明的是，注入数据引脚的杂波可能会进入微控制器芯片上的其他模块，造成其他模块失效.在中低频段，杂波需要首先进入电源分配网络然后进入其它模块.因为电源分配网路上有较多的去耦电容数据，引脚通道也有较大阻抗，所以上述到其他模块的路径传输系数会比较小.要导致其他模块失效，需要远大于导致数据引脚功能失效的杂波强度.这条路径的影响可不考虑.高频传输路径的确会造成其他模块先失效，但这不是本文的关注频段.对于高频路径影响的分析可参见文献[12].另外，数据引脚功能失效后会导致其他模块功能的失效，但无论如何微控制器的抗扰性仍由数据引脚功能决定.因此，本小节和以下各节都不考虑微控制器各模块间的相互作用.

2.2 电源引脚的抗扰性特征值

分析杂波信号从电源引脚注入微控制器的抗扰性模型如图5所示.VS为干扰源，Rs为干扰源的内阻，Cdpi为注入电容，Lpkg、Rpkg、Cpkg分别为封装的寄生电感、寄生电阻和寄生电容，CDecap为PCB板上的去耦电容，CDM为电源引脚焊盘与接地端间的片上去耦和片上寄生电容，称为芯片域电容.

干扰信号通过Cdpi注入到电源引脚时，一部分信号通过CDecap直接耦合到PCB接地端，一部分通过封装直接耦合到PCB接地端或传输到电源引脚焊盘再耦合到PCB接地端.而每个电源引脚焊盘存在一个阈值电压，当电源引脚上的电压超过它的阈值电压时，电源引脚功能出错或损坏，干扰信号的这个临界功率值即为该频率下电源引脚的抗扰度.

图5 分析杂波信号从电源引脚注入微控制器的抗扰性模型

同分析数据引脚抗扰力时一样，在分析电源引脚在低频和中频范围内的抗扰力时，Cpkg、Lpkg和Rpkg的影响很小可忽略，则电源引脚焊盘上的电压几乎等于电源引脚上的电压，有

(11)

式中：αsply为杂波信号注入电源引脚的传输系数；ωc为截止频率；RS为50 Ω；CDecap为 6.8 nF.

ωc由式(12)计算

(12)

αsply呈一阶低通型，而ωc远小于中频波段的ω，因此αsply在中频波段随频率一阶递减，αsply可以化简为：

(13)

结合式(4)可得

(14)

式中Vth_sply为电源引脚正常工作的阈值电压，式(14)就是电源引脚电源引脚抗扰度公式.从式(13)和(14)可知，电源引脚焊盘阈值电压、杂波源内阻、去耦电容和芯片域电容是决定电源引脚抗扰度的关键因素.而从表2里的典型取值来看，去耦电容要远大于芯片域电容，因此去耦电容将主导电源引脚的抗扰度，抗扰度随去耦电容的增大而增强.

表2 图5部分元件数值

2.3 晶振引脚的抗扰性特征值

分析杂波信号从晶振引脚注入微控制器的抗扰性模型图6所示.VS为干扰源，Rs为干扰源的内阻，Cdpi为注入电容，Lpkg、Rpkg、Cpkg分别为封装的寄生电感、寄生电阻和寄生电容，CX1为晶振输入引脚的负载电容，Ccry为晶振的寄生电容，Cpad_X1_VDD、Cpad_X1_VSS分别为晶振输入引脚焊盘与电源端、接地端间的耦合电容.

干扰信号通过Cdpi进入晶振输入引脚时，一部分信号通过CX1耦合到PCB接地端，一部分流经晶振回到PCB接地端，剩下的通过封装耦合到接地端或通过封装传输到引脚焊盘再耦合到PCB接地端.

而晶振焊盘有个阈值电压，当晶振焊盘电压超过这个阈值电压时，晶振引脚功能出错甚至损坏，干扰信号的这个临界功率值即为该频率下晶振引脚的抗扰度.

图6 分析杂波信号从晶振引脚注入微控制器的抗扰性模型

同分析数据引脚、电源引脚抗扰力一样，分析晶振输入引脚在低频和中频范围内的抗扰力时，忽略Cpkg、Lpkg和Rpkg的影响，则晶振输入引脚焊盘上的电压几乎等于晶振引脚上的电压，有

(15)

式中：αX1为杂波信号注入晶振引脚的传输系数；RS为50 Ω；Cdpi为 4.7 pF.

ωc由(15)计算

(16)

αX1呈一阶低通型，而截止频率ωc远大于中频波段的ω，因此传输系数在中频波段近似为常数.αX1化简为

(17)

结合(4)式可得

(18)

式中Vth_X1为晶振引脚正常工作的阈值电压，式(18)就是晶振引脚抗扰度公式.从式(17)和(18)可知，注入电容、负载电容和晶振电容是决定晶振引脚抗扰度的关键因素.此类引脚在中频波段的抗扰度随频率变化不大，接近为常数.从表3里的典型取值来看，各电容对抗扰度的重要性相近.

表3 图6部分元件数值

3 实验测量结果

针对理论分析中提出的各类引脚抗扰度频率特性和特征值，本节通过实际测量的方法来验证其适用性.

3.1 对数据引脚抗扰度公式的验证

对四类微控制器离晶振引脚比较远的数据引脚进行实验，测试结果如图7示.实验结果表明：在中频范围内微控制器数据引脚的抗干扰能力随干扰信号频率的增大而缓慢变化，甚至不变.这与理论分析的结果吻合.

图7 四类微控制器数据引脚的抗扰性

为了验证抗扰度方程的准确性，将四类微控制器数据引脚在3 MHz(对应曲线底部)的测试值与式(10)计算值进行比较，如表4所示.计算抗扰度所用到的Vth_DIO的值是通过实验对低频杂波测定的.原则上,Vth_DIO和后面要用到的各类Vth，都是随频率变化的，不过Vth的频率特性值得单独研究，并且尚在研究之中，因此本文暂且使用低频条件下的Vth来计算抗扰度.

表4 数据引脚抗扰性测试结果和估算值的比较

由表4可见数据引脚抗扰性的测试值和式(10)的计算结果很接近，差异在3.2 dB以内，所以我们可以用公式(10)式来估算微控制器数据引脚的抗扰度.

3.2 对电源引脚抗扰度公式的验证

从式(13)可知传递系数αsply随耦合电容CDecap的增大而减小，结合公式(14)式知，微控制器电源引脚抗扰力随去耦电容CDecap的增大而增强.CDecap位于PCB上，轻易可调.因此可以通过调整去耦电容CDecap值来验证式(14).电源引脚抗扰力的影响，我们对微控制器DUT-2的一个电源引脚分别接0 nF、100 nF、200 nF和300 nF的去耦电容CDecap进行四次试验，实验测试结果如图8所示.实验结果表明：在低频和中频范围内微控制器电源引脚的抗干扰能力随杂波频率的增大按一阶上翻的斜率增强，并且也随去耦电容增大而增强，这与理论分析相一致.高频段抗扰度随频率不升反降，形成孔洞结构，这主要是由电路谐振引起的.对此类结构的详细分析参见文献[12].

图8 DUT-2接不同去耦合电容时电源引脚的抗扰性

为了验证抗扰度方程的准确性，将DUT-2电源引脚在0.5 MHz的测试值与式(14)计算值相比较，如表5所示.计算抗扰度所用到的Vth_sply的值是通过实验对低频杂波测定的.

表5 电源引脚在0.5 MHz的抗扰性

可见电源引脚抗扰性的测试值和式(14)的计算结果很接近，差异在2.5 dB以内，所以我们可以用式(14)来估算微控制器电源引脚的抗扰度.

3.3 对晶振引脚抗扰度公式的验证

对四个型号的微控制器的晶振输入引脚XTAL1进行实验，测试结果如图9所示.实验结果表明：在低频和中频范围内微控制器晶振引脚的抗干扰能力随干扰信号频率的增大而变化，变化幅度要明显比数据引脚的大.这表明作为射频电路的振荡器，它本身具有较明显的本征频率特性.而式(18)仅仅考虑了杂波传输网络的频率特性，没有考虑到电路本征频率特性，因此不能精确的描述出此类引脚抗扰度的频率特性.

图9 四类微控制器晶振引脚的抗扰性

为了进一步确定抗扰度方程的适用性，将四类微控制器晶振引脚在0.8 MHz的测试值与式(18)式计算值进行比较，如表6所示.计算抗扰度所用到的Vth_x1的值是通过实验对低频杂波测定的.

表6 晶振输入引脚抗扰性测试值与估算值的比较

晶振输入引脚抗扰性的测试值和式(18)的计算结果相比，型号DUT-2、 DUT-3、 DUT-4微控制器的差异在3.5 dB以内，而DUT-1的差异为5.9 dB.这种差异要比前面数据引脚和电源引脚的大.重新回到图9，可以看到在低频波段，DUT-4的抗扰度很高.这是因为DUT-4的时钟引脚包含阻碍直流的电路；在高频波段，受测部件抗扰度的顺序变化剧烈；但在0.6～20 MHz 这个振荡放大器的工作波段，四个型微控制器的抗扰度随频率变化较小，并且顺序不变.式(18)对这四个微控制器抗扰度的排序是正确的.综合上面的分析，式(18)只能部分地反应出微控制器晶振引脚的抗扰度频率特性.在振荡放大器工作频率范围内，我们可以用式(18)来对微控制器晶振引脚的抗扰度进行粗糙的估算.

4 结 论

文章将微控制器的引脚分为数据引脚、电源引脚和晶振引脚三类，分别对各类引脚所表现的抗扰性进行分析.文章为每类受测引脚构建了基于杂波传输路径的抗扰性模型，根据这种模型，推导了各类引脚的抗扰度特征值的公式.实验测量值和计算值的对比表明：在中频波段，抗扰度公式能正确地反应出数据引脚和电源引脚的抗扰性，也能一定程度的反应出晶振引脚的抗扰性.对数据引脚和电源引脚，可以选择抗扰度公式所代表的特征值来对不同型号微控制器的抗扰性进行排序和定级，可以用抗扰度公式计算抗扰度，还可以通过调节抗扰度公式各个变量来优化抗扰性.对晶振引脚，在计算抗扰度时还需要考虑到振荡器本身的频率特性，但可用抗扰度公式计算抗扰性的顺序和制订优化方案.特征值的提出，使得不同微控制器的抗扰性有了可比性，只要比较同类引脚抗扰度的特征值就可以判断不同微控制器抗扰性的强弱.特征值计算式的建立，则给抗扰性优化提供了方向.诚然，要对微控制器的总体抗扰性进行较完整的评估还需要研究芯片上不同模块间的高频耦合通道，需研究多个引脚同时受扰的情况，但本文所提出的抗扰性模型和抗扰度公式反应了微控制器抗扰性的基本面，它们是理解、比较和优化微控制器抗扰性的有效工具.

[1] 李 君, 万里兮, 廖 成, 等. 系统级封装新型埋入式电源滤波结构的研究[J]. 电波科学学报, 2009, 24(3): 446-451.

LI Jun, WANG Lixi, LIAO Chen, et al. A novel embedded power filter structure research in system-in-package[J]. Chinese Journal of Radio Science, 2009, 24(3): 446-451.(in Chinese)

[2] 赵勋旺, 张 玉, 梁昌洪. 舰载多天线系统电磁兼容性分析[J]. 电波科学学报, 2008, 23(2): 252-256.

ZHAO Xunwang, ZHANG Yu, LIANG Changhong. Fast EMC analysis of multiple shipborne antennas system[J]. Chinese Journal of Radio Science, 2008, 23(2): 252-256.(in Chinese)

[3] IEC TC/SC 74A (2012) Working Documents [R/OL]. [2012-09-07]http://www.iec.ch, 2012.

[4] RICHARDSON R E, PUGLIELLI V G, AMADORI R A. Microwave interference effect in bipolar transistors[J]. IEEE Transactions on EMC, 1975, 17(4): 216-219.

[5] BAFFREAU S, BENDHIA S, RAMDANI M, et al. Characterisation of microcontroller susceptibility to radio frequency interference[C]// IEEE International Caracas Conference on Devices, Circuits and Systems. Aruba, 2002: 1031.

[6] ICHIKAWA K, INAGAKI M, SAKURAI Y, et al. Simulation of Integrated circuit immunity with LECCS model[C]//17th Annual Zurich Symposium on Electromagnetic Compatibility. Singapore, February 27 2006-March 3, 2006: 308-311.

[7] BOYER A, BENDHIA, SICARD E. Modelling of a direct power injection aggression on a 16 bit microcontroller input buffer[C]//EMC Compo. Turin, 2007: 35-39.

[8] ALAELDINE A, PERDRIAU R, RAMDANI M, et al. A direct power injection model for immunity prediction in integrated circuits[J]. IEEE Transactions on Electromagnetic Compatibility, 2008, 50: 52-62.

[9] WAN F, DUVAL F, CAO H, et al. Increase of immunity of microcontroller to conducted continuous-wave interference by detection method[J]. Electronics Letters, 2010, 46(16): 1113-1114.

[10] GROS J, DUCHAMP G, LECANT J, et al. Control of the electromagnetic compatibility: an issue for IC reliability[J]. Microelectronics Reliability, 2011, 51(9): 1493-1497.

[11] IEC TC/SC 74A. Integrated Circuits Measurement of Electromagnetic Immunity-Part 4: Direct RF Power Injection Method[S]. IEC Standard 62132-4, 2006.

[12] SU T, URGER M, STEINECKE T, et al. Using error-source switching(ESS) concept to analyze the conducted radio frequency electromagnetic immunity of microcontrollers[J]. IEEE Transactions on Electromagnetic Compatibility, 2012, 54(3): 634-645.