不同带宽高功率电磁环境对架空线缆耦合效应分析

孟 鑫 周璧华 曲新波

(解放军理工大学电磁环境效应与光电工程国家重点实验室，江苏 南京 210007)

引 言

国际电工委员会标准IEC 61000-2-13[1]将电场强度超过100 V/m的电磁环境称为高功率电磁环境，主要包括：雷电电磁脉冲(Lightning Electromagnetic Pulse, LEMP)、高空核电磁脉冲(High-Altitude Nuclear Electromagnetic Pulse, HEMP)、高功率微波(High Power Microwave, HPW)和超宽带(Ultra-Wideband,UWB),众所周知，高功率电磁环境对电子、电气设备及系统的安全运行构成严重威胁.随着信息时代的到来，对高功率电磁环境的防护问题越来越重要，正受到人们的广泛重视.值得注意的是，电子、电气设备及系统中用于传输能量与信息的线缆，一旦处于高功率电磁环境中，通过场线耦合会在设备端口上形成过电流、过电压，从而造成系统性能降低以致永久性损伤.因而，分析高功率电磁环境对各类传输线的耦合效应对电子、电力系统的防护有重要意义和应用价值[2-4].

国外早在20世纪60年代就已开展场线耦合问题的研究.其中，E. E. Vance[5]最早提出了运用传输线(TL)模型来分析架空输电线路上的感应电流或感应电压，并给出了架空输电线终端响应的具体求解公式. M. V. Lanoz[6]给出了计算场激励下架空线路响应的格林函数，可方便地用于计算架空输电线任意点处的感应电流、感应电压.另外，J. Beilfuss[7]运用模式传播理论分析了场激励下多导体传输线的响应问题，建立了传输线响应的最大值与传播模式之间的关系，但此方法计算烦琐，并不被常采用.在E．E Vance研究成果的基础上，分析电磁脉冲作用下线缆耦合的TL方法在20世纪70年代和80年代得到广泛应用[8-9]，发展日益成熟.这种方法的优点在于比较简单，但忽略了天线电流即导体的二次辐射，属近似方法.随着计算电磁学的不断发展和计算机运算能力的不断提高，将场线耦合作为电磁散射问题进行时域全波分析已成为可能[10-11].

为分析高功率电磁环境下架空线缆的耦合效应，本文采用并行时域有限差分(FDTD)算法[12]，分别计算了LEMP(IEC 61643-1)、HEMP(贝尔波形)和HEMP(IEC 1000-2-9)三种电磁脉冲作用下架空线缆的外导体感应电流和终端电压.为减小计算机内存和计算时间的需求，采用时域卷积PML截断计算区域；同时，沿线缆轴线方向采用扩展网格.为进一步提高效率，并行算法得以采用，将原始计算区域根据处理器的数量沿线缆轴向进行一维区域分解，每个处理器只需计算问题区域的一部分[13-14]，大大缩短了计算时间.

1 计算模型和方法

1.1 场线耦合模型

电磁脉冲作用下架空线缆耦合模型如图1所示，平行于地面敷设的架空线长为l，距地面高度为h.架空线两端接匹配电阻RL，其下端与接地体相连接，接地体为细长导体，埋深1 m.有耗大地相对介电常数和电导率分别取εrg=10和σg=10-3S/m.电磁脉冲的来波方向由角θ和φ决定.

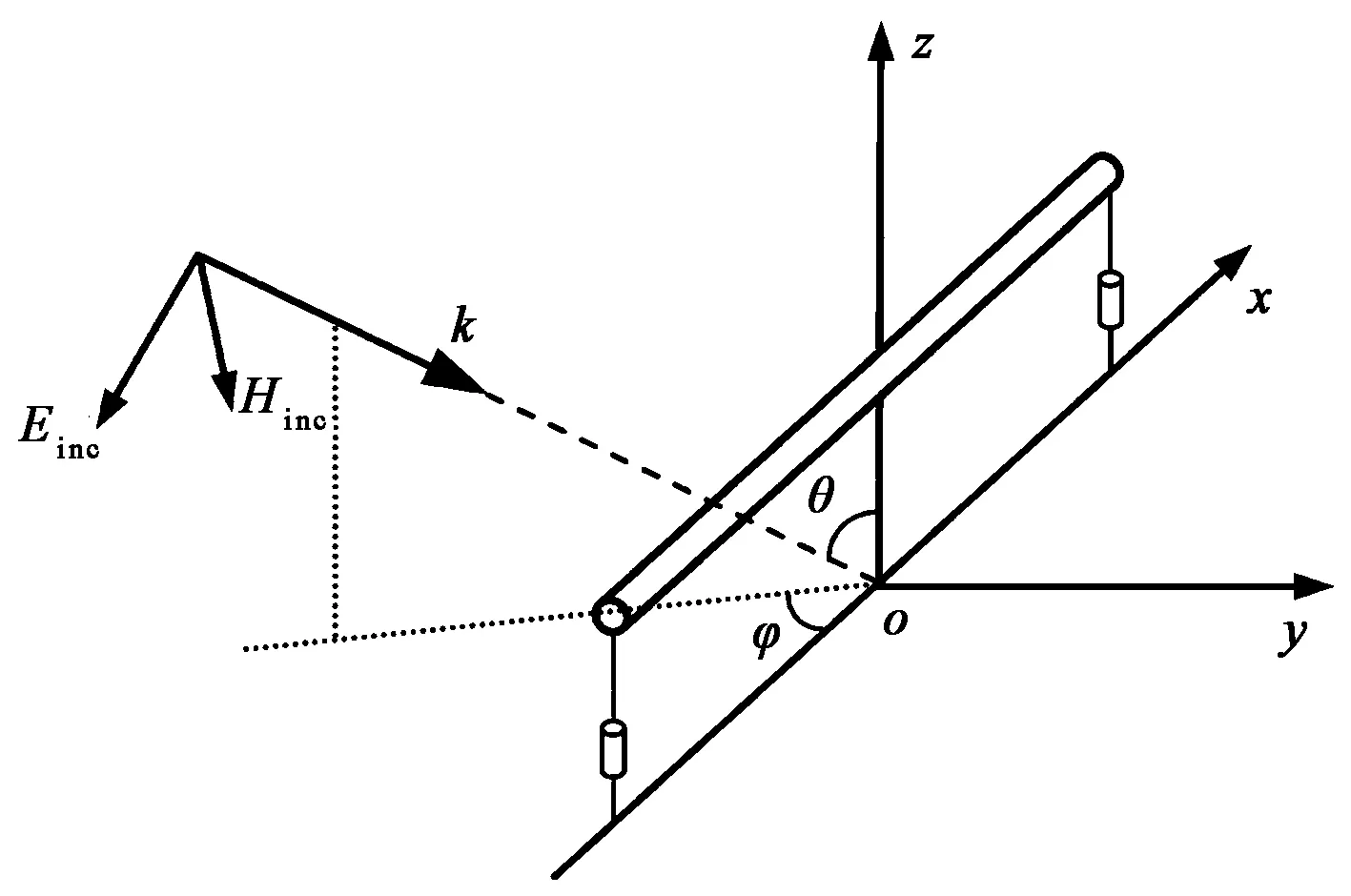
(a) 电磁脉冲激励架空线缆示意图

(b) 架空线缆模型剖面图图1 场线耦合模型

1.2 激励源

为比较不同带宽入射波条件下架空线缆的耦合效应，计算中涉及到三种高功率电磁环境：LEMP(IEC 61643-1)、HEMP(贝尔波形)和HEMP(IEC 1000-2-9)，本文中分别简称为：LEMP，HEMP1和HEMP2，其数学表达式均采用以下双指数函数表示

E(t)=kE0(e-α t-e-β t)，

(1)

式中：

LEMP：k=1.043,α=1.473×104s-1，β=2.08

×106s-1;

HEMP1:k=1.05,α=4×106s-1，β=4.76×108s-1；

HEMP2：k=1.3，α=4×107s-1，β=6×108s-1.

基于傅里叶变换，双指数函数的频域解析式为

(2)

其能量的频谱累积解析式为

(3)

式中w0为总能量.

依据式(3)，以上三种双指数型脉冲的特征参数列于表1，表中：tr为上升时间；thw为半峰值宽度.相比较而言，LEMP的tr最长，thw最大，频带最窄；HEMP2tr最短，thw最小，频带最宽.表2给出了三种脉冲不同频段能量占总能量的百分比.其中，对LEMP而言，99.6%的能量集中在1 MHz以下，最大能量频段为104～105Hz，该频段对应波长为几千到几十千米级；对于HEMP1，98.2%的能量集中在100 MHz以下，最大能量频段为106～107Hz，对应波长为几十到几百米级；而HEMP2，99.7%的能量集中在1 GHz以下，最大能量频段为107～108Hz，对应波长为几米到几十米级.

表1 三种双指数型脉冲波形特征参数对比

表2 三种脉冲不同频段能量占总能量的百分比

入射LEMP和HEMP在地面附近视为平面波，其电场时域表达式取以上三种双指数脉冲.为了说明入射波的极化方向，在等相位面上规定一个参考矢量k×z，其中k为单位波矢量，z为z坐标单位矢量.设入射波的电场矢量与参考矢量之间的夹角为ψ，以此来表示入射波的极化方向.

1.3 计算方法

高功率电磁环境作用下架空线缆耦合属电磁散射问题，首先利用FDTD法分析图1所示模型，求出空间电磁场分布，再由安培环路定律，沿线缆外表面对磁场环路积分求得外导体电流.整个计算区域分为地上和地下两个部分，地上部分为无耗自由空间，采用PML吸收边界条件截断计算域，地下部分为有耗空间，需采用有耗介质中的PML吸收边界条件截断计算域.用FDTD法计算散射问题时通常将计算区域划分为总场区和散射场区.根据等效原理，在总场区和散射场区的连接边界上设置入射波电磁场的切向分量可保证入射波只引入总场区.对于空气-大地分层介质中的散射问题，见图2，由于受地面的影响，不能简单地将自由空间中的初始入射波加在连接边界上.应利用电磁波反射、透射原理，连接边界地上部分引入的入射波是初始入射波和地面反射波的叠加；地下部分则为初始入射波在地下的透射波[15].

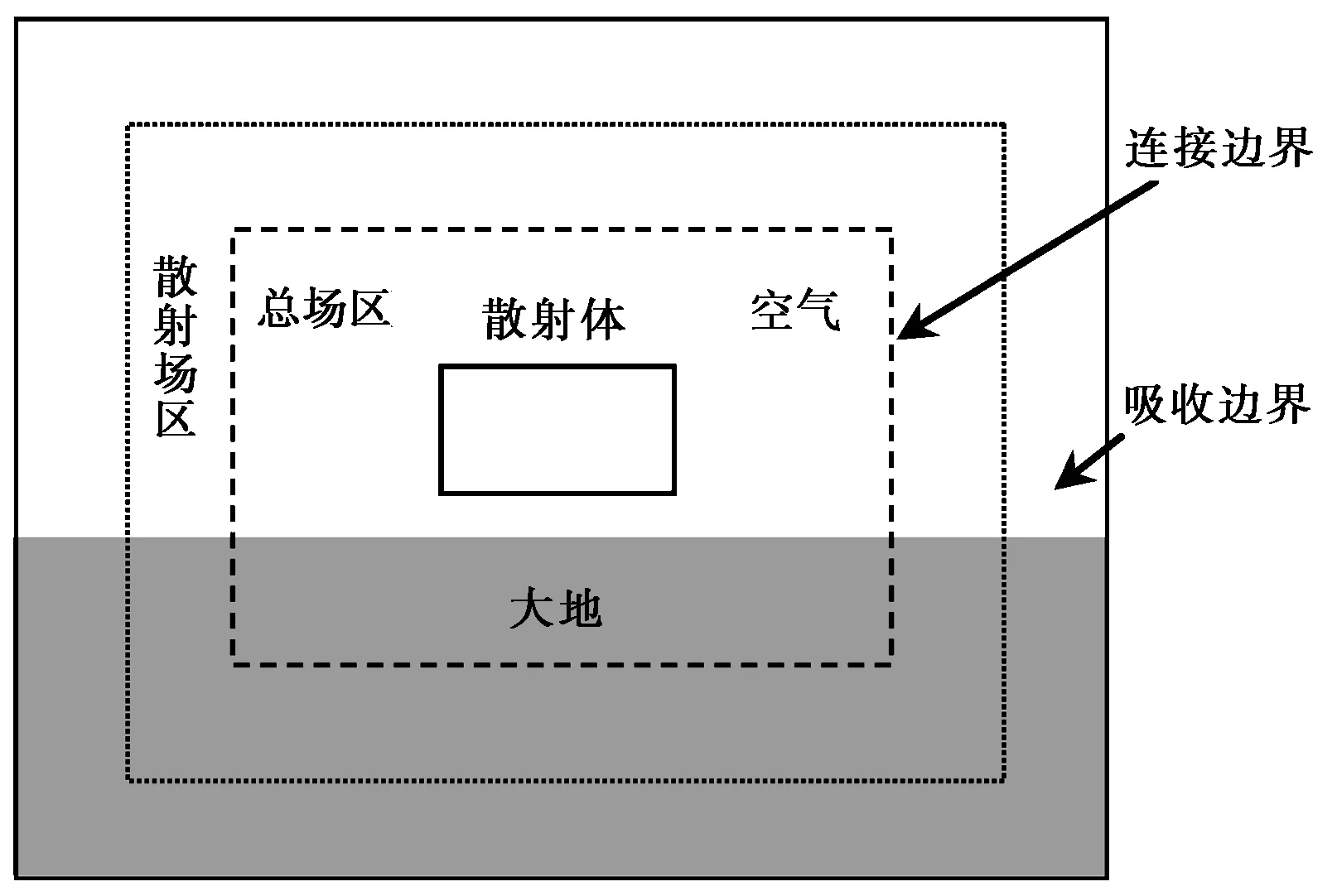
图2 空气-大地分层介质总场/散射场

2 计算结果及分析

通过计算三种电磁脉冲与架空线缆耦合的外导体感应电流和终端电压，研究不同极化方向和不同线缆长度情况下场线耦合效应的变化规律，并分析引起这些变化的原因.

2.1 不同入射波极化方向对场线耦合效应的影响

为分析不同入射波极化方向对场线耦合效应的影响，取极化角Ψ=0°、45°和90°，h=1 m，θ=30° 和φ=90°，分别计算了三种电磁脉冲入射下架空线缆中点感应电流，计算结果示于图3～5.

由图3～5可以看出，不同入射波极化方向对场线耦合效应影响较大，当Ψ=0°即入射电场方向与线缆轴向一致时，耦合效应最严重；当Ψ=90°即入射电场方向与线缆轴向垂直时，感应电流很小，耦合效应可忽略不计.

图3 不同极化方向LEMP入射下架空线中点感应电流

图4 不同极化方向HEMP1入射下架空线中点感应电流

图5 不同极化方向HEMP2入射下架空线中点感应电流

2.2 不同线缆长度对场线耦合效应的影响

取h=1 m，Ψ=0°、θ=30° 和φ=90°，分别计算了三种电磁脉冲作用下，架空线缆取不同长度时其中点感应电流和终端感应电压，计算结果如图6、7、8所示.

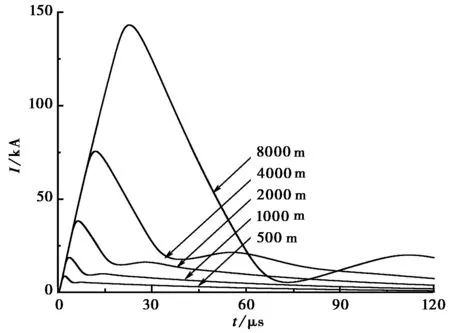
(a) 中点感应电流

(b) 终端感应电压图6 LEMP作用下不同长度架空线中点感应电流和终端感应电压

(a) 中点感应电流

(b) 终端感应电压图7 HEMP1作用下不同长度架空线中点感应电流和终端感应电压

由图6、7、8可以看出，在三种电磁脉冲作用下，随线缆长度增加，架空线缆中点感应电流和终端电压上升沿陡度不变，但峰值变大，波形变宽.当线缆长度与入射波长相比为电小尺寸时，峰值增加较快；当线缆长度增加到一定程度，即线缆长度与入射波能量最集中频段波长可相比拟时，其峰值变化趋于平稳，具体为：当频带较窄的LEMP作用时该长度为几千米以上量级，HEMP1作用时为几百米量级，频带最宽的HEMP2作用时为几十米量级.另外，在相同条件下，LEMP对线缆耦合效应最强，HEMP1次之，HEMP2最弱，这是由于对相同峰值入射波而言，LEMP总体能量与单位频段能量最大，而HEMP2总体能量与单位频段能量最小.

(a) 中点感应电流

(b) 终端感应电压图8 HEMP2作用下不同长度架空线中点感应电流和终端感应电压

3 结 论

采用并行FDTD技术，研究了在三种覆盖频段不同的高功率电磁环境作用下架空线缆的耦合效应.通过计算架空线缆的外导体感应电流和终端电压，分析了不同线缆长度、不同入射波极化方向下架空线缆耦合效应的变化规律.研究结果表明：1)入射波电场方向与线缆走向是否一致或一致的情况如何，将对耦合效应的强弱起决定性影响，当二者一致时，耦合效应最为严重；2)线缆外导体感应电流和终端电压在线缆长度增加时上升沿陡度不变，但峰值有所增加，波形变宽.当线缆长度增加到一定程度，其峰值变化趋于平稳，该长度与入射波波长有关：LEMP入射时最长，HEMP2入射时最短；3)在相同条件下，LEMP对线缆耦合效应最强，HEMP1次之，HEMP2最弱.以上结论对于带有长线缆的电子、电气系统如何根据不同高功率电磁环境的频谱特征，针对最严重的高功率电磁环境，采取相应的防护措施，具有重要指导意义.

[1] International Electrotechnical Commission. IEC 61000-2-13 Electromagnetic Compatibility(EMC)-Part 2-13 Environment-high-power Electromagnetic(HPEM) Environments-Radiated and Conducted[S/OL]. 1st ed. (2005-03-09)[2012-09-20]. http://www.iec.ch/emc/basic_emc/basic_emc_environment.htm

[2] KODALI V P. Engineering Electromagnetic Compatibility: Principles, Measurements, Technologies, and Computer Models[M]. New York: Wiley Publishing, 1996.

[3] 周璧华, 陈 彬, 石立华. 电磁脉冲及其工程防护[M]. 北京: 国防工业出版社, 2003.

[4] PAUL C R. Introduction to Electromagnetic Compatibility[M]. New Jersey: John Wiley & Sons, 2006.

[5] VANCE E E. Coupling to Shielded Cables[M]. New York: John Wiley&Sons Press, 1978.

[6] TESCHE F M, LANOZ M V, KARLSSON T. EMC analysis methods and computational models[M]. New York: John Wiley & Sons Press, 1999.

[7] BEILFUSS J, BELL A, GRAY B, ETC. Multiconductor cable response dependency on propagation modes[C]// IEEE International Symposium on EMC, 1988: 2-4.

[8] GREETSAI V N. Response of long lines to nuclear high-altitude electromagnetic pulse[J]. IEEE Trans on EMC, 1998, 40(3): 348-354.

[9] TESCHE F M. Comparison of the transmission line and scattering models for computing the NEMP response of overhead cables[J]. IEEE Trans on EMC, 1992, 34(2): 93-99.

[10] POKHAREL R K, ISHII M, BABA Y. Numerical electromagnetic analysis of lightning-induced voltage over ground of finite conductivity[J]. IEEE Trans EMC, 2003, 45(1): 651-656.

[11] 陈 彬, 王廷永, 高 成, 等. 电磁脉冲作用下近地电缆外皮感应电流的全波分析[J]. 微波学报, 2000, 16(5): 549-593.

CHEN B, WANG T Y, GAO C, et al. Full-wave analysis of the EMP induced current in cables near the ground[J]. Journal of Microwaves, 2000, 16(5): 549-553. (in Chinese)

[12] TAFLOVE A. Computational Electrodynamics: the Finite-difference Time-domain Method[M]. Boston: Artech House, 1995.

[13] 余文华, 苏 涛, MITTRA R, 等. 并行时域有限差分[M]. 北京: 中国传媒大学出版社, 2005.

[14] WANG H L, XUE Z H, YANG S M, et al. Near field scattering analysis with parallel FDTD algorithm[C]//IEEE International Symposium on Microwave, Antenna, Propagation, and EMC Technologies for Wireless Communication Proceedings. August 8-12, 2005: 796-799.

[15] YI Y, CHEN B, FANG D G. A new 2-D FDTD method applied to scattering by infinite objects with oblique incidence[J]. IEEE Trans Electromagn Compat, 2005, 47(4): 756-762.