波纹管内层流脉动传热和阻力特性的数值研究

喻九阳，聂思皓 ，郑小涛 ，林 纬,2

(1.武汉工程大学机电工程学院，湖北 武汉 430074； 2.武汉理工大学机电工程学院，湖北 武汉 430070)

0 引 言

波纹管是一种大小圆弧相切、内外波形如波纹状的薄壁管子，可通过液压成型、机械胀型、滚压成型等方法进行加工得到.作为一种高效强化换热管，国内外的研究人员对波纹管的传热和流动特性进行了各种研究[1-2].总体上讲，所有研究成果均表明波纹管具有显著的强化传热效果.

脉动流是指流量及相关参数按照某种规律(如正弦)周期变化的流体.通常认为，流体的脉动能改变边界层的厚度、抑制污垢的形成，从而降低热阻，达到强化传热的目的.但是目前的研究成果对脉动流对传热的影响没有取得一致的结论.Mackley M R等[3]认为脉动流能强化传热，而Himadri Chattopadhyay、Valueva E P等[4-5]认为脉动流传热对应的边界条件和脉动流流动参数决定了脉动流是否能强化传热.

关于波纹管和脉动流同时使用能否实现复合强化传热方面的研究还很少[6-7]，基于此，本文利用Fluent软件数值模拟了恒壁温条件下波纹管管内层流脉动的传热和阻力特性，探讨实现复合强化传热的可能性.

1 模型及边界条件

1.1 模型的简化假设

(1)流体不可压缩.

(2)忽略重力影响.

(3)流体物性保持不变.

(4)壁面速度无滑移.

(5)忽略纵向速度、温度和压力等的变化.

管内流动与换热为轴对称分布，为简化问题只取管子轴线上半部分为研究对象，因此问题被简化为二维常物性、非稳态、轴对称传热与流动问题.

1.2 几何模型

波纹管的结构示意图如图1所示(单位：mm).波纹管总长L=1 820 mm，大圆弧半径R1=12 mm，基管直径D=19 mm，波距a=18 mm，小圆弧半径R2根据几何参数R1、D和a确定.波纹管共有92个波节，为消除进出口段的影响，在管的前后各增加了一长度为70 mm的直管段.

1.3 网格与边界条件

利用Gambit软件采用结构化四边形网格对几何模型进行网格划分，考虑到边界对传热和流动的影响，对壁面附近的网格进行加密.

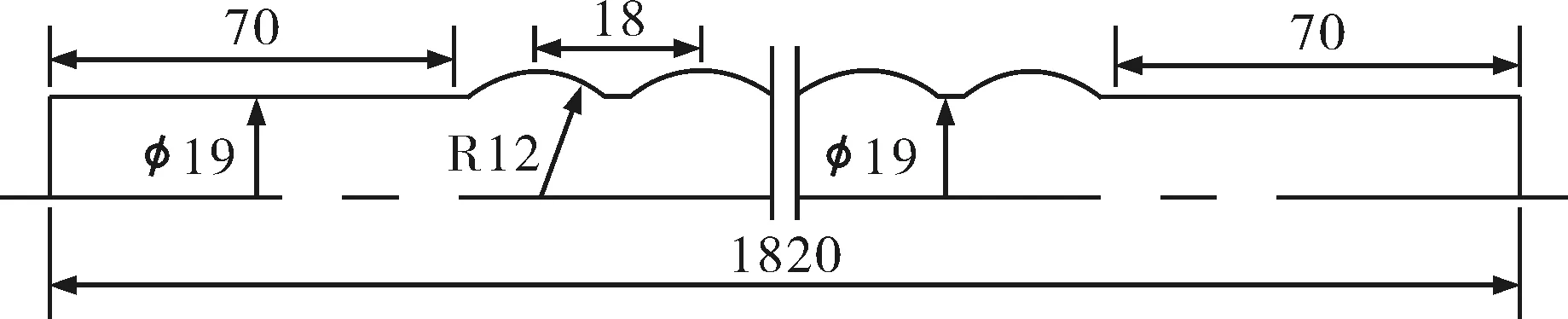
图1 波纹管结构示意图Fig.1 Schematic of corrugated tube

管内工作介质为水，入口温度为333 K.水在333 K时各物性参数如表1所示.

管入口流速由用户自定义程序UDF输入，其表达式为

vi=vs[1+Asin(2πft)]

(1)

表1 水在333 K时的物性参数Table 1 Parameters of water when temperature is 333 K

其中，vi为入口流体的瞬时速度，vs为稳态速度，计算时取0.02 m/s；A为脉动流的无量纲振幅，分别取0.2、0.4、0.6、0.8、1；f为脉动流的频率，分别取2 Hz、4 Hz、5 Hz、8 Hz、10 Hz.

壁面边界条件为恒壁温，壁面温度tw=293 K.出口设定为压力出口，压力为0.

2 数值结果分析

2.1 参数定义

平均对流换热系数为

(2)

式(2)中，qm为管内流体的质量流量，kg/s；cp为流体的比热容，kJ/(kg·K)；ΔT为流体进出口的温差，K；A为换热面积，m2；Δtm为流体与壁面的对数平均温差.

沿程阻力损失为

(3)

式(3)中：Δpf为管进出口的压强降，Pa；ρ为水的密度，kg/m3.

为分析流体脉动相比稳态时的换热效果，定义传热强化系数为

(4)

式(4)中，αp为有脉动条件下周期平均对流换热系数，W/(m2·K)；αs为稳态条件下的平均对流换热系数，W/(m2·K).

为分析流体脉动相比稳态时的沿程阻力情况，定义沿程阻力增强系数[8]为

(5)

式(5)中，hfp为有脉动条件下管沿程阻力损失的周期平均值，J/kg；hfs为稳态条件下管沿程阻力损失，J/kg；Δpfp为有脉动条件下管进出口压强降的周期平均值，Pa；Δpfs为稳态条件下管进出口的压强降，Pa.

为评价管内脉动对传热和流动的综合效应，定义效应评价准则数[9]为

(6)

当E>0时，表明强化换热的效果比沿程阻力损失的增大更显著.

2.2 脉动流对波纹管传热性能的影响

在不同无因次振幅A条件下，传热强化系数E(α)与脉动频率f之间的关系如图2所示.在A=0.2、0.4、0.6、0.8时，E(α)随着f的增大先增大后减小然后再增大；当A=1时 随着f的增大一直增大.当A<0.8时，在各频率条件下传热总是被弱化；当A=0.8时，在f<3 Hz的条件下传热被弱化，在f≥3 Hz条件下传热被强化；当A=1时，在各频率条件下传热均被强化.A=1且f=10 Hz条件下强化传热效果最好，相比稳态流传热被强化约5.9%.

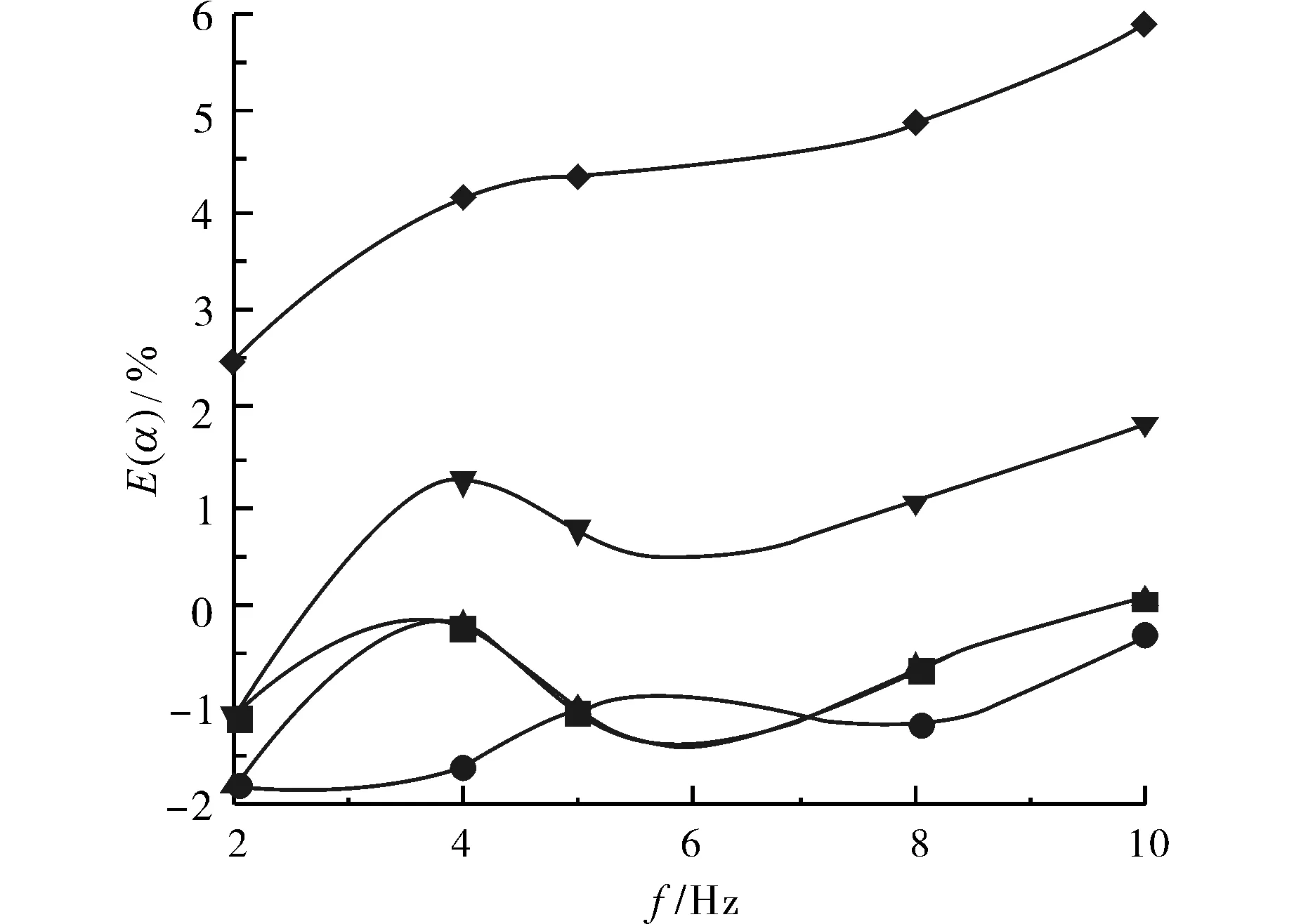
图2 不同振幅下E(α)与f的关系Fig.2 The relationship between E(α) and f when A changes 注：

2.3 脉动流对波纹管阻力特性的影响

在不同无因次振幅A条件下，沿程阻力增强系数E(λ)与脉动频率f之间的关系如图3所示.在A一定的条件下，E(λ)随着f的增大而减小；在f一定的条件下，E(λ)随着A的增大而增大.A越大、f越小则E(λ)越大，在A=1且f=2 Hz条件下，沿程阻力损失相比稳态流增大了约13.2%.这说明脉动流会使波纹管的沿程阻力增大，强化传热是以增大沿程阻力为代价的.

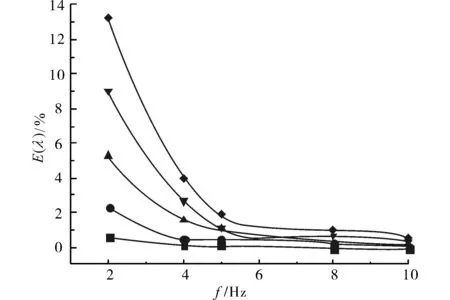
图3 不同振幅下E(λ)与f的关系Fig.3 The relationship between E(λ) and f when A changes 注：

2.4 脉动流对传热和阻力综合效应的评价

在不同无因次振幅A条件下，效应评价准则数E与f的关系如图4所示.

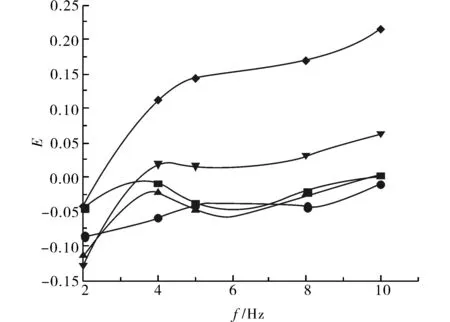
图4 不同振幅下E与f的关系Fig.4 The relationship between E and f when A changes 注：

从图4中可以看出，当A≥0.8时，而且在f≥4 Hz的条件下，E>0，在其它条件下E均小于零.这表明，尽管脉动流在强化传热的同时不可避免的带来了沿程阻力的增加，但是在此条件下强化传热的效果较沿程阻力的增加更加显著，波纹管与脉动流一起使用能起到复合强化传热的效果.

3 波纹管内脉动流强化传热原因的分析

稳态条件下波纹管第78个波节处的速度矢量图如图5所示(单位：m/s).稳态时，流体在波峰附近形成逆时针方向的漩涡，但此区域流体的速度比主流区的速度低得多，接近于0，使得此区域变成不参与热量或质量交换的传热或传质的死区，导致边界层厚度增加，总传热系数降低[10].

图5 稳态条件下的速度矢量图Fig.5 Diagrams of velocity vectors of steady flow

脉动频率f=10 Hz、无量纲振幅A=1条件下第78个波节处在一个脉动周期内不同时刻时的速度矢量图如图6(a)～(e)所示.在前半个周期内，流体均向前流动；在半周期附近时，漩涡从波峰附近形成并向主流区移动，随后又向波峰处移动，直至最后消失.漩涡在移动的过程中加剧了热量从主流体向波峰附近低温流体的移动，使得传热性能得到一定的改善.同时，由于漩涡的不断形成和消失，导致管道的沿程阻力系数随之增大.

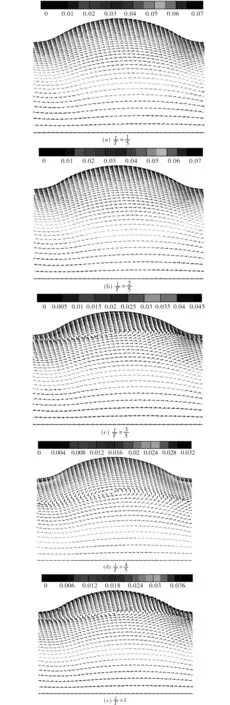
图6 脉动条件下的速度矢量图Fig.6 Diagrams of velocity vectors of pulsatiuy flow

4 结 语

利用数值计算，研究了管内层流脉动条件下波纹管的传热和阻力特性，得到如下结论：

a.在本文条件下，管内脉动流既能强化波纹管的传热也能弱化传热；相比稳态流条件，传热最大被强化约5.9%.

b.脉动流会增大波纹管的沿程阻力；传热的强化是以增大沿程阻力为代价的.

c.综合考虑脉动流对传热和沿程阻力的影响，在A≥0.8且f≥4 Hz条件下管内脉动与波纹管能起到复合强化传热效果.

d.脉动流条件下波节附近漩涡周期性的产生和消失是传热被强化和沿程阻力增加的主要原因.

致谢

本文的研究工作得到了国家自然科学基金项目(No.50976080)——《列管式换热器流体诱导振动强化传热机理研究》的资助.

参考文献：

[1] 肖金花, 钱才富, 王凤林,等. 波纹管对高黏度介质的强化传热研究[J]. 北京化工大学学报：自然科学版,2007,34(1):53-57.

[2] 俞接成, 杜晓萌. 波纹管层流传热与流动的三维数值模拟[J]. 北京石油化工学院学报,2011,19(4):11-16.

[3] Mackley M R, Stonestreet P. Heat transfer and ass-ociated energy dissipation for oscillatory flow in baff-led tubes [J]. Chemical Engineering Science,1995,50(14):2211-2224.

[4] Chattopadhyay H, Durst F, Ray S. Analysis of heat transfer in simultaneously developing pulsating laminar flow in a pipe with constant wall temperature[J]. International Communications in Heat and Mass Transfer,2006(33):475-481.

[5] Valueva E P. Hydrodynamics and heat transfer in pulsating turbulent flow of gas in a heated pipe[J]. High Temperature,2006(44):120-128.

[6] 汪威, 喻九阳, 杨侠,等. 波节管脉冲流强化对流换热数值分析[J]. 武汉工程大学学报,2010,32(3):89-91.

[7] 林纬, 喻九阳, 吴艳阳,等. 横纹管脉冲流流动与换热数值分析[J]. 武汉工程大学学报,2011,33(5):89-93.

[8] 胡玉生, 曾丹苓, 李友荣,等. 恒壁温下管内流体脉动流动对流换热的数值模拟[J]. 工业加热,2006,35(1):3-6.

[9] 林宗虎, 汪君, 李瑞阳,等. 强化传热技术[M].北京：化学工业出版社,2007.

[10] 肖金花, 钱才富, 黄志新,等. 波纹管传热强化效果与机理研究[J]. 化学工程,2007,35(1):12-15.