基于粗糙集的社区卫生服务满意度评价

李丽清，许跃峰，周小军，李钟捷

社区卫生服务是立足于社区，为社区居民提供优质卫生服务的第一层面接触。就诊居民对社区卫生服务的满意程度直接影响到社区卫生服务的生存环境[1]。本研究采用分层抽样与拦截式现场调查相结合的方法，对南昌市东湖区、青山湖区、西湖区、湾里区、青云谱区五个行政区的社区卫生服务机构就诊居民进行满意度调查，以期为南昌市社区卫生服务机构均衡、有序发展提供决策依据。

1 满意度的内涵

查阅文献发现，满意度的定义到目前还没有一个统一的体系。《质量管理体系基础和术语》(GB/T9000-2000idt ISO2000)中“顾客满意”的定义为顾客对其要求已被满足的程度和感受。从服务业的角度来看，顾客满意度是用消费者的消费经验来衡量产品和服务质量的一种指标，体现了企业所服务的市场(顾客)购买与消费情况的总体评价，包括产品的实际使用情况和对产品的期望。

医疗行业是特殊的服务业，患者是医疗服务的利用者，即消费者；医生是医疗服务的提供者，即生产者。患者满意度的定义有如下几种说法，有的学者提出患者满意度是指人们由于健康、疾病、生命质量等诸方面的要求而对医疗、保健服务产生的某种期望，基于这种期望，对所经历的医疗保健服务情况进行的评价[2]。从这个定义可看出，患者满意度是患者感受值与期望值的比值，它是医疗保健接受者对其医疗经验包括结果、内容等各方面的反映，是同主观性感受相关联的，包含对过去接受的医疗服务的平均感受，患者由经验值形成他认为医疗服务应该达到的水平。因此，从卫生服务的角度来讲，患者满意度是指人们由于健康、疾病、生命质量等方面的要求而对医疗、保健服务产生的某种期望，并对所获得的医疗、保健服务进行比较后产生的情感状态的反应[3]。

综上所述，本研究认为患者对社区卫生服务的满意度是指就诊居民接受医疗行为后的实际感受与其在接受医疗服务之前的预期感知比较，这种接受服务后的感受与接受服务前的感知是来自患者与社区卫生服务机构两方面的多种因素的综合，其中患者自身的因素包括性别、年龄、职业、收入状况等，而来自社区卫生服务机构方面的因素包括就医环境、服务态度、尊重程度、解释交流、服务价格、隐私保护、没有过度医疗等因素。因此，患者满意度是这些因素的函数，可表示为：PS=F(f1,f2)，f1=(mi)，f2=(nj)。mi是来自医疗服务消费者自身因素的集合，在这里(i=1,2,3,4)代表就诊居民的性别、年龄、职业、收入状况等；nj是来自医疗机构因素的集合，在这里(j=1,2,3,4,5,6,7)代表就医环境、服务态度、尊重程度、解释交流、服务价格、隐私保护、没有过度医疗等因素[4]。

2 粗糙集理论

2.1 粗糙集简介[5-6]粗糙集理论是波兰科学家Z.Pawlak教授在1982年提出的一种数据推理方法。它不需提供问题所需处理的数据集合之外的任何先验信息，仅根据观测数据删除冗余信息，从数据集发现一些隐藏的模式和关系，在保留关键信息的前提下对数据进行化简并求得知识的最小表达；能识别并评估数据之间的依赖关系，分析不完整知识的程度——粗糙度、属性间的依赖性与重要性、生成分类或决策规则等。粗糙集理论是建立在分类机制的基础上的，它将分类理解成在特定空间上的等价关系，而等价关系构成了对该空间的划分。粗糙集理论的关键思想是利用已知的知识库，将不确定的或不精确的知识用已知的知识库中的知识来近似地刻画。该理论的特点：它不需要提供除问题所需处理的数据集合之外的任何先验信息，所以对问题的不确定性的描述和处理相对客观。

2.2 本研究将用到的粗糙集的几个基本概念

2.2.1 知识 知识是人工智能中一个非常重要的概念，在粗糙集理论中，知识被看做是关于论域的划分，是一种对对象进行分类的能力。用集合的概念表示：设U是非空有限论域，R是U上的二元等价关系，知识就是等价关系集R对U划分的结果，记为U/R。属于R中所有的关系对U的划分称为知识库，记为A=(U,R)。设R是U上的一个等价关系，U/R={X1,X2,…Xn}表示R产生的分类，称为关于U的一个知识。

2.2.2 不可区分关系 若P⊆W，且P≠Φ，则P中的全部等价关系的交集称为P上的不可区分关系，记为IND(P)：IND(P)={(x,y)∈U×U,∀α∈P,f(x,α)}=f(y,α)。

不可区分关系也称为等价关系。它把U划分为有限个集合，称为等价类。在每一个等价集合中，对象间是不可区分的，对于∀x∈U，它的P等价类定义为：[X]P={y∈U∣(x,y)∈IND(P)}。

IND(P)的所有等价类族U/IND(P)定义为等价关系P的族相关的知识，称为P基本知识或基本集合，记为U/P。因此可以看出，U/P实际上是由论域中相互不可区分的对象组成的集合，是组成知识的颗粒。

2.2.3 属性的约简 属性约简是粗糙集理论的核心内容之一，在粗糙集的信息系统中，并不是所有的属性都是同等重要的，有些属性甚至是冗余的。所谓知识约简就是在保证信息系统分类能力不变的条件下，删除其中冗余的或者是不重要的属性。

令R为一族等价关系，p∈R，如果ind(R)=ind(R-{p})，则称p为R中不必要的，反之则称p为R中必不可少的。如果每个p∈R都是R中必不可少的，则称P是独立的，否则称R为依赖的。设P⊆R，如果P是独立的，且ind(P)=ind(R)，则称P为R的一个约简。

2.2.4 基于知识信息量的属性重要度的计算 使用信息量来描述论域中的数据集合。信息表的行代表对象，列代表属性。一个属性对应一个等价关系。

设A=(U,R)为一信息系统，对于等价关系P⊆R，有分类U/Ind(P)={X1,X2,…,Xn}，则P的信息量记为：

在这里，|*|表示集合的基数，即集合中所含元素的个数。属性attr在属性集P中的重要度定义为：

sigp- |attr|(attr)=I(P)-I(P-{attr})……(2)。

其中，attr为某个属性；P⊆R为等价集R中的一个等价子集。将属性集中的每个属性重要度归一化，即得到各个属性的权重。

3 社区卫生服务满意度实证评价

3.1 确定评价对象集及指标集 本研究在对南昌市社区卫生服务机构系统调研的基础上，自行设计问卷，其内容包括就医环境、服务态度、尊重程度、解释交流、服务价格、隐私保护、没有过度医疗等方面的满意度调查。于2012年1—4月，采用分层抽样与拦截式现场调查相结合的方法，先将南昌市5个城区分层，每个城区为一层，从每个城区中抽取2个社区卫生服务中心和2个社区卫生服务站进行调查，中心与站的选择采用单纯随机抽样法[7]；社区卫生服务机构就诊居民的抽样采用在机构出口处进行拦截的调查方式开展，每个社区卫生服务中心抽样不少于30名就诊居民，每个社区卫生服务站抽样不少于20名就诊居民。通过填写调查问卷的方式进行现场调查，其目的是通过了解就诊居民在接受社区卫生服务机构提供服务时的感受及对未来的期望，以期更好地完善社区卫生服务功能，为社区居民提供更便利、有效的基层卫生服务。且问卷回收不少于500份。

本次共调查了503例社区卫生服务机构的就诊居民，其中男209例(41.6%)，女294例(占58.4%)；年龄15～90岁，平均年龄(50±17)岁(成年人由本人填写，未成年人由其监护人代填)；文化程度：不识字/识字很少者64例(12.7%)，小学70例(13.9%)，初中135例(26.8%)，高中/中专/技校158例(31.4%)，专科/本科及以上者76例(15.2%)。从调研中得知，来社区卫生服务机构就诊的居民最看重的因素为：就医环境、服务态度、尊重程度、解释交流、服务价格、隐私保护、没有过度医疗。将有效的503份问卷进行满意度分析，就诊居民对各因素的满意度情况见表1。

表1 社区居民对社区卫生服务的满意度情况〔n(%)〕

3.2 信息表的离散化 表1中的数据类型均为定距型数据，而Pawlak提出的以不可分辨关系为核心的粗糙集方法处理的是离散属性值，本研究采用组距分组的方法将表进行离散化处理。在实际分组中，可以按照Sturges提出的经验公式来确定组数K：K=1+lgn/lg2，其中n为数据个数，对结果四舍五入取整后为理论分组数目，组距可由公式：组距=(最大值-最小值)/组数来确定[8]。本研究中考虑到实际问题研究的需要，将组数K定义为3，其离散化信息表见表2。表中的辖区用Si(i=1,2,3,4,5)表示，其中S1代表东湖区，S2代表青山湖区，S3代表西湖区，S4代表湾里区，S5代表青云谱区；表中的指标用xj(j=1,2,3,4,5,6,7)表示，其中x1代表就医环境，x2代表服务态度，x3代表尊重程度，x4代表解释交流，x5代表服务价格，x6代表隐私保护，x7代表没有过度医疗。

表2 离散化的信息表

3.3 指标集约简 约简通常有两种方法：一种基于不可分辨关系的代数方法，即根据约简和核的定义运算；另一种是基于粗糙集逻辑运算的方法，即根据分辨矩阵和分辨函数进行逻辑运算[9]。按照以上约简方法，可以得到本例中的约简集：{x6,x7}；{x2,x7}；{x3,x7}；{x4,x5,x7}；{x5,x6}。根据问题的研究需要，本研究选择其中的一个约简为{x4,x5,x7}。因此，消除冗余后且不改变原有分辨能力的信息表见表3。

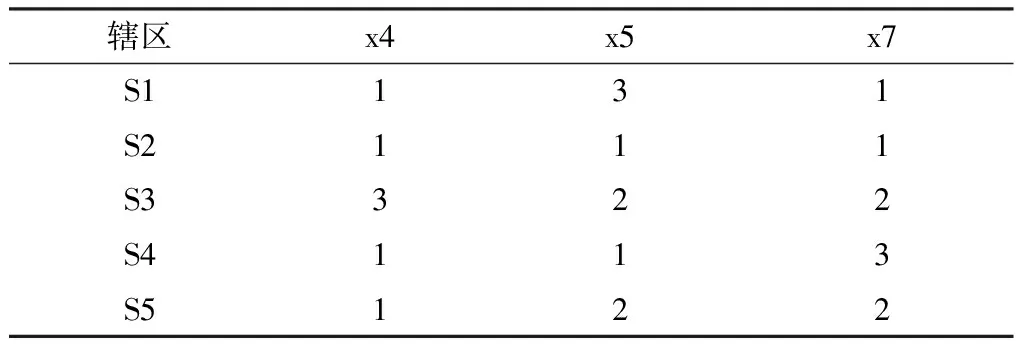
表3 消除冗余后的信息表

3.5 综合评价值计算 根据约简指标权重可以计算出南昌市五个行政区社区卫生服务满意度各指标的得分，其计算过程为将评价出来的约简指标权重乘以这三个约简指标组成的3行5列归一化矩阵，即可得出评价值Ai(i=1,2,…,5)。

Ai=(0.33，0.33，0.33)*

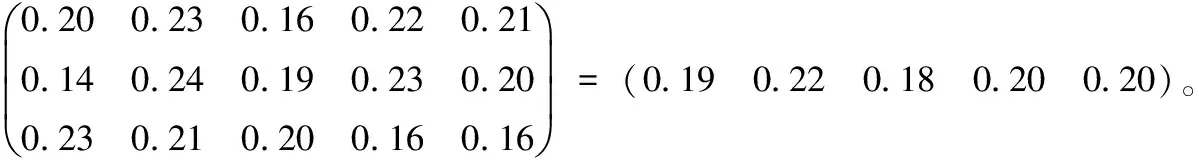
表4 约简指标集的重要度及权重系数

表5 南昌市社区卫生服务满意度的评价结果

从以上结果得出南昌市社区卫生服务满意度评价的得分，其排名顺序为：第一名：青山湖区；第二名(并列)：湾里区，青云谱区；第三名：东湖区；第四名：西湖区。

4 讨论

粗糙集最大的优势就是不需要其他的先验知识，直接从信息表中挖掘出潜在的信息，相比其他方法，所得到的数据真实客观。本研究借助粗糙集理论中的约简思想，提取关键指标并利用重要度的计算确定指标权重，克服了传统权重确定方法的主观性，结合线性加权法进行评价，使得评价结果更具客观性和准确性。

本研究以来自南昌市五个行政区503名就诊居民的现场调查数据为资料，对南昌市五个行政区社区卫生服务满意度进行实证分析，并得出排名顺序，对促进南昌市城市社区卫生服务的和谐发展具有一定的现实意义。评价结果充分说明了南昌市五个行政区的社区卫生服务发展状况不平衡，其中主要原因是服务区域的地理环境不同而导致的，不同的地理环境必然会导致不同的经济水平和管理水平。为了更好地为南昌市市民提供便利、持续、健康的社区卫生服务，社区卫生服务管理者应重视各区的均衡发展，采取相应的措施提高社区居民对社区卫生服务的满意度水平。

1 邵爽，王嵬，路孝琴，等.北京市某区外来人口社区卫生服务利用情况和满意度调查[J].中国全科医学，2012,15(1)：199.

2 Pascore GC.Patient satisfaction in primary health care[J].Evaluation and Program Planning,1993，6(3-4):185-210.

3 Judith AH,MiehaeI CD.Meta analysis of satisfaetion with medical care:Description of research domain and analysis of overall satisfaetion levels[J].Soc Sci Med,1988,27(6):637-644.

4 李丽清，刘卫东.基于粗糙集的患者满意度评价模型研究[J].数学的认识与实践，2009，39(7)：25-30.

5 Z.Pawlak.Rough sets——Theoretical aspects of reasoning about data[M].Dordrecht：Kluwer Academic Publishers,1991.

6 刘清.Rough集及Rough推理[M].北京：科学出版社，2001.

7 李钟捷.南昌市社区卫生服务现状及综合评价研究[D].南昌：南昌大学，2012.

8 薛薇.基于SPSS的数据分析[M].北京：中国人民大学出版社，2006.

9 胡寿松，何亚群.粗糙集决策理论与应用[M].北京：北京航空航天大学出版社，2006.