三维全空间等熵Euler方程的松弛近似

胡丽平，王红利

(1.河南农业大学信息与管理科学学院，河南郑州450002;2.华北水利学院数学与信息科学学院，河南郑州450011)

本文研究下列尺度化的可压的等熵的Euler方程松弛极限问题:

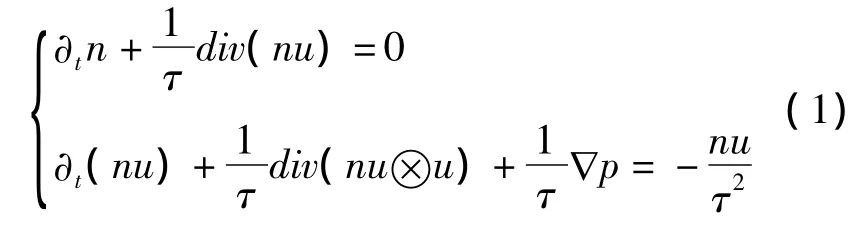
式中:n和u分别表示流体的质量密度和速度，它们都是三维空间变量x∈R3和时间变量t＞0的函数.

对动力方程运用Maxwell迭代

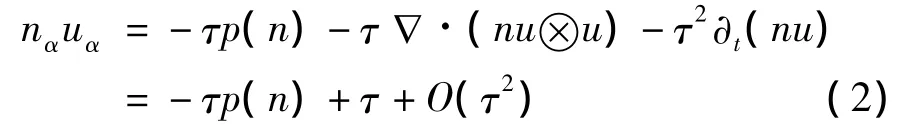
将截断nu=-τp(n)代入质量方程(1)，得到多孔介质方程:

式中:p(n)=αnγ是从(0，∞)到(0，∞)上的严格递增且光滑的压力密度函数，其中，α＞0是一个正常数，γ＞1是绝热指数.

关于不同模型的松弛极限问题有了很多研究，如EuLer-Poisson方程组［1～3］，EuLer-Maxwell方程组［4，5］.Coulombel和 Goudon在［6］中构造系统(1)在γ=1的一致光滑解并证明了相应的松弛时间极限问题.Xu在［7］中运用Littlewood-Paley分解研究了模型(1)的强松弛极限.本研究则通过改变能量方法严格证明了好的初始条件下模型(1)光滑解到多孔介质方程解的收敛性，并给出收敛率.

1 准备工作

假设n是方程(3)具有初值n(0，x)的光滑解，为(1)的解(nτ，uτ)构造具有初值

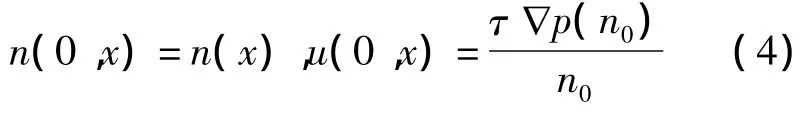
的一个形式近似解

接下来，用能量方法证明在(nτ，uτ)存在的有限时间区间内能表示为

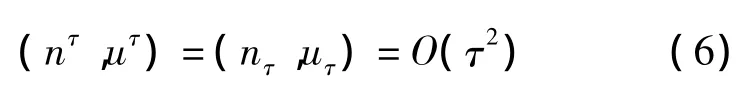
进一步，结论表明，如果方程(3)存在整体光滑解，并且n有一个正的下界，那么对任意的T＞0，存在τ0＞0，当 τ＜τ0时，使得 EuLer方程组在［0，T］存在唯一的光滑解.

将(1)写成对称的双曲系统，为此，引入焓h=h(n)＞0满足

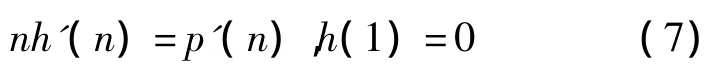
因为p(n)是严格单调的光滑函数，h(n)也是严格单调的光滑函数，从而h(n)存在反函数n=n(h).令g(h)=p'(n(h))，于是，系统(1)等价于

或者

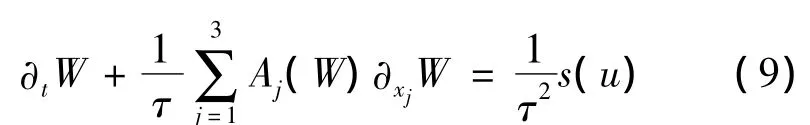
式中:W=(h，u)T，AJ(W)=(ujI4+A(h)-10Cj)，s(u)=(0，u)T，

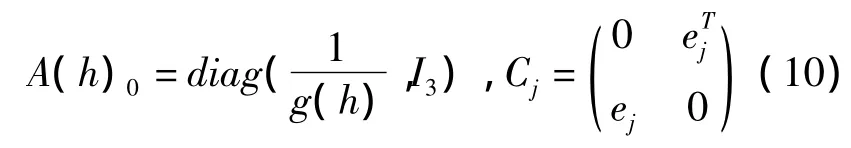
设n是多孔介质方程(3)的解，由Maxwell迭代，得

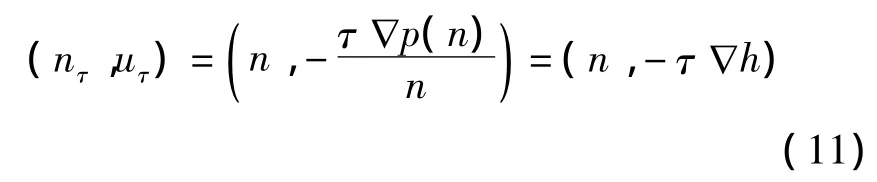
定义

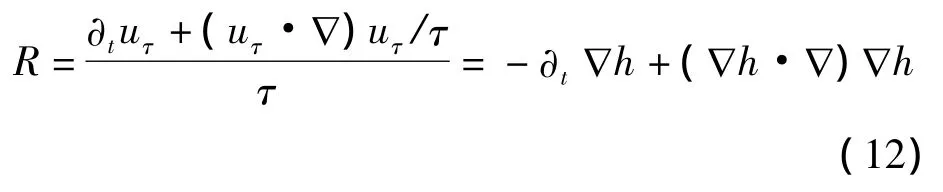
关于(nτ，uτ)，有以下存在性和正则性结果:

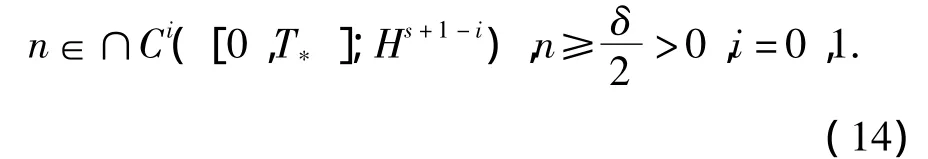
进一步

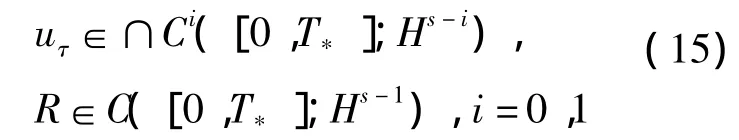
2 主要结果及证明

(h，u)(0，x)=(h(n(0，x))，- τ∇h(n(0，x)))的 Euler方程(8)或(9)有唯一的一个解(nτ，uτ)，而且存在一个不依赖τ但依赖于T*＜∞的常数M，使得

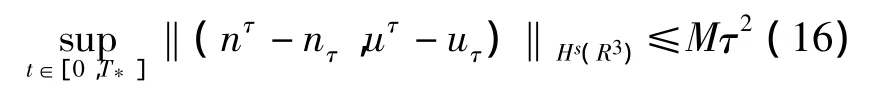
此外还有估计

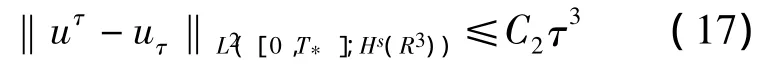
证明 记［0，Tτ］是对称的双曲系统(8)或(9)的解存在的最大区间，取 T=min{T*，Tτ}，令

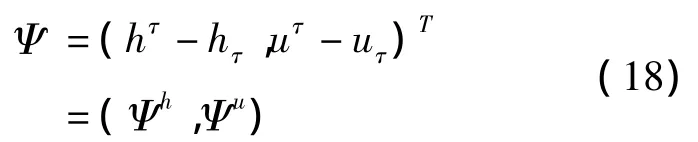
则Ψ满足

式中: Wτ=(hτ，uτ)T，Wτ=(hτ，uτ)T，S(Ψu)=(0，Ψu)T，H=(0，R)T.

易知 Ψα=Ψ，α∈N3，|α|≤s满足

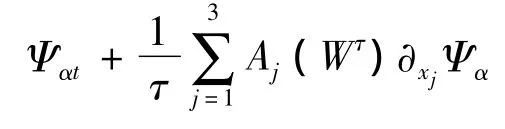
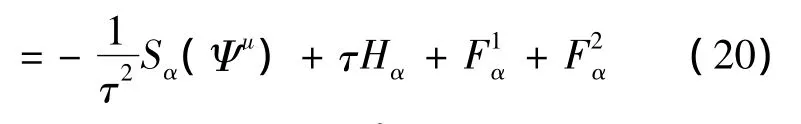
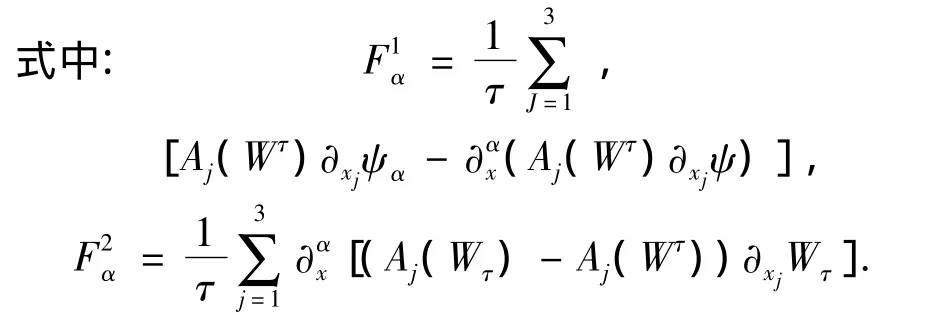
为更清楚地证明定理1，分2个引理表述:

引理2 在定理1的条件下，有

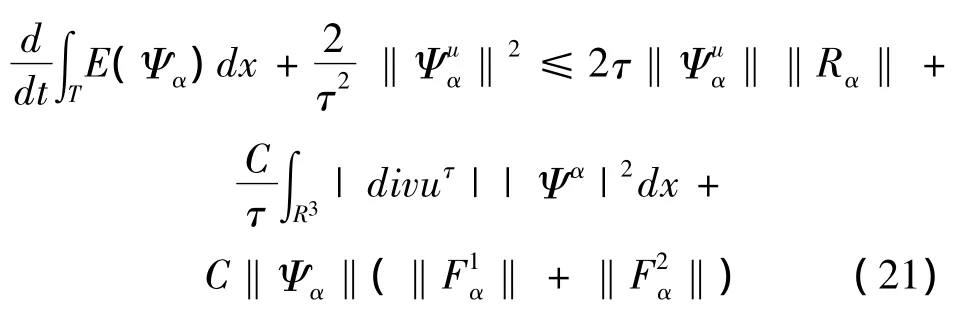
式中:E(Ψα)=

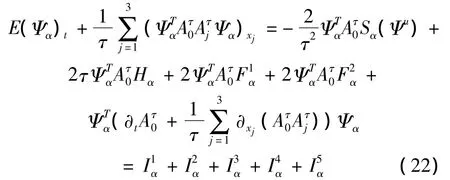
由(10)，易知

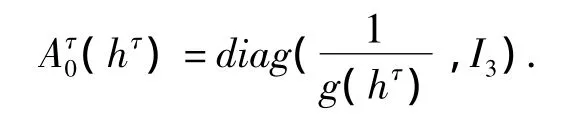
简单计算，得

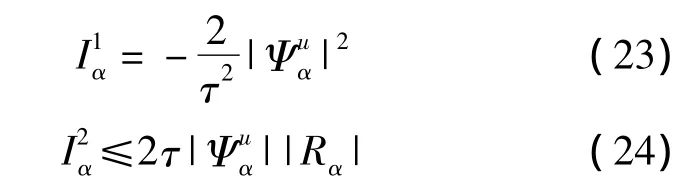
另外，因为n有正的下界，所以存在正数a，b(a＞b)使得 hτ∈［a，b］，所以

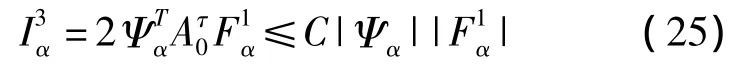
和

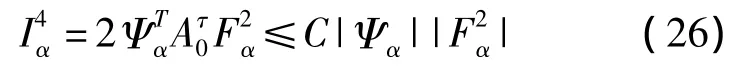
最后，有链式求导法则和(8)中关于h的方程，得

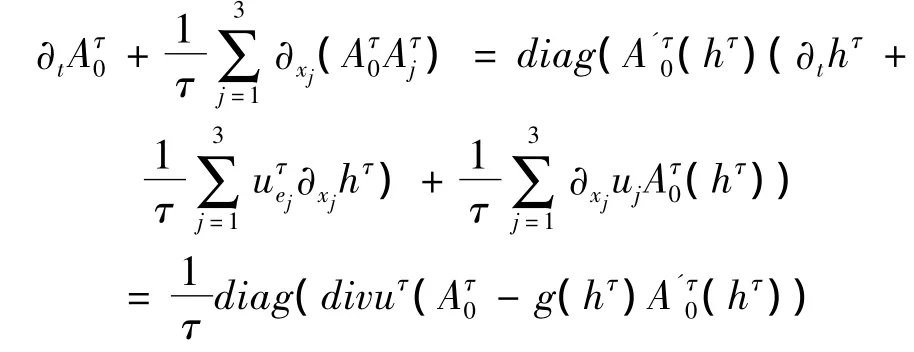
从而，有

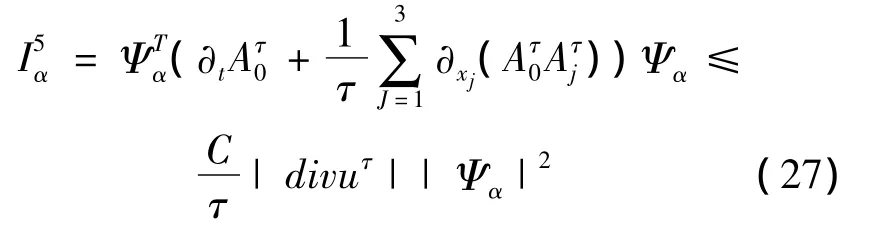
对(22)式在R3上积分即得引理2.

证明 注意到uτ=-τ∇h(nτ)，从而对s＞s0＞，s，s0∈N，由 Sobolev嵌入定理，得

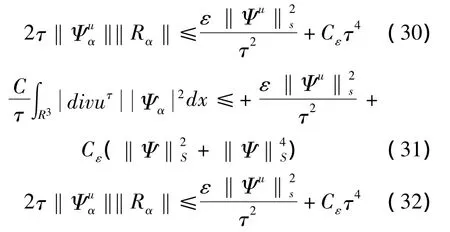
运用Cauchy不等式和Moser型微积分不等式［8，9］，有

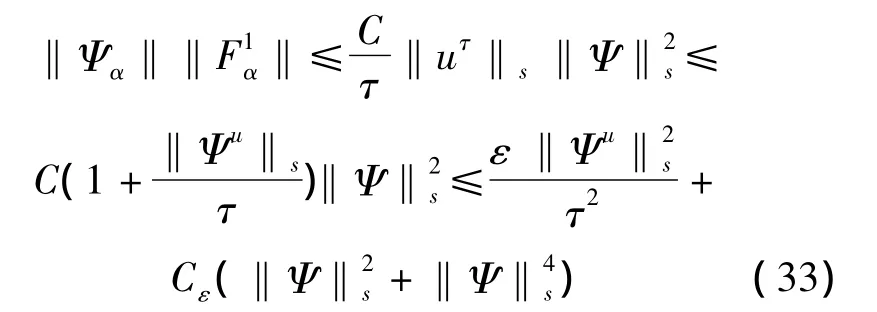
同理，有

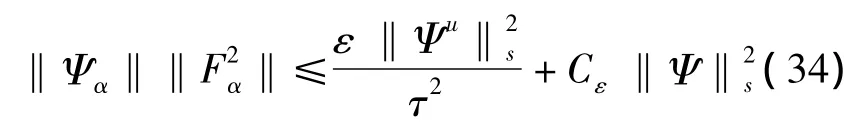
将估计(30)，(31)代入(21)，得

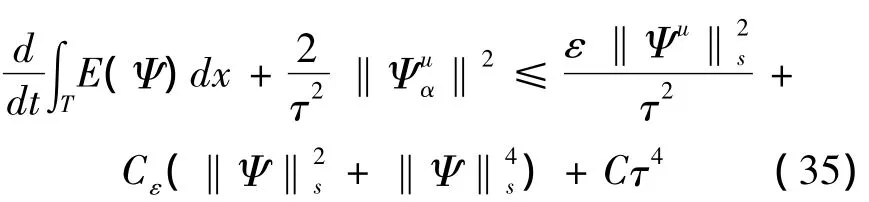
上式在(0，t)上积分并对所有|α|≤s求和，取充分小的ε，可得(28).

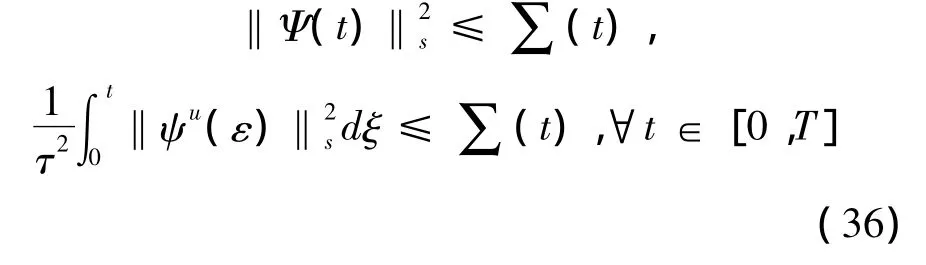
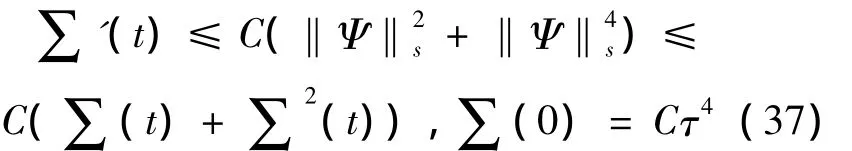
对(37)应用Gronwall不等式，得

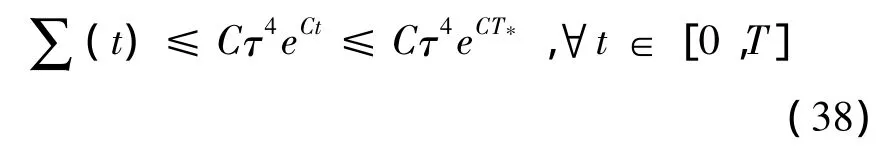
因此，由(36)，有

特别地，上式蕴含着 Ψ在时空空间 L∞(［0，Tτ］，Hs(R3)τ＞0)中一致有界，从而(nτ，uτ)也是一致有界的，通过运用标准的方法对光滑解在时间上延拓，可以得到Tτ≥T*，即T=T*，这就证明了定理1.

［1］ YONG W A.Diffusive relaxation limit of multidimensional isentropic hydrodynamic models for Semiconductors SLAM［J］.Appl Math，2004，64:737-1748.

［2］ LI Y.Realxation time limits problem for hydrodynamics models in semiconductor science［J］.Acta Mathematica Scientia，2007，27:437-448.

［3］ HSIAO L，ZHANG K The relaxation of the hydrodynamical model forvsemiconductors to the drift-diffusion equations［J］.Differential Equations，2000，165:315-354.

［4］ YANG J W，WANG S，ZHAO J.The relaxation-time limit in the compressible Euler-Maxwell equa-tions［J］.Nonlinear Anal，2011，74:7005-7011.

［5］ YANG J W，WANG S，LI Y，et al.The diffusive relaxation limit of non-isentropic Euler-Maxwell equations for plasmas［J］.Math Anal Appl，2011，380:343-353.

［6］ COULOMBEL J F，GOUDON T.The storng relaxation limit of the multidimensional isothermal Euler equations［J］.Trans Am Math Soc，2007，359:637-648.

［7］ XU J.Strong relaxation limit of multi-dimensional isentropic Euler equations［J］.Z Angew Math Phys，2010，61:389-400.

［8］ KLAINERMAN S，MAJAD A.Singular limits of quasilinear hyperbolic systems with large parameters and the incompressible limit of compressible fluids［J］.Comm Pure Appl Math，1981，34:481-524.

［9］ MAJDA A.compressible fluid flow and systems of conservation law in several space variables［M］.New York:Springer，1984.