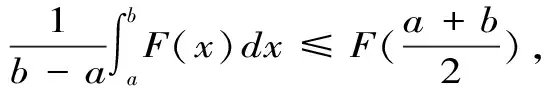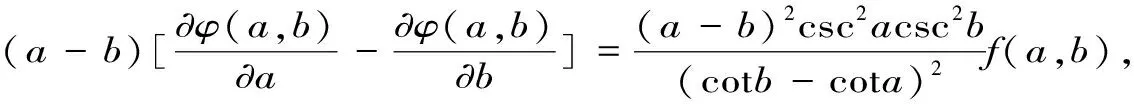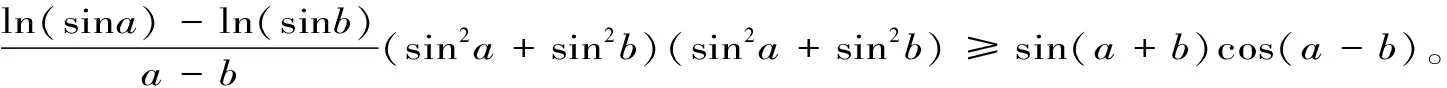两类三角平均的Schur凸性*
2013-04-13张益池
张 帆 , 张益池
(湖州职业技术学院, 浙江 湖州 313000)
1 引言
设a,b∈+,则称为两个正数a,b的算术平均,Gh.Toader和J.Sádor在文献[1]中提出了有关两个正实数a,b的三角平均:
当a≠b时,

(1)

(2)
当a=b时,Msin(a,b)=Mtan(a,b)=a。并给出不等式:Msin(a,b) 文献[2]讨论了Msin(a,b),Mtan在[0,π/2]上的Schur凸性,并加细了上述不等式,其结果是:对于a,b∈[0,π/2],a≤b,有: 本文类比文献[2],定义如下两个新的三角平均:当a≠b时, (3) (4) 当a=b时,Mcos(a,b)=Mcot(a,b)=a。 本文根据凸函数理论,证明Mcos在[0,π/2],上是Schur凸函数,Mcot(a,b)在,[0,π/2],上是Schur凹函数,并由此给出一个新的不等式链。 为证明本文的主要结果,需要如下定义和引理: 对于x=(x1,x2,…xn)∈n将x的分量递减重排后,记作x[1]≥x[2]≥…≥x[n],并用x≤y表示xi≤y1,i=1,2,…,n。 定义1[3]设x,y∈满足: 定义2[3]设Ω⊂n,φ:Ω→R。 (1)若在Ω上x≤y⟹φ(x)≤φ(y),则称φ为Ω上的增函数;若-φ是Ω上增函数,则称φ为Ω上的减函数;(2)若在Ω上xy⟹φ(x)≤φ(y),则称φ为Ω上的Schur凸函数;若-φ是Ω上Schur凸函数,则称φ为Ω上的Schur凹函数。 引理1[3]设Ω⊂n是有内点的对称凸集,φ:Ω→φ在Ω上连续,在Ω的内部Ω0可微,则φ在Ω上Schur凸(凹)的充要条件是φ在Ω上对称且对任意x∈Ω0,有: 定理1Mcos(a,b)在[0,π/2]上是Schur凸函数。 即 (5) 不妨设F(x)=sin2x,易证F(x)在[0,π/2]上为凹函数,由Hadamard不等式[5]: (6) 根据引理1可得Mcos(a,b)在[0,π/2]上是Schur凸函数。 定理2在Mcot(a,b)在[0,π/2]上是Schur凹函数。 (7) 下面证明:f(a,b)≤0 (8) 不妨设G(x)=cotx,易证G(x)在[0,π/2]上为凸函数,由Hadamard不等式[5]: 即证: 这是显然的,结论(8)式成立。 推论对于a,b∈[0,π/2],a≤b,有 参考文献: [1] Gh.Toader,J.Sádor.Inequalities for general integral means[J].Joumal of Inequalities in Pure and Applied Mathematics,2006(1):13. [2] 姜卫东.两个三角平均的schur凸性[J].高等数学研究,2008,11(2): 46-47. [3] 王伯英.控制不等式基础[M].北京:北京师范大学出版社,1990:59-61. [4] 李大矛,顾春,石焕南.Heron平均幂型推广的Schur凸性[J].数学的实践与认识,2006,36(9):387-390. [5] 匡继昌.常用不等式(第四版)[M].济南:山东科学技术出版社,2010:430.2 定义和引理
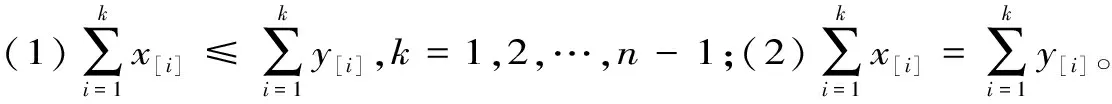

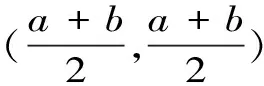
3 主要结果及其证明