对洛仑兹变换传递性的探究

李微硕

（北京理工大学 材料学院，中国 北京 102488）

时间和空间的认识需要表和尺这类在某一条件下绝对化的度量工具，因此其两者本身是客观的.但是要进行测量，仅仅依照被测物体本身是无法体现其物体的运动状态，因而需要参考系作为被测物体的一面“镜子”.在测量过程中，参考系也恰恰提供了某种特定条件的度量工具在这种环境下相对性.由于不存在绝对的时间空间，因而不同参考系下对同一事件四维坐标的表示不同但又相关，因而有了洛仑兹变换.洛伦兹变换是爱因斯坦狭义相对论的数学基础.值得研究的是，在存在三个惯性参考系下，是否可以通过已知两组惯性系间接推出第三组惯性系之间四维坐标的变换关系，即洛仑兹变换是否具有传递性.

1 建立假设模型

首先，考虑这样一种环境：在一个无限大的空间里仅存在一个质点.在这样的环境中，质点既可以说是运动的也可以说是静止的，运动是其绝对存在，然而在无限大的环境中这种运动也可以看作是相对静止.总而言之，在没有参考系的前提下其运动状态是绝对未知的.因而我们可以把参考系（通常指惯性系）理解为物质某一种运动状态函数表出的基础，对于不同参考系必然存在不同的表出，由于参考系之间有着确定的关系，因而对于同一事件在不同参考系下的表出有着一定的转换关系，即洛仑兹变换.

基于洛仑兹变换，建立如下假设模型：有S系、S′系和S″系，其各自x轴重合，y轴和z轴分别平行，已知S′系相对S系和S′系相对于S″分别沿x轴正向速度为u.

2 用矩阵形式探究其传递性

虽然在后续的资料查阅中了解到洛仑兹变换的一般矩阵表达形式[1]如下：

但由于仅讨论惯性系仅在x方向上有相对运动，故将时空坐标转换按照预先设定写成：

其中 X=[v1，v2，v3，t]T，X′=[v1′，v2′，v3′，t′]T，且有以 u 为参数的矩阵：

易证明A(u)A(-u)=I，则两者互为逆矩阵，符合相对性原理.

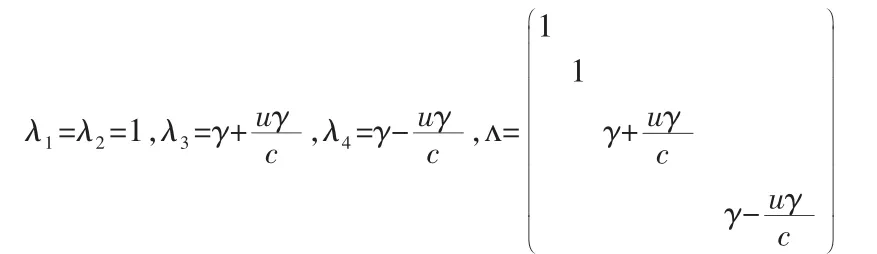
对于之前的假设模型易得到：X′=A(u)X， X″=A(u)X′，因而有 X′=A(u)A(u)X，说明当有 P-1A(u)P=ʌ(u)，由 A(u)n=PʌnP-1可进行 n 次交换.

由此表明,从矩阵变换的角度洛仑兹变换具有传递性.

然而，在此也不难发现A(2u)与A(u)A(u)不相等，由于矩阵A仅有一个可变参数u，可以推出S′系对S系相对速度实际不为2u，因此需要通过相对论速度的角度进行探究.

3 从相对论速度角度讨论其传递性

通过S系到S′系和S′系到S′系的洛仑兹转换来推导S系到S′系的洛仑兹变换：

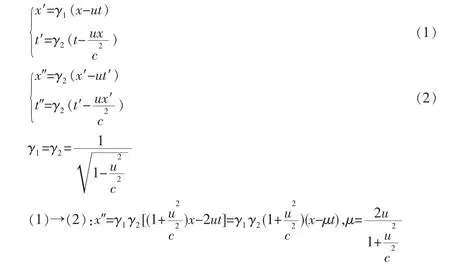
另外可知：

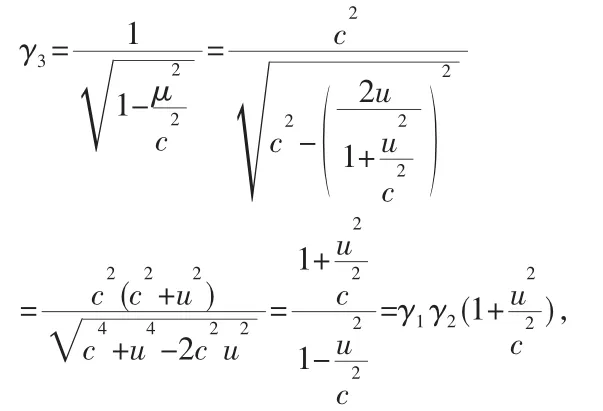
由此推出关于S系到S′系的洛仑兹变换，洛仑兹变换的传递性得证.不难发现，S′系相对于S系的速度为μ小于2u，正好否定了在相对时空观下伽利略变换的可行性.

4 结论

通过研究，有两个结论必须明确：一是，物理体系的状态据以变化的定律，同描述这些状态变化时的坐标系究竟是用两个在互相匀速运动着的坐标系中的哪一个并无关系.[2]二是，通过洛仑兹变换的矩阵形式和相对速度的角度，均证明洛仑兹变换具有传递性.当然，从群论出发的闭合定理[3]也证实了两个参照系转换叠加得到另外一个转换.

类比于光的波粒二象性在不同情况下有不同的体现，洛仑兹变换在传递过程中也有类似的情况.例如，S系与S′系过程中可以看作包涵有限或者无限个基于某一参数u的洛仑兹变换的叠加，若u足够小，S系与S′系之间的转换就趋于微分化多重甚至复杂化，而u越大直至等于S系与S′系的相对速度则两系之间的转换就变得整体但跨度大，而在实际生活信息传递应用中可以基于洛仑兹变换的传递性综合考虑上述结论的两个方面.

［1］关洪.再谈洛伦兹变换的推导[J].大学物理,2007(11):14-15.

［2］Zur Elektrodynamik bewegter Körper.Annalen der Physik,1905-6-30,17:891-921[Z].

［3］Е.М.栗弗席兹.场论[M].北京:人民教育出版社,1958:14-15.