基于随机规划理论的含异步风机的配电网故障重构

顾国华，秦永刚

(1.国电南瑞科技股份有限公司，江苏南京210061；2.新疆阿克苏市农一师电力公司输变电工区，新疆维吾尔自治区阿克苏843000)

随着用户对供电可靠性的要求的提高，研究如何在配电系统故障后正确快速地恢复供电，提高电网供电可靠性，具有重要意义。分布式电源（DG）的接入系统给传统配电系统潮流分布[1]、暂态稳定性[2]以及继电保护方式[3]等带来很大影响，其故障恢复与传统的单电源故障恢复有很大区别。对于传统配电系统的故障恢复方法已有较多研究，例如专家系统方法[4]、基于 Petri网的方法[5]、遗传算法[6，7]、粒子群算法[8]、禁忌搜索方法[9]等，但上述研究很少考虑配电系统中含异步风机等具有随机性和波动性功率输出的分布式电源接入情况。本文研究含分布式电源接入的配电网故障恢复问题，以异步风机为例，并假设在故障恢复时异步风机满足并网条件。由于风电机出力的随机性，需将风电场出力看作随机变量，利用随机规划理论中的机会约束规划来建立故障恢复模型，并用结合禁忌模因局部搜索的单亲遗传算法来求解优化模型。

1 风机模型

1.1 风机输出有功功率

对风速的大量实测数据表明，大部分时间里的风速都是比较平缓的，风速在0～25 m/s之间发生的概率较高。根据前人研究表明年平均风速可以采用威布尔分布函数来描述[10]。风电机的有功出力可以采用分段函数近似表示[11]：

式（1）中：vin，vrate，vout分别为切入风速、额定风速和切出风速。

1.2 风机模型

异步风力发电机的等效电路如图1所示[12]。

图1 异步电机等效电路

图1中，Xs为异步电机的定子电抗，Xr为异步电机的转子电抗，Xm为异步电机的励磁电抗，r2为异步电机转子电阻，s为滑差，P和Q分别为异步电机注入电网的有功和无功功率。实际注入电网的功率Pe、发电机吸收的无功Qe以及滑差s计算公式如下：

当异步风电机有功功率Pe确定时，其吸收的无功与节点电压和滑差s的大小有关。在进行含异步风电机的潮流计算时必须考虑风电机组本身的特性：异步发电机本身没有励磁装置，它要靠电网提供无功功率建立磁场，因此它没有电压调节能力，则不能简单将风机节点视为PQ节点。

在进行含异步风机潮流计算时，必须考虑风电机组的数学模型，将其扩展到系统的功率方程中，进行联立求解，或者将系统功率方程和风电机组方程交替求解，具体步骤如下[13]：

（1）已知风速，根据式（1）计算出异步电机有功出力Pe；

（2） 由 Pe和风电接入点电压 U（初始取 U＝1），根据式（3）计算出滑差 s；

（3）由Pe和滑差s根据式（4）计算异步电机吸收无功功率Qe；

（4）将风机等效成PQ（V）节点，利用常规潮流进行计算，得到风电场接入点电压U'；

（5） 如 U≠U'，令 U=0.5（U'+U），返回步骤（2）继续执行，直到2次计算电压满足收敛条件

2 基于随机规划理论的故障恢复模型

2.1 机会约束规划理论

在现实生活中，人们制定决策时常常会遇到不确定随机现象，用来描述随机现象的变量称为随机变量，含随机变量的数学优化问题称为随机规划问题。机会约束规划问题作为随机规划的一个重要分支，是由Charnes和Cooper首先提出来的，主要用来解决约束条件中含有随机变量的问题。对于含有随机变量的问题，考虑到所做决策在不利的情况下发生可能不满足约束条件情况，因此允许所做决策在一定程度上不满足约束条件，但是该决策应该使约束条件成立的概率不小于某一置信水平。带有随机变量的数学规划问题可以表示为[14]：

式（5）中：X为决策向量；ζ为一个随机向量；f为目标函数；gi为约束条件。但是由于随机变量的存在，目标函数（5）是没有准确意义的。

对于式（5），一种有意义的表达形式是如下的机会约束规划模型：

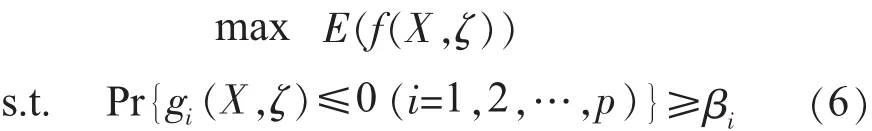
式（6）中：E（f（X，ζ））为（f（X，ζ））中事件的期望值，Pr中事件成立的概率，这是给定的约束条件成立的置信水平。

2.2 随机模拟技术

随机模拟又称为Monte-Carlo模拟，是一种实现随机系统抽样试验的技术，其技术是从给定的概率分布中抽取随机变量。估计事件发生概率：

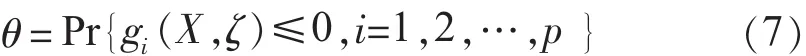
式（7）中：ζ为随机变量；φ（ζ）为其分布函数；gi（ζ）为函数实值。

上述事件发生概率θ，从随机变量概率分布中随机产生N个随机变量 ζi，i=1，2，…，N。 假设N次中共有N'个随机变量满足约束条件，根据大数定律，可以估算θ的值为：

2.3 目标函数

在传统的故障恢复研究的基础上，考虑异步风机的随机性，将随机规划理论应用到含异步风电机的配电网故障恢复研究中，建立的模型如下：

式（9）为网络损耗的期望值，式（10）为有功网损计算公式，式（11，12）是潮流等式约束，式（13，14）为线路有功无功概率约束条件，式（15，16）是电压幅值和相角概率约束。

2.4 约束条件的检验

以电压概率约束为例，对数学模型中的概率约束条件的处理采用下述方法：按照随机变量的分布函数随机生成规模为N的样本，这里是对于每种故障恢复方案生成风速样本v1，v2，…，vN，对于每一个样本分别进行潮流计算，检查是否满足约束条件，如果满足约束条件，计数器counter加1，在所有样本计算完以后判断counter/N≥β3是否成立，如果成立说明满足概率条件约束。从理论上来说，如果样本数足够多，模拟的结果也就足够精确，但是随着样本数的增加，计算量也大大增加，所以样本数的数目要根据实际情况设定。

3 故障重构模型的求解

3.1 基于禁忌模因局部搜索的单亲遗传算法

由于配电系统是“闭环结构，开环运行”，在实际运行中存在潜在的未闭合的环形结构，实际运行中只要保证这些潜在的环形网中有一个开关打开就可以保证配电系统的正常运行要求，因此在优化的时候可以将对应的环网看成一个整体，对其进行相关操作以保证优化的过程中满足配电系统的基本运行要求。根据这一特点，本文采用单亲遗传算法[15]进行优化，考虑到遗传算法在最优值附近时搜索最优解效率降低，引入模因理论的局部搜索最优策略，使算法快速全局收敛，为了避免重复的潮流计算，在单亲遗传算法中加入禁忌搜索。

3.2 模型求解

（1）基于环的染色体编码策略。系统中的开关只有2种状态，因此可以用二进制来编码，“0”代表开关断开，“1”代表开关闭合。编码时，利用配电网中“环”的结构特点，将隐含存在环中的支路编码放在同一个基因块中，为了保证得到的编码对应的配电网满足辐射状和无孤岛条件，需要满足每个基因块中仅有一个基因为“0”，其余基因全为“1”。如果某个公共支路同时存在于两个基因块中，还需要增加判定规则：若某一公共支路在两个基因块中编码同时为“0”，则此时的编码是不可行解。

（2）选择操作。在每次得到的群体中，首先根据群体的适应度大小进行顺序排列，然后用适应度最好的m个个体替代适应度最差的m个个体。在基因移位和基因突变过程中采用父子竞争的选择机制，即如果子个体的适应度优于父个体，则用子代替代父代，否则保留父代个体淘汰子代个体。

（3）移位操作。为了尽量保证染色体是可行解，移位操作是按照一定的概率选中一条染色体，然后把基因依次向后移一位，并把最后面的一个基因移到最前面的位置，其中移位的基因块的选择是随机的。

（4）突变操作。以一定的概率选定基因块，然后在确定的基因块中随机选定一位基因将其取反，即将基因“1”变为“0”，基因“0”变为“1”，在突变之后会产生 2个“0”或2个“1”，所以需要进行不可行解消除，若突变操作将“1”变为“0”，则将突变前为“0”的基因变为了“1”；若突变操作将“0”变为了“1”，则将其后相邻的基因变为“0”。

（5）模因局部搜索。在模因算法中，局部搜索策略被称为模因，通过模因作用于原始个体，产生由局部搜索策略搜索到新个体，并构成模因池。当需要局部搜索时，按照一定的方法从模因池中选择相应的模因，作用于局部搜索的个体产生新个体。本文采用的是定向型模因，对于故障恢复问题，即模因池中的染色体由原始个体相邻两个开关开或闭组合构成的。随着模型规模的增大，模因池中的模因也快速增加，为了加快搜索速度，这里采用部分贪心法从模因池中选择模因作用于原始个体，当有一个模因作用于原始个体，使个体质量有所提高，就用该个体取代原始个体，不再进行搜索。

（6）禁忌搜索。对于每一种恢复策略，需对产生的样本风速分别进行潮流计算，重复潮流计算使运算量大大增加。为避免重复计算，引入禁忌搜索，即将搜索到的恢复方案和适应度加入到禁忌表中，在下一次重新生成染色体时，首先对禁忌表进行搜索，如果该染色体已经在禁忌表中，直接从禁忌表中调用适应度函数，否则计算适应度并将染色体和适应度加到禁忌表中。

（7）算法流程图如图2所示。

图2 算法流程图

4 算例分析

本文采用IEEE33节点测试算例，其网络结构如图3所示。

图3 系统结构图

图3中实线为普通支路，虚线为联络开关支路，初始状态时，联络开关是打开的，节点10接入异步风电机。某一时刻支路7-8发生故障退出运行，假设在故障后风机满足并网条件，采用本文研究模型对该故障情况进行故障恢复。风机参数和运行数据如表1所示。

无异步风机以及含异步风机时的故障恢复结果如表2所示。其中“恢复策略（打开开关）”表示将所有开关包括联络开关都合上的假设前提下，故障恢复策略给出打开开关的集合。可以看出，故障恢复后，配电系统中接入异步风机比没有接入异步风机的情况系统网损偏小，说明在配电系统中接入分布式电源可以改变潮流分布，优化源荷分布配置，减少系统网损。

表1 风机参数与运行数据

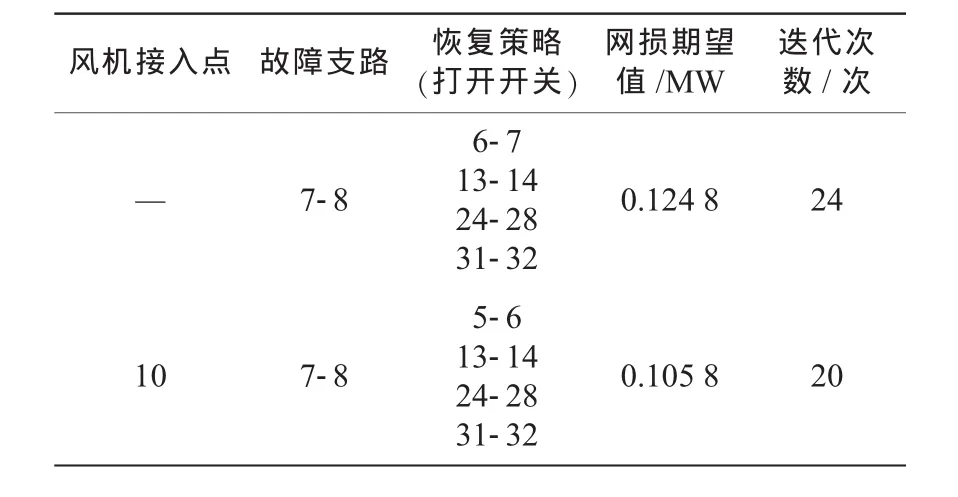
表2 故障恢复策略

迭代过程中的最小适应度和平均适应度曲线如图4所示。

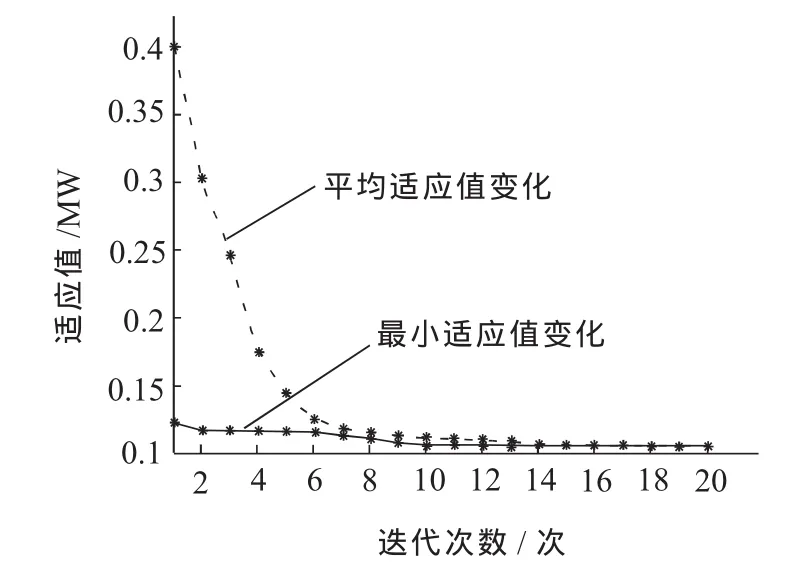
图4 风机在节点8时适应度曲线图

从曲线图可以看出，本文所应用的优化方法具有较好的收敛性。

5 结束语

本文计及了风电的随机性，将风机有功出力作为随机变量考虑，利用随机规划理论建立了含异步风机的配电网故障恢复重构，充分考虑了风电不确定给配电网故障恢复带来的影响。通过研究发现，直接接入配电网的分布式电源，例如异步风机可有效地减少系统的网损值，使系统具有更好的经济性；在单亲遗传算法中采用基于模因的局部搜索和禁忌搜索，加强了算法搜索最优解的能力并且避免了大量的重复工作。

[1]代 江，王 韶，祝金锋.含分布式电源的弱环配电网络潮流计算[J].电力系统保护与控制，2011，39(10)：37-41.

[2]BARKER P P,De MELLO R W.Determining the Impact of Distributed Generation on Power System,Part I:Radial Distribution Systems[C].Proceedings of 2000 IEEE Power Engineering Society Summer Meeting,2000.

[3]孙景钌，李永丽，李盛伟，等.含分布式电源电网保护方案[J].电力系统自动化，2009，33(1)：81-84.

[4]KRISCHEN S,VOLKMANN T L.Restoring Power System with an Expert System[J].IEEE Trans.on Power Systems,1991,06(2):558-564.

[5]WU J S,LIU C C.A Petri net Algorithm for Scheduling of Generic Restoration Actions[J].IEEE Trans.on Power System,1977,12(1):69-76.

[6]梁 勇，张 焰，侯志俭.遗传算法在配电网重构中的应用[J].电力系统及其自动化学报.1998，10(4)：29-34.

[7]唐 斌，罗 安，王 击.改进遗传算法的编码策略及其在配电网重构中的应用[J].继电器，2004，32(13)：35-39.

[8]余贻鑫，段 刚.基于最短路算法和遗传算法的配电网络重构[J].中国电机工程报，2000，20(9)：42-49.

[9]盛四清，梁志瑞，张文勤，等.基于遗传算法的地区电网停电恢复[J].电力系统自动化，2011，25(16)：53-55.

[10]BOWDEN G J,BARKER P R,SHESTOPAL V O,et al.The Weibull Distribution Function and Wind Power Statistics[J].Wind Engineering,1983（7）:85-89.

[11]丁 明，吴义纯，张立军.风电场风速概率分布参数计算方法的研究[J].中国电机工程学报，2005，25(10)：107-110.

[12]FEIJOO A E,CIDRAS J.Modeling of Wind Farms in the Load Flow Analysis[J].IEEE Trans.on Power Systems,2002,15(1):110-115.

[13]吴俊玲，周双喜，孙建锋，等.并网风力发电场的最大注入功率分析[J].电网技术，2004，28(20)：28-32.

[14]刘宝碇，赵瑞清.随机规划理论与模糊控制[M].北京：清华大学出版社，1998.

[15]张利民，马 强，李振坤，等.基于禁忌克隆遗传算法的配电网故障恢复重构[J].电力系统及其自动化学报.2010，22(1)：60-64.