基于融合算法的沉降监测数据反馈分析

李红波

（中船勘察设计研究院有限公司，上海 200063）

基于融合算法的沉降监测数据反馈分析

李红波

（中船勘察设计研究院有限公司，上海 200063）

沉降变形是安全监测的重要内容。基于分布式多源数据智能融合算法，具有良好的修正性和互补性，可解决传感器测量范围局限与失准及其数据误差。某跨海大桥群桩基础沉降监测的应用结果表明，该方法具有较高可靠性和识别精度，为安全监测与分析提供了新的有效手段。

沉降监测；数据处理；反馈分析；融合算法

近年来，随着岸带经济圈的崛起，沿海工程迅速发展，而由于地质环境的复杂性，海上建筑物的基础安全成为规划、建设和管理必须面对与处置的重要问题。安全监测是反映其与海洋地质条件适应性的重要评价内容，健全和完善监测网络系统、采用自动化监测技术、完善地质信息平台、提高风险识别预警能力是重要途径之一。

沉降变形监测是评价桩基础的一项重要指标，但是海洋建筑物尤其是超大群桩基础的沉降变化，受潮位、波浪、日照辐射等环境因素和偶然因素的影响，可导致观测数据序列呈现异常过程，且这些环境因素不仅只影响某个测点，还会造成观测系统出现异常群，从而严重干扰桩基础工程特性的分析和预测。更重要的是，异常过程和异常群往往很难利用普通技术进行识别和剔除。此外，不同类型的传感器，因其精度、安装方式和埋设位置不同，而使数据及其噪声的特性存在差异。故有必要采用信噪分离技术剥离各种噪声的影响，并根据不同类型传感器观测结果的可信度和重要性，进行多传感器数据融合。

对于监测数据降噪，国内外许多学者开展了大量研究，尤其是基于“软计算”方法的修正数据得到广泛应用。Mallat提出多分辨分析的概念，使小波具有带通滤波特性，从而可以利用小波分解与重构的方法滤波降噪[1]。田胜利等利用小波去噪技术，对一组建筑物变形监测数据进行去噪处理，表明该方法能够识别观测噪声和有用信息[2]。然而实测信号往往伴随冲击信号，从而限制了单一去噪方法的适用性。石双忠等提出一种基于小波消噪时序分析改进法[3]。潘国荣等采用把小波变换与神经网络有机结合的小波神经网络法[4]。但小波神经网络法还存在结构优化问题，其收敛速度、鲁棒性和预测精度还有待进一步提高。

20 世纪60 年代初，Kalman 等提出递推式滤波算法。它是一种对动态系统进行实时数据处理的有效方法，可实现对各种原始监测数据的异常干扰进行滤波处理，同时有效提高判定精度。何亮等通过采用离散Kalman 滤波估计和小波分析相结合的方法，建立了可应用于结构健康监测的离散时间动态模型[5]。王利等提出用Kalman 滤波法先对原始变形监测数据进行滤波处理，而后再建立GM 模型进行灰色预测，并用实例证实了该法的有效性[6]。但无论是数据降噪还是数据融合，在深水群桩基础整体沉降分析中的应用研究仍较少见。

在多点监测中，传统的分析方法往往集中在对某一个传感器采集的数据进行分析判断，这首先要求合理选取“关键点”，而该点的选取受人为影响因素较大；其次，该点是否具有代表性亦无法准确验证，无法避免以偏概全；最后，该点的选取必须经过大量的现场工作和研究，但是受工程条件和时间限制，显然不易完成。而采取多个指标分别进行评判，很难准确判断出桩基的整体工作状态，这是因为各个监测点受到的外界影响不一致，如日照、波浪、温度和潮位条件等，容易引起分析系统出现紊乱，从而严重干扰桩基础沉降量和桥基安全的综合分析和预测。因此如何将各传感器采集的数据进行综合有效融合和提取，需要进一步研究[7,8]。

已有研究表明，分布式融合算法能够有效融合监测数据[9]，其中Kalman滤波算法是其核心技术，监测过程可视为对每一个传感器运动轨迹的监测。根据量测值提取目标的综合信息，实质是建立多个固定的状态方程和量测方程来描述桩基沉降量，并对各监测点采集到的数据进行跟踪滤波去噪，以获得被监测对象的整体工程特性。

1 桩基沉降时间序列监测模型

为便于数学描述，对于每一个传感器监测点，其沉降量可用下述方程组进行描述：

其中，a(x)表示监测点在x时刻到x+1时刻的加速度，v(x)表示桩基在x时刻的速度，s(x)表示桩基在x时刻的位置。a(x)是服从零均值、方差为Q的正态分布的噪声序列，且a(x)和a(y)(x≠y) 互不相关，即，其中δ是克罗内克函数，其特性为k=1时，δ(k)=0；k=0时，δ(k)=1。

由以上分析可建立桩基在沉降阶段的时间序列动态监测模型：

式中：

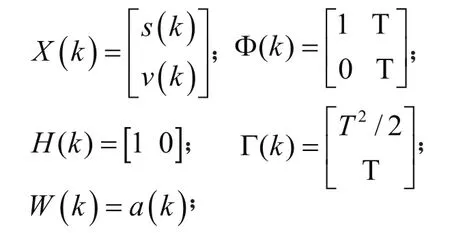
Z(k)为桩基的实际沉降量监测值，v(k)是均值为零、方差为Q的量测噪声序列，且与W(k)不相关[10]。

2 分布式多传感器数据融合

分布式多传感器数据融合是一种决策级融合方法，通过一系列的数据关联和互补，能够最大限度地改正错误，使误差达到最小，从而避免误差延续造成结果不精确。在桩基的沉降量监测中，由于各个监测点在单位采样时间内沉降量都是唯一的且反映了桩基的变形，因此各传感器产生的沉降量是相关的，可采用有反馈信息结构的卡尔曼滤波进行融合计算。

有反馈信息的分布式融合结构[11]，是指在数据处理前后均要进行卡尔曼滤波的修正，即有一个数据信息反馈沟通的过程，最后才能进行融合计算，融合计算方法如下[12]：

3 工程应用实例

3.1 工程概况

东部某跨海大桥8号索塔塔墩采用了“超深、大直径、桩距与桩径比小”的群桩基础，由于该桩基础位于海中，且属于高桩，上部裸露于海水中，故在其中上部布设了不锈钢护筒；同时考虑到地震影响及水平承载力提高的需求，钢护筒通常被永久保留为桩基础的受力结构。该结构的主要特征是受力复杂，外界影响因素较多，尤其是潮汐作用和复合群桩影响效应。由于自然条件限制，其量化影响程度无法精确计算出。为此，基于广角度多源监测理念，开展了多项自动化原位跟踪监测，内容包括压力、轴力、承台受力状态、基桩弯曲变形、沉降量等， 由于监测位置及桩身材料不同，对沉降量的监测，采用了不同类型的传感器。在该群桩基础施工时期一共布置了10个自动化采集点，均布于最外侧的桩身。观测时间开始于桩基础施工完成，并一直延续至今。由于日照、潮水冲刷等原因，2008年7月和2010年11月，分别有2个传感器失效，始终处于正常工作状态的有8个。近年来，该桩基沉降量出现了个别传感器测量的沉降量有反复变化的现象，且传感器间采集的数据有矛盾等值得关注的问题。

3.2 融合结果及分析

以2007～2012年桩基沉降量实测数据为研究对象，起始点选在2007年1月1日，并将其赋值为0，历年12月31日与起始点的总差值作为数据融合前的值，建立桩基沉降量的时间序列，进行数据融合分析，以判断整个超大群桩基础的沉降值。

由2007～2012年间8号索塔各沉降传感器采集的监测值可知（表1），该群桩基础在监测时间内大部分传感器采集的沉降量数据均随时间推移有增大趋势。自监测以来，最大沉降量发生在监测点S8-4，沉降量达81.9mm；最小沉降量发生在监测点S8-1，沉降量为62.5mm；年间最大沉降量变幅发生在2007～2008年的监测点S8-5，沉降量达41.2mm；年间最小沉降量变幅发生在2010～2011年的监测点S8-6，沉降量仅有2mm。但不难看出，S8-7在2007～2011年间，其沉降量随时间有增大趋势，但2011年间以来，却发生了“回弹”；同样，S8-8在2007～2010年间，沉降量为增大趋势，但2010～2011年间也有“回弹”，而2011～2012年间又呈增大趋势。同时，还有个别传感器采集的数据具有“跳跃性”，具体表现在反复无规律的变化趋势，即出现同一时期各个监测点的指标对桩基整体沉降的评价出现不一致的现象，如图1所示。

表1 沉降量实测及融合处理值 (mm)Table 1 The actual measurement and the fusion value of subsidence

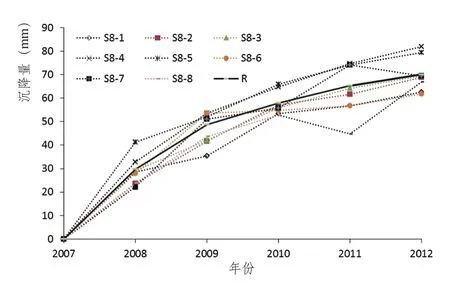
图1 沉降量实测值与融合值变化曲线Fig.1 The changing curve of actual measurement and the fusion value of subsidence

分析此现象，其原因是由于采用的不同类型传感器的精度存在偏差，加之传感器分布位置也有差异，引起数据矛盾，进而引发数据间的冗余性[13]。为了消除这种矛盾性，根据传感器分布特征，采用分布式多源数据融合处理方法进行融合，融合结果见表1。

对比图表可知，融合后的数据首先消除了传感器采集数据的矛盾性，可修正融合前数据的冗余性和不准确性，获得了被测对象的一致性描述和解释。采用具有反馈式融合方法后，去除了某些传感器数据的反复无规律现象，在总体上降低了数据的矛盾性，这是因为每个传感器的误差是不相关的，融合处理后可抑制误差。

其次，融合后的数据值处于各传感器采集的数据之间，接近该时间内分布较多的数值，符合正态分布，这是因为研究对象为整个桩基平台的沉降量，该融合方法具有良好的修正性和互补性。这种修正性和互补性，可以补偿单一传感器的不准确性和测量范围的局限性，这样也就纠正了数据误差，消除了“回弹”现象，同时也改正了个别传感器采集数据的“跳跃性”。

综上所述，融合后的数据比原始采集数据的子集具有更优良的兼容性，即融合后的效果更加理想。融合后的值可以作为评价群桩基础的“关键点”，其首先不受人为影响因素的控制；其次具有良好的代表性；最后，其不需要进行大量的现场试验，能够节省成本，降低风险。

就实际情况而言，桩基在投入使用时，对周围环境有一个适应过程；大桥运行一段时间后，桩基才趋于稳定。其沉降量变化表现出一种由大变小的趋势，显然，融合后的数据更加符合这一规律。

4 结论

（1）分布式融合算法能够有效融合大桥群桩基础沉降量的监测数据，文中采用的卡尔曼滤波算法是其核心技术，监测过程可视为对每一个传感器运动轨迹的监测，根据量测值提取目标的综合信息，建立的多个固定的状态方程和量测方程来描述桩基沉降量是可行的；对各监测点采集到的数据进行跟踪滤波去噪是有效的，能够获得被监测对象的整体工程特性。证明基于卡尔曼滤波融合算法，可应用于大桥群桩桩基沉降监测数据综合信息的提取。

（2）分布式融合算法，充分利用各个监测点采集的数据，获得了被测对象的一致性描述和解释，消除了融合前数据的矛盾性和冗余性，发挥了数据的互补性，而且符合一般工程特性和沉降量变化规律，结果较为理想。

（3）传感器数量越多，越能提高系统的可靠性。一方面可以增加数据间的互补性，另一方面当某个或某几个传感器失效时，系统仍能正常运行。该融合方法还可以将河床冲刷、桩顶轴力、基桩轴力、桩底土压力、承台受力状态、基桩弯曲变形等一系列不同类型的传感器采集的数据进行综合评判，应用面较广。

References)

[1] Mallat S G. A theory for multiresolution signal decomposition: the wavelet representation[J].Pattern Analysis and Machine Intelligence, 1989,11(7):674-693.

[2] 田胜利,周拥军,葛修润,等. 基于小波分解的建筑物变形监测数据处理[J]. 岩石力学与工程学报,2004,23(15):2639-2642.

Tian S L, Zhou Y J, Ge X R, et al. Processing of monitoring data of building deformation based on wavelet transform[J].Chinese Journal of Rock Mechanics and Engineering, 2004,23(15):2639-2642.

[3] 石双忠,岳东杰. 基于小波消噪技术的时序分析法用于GPS 监测数据处理[J]. 现代测绘,2006,29(4):17-19.

Shi S Z, Yue D J. Application of time-series analysis based on wavelet to GPS deformation monitoring data-processing[J].Modern Surveying and Mapping,2006,29(4):17-19.

[4] 潘国荣,谷川. 变形监测数据的小波神经网络预测方法[J]. 大地测量与地球动力学,2007,27(4):47-50.

Pan G R, Gu C. Wavelet neural network prediction method of deformation monitoring data[J].Journal of Geodesy and Geodynamics,2007,27(4):47-50.

[5] 何亮,敖鹏,孙炳楠. 结构健康监测信息的多尺度分析[J]. 市政技术,2006,24(3):182-186.

He L, Ao P, Sun B N. Analysis of information in multiple measures for structure health monitoring[J].Municipal Engineering Technology, 2006,24(3):182-186.

[6] 王利,张勤,刘万林. 基于卡尔曼滤波的GM 模型及其在公路边坡变形预测中的应用[J]. 工程勘察,2007,(3):56-59.

Wang L, Zhang Q, Liu W L. Application of Kalman filter based on GM model to road slop deformation monitoring[J].Engineering Investigation,2007, (3):56-59.

[7] Hall D L. Mathematical techniques in multi sensor data fusion[M]. Artech House, London, 1992.

[8] Waltz E, Llinas J. Multisenser data fusion[M]. New York: Artech House, Inc., 1990.

[9] 苏怀智,顾冲时,吴中如. 大坝工作性态的模糊可拓评估模型及应用[J]. 岩土力学,2006,27(12):2115-2121.

Su H Z, Gu C S, Wu Z R. Assessment model of dam behavior with fuzzy extension theory and its application[J].Rock and Soil Mechanics,2006,27(12):2115-2121.

[10] 涂国平,邓群钊. 多传感器数据的统计融合方法 [J]. 传感器技术,2007,20(3),28-32.

Tu G P, Deng Q Z. A statistical method for the data fusion of multisensor[J].Journal of Transducer Technology,2007,20(3):28-32.

[11] 郭科,彭继兵,许强,等. 滑坡多点数据融合中的多传感器目标跟踪技术应用[J]. 岩土力学,2006, 27(3):479-481.

Guo K, Peng J B, Xu Q, et al. Landslide multi-point multisensor data fusion target tracking technology[J].Rock and Soil Mechanics,2006,27(3):479-481.

[12] Singer R A, Sea R G, Housewright K. Derivation and evaluation of improved tracking filters for use in dense multi sensor environments[J].Information Theory,1974,20(4):423-432.

[13] Shalom B Y, Tse E. Tracking in a cluttered environment with Probabilistic data association[J].Automatic,2005,11(5):451-460.

Feedback Analysis of Subsidence Monitoring Based on Data Fusion Algorithm

LI Hong-Bo
(China Shipbuilding Industry Institute of the Engineering Investigation & Design Co, Ltd, Shanghai 200063, China)

Subsidence deformation is an important index of safety monitoring. The fusion algorithm with the distributed intelligent multi-source data can be the good correction and complementarity, and solve the sensor measuring range limitation and its misalignment and data error. The piles group foundation subsidence monitoring results from a bridge cross the sea show that it is a good method with higher reliability and recognition precision and provides a new effective measure for safety monitoring and analysis.

subsidence monitoring; data processing; feedback analysis; fusion algorithm

P229.5

A

2095-1329(2013)02-0084-04

10.3969/j.issn.2095-1329.2013.02.020

2013-05-27

2013-06-17

李红波(1967-),女,高级工程师,主要从事岩土工程勘察与设计研究.

电子邮箱：lhb2150607@126.com

联系电话：021-62548041×8663