滚切式横切剪剪切机构分析
2013-04-09贾祎晶蔡金龙
贾祎晶,蔡金龙
(大连华锐重工集团股份有限公司,辽宁 大连 116013)
0 前言
滚切式横切剪用于在冷状态下对钢板进行切头切尾、剪切试样、分段及定尺横向剪切。主要剪切的钢种为高强度机械工程用钢、优质碳素结构钢等。最常见剪切机构为二轴二偏心式,由两根曲柄和连杆、导向杆、弧形上刀体及平直下刀体组成(见图1)。
由于两根曲轴的转速及转向相同,但相位角不同,因此,工作时弧形上剪刃的左端先下降,直到与下剪刃左端相切,再沿下剪刃滚切,当滚切到与下剪刃右端相切时,剪切完成。整个剪切过程中钢板几乎不发生弯曲,使得板材切口光滑、无变形、设备能耗小、剪刃寿命长、产量高。

图1 滚切式横切剪剪切机构简图Fig.1 Schematic diagram of mechanism for roll-cut crosscut shearing
剪刃重叠量的均匀度是钢板剪切质量的重要影响因素,而剪切角是影响剪切力的最主要因素。因此,在设计滚切式横切剪设备时,有必要对滚切剪剪切机构进行运动学计算,并对计算结果进行优化。
1 剪切机剪切过程
滚切式横切剪的剪切过程用图2 所示的5 个位置表示。安装圆弧形上刀刃的上刀架由两个偏心半径相同、转向相同、转速相同、偏心相位角不同的偏心轴带动。位置1为上剪刃的起始位置,两个偏心轴转动,圆弧剪刃的出口端(图示左端)首先下降,另一端相差一个相位下降,直到前缘(图示左端)下降到与下剪刃相切,即位置2,然后,上剪刃沿假想线滚动。位置4 是上剪刃滚动到与假想中部相切,一直到入口端(图示右端)相切,即位置5,之后升起恢复到原位置1,完成一次剪切。

图2 滚切式横切剪的剪切过程Fig.2 Process of roll-cut crosscut shearing
2 剪切机构运动分析
建立机架上的固定坐标系 和上刀体平面上的活动坐标系,各杆的矢量位置如图3 所示。
图3 中,以某厂产品为例,确定机构的尺寸参数为


图3 滚切机构矢量图Fig.3 Vector diagram of roll-cut mechanism

2.1 位置分析
滚切式横切剪的剪切机构为平面七杆机构,由闭环HGDEFKH 和闭环HGCBAFKH组成,针对每一闭环,列出闭环矢量方程:
将闭环矢量方程以复数形式表示为:
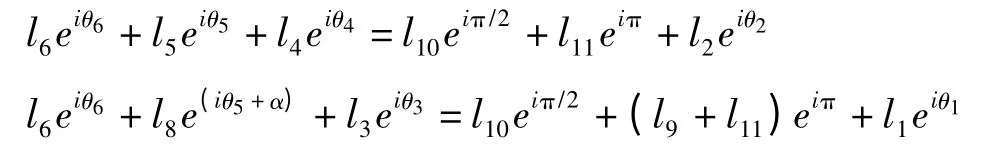
用欧拉公式展开,可得到方程:

式(3)、(4)包括四个实数方程,其中:l1到l11以及α 均为已知量,且由于输入杆AB 以及FE为等速同向且相位差为54°的回转运动,所以:θ2=θ1-54°。通过Matlab 软件,给出θ1的一系列离散值,求出θ2~θ6。
2.2 速度分析
AB 与FE 均以匀速ω6同步转动,分别将方程(3)以及(4)对时间t 求导:

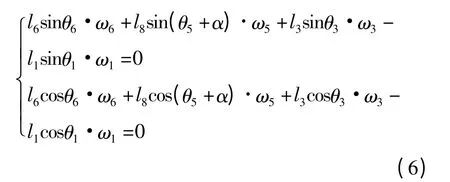
由式(5)和(6)可以解出ω3,ω4,ω5,ω6与ω1的关系式,其中ω5描述了上剪刃的角速度。
2.3 上剪刃动态最低点的运动轨迹分析
剪刃的动态最低点k 点的坐标,可根据它与剪刃中点h 的几何关系(如图4)来求解。

式中,β为上刀架倾角,可以表示为θ5- θ50,(θ50为θ5的初始角度,参见图3)。

图4 k 点与h 点的几何关系Fig.4 Geometrical relationship between k point and h point
剪刃中点h 在动坐标系中的坐标为

通过坐标变换,求出其在固定坐标系H-xy中的坐标为
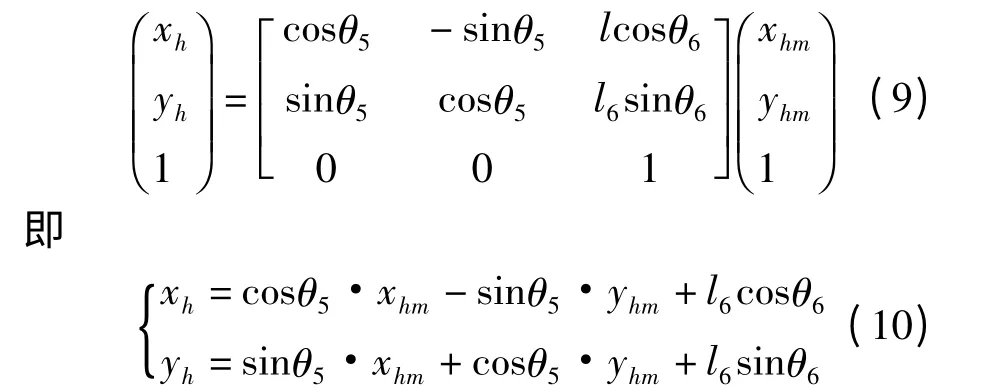
因此,剪刃的动态最低点k 在固定坐标系H-xy中的坐标为:

应用MATLAB 求出一系列位置时剪刃动态最低点坐标如图5。
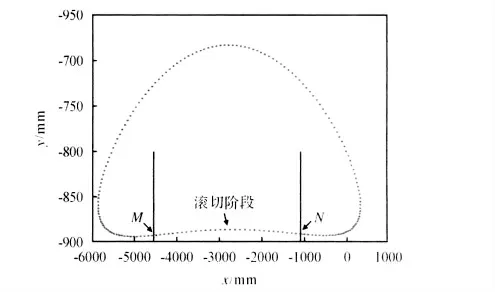
图5 上剪刃动态最低点k 的运动轨迹Fig.5 Motion track of dynamic lowest point k of upper blade
由图5 可以看出,剪刃动态最低点k 的运动轨迹的下半部分是一条近似直线,上剪刃在剪切过程中就在这条直线上滚动。若设计上剪刃的弧长,使得刚进入近似直线段和退出近似直线段的剪刃上动态最低点分别为剪刃圆弧的两个端点,则能实现最大剪切宽度。以某厂产品为列:横切剪的剪刃圆弧段为MN 段,其中M 点在滚切剪工作过程中的最低点坐标为ML:(-4533.4,-892.9959),N 点的最低点坐标为:NL:(-1053.3,-890.9465),即上剪刃在ML点处开始沿滚切线作滚动剪切,到NL点处退出滚动剪切。ML到NL的长度3.48 m 可看作该滚切剪可剪切的最大钢板宽度Bmax。
若将曲轴旋转360°等分为180 个离散点,即从位置1 到位置180,曲轴对应的旋转角度为2°到360°,第 个位置旋转的角度为2i。
由动态最低点的轨迹曲线可以得到,当i=75时,上剪刃弧段左端点M 到达最低点,滚切剪开始进入沿下剪刃滚切阶段,当i=107 时,上剪刃弧段右端点到达最低点,接着,滚切剪开始退出沿下剪刃滚切阶段。因此可以得到上刀刃作沿下刀刃滚动剪切段对应曲轴转角θ1的范围为:θ1∈[117+150,117+214]=[267°,331°]。
理想状态下,在滚动剪切时,动态最低点的轨迹是一条水平的直线。这条近似直线与参考水平线的偏差就反映了剪刃重叠量沿剪刃宽度方向上的变化。剪刃重叠量的均匀度是钢板剪切质量的重要影响因素,因此,可以通过结构参数优化来提高剪刃重叠量的均匀度,从而提高钢板的剪切质量。
取出剪刃动态最低点k 运动轨迹在滚切阶段的近似直线段作为研究对象,并将y 轴坐标放大,如图6 所示。

图6 剪刃动态最低点k 运动轨迹中的近似直线段Fig.6 Approximate straight line in motion track of blade dynamic lowest point k
通过最小二乘法,并且规定拟合直线斜率为0(MATLAB 中的具体代码为polyfit(xk,yk,0)),拟合出来的直线为(见图7),即可以认为在剪切阶段,上剪刃的最低点保持在 的位置。通过这个数据来调整下刀刃的位置,以保证所需要的剪刃重叠量,从而保证钢板的剪切质量。以某厂设备为列,为保证5 mm 的重叠量,可以设置下刀刃的高度为:-888.174 +5=-883.174。

图7 最小二乘法拟合上剪刃动态最低点Fig.7 Upper blade dynamic lowest point interpolated by least-squares method
求出上面一系列位置y 方向坐标与平均值的标准差为:

σ 值越小,说明y 方向坐标值越集中在平均值上下,也就是上下剪刃重叠量沿剪刃长度方向上越均匀,钢板剪切质量越好;反之则否。
另外,通过MATLAB 程序求出的上刀架倾角β 在一个周期内的变化曲线如图8 所示。

图8 上刀架倾角变化曲线Fig.8 Curve for tilt angle of upper blade frame
根据横切剪的剪切工艺,在滚动剪切过程中,需要上剪刃相对于钢板切面的相对滑移量较小,保证钢板断面整齐、无台阶、无变形,从而提高剪切质量,并且减小刀片的划伤和磨损。这就要求上剪刃在滚切阶段的运动为纯滚动,由于上剪刃圆弧半径很大,因此在剪切过程中,上剪刃圆弧中点横坐标几乎保持不变。但是,从图9可以看到,上剪刃中点h 横坐标在保持一段不变后(10 个离散点位置,即20°),开始逐渐减小,可见,横切剪剪切机构在滚切初期,上剪刃能够保证作纯滚动,随后,上剪刃开始有向左的滑移,最大滑移总量接近6 mm。上剪刃中点h 横坐标与曲轴旋转角度关系如图10 所示。
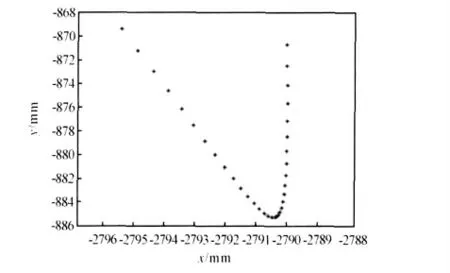
图9 上剪刃中点h 在固定坐标系下的运动轨迹Fig.9 Motion track of upper blade midpoint h in fixed coordinate
2.4 剪切角变化分析
圆弧滚切剪由于上剪刃的圆弧半径很大,它和钢板接触点处的切线与直线形下剪刃之间的夹角即是剪刃倾角,也就是滚切角,即图11 中的α。由于在滚动期间,上剪刃沿下剪刃基本是纯滚动,因此,滚切角略有变化,但基本恒定。由图11 中的几何关系,得剪切角

图10 上剪刃中点h 横坐标与曲轴旋转角度关系Fig.10 Horizontal coordinate of upper blade midpoint h versus crankshaft rotational angle


图11 滚切时的剪切角Fig.11 Shearing angle in process of roll-cut
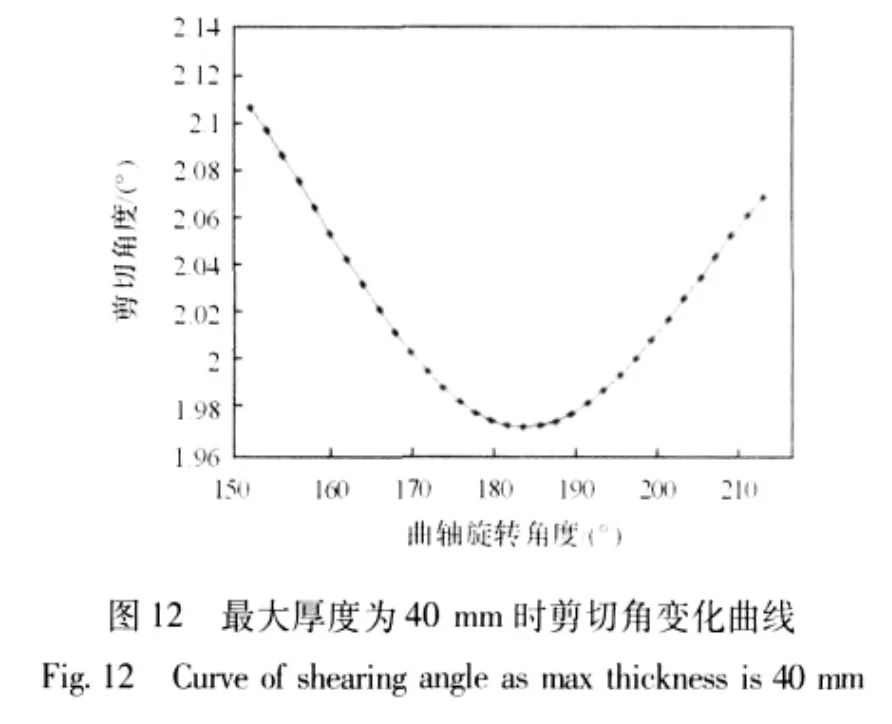
通过MATLAB 程序可分别求出剪切钢板厚度为40 mm 和50 mm 时,不同位置的剪切角变化曲线如图12 和图13 所示。
剪切钢板最大厚度为40 mm 时,由剪切角的变化曲线可以看出,在剪切阶段剪切角在2.04°左右波动。
剪切钢板最大厚度为50 mm 时,由剪切角的变化曲线可以看出,在剪切阶段剪切角在2.25°左右波动。
3 结论
通过对剪切机构运动学计算,并通过对剪切机构各连杆长度的调整,使其运动轨迹得以优化,可得到如下结论:
(1)在剪切阶段,沿剪刃长度方向,应尽量使上剪刃的最低点保持在某一直线位置,通过调整下刀刃的位置,使上下剪刃重叠量沿剪刃长度方向平均差值最小,钢板剪切质量越好;反之则否。

(2)横切剪剪切机构在滚切初期,应尽量使上剪刃能够保证作纯滚动,随后,上剪刃开始有向左的滑移。即在曲轴旋转20°范围内,可以保证钢板断面整齐、无台阶、无变形,剪切质量最佳,并且减小刀片的划伤和磨损。
(3)在滚动期间,上剪刃沿下剪刃基本是纯滚动,应尽量控制滚切角的变化范围,这可以避免剪切过程中尖峰载荷的出现,使剪切更平衡,剪刃磨损更小,寿命更长。
[1]马立峰,黄庆学.新型滚切剪空间剪切机构优化数学模型的建立及应用[J].四川大学学报,2008(2).
[2]马立峰,黄庆学.新型钢板滚切剪剪切机构运动学分析[J].工程设计学报,2007(5).
[3]黄庆学,马立峰.新型滚切剪非对称曲柄机构原理[J].机械工程学报,2008(5).
[4]孙复森,杨惠新.滚切式横切剪机构参数优化研究[J].冶金设备,2008(4).
[5]李雷生,秦立学.滚切剪特点及关键参数分析[J].Science & technology information.2008(24).
[6]王德春,姜长平.滚切剪剪切力的实验研究[J].重型机械,1997(6).
