多负载非接触电能传输系统传输效率方程

方群芳， 牛王强

(上海海事大学 科学研究院，上海 201306)

0 引 言

非接触电能传输(Contactless Power Transfer，CPT)是一项新的电能传输技术，其发送和接收机构可以自由分开，用电设备以非接触方式从固定电网中获取电能.耦合模理论(Coupled-Mode Theory, CMT)是研究两个或多个电磁波模式间耦合的一般规律的理论，近年来麻省理工学院的物理学家将CMT用于CPT系统的计算，以降低多线圈耦合电路计算的复杂性.KURS等[1]在磁共振系统中用CMT分析距离与效率的关系.刘志军等[2]从电路方面分析多负载系统的效率和补偿电容的选择方法，提高传输效率.夏晨阳[3]给出适用于 CPT系统谐振耦合机构效率计算的一般公式，简化CPT系统效率的求解过程.赵彪等[4]和傅文珍等[5]也从电路方面指出在谐振频率下CPT系统传输效率最大.杨明生等[6]和谢卫等[7]对主电路拓扑结构进行深入研究，用电路理论(Circuit Theory, CT)推导出不同漏感补偿拓扑下的补偿参数.IMURA等[8]和KARALIS等[9]用电路方法分析CPT系统在不同距离下传输效率和耦合系数的变化，得出在不同距离下传输效率的变化规律.

以上学者仅仅用一种方法对CPT系统进行分析，接下来介绍用CMT和CT两种方法分析的工作.刘宿城等[10]在磁共振中用两种方法分析得出最佳的工作频率就是谐振点，另外还表明CMT更适合描述谐振耦合状态下系统能量的变化，并将两种方法进行对比.牛王强等[11-12]用CMT和CT对比分析频率的分裂现象，给出分裂频率公式.KIANI等[13]用两种理论分析在同一轴线上n个线圈中继系统的效率问题，得到中继无线电能传输系统CMT下的效率计算公式与CT下的计算公式完全等效.本文将美国学者的工作推进到多负载系统，指出在系统的谐振频率处，多负载CPT系统CMT下的效率计算公式与CT下的计算公式完全等效，并进一步对单负载和双负载的结论进行物理验证.

本文仅分析稳态特性.首先用CT的思想解决两个线圈的能量传输效率问题，然后通过CMT得出两个线圈感应连接的能量传输效率方程，将两个方程对比后发现可以变换为一套相同的公式.随后分析3个线圈、4个线圈、一直到n-1个线圈都可以变换为同一套公式，最后给出两个线圈和3个线圈的物理实验结果，结果表明CT和CMT在估算能量传输效率方面的一致性.

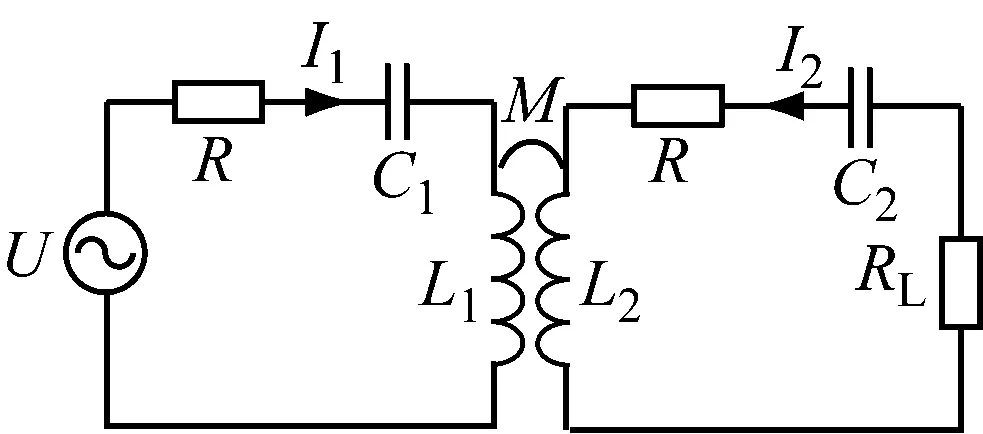
图1 单负载线圈的CPT拓扑结构

1 单负载的电路分析

1.1 电路分析

(1)

(2)

(3)

(4)

(5)

1.2 CMT分析

CPT系统分析中，常常只涉及稳态分析，在此也仅分析稳态特性.主线圈的幅值在正弦时为一个常数；同理，次线圈的幅值也是一个常数，两个时间域线圈a1(t)，a2(t)的原始储能可分别表示为|a1(t)|2，|a2(t)|2.由CMT[8-9]可得

(6)

(7)

在上述两式中，Γ1，Γ2，ΓL分别为原线圈的损耗、负载线圈的损耗和负载的吸收功率，K12为两个线圈的耦合率，Fs(t)为励磁损耗(忽略不计).CMT中，a1(t)=A1e-jωt，a2(t)=A2e-jωt都是正弦信号；P1=2Γ1|A1|2，P2=2Γ2A2|2和PL=2ΓL|A2|2分别为原线圈、副线圈和负载的功率.由能量守恒定律可得

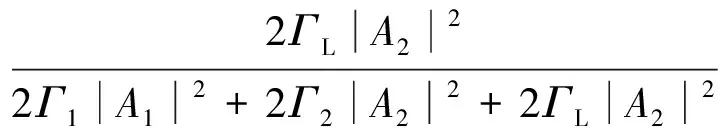
(8)

(9)

与式(5)对比可知，两种方法求出的传输效率的表达式相同.

2 两个负载电路的传输效率分析

2.1 电路分析

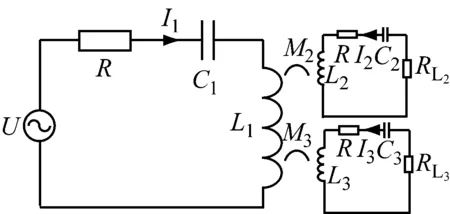
图2 两个负载线圈的CPT拓扑结构

对于图2电路，M2和M3为L1分别与L2和L3的互感，RL2为线圈2所带的负载，RL3为线圈3所带的负载，K2和K3分别为两个负载线圈的耦合系数.同理可得

(10)

(11)

(12)

在谐振状态下的传输效率为

(13)

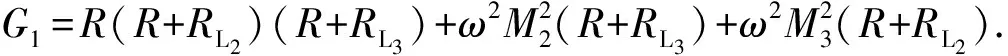
2.2 CMT分析

3个线圈的CMT分析和两个线圈的CMT分析方法类似，如下所示：

jK13a3(t)+Fs(t)

(14)

(15)

(16)

(17)

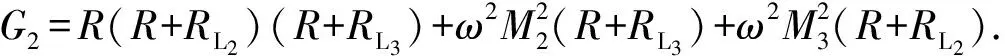
3 3个负载电路的传输效率分析

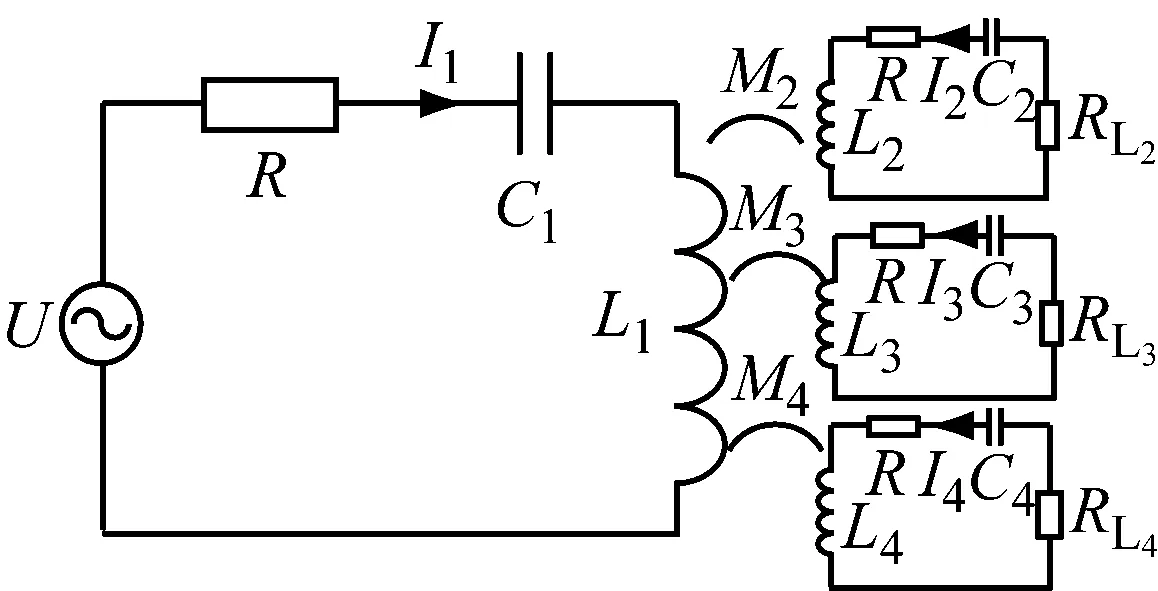
图3 3个负载线圈的CPT拓扑结构

对于图3中3个负载电路的拓扑结构，用同样的方法能够证明用集总参数分析方法和CMT求传输效率是相同的.

(18)

(19)

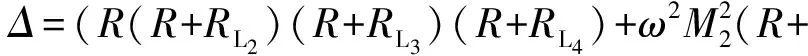
求得传输效率公式为

(20)

4 n-1个负载电路的传输效率分析

用集总参数分析图4拓扑结构，图4有n-1个负载线圈，有n个方程，分别为

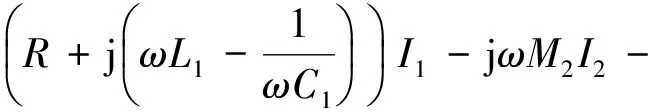
…-jωMnIn

(21)

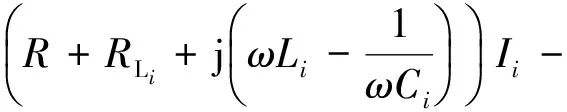
jωMiI1(i=2,…,n)

(22)

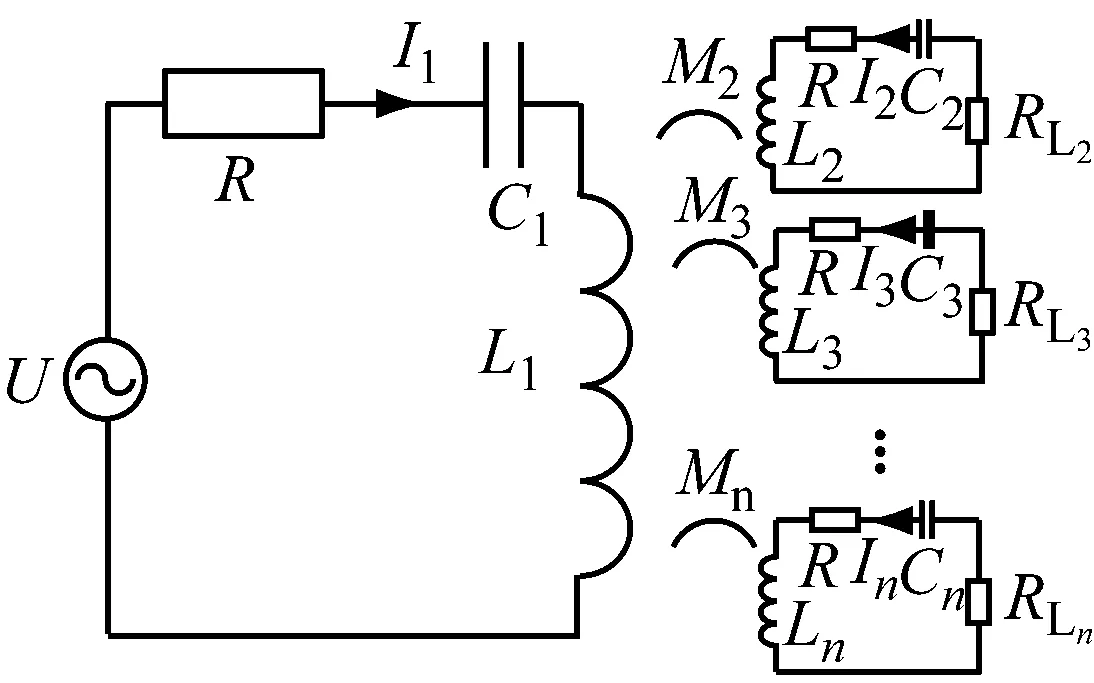
图4 n-1个负载线圈的CPT拓扑结构

解上述n个方程，并将I1，I2，…，In代入

(23)

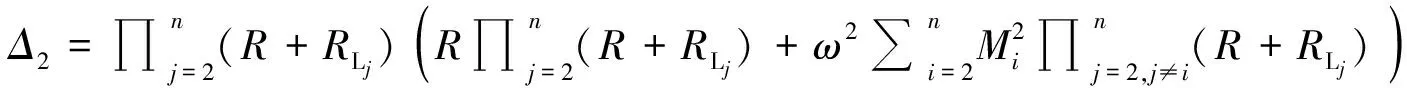
用CMT方法分析图4 的拓扑结构图，同样忽略励磁效应，由前面的方法可得

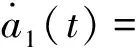
jK12a2(t)+…+jK1nan(t)+Fs(t)

(24)

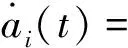
jK1ia1(t) (i=2,…,n)

(25)

将以上各变量代换，得到

(26)

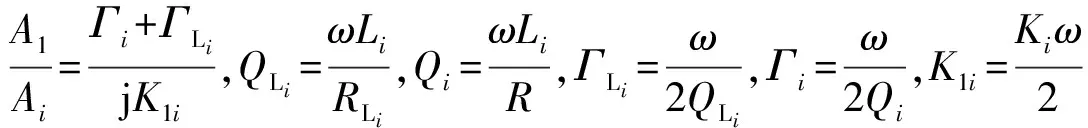
5 实验分析

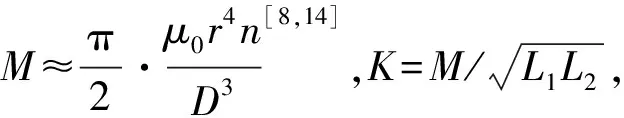
表1 实验参数

(a)单负载 (b)两个负载

图5传输效率曲线

由图中可以看出，由CMT和CT得到的效率值与测量值大致吻合.出现的小偏差可能是由于测量误差、系统的分布电容、分布电感以及线圈在移动过程中会出现不同轴现象引起的.值得注意的是，此方法仅适合于谐振状态.在谐振频率点，多负载CPT系统CMT下的效率计算公式与CT下的计算公式也完全等效.

物理学中常用的CMT用于同一平面的n个负载线圈的传输效率，从另一个角度阐述能量传递.接下来的工作就是进一步分析它的传输功率、系统品质因数和传输距离对系统的影响.

6 结束语

通过以上推导和实验可知，在谐振频率点上，用CMT的方法对谐振系统传输效率进行分析，结果与CT相同，CMT的提出让我们从另一个角度去分析CPT系统的效率问题，并考虑到CMT的计算阶次比CT的计算阶次降低一半，大大减少计算中的工作量，此方法可以推广到在同一平面的n个负载线圈的效率求解.

参考文献：

[1] KURS A, KARALIS A, MOFFATT R,etal. Wireless power transfer via strongly coupled magnetic resonances[J]. Sci, 2007, 317(5834): 83-86.

[2] 刘志军, 苏玉刚, 夏晨阳. 多负载感应耦合电能传输系统的传输效率研究[J]. 电子技术应用, 2011, 37(2): 64-70.

[3] 夏晨阳. 感应耦合电能传输系统能效特性的分析与优化研究[D]. 重庆: 重庆大学, 2010.

[4] 赵彪, 陈希有, 于庆广. 用于非接触电能传输的自适应谐振技术原理[J]. 电工电能新技术, 2010, 29(2): 33-37.

[5] 傅文珍, 张波, 丘东元, 等.自谐振线圈耦合式电能无线传输的最大效率分析与设计[J]. 中国电机工程学报, 2009, 29(18): 21-26.

[6] 杨民生, 王耀南, 欧阳红林. 新型无接触电能传输系统多负载解耦控制研究[J]. 湖南大学学报, 2007, 34(10): 53-56.

[7] 谢卫, 汪晓燕, 赵冰洁. 基于无功补偿的滑动变压器建模与仿真[J]. 上海海事大学学报, 2008, 29(2): 26-29.

[8] IMURA T, HORI Y. Maxing air gap and efficiency of magnetic resonant coupling for wireless power transfer using equivalent circuit and neumann formula[J]. IEEE Trans on Ind Electron, 2011, 58(10): 4746-4752.

[9] KARALIS A, JOANNOPOULOS J D, SOLJACIC M. Efficient wireless non-radiative mid-range energy transfer[J]. Ann Physics, 2008, 323(1): 34-48.

[10] 刘宿城, 周雒维. 近场磁谐振耦合能量传输系统的建模与分析[J]. 电源学报, 2011(1): 51-56.

[11] NIU Wangqiang, GU Wei, CHU Jianxin,etal. Coupled-mode analysis of frequency splitting phenomena in CPT systems[J]. Electronic Letter, 2012, 48(12): 723-724.

[12] 牛王强, 沈爱弟, 顾伟, 等. 可变负载非接触电能传输系统的无功功率补偿[J]. 上海海事大学学报, 2011, 32(1): 49-53.

[13] KIANI M, GHOVANOLOO M.The circuit theory behind coupled-mode magnetic resonance-based wireless power transmission[J]. IEEE Trans Circuits & Systems, 2012, 59(8): 1-10.

[14] 沈雄, 刘以建. 基于脉宽调制集成驱动的车载直流变换器[J]. 上海海事大学学报, 2005, 26(2): 60-63.