GPS-陀螺全站仪的研究

胡荣明，贺俊斌

（西安科技大学测绘科学与技术学院，陕西西安 710054）

一、引 言

陀螺全站仪是由陀螺仪和全站仪组合而成的，兼具陀螺仪和全站仪的特性及优势［1］。全站仪能够很好地实现数据的接收、显示、存储，并在全站仪上开发相应的通信与数据处理程序，提高了陀螺定向的数据处理能力与自动化程度［2］。

在陀螺定向工程中，最后需要求出的是陀螺定向边的坐标方位角。根据地面已知点数据获取已知边的坐标方位角，陀螺全站仪可测得数据为陀螺方位角，此时若能求得地面测站点在高斯平面的子午线收敛角，就可求出陀螺全站仪的仪器常数。而通常子午线收敛角的计算是根据设站点的大地坐标或平面坐标求得的。本文研究将GPS单点定位技术安置在陀螺全站仪上，实现设站点坐标的快速测定，并且拟通过设计内置解算软件实现陀螺定向内、外业一体化，直接输出定向边的坐标方位角。

二、GPS-陀螺全站仪组成及定向方法

1.GPS-陀螺全站仪组成

GPS-陀螺全站仪是将GPS接收机、陀螺仪、全站仪组合在一起形成的全新的仪器，同时能够将GPS接收机所测的数据信息反馈给陀螺仪，为陀螺仪的寻北提供数据支持。GPS-陀螺全站仪每个部件的作用各不相同，GPS接收机是用来测定测站点的大地坐标或平面坐标，陀螺全站仪则能够测量定向边的陀螺方位角。

2.GPS-陀螺全站仪定向方法

地下定向边陀螺方位角测量应采用“地面已知边（3）—地下定向边（2）—地面已知边（3）”的测量程序，陀螺仪定向原理如图1所示。

图1 陀螺仪定向示意图

（1）地面已知边上测定仪器常数及子午线收敛角

根据图1可知，CD边为地面已知边，地理方位角为A0，坐标方位角为α0。在C点安置GPS-陀螺经纬仪，独立观测3次，通过观测可得出CD边的陀螺方位角αT；根据GPS接收机观测数据，通过内置子午线收敛角计算程序求得测站点C的子午线收敛角γ0。可得仪器常数为

（2）井下定向边上测定陀螺方位角

在图1中，仪器安置在C'点上，独立观测两次，可测得C'D'边的陀螺方位角α'T。并将数据存储到计算机中，取陀螺方位角的平均值作为定向边的陀螺方位角。定向边的地理方位角为

（3）重新测定仪器常数

仪器在完成井下定向测量后，应该在地面已知边上重新测定仪器常数3次，然后求出仪器常数的平均值，并将数据存储到计算机中。

（4）求解井下定向边的坐标方位角

根据图1可知，仪器常数的计算公式为

井下定向边的坐标方位角为

将式（4）代入式（5）则可得出

根据式（6）可知，子午线收敛角、陀螺方位角是影响陀螺定向精度的主要因素。陀螺方位角对陀螺定向精度的影响主要是来自于陀螺定向观测过程中仪器的对中、整平，以及已知边位置的选择［3］。本文主要分析GPS接收机测定的坐标计算子午线收敛角能否达到陀螺定向的精度要求。

三、子午线收敛角的影响因素及大小

1.子午线收敛角的影响因素

子午线收敛角即指在高斯平面上任意一点的子午线方向与坐标纵轴之间的夹角，通常用γ表示［4］。平面子午线收敛角γ可由大地坐标（B，L）算得，也可由平面坐标（x，y）算得。下面分别列出它们的计算公式:

1）由大地坐标（B，L）计算平面子午线收敛角γ的公式为

2）由平面坐标（x，y）计算平面子午线收敛角γ的公式为

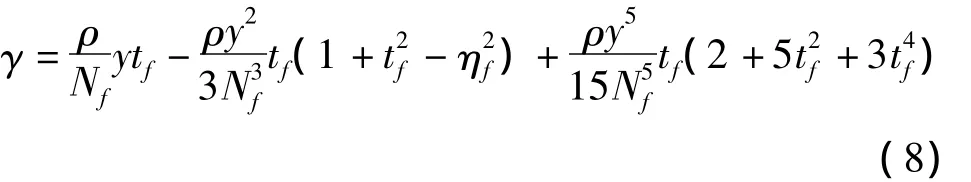
由式（7）、式（8）可知，子午线收敛角的特性有:①γ为l的奇函数，而且l越大，γ也就越大；②γ有正负，当点位于中央子午线以东时，γ为正；位于子午线以西时，γ为负；③ 当l不变时，则γ随纬度的增加而增大［5］。

2.纬度与经差对子午线收敛角精度的影响

根据式（7）可知，子午线收敛角的精度与测站点的大地坐标或高斯平面坐标有关。对于高精度陀螺定向（Gyromat2000型陀螺经纬仪实测精度为3″，Y/J＇TG-1陀螺全站仪一次定向中误差标称为7″）而言，子午线收敛角的测定精度必须控制在2″之内。根据式（7），探讨当经差l不变时，欲使子午线收敛角γ的变化范围在1″内，其随纬度的变化情况（见表1）。

表1 经差l不变时，纬度B的精度对子午线收敛角精度的影响 （″）

由表1可知，经差越大、纬度越小，子午线收敛角的变化区域越小，即受纬度变化的影响越大，但是纬度变化都在15″以上。

根据纬度对子午线收敛角的影响数据，代入式（9）可知，子午线收敛角在X轴（东西方向）上点位精度的要求，结果见表2。

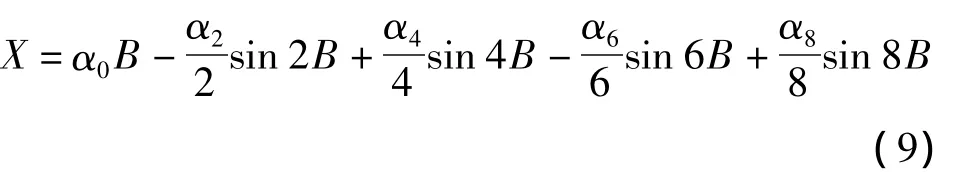
表2 子午线弧长随纬度的变化情况 m

其次，需要探讨的是经差l与子午线收敛角大小变化在2″之内时的变化规律。首先当纬度B不变时，要想使子午线收敛角变化在2″范围内，经差Δl的变化情况见表3。

将表（3）数据代入式（10）得出子午线收敛角在南北方向上的点位精度要求。

表3 纬度不变，经差精度对子午线收敛角的影响 （″）

根据数据表1～表4可知，即使在纬度为60°的高纬度地区，子午线收敛角变化在2″的范围内，其南北方向（即y轴）上点位的精度要求在30 m以内即可；由于纬度对子午线收敛角的影响因素较小，其东西方向（即x轴）上的点位精度要求只需满足在百米之内不会影响子午线收敛角的精度。而中纬度30°地区y轴的精度要求在50 m即可满足子午线收敛角的精度要求，不会影响陀螺定向的精度。

表4 平行圈弧长随经差变化情况 m

四、GPS单点定位技术及精度分析

根据目前科学技术的发展，利用GPS单点定位具有高精度、全天候、全球性等特点为陀螺定向中子午线收敛角的测定带来了便利。

1.单点定位技术

标准GPS单点定位技术（SPP）是利用码伪距观测量，通过接收4颗以上GPS卫星，由广播星历得到各历元的卫星位置和钟差，利用空间定位后方交会的原理，即可求得接收机的位置和钟差［6］。

现代GPS精密单点定位技术（PPP）广泛采用码伪距和载波相位观测量来提高定位精度［7］。随着IGS提供的精密星历和卫星钟差精度的不断提高，以及接收机性能的不断完善，大气改正模型和改正方法也在不断深入［8-10］。目前，武汉大学研制的PANDA软件实现了获取精确GPS卫星轨道、卫星钟差、误差改正模型，由于其软件本身可以定轨，进而实现了实时精密单点定位［11］。

2.坐标转换原理

由于GPS卫星星历是以WGS-84坐标系为基础建立的，因此GPS单点定位的坐标属于WGS-84坐标系。子午线收敛角是高斯平面上任意一点的子午线方向与坐标纵轴之间的夹角，故需将GPS测量成果转换成1954北京坐标系或1980西安坐标系下的坐标成果。采用空间转换模型，将WGS-84坐标转换成1954北京坐标。GPS-陀螺全站仪具备参数转换模块，输入该地区的转换参数，可实现不同坐标系之间的转换。

3.GPS单点定位技术精度分析

GPS接收机单点定位误差的大小取决于接收机处理器芯片的性能和载波星历，标准GPS单点定位技术是目前最常用的GPS定位技术，由于其具有高精度、全天候的技术有点，目前已广泛应用于测绘领域。GPS接收机目前静态定位精度可达2 m，动态定位精度在3 m之内［12］。便携式GPS接收机在定位时长在5 min之后，观测数据才能稳定，目前GPS定位精度可达10 m之内。

目前，武汉大学采用IGS提供的超快速预报星历可实现实时精密单点定位服务，在仪器初始化30 min之后，水平方向定位精度达到10 cm以下。

陀螺定向属于高精度测量，对子午线收敛角的精度要求比较高，而目前GPS单点定位技术都可保证GPS接收机所测数据在纬度在60°范围内达到精度要求（高纬度地区B为60°时，平面坐标精度小于20 m）。

五、GPS-陀螺全站仪功能模块及流程分析

GPS-陀螺全站仪采用内外业一体化的思想设计，将陀螺定向观测数据及已知点数据直接存储到全站仪计算机中，通过设计内置解算软件为定向测量提供已知边坐标方位角、地面测站点子午线收敛角、井下测站点子午线收敛角、地面已知边陀螺方位角、井下陀螺边方位角、仪器常数等数据。根据陀螺定向的原理及方法，本文对GPS-陀螺全站仪的功能模块进行了分析研究（如图2所示），通过内置的软件实现井下定向边的坐标方位角解算，省去了繁琐的内业计算过程，并对GPS-陀螺全站仪的数据处理流程进行总结（如图3所示），提高了陀螺定向作业效率，推动了技术向更高层次的发展。功能模块包括:

图2 GPS-陀螺全站仪数据处理流程图

图3 功能模块图

1）建立工程:创建工程的名称、时间，选择工程的坐标系（1954北京坐标系、1980西安坐标系、独立坐标系）。

2）数据录入:将地面已知点坐标和井下测站点坐标输入到GPS-陀螺全站仪中。

3）数据存储:将GPS、全站仪、陀螺仪数据存储到GPS-陀螺全站仪的计算机中，便于后续计算。

4）坐标方位角解算模块:利用地面已知点数据计算地面已知边的坐标方位角。

5）坐标转换模块:其一，是将GPS接收机所测得的WGS-84坐标转换为高斯平面坐标（1954北京坐标系或1980西安坐标系）；其二，若是独立坐标系，进行相对位置关系解算。

6）坐标正反算模块:对坐标转换后的数据进行处理，由于利用大地坐标计算子午线收敛角的算法比较合理，易于编写，故需坐标正反算。

7）子午线收敛角计算模块:根据处理好的测站点数据，解算测站点的子午线收敛角。

8）定向解算模块:将以上数据整合处理，通过陀螺定向解算公式，直接求得定向边的坐标方位角。

9）成果显示输出:将陀螺定向数据成果通过显示屏幕输出，输出的成果包括地面已知边坐标方位角、测站点子午线收敛角、井下测站点子午线收敛角、地面陀螺方位角、井下定向边陀螺方位角、井下定向边坐标方位角。

六、结 论

本文从理论方面对GPS-陀螺全站仪研究的可行性进行分析，得出以下几点结论:

1）对于高精度陀螺定向（Y/J＇TG-1陀螺全站仪一次定向中误差标称为7″）而言，子午线收敛角精度控制在2″之内，即使在高纬度地区（B=60°），测站点坐标可在的精度要求为x轴上坐标变化在百米之内，y轴不能超过30 m即可。在中纬度地区（30°～40°）y轴只需不超过40 m，平面坐标精度要求随着纬度和经差的减小而逐步降低。

2）不论是标准 GPS单点定位，还是GPS精密单点定位技术，其精度都可达到陀螺定向中子午线收敛角的精度要求。GPS定位技术可以应用于高精度陀螺定向。

3）GPS-陀螺全站仪的研究是将GPS接收机、陀螺仪、全站仪组合在一体的全新的陀螺定向仪器。将通信技术、数据存储技术、数据处理相结合，可实现陀螺定向内外业一体化。

［1］ 黎明，马军.子午线收敛角对陀螺定向精度影响的探讨［J］.测绘通报，2009（S0）:191-197.

［2］ 张海东，李宗春，范百兴，等.GeoBasic在陀螺全站仪联机通讯中的应用［J］.测绘科学，2005，30（5）:75-76.

［3］ 姜雁飞，胡荣明，杨联安.陀螺经纬仪在地里空间定向中的应用研究［J］.西北大学学报:自然科学版，2011，41（1）:145-149.

［4］ 张国良，朱家钰，顾和和.矿山测量学［M］.徐州:中国矿业大学出版社，2008:90-92.

［5］ 孔祥元，郭继明，刘宗泉，等.大地测量学基础［M］.武汉:武汉大学出版社，2005:178-179.

［6］ 李征航，黄劲松.GPS测量与数据处理［M］.武汉:武汉大学出版社，2005:110-111.

［7］ 陆晨曦，谭云华，朱柏承，等.单频精密单点定位中基于卡尔曼滤波的自适应导航算法［J］.北京大学学报:自然科学版，2011，47（4）:587-592.

［8］ ZUMBERGE J F，HEFLIN M B，JEFFERSON D C，et al.Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks［J］.Journal of Geophysical Research，1997，102（B3）:5005-5017.

［9］ HATCH R.Satellite Navigation Accuracy:Past，Present and Future［C］∥The 8th GNSS Workshop.Korea:［s.n.］，2001.

［10］ GAO Yang，CHEN Kongzhe.Performance Analysis of Precise Point Positioning Using Real-time Orbit and Clock Products［C］∥The 2004 International Symposium on GNSS/GPS.Sydney:［s.n.］，2004.

［11］ 耿涛，赵齐乐，刘经南，等.基于PANDA软件的实时精密单点定位研究［J］.武汉大学学报:信息科学版，2007，32（4）:312-315.

［12］ 刘伟平，郝金明，汪平.标准单点定位与精密单点定位精度对比研究［J］.测绘通报，2010（4）:5-7.