地震照明分析及其在地震采集设计中的应用

谢小碧，何永清，李培明

1 加州大学圣克鲁斯，美国加州 95064

2 东方地球物理公司采集技术支持部，河北涿州 072751

1 引 言

反射地震方法是获取地下结构的重要手段之一．其基本方法是由震源发出地震波传播到地下，遇到目标后反射回地表．携带着地下结构信息的反射波被设置在地表的接收系统记录到后，再经相应的数据处理方法对地下结构进行成像，从而得到关于地下结构的描述．在这一过程中，对地下结构的实际探测会受到诸多因素的制约．其中最主要的影响来自野外观测系统分布，复杂地质结构对波传播的影响，以及目标倾角等三项因素的作用．鉴于反射地震资料的现场采集和后期处理涉及非常高的成本，如果能在进行这些工作之前对观测系统的潜在探测能力提供一些评估，将大大降低现场采集成本．地震照明分析正是在给定观测系统和地下背景结构的情况下对反射地震探测能力提供定量描述的有效方法．地震照明分析可以有多方面的应用．例如，在进行实际数据采集前，可以事先针对工区的特点利用照明分析对不同的采集方案进行对比和优化，从而有可能在提高采集质量和效率的同时减少对昂贵采集设备和野外人工的投入．照明分析也可以作为分析成像质量的依据，确定某些成像现象究竟是地下结构的客观反映还是由于照明不均匀造成的假象．由于上覆介质的复杂性，出现照明不均匀引起的成像畸变或缺失是常见的现象．照明分析可以作为校正这些畸变的依据．经过校正后的地震成像有可能为后续的分析，例如速度分析、结构分析、地震属性提取、或岩石物理参数反演等，提供更为可靠的依据．

在早期工作中，照明分析常用比较粗糙的方法来进行．所用的模型通常基于均匀速度场、水平反射面和对称地震射线等假设．对照明的描述也仅限于覆盖次数等简单的参数．之后，随着射线方法的引入，地震照明分析方法得到了很大发展．射线方法可以提供波传播的方向和沿该方向的强度，从而使得在光滑非均匀介质中与角度有关的照明分析成为可能（例如，Bear等［1］；Muerdter和Ratcliff［2－3］；Muerdter等［4］），并进而应用于对成像分辨率和观测系统设计等与照明有关的研究（例如，Gelius等［5］；Lecomte等［6］；Hoffmann［7］）．但是，射线方法仍然是建立在高频渐进近似基础上的方法．它还不足以处理复杂模型中一系列的波动现象，例如散射、衍射和焦散等．因此，近年来，波动方程方法被引入到地震照明分析中，并取得了很好的结果．例如：Wu 和Chen［8］，Xie等［9－11］，Wu等［12］，Luo等［13］，孙伟家等［14］，张辉等［15］，Mao等［16］建立了利用单程波方程计算地震照明的方法．Xie和Yang［17］，Yang等［18］，裴正林［19］，Cao和Wu［20］将这一方法推广到全波方程，使其可以处理与逆时偏移（RTM）相对应的照明分析．Xie等［21］，Wu等［22］，Jin 等［23］和李万万［24］研究了地震照明与成像分辨率的关系以及利用照明对成像进行校正．Li和Dong［25］研究了照明分析在采集设计中的应用，Jin和Xu［26－27］，Menyoli等［28］，朱金平等［29］研究了对地下给定目标进行照明时对地表观测系统的要求．Jin 将其称为可视性分析（Visibility analysis）．Zheng等［30］将照明补偿应用到对上地幔的成像中．另外一些作者，Jin 和Walraven［31］；Jin等［23］；单联瑜等［32］；温书亮等［33］；赵虎等［34］讨论了照明分析在若干具体情况下的应用．在本文中，我们将阐明地震照明的一些基本概念，并讨论对不同照明描述的计算方法以及它们在地震采集设计中的可能应用．本文将注重于对物理概念的阐述而不追求公式的完备性．

2 照明分析的基本概念

用图1引入关于地震照明的若干重要概念．设想需要对地下的某个特定目标进行探测．用震源激发地震波并将其射入地下，经过传播到达成像目标．目标可以被看成是具有一定倾角的反射面．如果反射面能将地震波向上反射回地表，并到达接收器（如图1a所示），则我们能够得到相应的地震记录，并用它来构建反射面的像．如果由于某种原因，例如由于某种障碍使得地震波不能到达反射面，或者虽然地震波能够到达反射面但由于反射角的原因反射波不能回到接收器（如图1b所示），则不能获得来自特定目标的反射信号，因此也就不能对该目标进行成像．图1a所示的情况为目标可以被照明，图1b所示的情况为目标不能被照明．从图1中可以得到关于地震照明分析的如下一些重要概念．首先，地震照明不同于通常意义的照明．虽然照明分析是针对地下反射层进行的，但这一照明依赖于通过整个系统在地表得到反射能量的能力．它不但取决于震源的能量能否到达成像目标，而且取决于由目标反射的能量能否回到地面并被接收到，二者缺一不可．其次，图1表明了决定地震照明的三个关键因素，即（1）采集系统（包括震源和接收器的几何排列和所张孔径等）；（2）在下行和上行过程中上覆地层对地震波传播产生的影响，例如几何扩散，屏蔽或衰减等；（3）地震波在目标处的入射、散射方向以及目标的倾角，特别是三者之间的相对姿态．如图1所示，目标能否被照明或被照明的程度不但取决于目标所处的位置，而且取决于目标的倾角．所以，在目标附近研究反射面的倾角以及入射和散射角度是照明分析的关键．

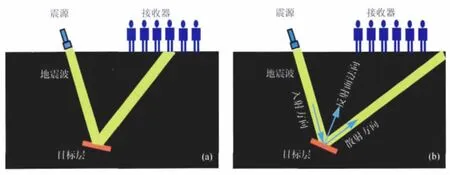
图1 地震照明的示意图（a）目标反射层可以被照明；（b）目标反射层不能被照明．Fig．1 Cartoon showing the concept of seismic illumination，with（a）a target that can be illuminated，and（b）a target that cannot be illuminated

近年来，随着地震波传播理论和计算机技术的快速发展，我们已能用各种模拟技术计算由地表激发，并经过复杂介质传播到地下的地震波．因此，可以将照明分析计算分为两步．第一步，根据实际采集系统的分布，计算从震源发出通过覆盖层到目标，以及从目标到接收器的地震波．这一步可以解决前面提到的影响照明的三项因素中的前两个，即采集系统孔径和上覆地层的影响．第二步，在目标附近将入射波和散射波都分解为沿不同方向传播的局部波束，并分析每一对入射－散射波束对于具有特定倾角的反射面的照明贡献．最后，将来自所有震源，所有接收器和所有角度对该目标的贡献叠加，从而得出整个采集系统对该目标的照明．其中第一步与常规地震波传播计算类似，可以看成是一种正演模拟．根据模型的复杂程度，对结果所需的精度以及所能承受的计算成本等，可以采用不同的计算方法，例如单程波方法或有限差分方法等．比较特殊的是第二步，即在目标附近对地震波做角度域分解并在角度域中计算入射和散射波对目标的照明贡献．这将是本文讨论的重点．下面，将分步骤讨论利用波动方程方法计算地震照明的相应方法．

3 地震波的角度域分解

如上所述，照明分析中的关键环节之一是确定波场中能量的传播方向．在这方面目前有下述一些方法可以利用．对于射线类的方法，因为射线是带有方向性的，所以可以直接利用射线在目标附近的指向来作为入射和散射的方向．而其能量可以通过动力学射线追踪以及通过计算单位面积中射线击中次数来得 到．Xu 等［35］和Brandsberg－Dahl等［36］对 此作了很大发展．当利用全波或单程波动方程来计算波场时，因为所得到的波动解中并不显含有波传播方向的信息．因此，从波场中提取传播方向并不是一个简单的问题．在这里有两类方法可用．第一种是局部波场分解方法，即在目标附近采集一小块波场，然后对这块波场进行局部慢度分析、小波分析、或加窗傅里叶分析，将波场信息转化为慢度域或波数域的信息，从而得到波传播的方向性信息．该方法既可以用于处理单程波波场也可以用于处理全波波场，同时也适用于含有P波和S波分量的弹性波场，并已经被用于研究地壳中导波能量分解［37－38］，地震照明分析［8－9，11－12，17－18，20，40－41］，地震成像分辨率和成 像校正研究［21－23］，以及成像道集提取［39，42－46］等目的．另一类方法是建立在计算波传播时波阵面的法方向上．例如计算波场的Poynting矢量［19，47］或计算P 波的位移极化矢量［48－49］并用它来表示波传播的方向．除此之外还有一类方法可以在成像过程中通过计算具有一定时空偏移距的像来提取波传播的方向［50－51］．不过这一方法需在成像过程中提取角度，而照明分析不涉及成像，因此不适用于照明计算．在本文中，我们着重介绍基于局部波场分解的角度域分解技术，并将结果用于照明分析．

如图2 所示，我们首先考虑由位于rs处的一个震源和位于rg处的一个接收器组成的简单观测系统对位于地下r处照明的贡献．原则上，由多个震源和接收器组成的任意复杂观测系统对目标的照明可以由上述简单观测系统的贡献叠加得到．从震源发出并到达目标处的波场可以用格林函数G（r；rs，ω）来表达，从目标散射后回到接收器的波场可以用另一个格林函数G（rg；r，ω）来表达．利用互易定理，这个波场也可以用从接收器到目标的波场G（r；rg，ω）来代替．这样可以简化计算．在实际应用中，可以根据具体目的和所需精度采用不同的波传播方法来计算这些格林函数，例如全波有限差分方法、单程波方法、几何射线或高斯射线方法等．原则上，照明可以用到达目标处波场的振幅来定义，也可以用到达目标处的能量流的强度来定义．基于能量流的照明定义与地震波成像的定义比较一致，也便于应用于研究成像分辨率或用于成像校正［11，21］．因此我们在这里用能量流强度来定义照明．到达目标的波场格林函数可以用下述公式分解为慢度域的波场：

图2 观测坐标系（蓝色）和目标坐标系（红色）Fig．2 Observation coordinate（blue）and the target coordinate（red）

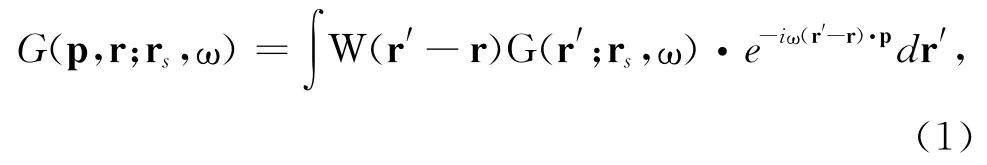
其中G（p，r；rs，ω）和G（p，r；rg，ω）分别是从震源和接收器到达目标的波场并且已经分解到慢度域，W（r′－r）是以目标位置r为中心的空间采样窗，p是慢度矢量，它指向波传播的方向，可以表达为p＝，其中p＝是采样窗中的平均速度，θ是指向波传播方向θ的单位矢量．因此，入射和散射格林函数可以表达为局部平面波（或波束）的叠加：

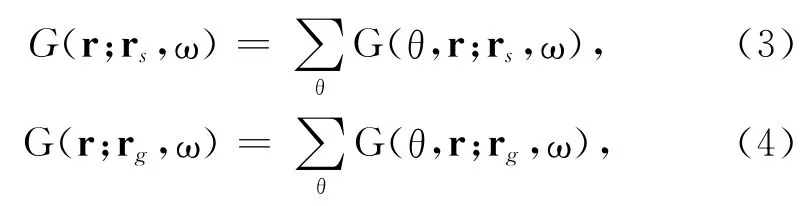
其中

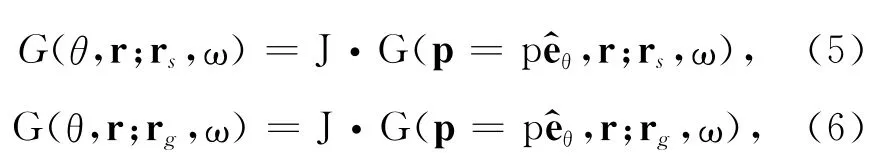
为角度域中的局部平面波（或波束），其中J为Jacobian因子，对二维波传播问题J＝ωp．

图3所示的是对地震波进行角度域分解的一个例子．图中部是速度模型，包括一个带有垂直速度梯度的背景介质和一个高速盐丘．叠加在速度上面的是一个由震源（五星）发出的波场快照．在波前的若干位置处（用圆点标明）进行了角度域分解．分解的结果见图的上部和下部的框中．由于频散关系，能量峰均落在不同半径的圆上．圆的半径是局部慢度．模型浅部速度低，因此圆的半径大．深部速度高，圆的半径小．峰的大小给出波的能量，峰在极坐标中的方位给出了波传播的方向．对比慢度域中得到的方向和波场快照中的波前传播方向，角度分解很好地提取了波传播的方向．特别是，当有多重路径存在的时候，即波由不同方向到达同一观测点的情况下（例如图中上排和下排的第2幅慢度图），这一方法可以同时确定多个来波方向．考虑到频散关系，二维空间的慢度分析只需要在一维的频散曲线（即图3的圆）上进行．三维空间的慢度分析只需要在二维的频散球面上进行（Yan和Xie［43］）．这样可以大大减少计算量．如果采用单程波方程来计算波场传播，则波场只能沿着向下方向传播．利用波的频散关系，对二维波传播问题可以用沿水平方向的一维变换来计算［39］．如果是三维波传播问题，则可以用水平面中的二维变换来计算［9，11］．除上述的慢度变换之外，也可以选择使用小波变换［8，12，20，16］或加窗傅里叶变换［45－46］．

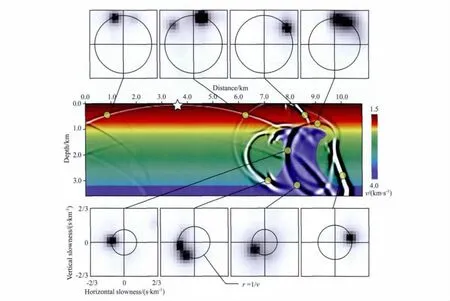
图3 地震波在角度域的分解图中部是包括一个高速盐丘的速度模型．叠加在上面的是一个由震源（五星）发出的波场快照．在波前的若干位置处（图中小圆圈标明的位置）进行了角度域分解．分解的结果画在图上部和下部的框中．能量峰在极坐标中的方位给出了波传播的方向．Fig．3 Angle domain decomposition of seismic wavesThe velocity model is composed of a high－velocity salt dome and a background with a vertical velocity gradient．Overlapped on the model are source（star）and the waveform snapshot．Angle decompositions are conducted at selected locations marked by circles．The decomposed wavefields are illustrated on the top and bottom where the locations of energy peaks in the polar coordinate indicate the wave propagation directions．

4 局部照明矩阵的建立

由（5）式和（6）式可以定义到达目标的入射和散射能流：

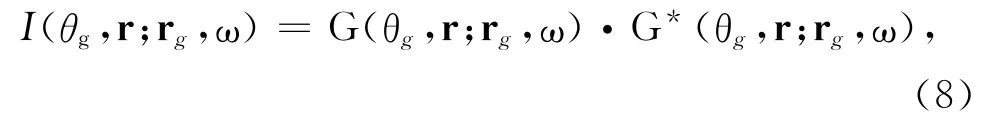
其中＊为取复共轭．每一对入射和散射方向分别为θs和θg的能流构成对r处目标照明的一部分贡献

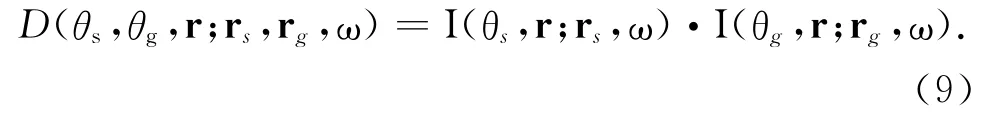
从一个采集系统到达目标的入射和散射波可以来自不同的方向．如果将θs和θg视为表示方向的脚标，则（9）式构成一个矩阵公式．矩阵D 的元素是所有可能的入射－散射对．注意（9）式是对一对震源－接收器（rs，rg）定义的．我们可以把它看成是照明的“格林函数”．一个由多个震源和接收器构成的复杂采集系统对照明的贡献可以通过对（9）式叠加得到

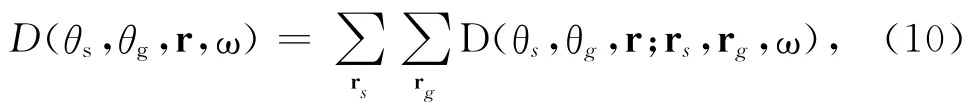
其中（rs，rg）的空间位置是根据采集系统的具体几何形状得到的．称（9）和（10）式中的D 为局部照明矩阵（local illumination matrix，或LIM）．“局部”是指这个矩阵是空间变量r的函数，空间各处的照明是不同的．照明矩阵中包括了所有可能的对目标的照明，所以可以通过研究D 来很方便地研究采集系统对r处目标的照明．

在上述方程中，θs和θg是相对于采集系统建立的坐标．利用坐标转换θd＝（θg＋θs）/2和θr＝（θgθs）/2，可以得到建立在目标坐标系下的照明矩阵D（θd，θr，r，ω），其中θd和θr分别是反射面的倾角和反射角（见图2）．建立在目标坐标系中的公式更适合于研究对于特定目标的照明．

为了更好地理解照明矩阵的结构以及它与采集系统坐标系和目标坐标系的关系，图4是关于照明矩阵结构的示意图．图上部和左侧分别列出了从入射波和散射波分解出来的具有不同方向的波束，范围为±90°，相当于单程波方法的传播角度范围．图中的矩阵给出了不同入射－散射波束所能产生的所有组合，即（9）式或（10）式．根据Snell定律，每对组合将对应于一个具有特定倾角的反射面．该反射面的法向量正好是入射－散射方向的角平分线．换句话说，每一对组合波恰巧可以对一个具有特定倾角的反射面提供照明．我们只要计算每一对组合波的强度就能获得采集系统对具有相应倾角反射面的照明．整个照明矩阵汇集了该处有关照明的全部信息，通过研究局部照明矩阵，可以导出适用于不同目的的照明描述．

图4 照明矩阵的结构示意图上部和左侧分别为从入射波和散射波分解出来的具有不同方向的波束．中部的矩阵列出了由不同入射－散射方向所能产生的所有照明组合．Fig．4 The structure of an illumination matrixListed on the top and left are incident and scattered waves which are decomposed into beams along different directions．In the center is the illumination matrix with its elements composed of illumination combinations from all possible incident－scattering directions．

局部照明矩阵具有一定的对称性．图4的矩阵中沿横方向对应于不同的入射角θs，因此每一竖列元素都具有相同的入射角．沿竖直方向对应于不同散射角θg，每一横行元素都对应于相同的散射角．因此，矩阵的纵横方向分别对应于采集系统坐标系中的θg和θs轴［39］．在矩阵主对角线（即从左上到右下）及与之平行的每一斜列上的元素都对应于一个相同的倾角θd．为便于看清，在每个斜列中对其中一个元素标明了相应的倾角．作为例子，图中用蓝色阴影标明了分别具有0°和－45°倾角的斜列．另一方面，在副对角线（即从右上到左下）和与之平行的斜列中，每列元素对应于一个相同的反射角θr（即入射波或散射波与反射面法方向所成的角）．例如，由黄色阴影标明的为所有具有30°反射角的元素．因此，矩阵的主对角线方向对应于目标坐标系中的反射角轴θr，而副对角线方向对应于倾角轴θd［39］．利用这些对称性可以很方便地对矩阵元素进行坐标变换．例如可以将（9）式或（10）式中的D（θs，θg，r，ω）变换成D（θd，θr，r，ω），以便于根据目标反射层的参数从照明矩阵中抽取与特定目的有关的元素构成所需的照明．在三维情况下对称性将更为复杂，但类似的关系仍然存在．

5 不同的照明描述方式及具体计算方法

5．1 模型中照明矩阵的计算

如上所述，照明矩阵是照明分析中最基本的，它包含了关于某点附近照明的全部信息，包括所有可能涉及到的来波方向和反射面倾角．各种不同类型的照明描述都可以从照明矩阵中提取．因此首先研究照明矩阵．在此利用全波有限差分来计算格林函数，并用（5）—（6）式将目标附近的入射和散射波分解为角度域的波束．然后利用（9）—（10）式计算出给定空间位置的照明矩阵．仍然从最简单的情况开始分析．图5给出了对单个震源和单个接收器的计算例子．图中由上到下每一行对应不同的模型和观测方式．注意，因为使用了全波格林函数，入射和散射角的范围均为±180°．首先研究图5a表示的最简单的情况，由地表处相互位置很接近的一对震源－接收器在均匀介质中产生的对地下－45°反射面的照明．从图中可以看到，在目标所在位置计算出的照明矩阵中由这一对震源－接收器产生的照明能量恰好落在倾角为－45°处．此外，由于震源和接收器之间的距离很近，入射波和散射波沿接近正交的方向抵达反射面，因此反射角（入射或散射方向相对于反射面法向的夹角）应该接近0°．相应的照明能量恰好落在反射角约为0°处．从图中我们也可以看到，在一个均匀模型中，一个地表采集系统只能探测到小于90°倾角的反射层．图5b和图5c中则表示了同样的采集系统在具有垂直梯度的速度模型中的照明情况．从中可以看到，在这种情况下，地表采集系统不仅可以探测到90°倾角的反射面，而且可以对大于90°的倒悬结构进行成像．对比它们的照明矩阵，照明能量落在倾角为90°和120°的位置，相应的反射角仍为0°左右，即照明是由接近正入射的能量提供的．在图5d中，采集系统换成了地表激发井下接收的VSP采集方式，速度模型为均匀模型．在这种采集方式下，可以得到对于垂直结构的像．在照明矩阵中相应的能量落在倾角90°处．因为震源与接收器拉开了一段距离，在目标处入射、反射方向有一个张角，所以矩阵中照明能量峰的反射角不为0．

图5 对单个震源和单个接收器产生的局部照明矩阵的计算例子（a）地表采集均匀速度模型45°反射面；（b）地表采集梯度速度模型90°反射面；（c）地表采集梯度速度模型120°反射面；（d）VSP采集均匀速度 模型90°反射面．图中由上到下每一行对应不同的模型和采集方式．左边是相应的局部照明矩阵．右边一列画出了震源（五角星），接收器（小方形），反射面的位置和倾角（短黄线），以及大致的射线路径（黑虚线）．叠加在模型空间的色彩为相应于该角度的采集倾角响应．Fig．5 Examples of local illumination matrixes from single source－receiver pairs．From top to bottom are for different models and acquisitions．Shown in the left column are illumination matrixes and in the right column are acquisition dip responses．The sources（stars），receivers（squares），reflectors（yellow bars）and approximate ray paths（dashed lines）are also marked in the figure．

图6中所示的是在一个盐丘模型中得到的由整个采集系统产生的照明矩阵．速度模型与图3中所用的相同，其中包含一个具有垂直速度梯度的背景介质和一个具有陡峭侧翼和悬挂结构的盐丘．采集系统的震源覆盖整个地表，每一个震源带有一个左侧单向接收器排列，长3．6km．作为示意，图5的速度模型上画出了一个震源和与它相应的接收器排列．我们计算了模型中不同部位处（由白色十字标明）的局部照明矩阵．在这些矩阵中，照明范围主要集中在其右下部的三角形区域中，这主要是由于单边接收器排列造成的．由于速度梯度和分界面的存在，介质中存在回折波和反射波．对于大多数部位来说，照明的入射角和散射角均大于±90°的范围，因此可以提供对于直立界面的照明．注意照明矩阵中的虚线框圈定的是入射角和散射角限于±90°的范围．它们是单程波方法所能达到的区域．对于整个照明矩阵，入射角和散射角可达到±180°，这是全波方法所能计算的范围．显然，全波方法可以覆盖更大的照明计算范围．这一点对于研究与逆时偏移有关的照明问题尤为重要．在接近盐体的地方，由于波通过高速盐体产生的反射和折射，局部照明矩阵的形态变得比较复杂．局部照明矩阵为研究复杂情况下的地震照明提供了一个比较好的分析工具．

图6 在一个具有速度梯度和盐丘的模型中不同部位处由整个采集系统得到的局部照明矩阵（速度模型同图3）Fig．6 Local illumination matrixes at selected locations generated by the entire acquisition system（The velocity model is the same as used in Fig．3）

5．2 采集系统对目标的角度覆盖以及照明强度随反射角的分布

虽然成像本身往往只依赖于照明的总强度，但还是有很多分析依赖于照明对反射角的覆盖范围．例如，进行偏移速度分析时常常需要产生成像角道集（Angle domain common image gather）；研究潜在油储特性时往往要依赖于振幅角道集（AVA 或AVO），等等．这些都依赖于地震波照射到目标时的反射角分布．事实上，在照明矩阵中已经包含了关于它们的信息．我们可以把照明矩阵结构图（图4）当作“结构量板”覆盖在计算出的照明矩阵上进行分析．例如，在图7a中所示的是图5a中计算出的照明矩阵，上覆了结构量板．其中对应于－45°倾角的斜列已用黑虚线框标明．前边提到过，在照明矩阵中沿主对角线方向是反射角轴．因此，把这个框中的照明能量抽取出来就是在该点对一个具有－45°倾角的反射面上照明能量随反射角的分布．在上述具体例子中，矩阵中具有显著能量的部分集中在反射角为0°附近，其它反射角处基本上没有照明．因此，一个如图5a所示的由一个震源和一个接收器组成的采集系统对于一个－45°目标能够进行照明，但照明角是很窄的．图7b中所示的照明矩阵由多个地表震源产生，类似于图6左上角处的情况．如果目标是一个0°倾角的水平反射面，则与它对应的照明相应于图7b中的黑虚线框．矩阵中被照明的部位具有比较大的反射角范围．综上，由（9）式计算出目标r处的照明矩阵后，先从采集系统坐标系（θs，θg）变换到目标坐标系（θd，θr），然后用“结构量板”按照r处反射面的倾角θd（r）提取出相应的照明就可以得到照明随反射角的分布．即

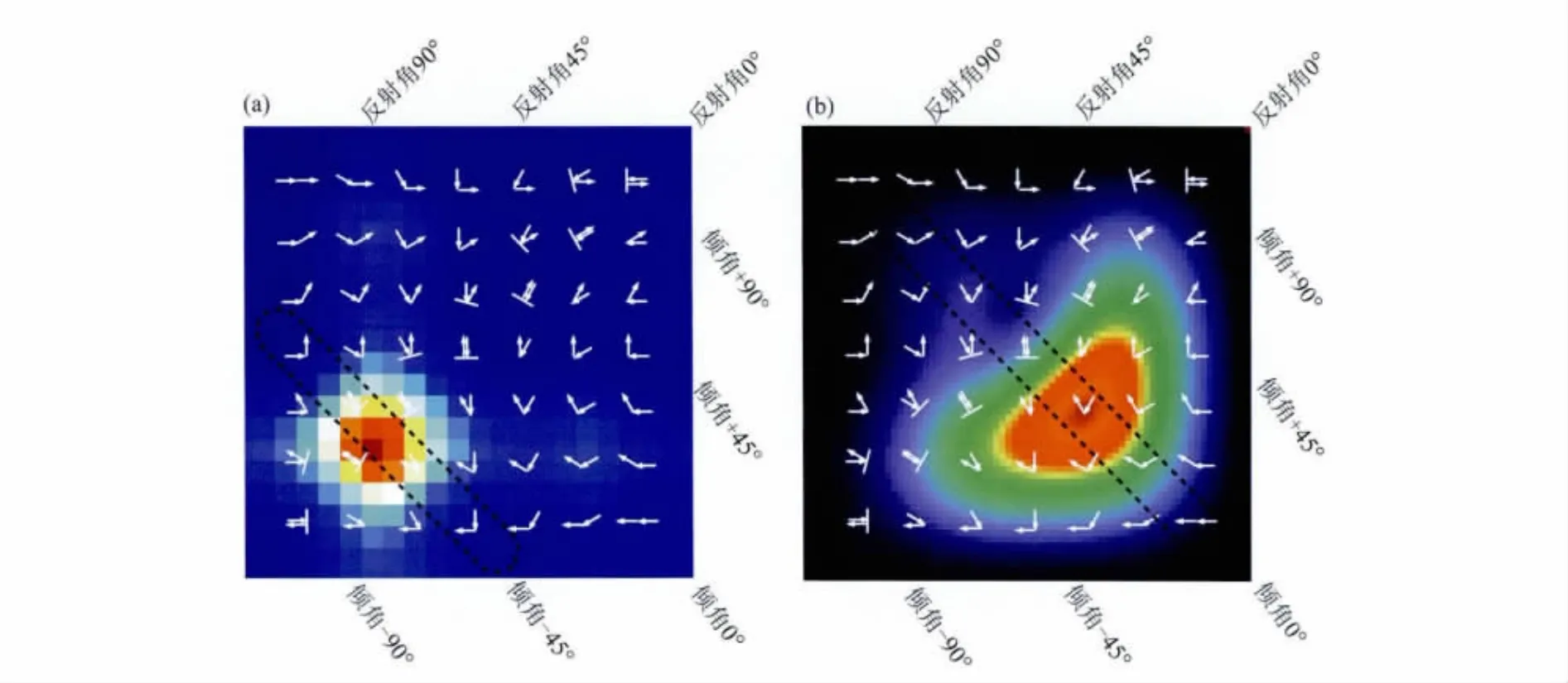
图7 照明矩阵结构图覆盖在计算出的照明矩阵上（a）由单一震源和单一接收器产生的对－45°倾角界面的情况；（b）由多个震源和接收器产生的对水平反射面的情况．Fig．7 Energy distributions in local illumination matrixesTo help understand，the structure of the LIM（Fig．4）is overlapped on the energy distributions．（a）The LIM from a single source－receiver pair and for a－45°dipping angle；（b）The LIM from a multi－source acquisition system and for a horizontal reflector．

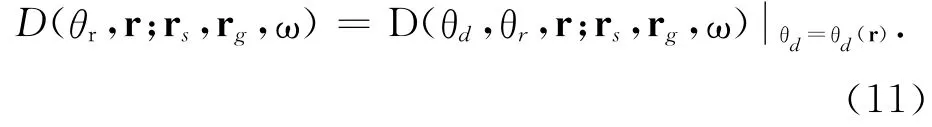
或对于整个采集系统的照明矩阵（10）式有

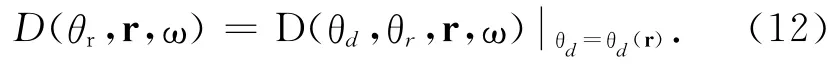
图8中即为一个照明随反射角分布的例子．其中图8a所示的是一个均匀速度模型，其中含有两个待探测的反射面．震源均匀地分布在地表．其观测系统为长3km 的单边接收排列．作为示意，图中画出了一个震源以及相应的接收器．在反射面的若干部位画出了照明能量随反射角分布的扇形图．由于利用了震源与接收器的可互易性，反射角表现为双边的．从图中可以看到，通常在浅部的照明角比较宽，越往深处照明角越窄．在较平坦的部位照明角比较宽．在比较陡峭的部位，照明角很窄且振幅比较小．图8b给出沿整个反射面的照明角度分布，其中横坐标是水平距离，纵坐标是反射角．可以看到，在若干陡倾角处照明的反射角很小．例如，在反射面1上，产生照明角度覆盖极小值处正好对应于三段具有陡倾角的部位．因此，提取角道集或进行AVA 分析应选择具有较宽照明角度分布的部位，不宜在照明覆盖角度很小的部位进行．

5．3 对特定目标的照明计算（target oriented illumination）

如果对模型中反射面的空间位置和倾角有一定的了解或估计，就可以针对这些反射面计算对它们的照明．具体方法是：首先根据反射面的位置沿着反射面计算照明矩阵，并确定反射面上每一点的倾角方向，即反射面的局部法向量（如图8a中扇形下面的短线所示）．然后根据倾角方向从照明矩阵中抽出相应于给定倾角方向的能量，这一步与前边提到的计算对目标的角度覆盖类似．最后，把从属于该倾角的具有不同反射角的能量叠加起来就得到对特定反射面的总照明．用公式表达即为

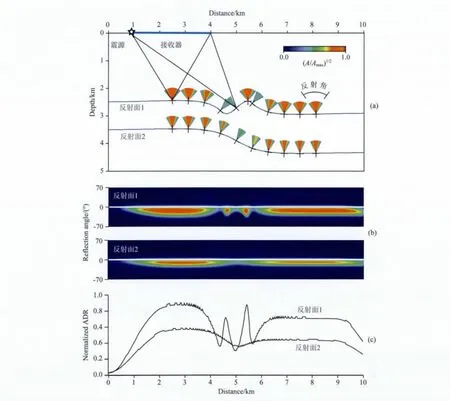
图8 采集系统对特定目标的照明（a）接收系统和反射面几何形态；（b）在反射面上照明能量随反射角的分布；（c）沿反射面的总照明强度．Fig．8 Target oriented illumination generated by the acquisition system（a）The geometry of the acquisition system and reflectors；（b）Illumination as a function of reflection angle along the target；（c）Acquisition dip response along the target．

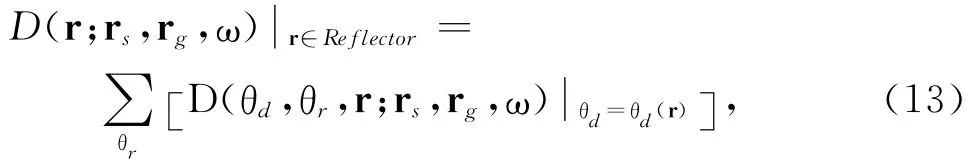
其中r∈Reflector表示照明计算在反射面处进行．对于表示整个采集系统的（10）式则有

图8c是在各个反射面上将具有不同照明角度的能量叠加得到的总照明．在图中可以看到，较平坦的部位具有较宽的角度覆盖范围，同时也有比较强的总照明．在比较陡峭的部位，角度覆盖范围窄，照明强度也比较弱．考虑到复杂情况下采集系统对反射面照明的不均匀性，所成的像常常不能反映界面的真实物理状况，例如像并不总与界面的反射系数成比例．分析对特定目标的照明有助于我们认识这一局限性或者对其进行校正［21－23］．

5．4 采集倾角响应及其计算

为计算采集系统对模型空间中任意位置处具有特定倾角的反射体的总照明，可以计算该点的照明矩阵，然后将该矩阵中相应于特定倾角的照明能量叠加就可以得到采集倾角响应（acquisition dip response或ADR）．在图7中这相当于把黑虚线框中相应于给定倾角的所有照明能量相加．如果将这种计算遍布空间所有的点，就可以得到整个模型中对给定倾角反射面的探测能力．值得指出的是，计算采集倾角响应与前边针对特定目标计算照明具有相似性．所不同的是，在这里并不需要模型中真的存在这些结构．它是本着“假定模型中处处存在具有这种倾角的反射面，对它们的探测能力将如何？”所进行的模拟．以图5a的情况为例，为计算全空间中的－45°采集倾角响应，先计算空间每一点处的局部照明矩阵．然后在每一点处将矩阵中相应于－45°倾角的能量加起来，就可以得到对该点一个假想－45°目标的倾角响应．如果相应于该倾角的元素能量几乎为0，则观测系统在该点附近对具有－45°目标的探测能力很弱．在图5a右侧模型空间中的色彩即为得到的倾角响应，其中红色代表高照明区，蓝色代表低照明区．图中的高照明区域与直观认识到的对－45°目标的照明区域是一致的．图5（b—d）的右侧显示了对其它几种情况计算出来的采集倾角响应的空间分布．

5．5 对地下反射体的可视性（Visibility）分析

对于给定的地表观测系统，通过照明分析可以得到对地下不同部位的照明．反过来，对于地下反射体的某些部位，也可以分析地表采集系统中哪些震源和接收器对该部位成像贡献最大．Jin和Xu［26－27］称其为“可视性分析”．研究（13）式可知，D（r；rs，rg，ω）给出的是一对震源－接收器对地下r处反射面的照明．通常给定采集系统（rs，rg）和反射面倾角θd（r），计算出D 并表达为模型空间中的照明D（r）．事实上，也可以将计算结果D 表达在采集系统空间（rs，rg）中，即为对r∈Reflector的“可视性”D（rs，rg）．它的含义是在r处具有倾角θd（r）的一段反射面能被位于（rs，rg）的一对震源－接收器探测到的能力．图9中所示的是可视性计算的例子．其中所用的模型与图8中所用的相同．在图9a中第1个反射面上用小方框标明了3段反射面I、II和III用于计算其可视性．计算中使用了361个震源，每个震源配有3km长的单边接收器排列（如图9a中所示），测线总长10km．计算结果显示在图9b中．其中纵坐标为震源的位置rs，横坐标是偏移距rg－rs．三幅小图分别对应于图9a中的三段反射体I、II和III，它们在测线中的位置也标在各幅小图中．图中色标表示经统一归一的可视性．从可视性图中可以看到，位于I处的反射面呈水平状，具有较好的可视性．震源在1km处即可探测到目标，但主要依赖于远端（faroffset）接收器．随着震源向右移动，更多的接收器对探测有贡献．由于是单边接收器矩阵，当震源移过目标后对该水平目标就没有了探测能力．由于具有比较大的倾角，对位于II处的可视性主要来自较远的震源，因此探测能力比较弱．位于III处的那段反射面处于一个峰顶，具有比较大的曲率．由于散射和衍射的作用，照明的角度覆盖范围很大，因此在很大一段范围中的震源和接收器都可以对它的可视性有贡献．虽然可视性的强度不是很高，但其综合效果使得对于峰顶部的探测能力很强．以上这些与照明分析及实际成像结果是对应的（参见图8b、c）．对于更加复杂的模型，例如对于盐丘下某些结构的可视性，将会更加复杂．可视性分析的优越性是可以根据重点目标部位找到在地表什么地方布设震源和接收器才能得到最佳成像结果，十分有利于采集设计．

图9 对反射体的可视性分析（a）反射体的位置，其中3个小方框标明的那些段落是进行可视性计算的部分；（b）可视性在震源－接收器空间的分布．Fig．9 The visibility analysis for a target（a）The geometry of the reflector，where the 3small squares indicate the locations the visibilities are calculated；（b）The visibility distributions in the sours－offset space．

6 照明分析在采集设计中的应用

如前所述，地震采集工作是一项成本巨大的工作．随着计算机功能的大幅提升，地震照明分析在地震采集设计中的应用越来越多［7，25，34］．以前，只能通过正演模拟的方法定性分析地下的照明情况，这是不完全的．本文所述的计算方法有助于对地下地质体的照明情况进行定量或半定量的分析．从而可以在下述方面有针对性地采取相应措施改善弱照明区的照明情况．

6．1 为采集系统总体布局设计提供参考

在对一待勘探区域规划采集方案时，需要决定诸如测线分布，测线移动或船行方向，线间距离等参数．根据勘探目的，地质构造以及目标层的特征等，可以用照明分析方法对候选采集方案进行验证，从中找到比较理想的方案．

6．2 采集阴影区的照明分析与补偿方法

地震照明分析可以得到目标区的照明能流变化，并可以使用不同的照明描述方式，例如体照明、目标定向照明等，定量化地表现．由此可以直观地看到采集阴影区的照明分布．也可以通过对目标的可视性分析，得出地表观测系统中哪些震源和接收器直接贡献于目标的阴影区．因此，在采集设计中就可以通过调整观测系统或加强部分区域的激发接收来改善阴影区的照明情况，并以此改善阴影区的成像品质．

6．3 分析和改善采集反射角与方位角的覆盖

如前所述，地震资料处理中不但要保证有足够的反射能量可以用于成像．对资料的进一步处理常常需要数据能够具有较好的角度覆盖．这一点对于速度分析、AVO 分析等常常起到决定性作用．通过局部波场的角度域分解，可以得到目标区反射角和方位角的分布．在对复杂地质体实施勘探前，可以先对不同采集系统布局方案进行试算，并对重要目标处的角度覆盖状况进行分析．如果分析结果认为这些部位的角度覆盖范围不能满足要求，则可以通过改变观测系统的布局，进行局部补充观测，甚至采用WAZ（wide azimuth）观测等来改善对目的层照明的方位角分布．

上述这些照明分析工作可以在计算机上反复进行，直到获得最佳方案．虽然室内计算并不能完全代替野外实验过程，但可以大大减少野外采集工作的风险，提高工作效率，节约勘探成本．

7 讨论和结论

本文阐述了关于地震照明分析的一系列基本概念．对地下结构的照明不仅取决于地震能量能否到达需要探测的目标，而且取决于从目标反射回来的能量是否能够回到地表并被接收到．在这里，地震波在目标处的入射方向，散射方向以及它们与反射面法线方向所成的角度起到重要的作用，因此是照明分析的关键．计算地震照明可大致分为下述几个步骤：

（1）计算由震源和接收器到达目标处的波场．

（2）在目标处将入射和散射波场分解为沿不同方向传播的波束．

（3）利用沿不同方向传播的入射和散射波束构建局部照明矩阵．

（4）按照不同的目的从照明矩阵中选择相应的元素组合成所需的照明．

我们分析了基于波动方程方法来计算若干种常用地震照明的具体方法．其中最主要的部分包括对波场的传播方向分解和局部照明矩阵的建立．照明矩阵包含关于目标照明的所有信息，其它各种关于照明的描述可以很方便地从照明矩阵中导出．给出了若干数值计算的实例，例如对特定反射面的照明，对全空间的采集倾角响应，对目标的照明角度覆盖，以及对目标可视性的计算等．为简单直观起见，所选例子大多是二维的，主要目的是阐明所述的计算方法．不过，文中所述的方法可以很容易地推广到三维问题．地震照明具有比较广泛的应用．在数据采集阶段，可以利用照明分析来帮助设计和优化采集系统，从而能够在付出较小的情况下得到较高质量的数据．在地震数据处理阶段，照明分析的结果可以帮助我们QC成像结果，识别成像过程中可能产生的干扰、假象、阴影区和畸变等．在获得地下结构的像后，可以利用照明资料来提升成像分辨率，矫正角度域的振幅，使得从地震成像中提取出的信息，例如RMO、AVO 等更加精确．从而使得后续的油储分析、岩性分析等建立在更加可靠的基础上．

（References）

［1］ Bear G，Liu C P，Lu R，et al．The construction of subsurface illumination and amplitude maps via ray tracing．The LeadingEdge，2000，19（7）：726－728．

［2］ Muerdter D，Ratcliff D．Understanding subsalt illumination through ray－trace modeling，Part 1：Simple 2－D salt models．TheLeadingEdge，2001，20（6）：578－594．

［3］ Muerdter D，Ratcliff D．Understanding subsalt illumination through ray－trace modeling，Part 3：Salt ridges and furrows，and the impact of acquisition orientation．TheLeadingEdge，2001，20（8）：803－816．

［4］ Muerdter D，Kelly M，Ratcliff D．Understanding subsalt illumination through ray－trace modeling，Part 2：Dipping salt bodies，salt peaks，and nonreciprocity of subsalt amplitude response．TheLeadingEdge，2001，20（7）：688－697．

［5］ Gelius L J，Lecomte I，Tabti H．Analysis of the resolution function in seismic prestack depth imaging．Geophysical Prospecting，2002，50（5）：505－515．

［6］ Lecomte I，Gjøystdal H，Drottning Å．Simulated prestack local imaging：a robust and efficient interpretation tool to control illumination，resolution，and time－lapse properties of reservoirs． 73rd Annual International Meeting， SEG，Expanded Abstracts，2003，1525－1528．

［7］ Hoffmann J．Illumination，resolution，and image quality of PP－and PS－waves for survey planning．TheLeadingEdge，2001，20（9）：1008－1014．

［8］ Wu R S，Chen L．Mapping directional illumination and acquisition－aperture efficacy by beamlet propagators．72nd Annual International Meeting，SEG，Expanded Abstracts，2002，1352－1355．

［9］ Xie X B，Jin S，Wu R S．Three－dimensional illumination analysis using wave equation based propagator．73rd Annual International Meeting，SEG，Expanded Abstracts，2003，989－992．

［10］ Xie X B，Jin S，Wu R S．Wave equation based illumination analysis．74th Annual International Meeting，SEG，Expanded Abstracts，2004，933－936．

［11］ Xie X B，Jin S W，Wu R S．Wave－equation－based seismic illumination analysis．Geophysics，2006，71（5）：S169－S177．

［12］ Wu R S，Chen L，Xie X B．Directional illumination and acquisition dip－response．65th Conference and Technical Exhibition，EAGE，Expanded abstracts，2003，P147．

［13］ Luo M Q，Cao J，Xie X B，et al．Comparison of illumination analyses using one－way and full－wave propagators．74th Annual International Meeting，SEG，Expanded Abstracts，2004，67－70．

［14］ 孙伟家，符力耘，碗学检．基于相位编码的地震照明度分析．石油地球物理勘探，2007，42（5）：539－543．

Sun W J，Fu L G，Wan X J．Phase encoding－based seismic illumination analysis．OilGeophysicalProspecting（in Chinese），2007，42（5）：539－543．

［15］ 张辉，王成祥，张剑锋．基于单程波方程的角度域照明分析．地球物理学报，2009，52（6）：1606－1614．

Zhang H，Wang C X，Zhang J F．One－way wave equation based illumination analysis in angle domain．ChineseJ．Geophys．（in Chinese），2009，52（6）：1606－1614．

［16］ Mao J，Wu R S，Gao J H．Directional illumination analysis using the local exponential frame．Geophysics，2010，75（4）：S163－S174．

［17］ Xie X B，Yang H．A full－wave equation based seismic illumination analysis method．70th Conference ＆ Technical Exhibition，EAGE，Expanded Abstracts，2008，P284．

［18］ Yang H，Xie X B，Luo M Q，et al．Target oriented full－wave equation based illumination analysis．78th Annual International Meeting，SEG，Expanded Abstracts，2008，2216－2220．

［19］ 裴正林．波动方程地震定向照明分析．石油地球物理勘探，2008，43（6）：645－651．

Pei Z L．Analysis on wave equation seismic directional illumination．OilGeophysicalProspecting（in Chinese），2008，43（6）：645－651．

［20］ Cao J，Wu R S．Full－wave directional illumination analysis in the frequency domain．Geophysics，2009，74（4）：S85－S93．

［21］ Xie X B，Wu R S，Fehler M，et al．Seismic resolution and illumination：A wave－equation－based analysis．75th Annual International Meeting，SEG，Expanded Abstracts，2005，1862－1865．

［22］ Wu R S，Xie X B，Fehler M，et al．Resolution analysis of seismic imaging．68th Conference ＆ Technical Exhibition，EAGE，Expanded Abstracts，2006，GO48．

［23］ Jin S W，Luo M Q，Xu S Y，et al，et al．Illumination amplitude correction with beamlet migration．TheLeading Edge，2006，25（9）：1046－1050．

［24］ 李万万．基于波动方程正演的地震观测系统设计．石油地球物理勘探，2008，43（2）：134－141．

Li W W．Design of seismic geometry based on wave equation forward simulation．OilGeophysicalProspecting（in Chinese），2008，43（2）：134－141．

［25］ Li P M，Dong L G．Optimal seismic survey design based on seismic wave illumination．68th Conference ＆ Technical Exhibition，EAGE，Expanded Abstracts，2006，F029．

［26］ Jin S，Xu S．Seismic visibility analysis and its applications to data acquisition and prestack migration．71st EAGE Annual Conference，Extended Abstract，2009，S015．

［27］ Jin S W，Xu S Y．Visibility analysis for target－oriented reverse time migration and optimizing acquisition parameters．TheLeadingEdge，2010，29：1373－1377．

［28］ Menyoli E，Jin S W，Xu S Y，et al．Visibility analysis for optimal imaging of target areas and its application to a Gulf of Mexico deep－water data set．Geophysics，2011，76（5）：WB119－WB126．

［29］ 朱金平，董良国，程玖兵．基于地震照明、面向勘探目标的三维观测系统优化设计．石油地球物理勘探，2011，46（3）：339－348．

Zhu J P，Dong L G，Cheng J B．Target－oriented 3Dseismic optimal geometry design based on seismic illumination．Oil GeophysicalProspecting（in Chinese），2011，46（3）：339－348．

［30］ Zheng Y C，Lay T，Flanagan M P，et al．Pervasive seismic wave reflectivity and metasomatism of the Tonga mantle wedge．Science，2007，316（5826）：855－859．

［31］ Jin S W，Walraven D．Wave equation GSP prestack depth migration and illumination．TheLeadingEdge，2003，22（7）：606－610．

［32］ 单联瑜，刘洪，匡斌等．基于胜利典型地质模型的波动方程地震波照明分析研究．石油地球物理勘探，2009，44（1）：1－6．

Shan L Y，Liu H，Kuang B，et al．Analysis on seismic wave illumination of wave equation based on Shengli typical geologic model．OilGeophysicalProspecting（in Chinese），44（1）：1－6．

［33］ 温书亮，尹成，李绪宣等．地震照明分析技术在深海地震数据采集设计中的应用．石油地球物理勘探，2011，46（4）：506－512．

Wen S L，Yin C，Li X X，et al．Seismic illumination method and its application in seismic geometry design in deep waters．OilGeophysicalProspecting（in Chinese），2011，46（4）：506－512．

［34］ 赵虎，尹成，李瑞等．基于目的层照明能量的炮点设计方法．石油物探，2011，49（5）：478－481．

Zhao H，Yin C，Li R，et al．Shot point design based on the illumination energy of target interval．GeophysicalProspecting forPetroleum（in Chinese），2011，49（5）：478－481．

［35］ Xu S，Chauris H，Lambaré G，et al．Common－angle migration：A strategy for imaging complex media．Geophysics，2001，66（6）：1877－1894．

［36］ Brandsberg－Dahl S，Ursin B，de Hoop M V．Seismic velocity analysis in the scattering－angle/azimuth domain．GeophysicalProspecting，2003，51（4）：295－314．

［37］ Xie X B，Lay T．The excitation of explosion Lg，a finitedifference investigation．Bull．Seis．Soc．Am．，1994，84：324－342．

［38］ Xie X B，Ge Z X，Lay T．Investigating explosion source energy partitioning and Lg－wave excitation using a finitedifference plus slowness analysis method．Bull．Seism．Soc．Am．，2005，95（6）：2412－2427．

［39］ Xie X B，Wu R S．Extracting angle domain information from migrated wavefield．72nd Annual International Meeting，SEG，Expanded Abstracts，2002，1360－1363．

［40］ Wu R S，Chen L．Mapping directional illumination and acquisition dip－response using beamlet propagators．Geophysics，2006，71：S147－S159．

［41］ Chen L， Wu R S，Chen Y． Target－oriented beamlet migration based on Gabor－Daubechies frame decomposition．Geophysics，2006，71（2）：S37－S52．

［42］ Yan R，Xie X B．A new angle－domain imaging condition for prestack reverse－time migration．79th Annual International Meeting，SEG，Expanded Abstracts，2009，2784－2788．

［43］ Yan R，Xie X B．A new angle－domain imaging condition for elastic reverse time migration．80th Annual International Meeting，SEG，Expanded Abstracts，2010，3181－3186．

［44］ Yan R，Xie X B．An angle－domain imaging condition for elastic reverse time migration and its application to angle gather extraction．Geophysics，2012，77（5）：S105－S115．

［45］ Zhang Y，Xu S，Tang B，et al．Angle gathers from reverse time migration．TheLeadingEdge，2010，29（11）：1364－1371．

［46］ Xu S，Zhang Y，Tang B．3Dangle gathers from reverse time migration．Geophysics，2011，76：S77－S92．

［47］ Yoon K，Marfurt K，Starr E W．Challenges in reverse－time migration．74th Annual International Meeting，SEG，Expanded Abstracts，2004，1057－1060．

［48］ Zhang Q S，McMechan G A．Direct vector－field method to obtain angle－domain common－image gathers from isotropic acoustic and elastic reverse time migration．Geophysics，2011a，76（5）：WB135－WB149．

［49］ Zhang Q S，McMechan G A．Common－image gathers in the incident phase－angle domain from reverse time migration in 2Delastic VTI media．Geophysics，2011b，76（6）：S197－S206．

［50］ Sava P C，Fomel S．Angle－domain common image gathers by wavefield continuation methods．Geophysics，2003，68（3）：1065－1074．

［51］ Sava P，Vasconcelos I．Extended imaging conditions for wave－equation migration．GeophysicalProspecting，2011，59（1）：35－55．