一种确定震源中心的方法：逆时成像技术（一）——原理与数值实验

许力生，杜海林，严 川，李春来

中国地震局地球物理研究所，北京 100081

1 引 言

地震活动与构造运动密切相关，因此，地震定位的问题一直以来都是一个非常重要的地震学问题．利用地震记录确定震源位置的工作最早可以追溯到1910 年盖戈的贡献［1－2］．后来普遍称为盖戈方法（Geiger－method）．盖戈方法的核心包括三部分，第一，把地震的震源位置与地震波走时的非线性关系线性化；第二，利用最小二乘方法求解此线性系统；第三，以线性系统和残差为正态分布作为前提构建解的置信区域．此后的许多工作都致力于这个方法的改进，但其精髓仍是盖戈方法的精髓［3－5］．由于其完整的求解及其评价体系，这类方法一直以来被广泛采用，因此，通常被称为标准定位方法（Standard location method）［6－8］．

然而，盖戈方法具有它的局限性．首先，非线性问题的线性化，除解的真确性依赖于初值的设定外（如果解的初值设定不合适，可能得不到“真解”），它还使解的精确性受到限制．地震的定位问题本身为非线性问题，非线性问题的线性化从根本上限制了解的精确性和准确性．当震中距较大和对解的精度要求不高时，线性化引起的问题并不明显，但是，当震中距较小且对解的精度提出高要求时，这种非线性问题的线性化引起的问题就会凸显出来［3－5，9－11］．事实上，为了减小线性化产生的误差，也有人做出过努力［6，12－13］．第二，利用最小二乘法求解，有时会导致错误的结果．利用最小二乘法求解的前提是观测误差呈正态分布，然而，实际上由于观测台站的不均匀分布以及观测资料的有限性，观测资料的观测误差很难满足正态分布的要求，因此，在这种情况下方程的最小二乘法解也很不准确．1930年Jeffreys最早认识到利用最小二乘方法定位时个别出格数据（Outlier）会使震源位置发生偏离问题，并首先采用逐渐丢弃残差较大的观测资料的方法改善解的准确性［11］．后来，更多的人也注意到这个问题，并采用称之为M－估计的计算技术解决这个问题［11，14－16］．M－估计属于稳健求解的技术，即根据残差大小反复调整各观测方程的权重，尽量使用残差小的数据，从而减小大残差资料对结果的影响［11，15，17］．第三，基于线性系统并以观测误差呈正态分布为前提建立的置信区域在很多情况下没有实际意义．有人明确指出，在通常的75%或者90%的置信水平上给出的置信区域可能非常大，且给出的定位结果很可能是错误的［3－4，18］．Evernden［19］批评指出，当台站数较少时，置信椭圆的大小已经完全失去了现实意义．Rowlett等［6］认为，由于所用的统计方法错误地假设具有大量的观测站且走时随震源位置线性变化，所以，标准定位方法给出的对定位结果的评价往往是错误的，甚至定位结果也是错误的．

由于几乎所有的常规定位工作中都采用盖戈类方法，所以，地震目录中地震位置往往具有很大的不确定性，甚至是错误的［20］．于是，出现了新的改善定位结果的方法，例如，主事件法［7－8，10，21－22］和双差法［20］．主事件法假设待定事件和主事件到观测点的射线路径相同或者相近，到时的相对变化仅是位置相对变化的结果，通过使相对走时误差最小确定待定事件的位置．因此，这种方法适用的前提是，地震分布的空间尺度远小于震源距，或者说仅适用于较小空间的震群（swarm）或震簇（cluster）的定位．双差法不要求主事件，但同样假设待定的两个事件（事件对）到观测点的射线路径相同或相近且观测到时的相对变化仅是位置相对变化的结果，通过使相对观测走时与相对理论走时的差的残差最小来确定待定事件的相对位置．由于事件对可以两两组合，因此，这种方法适用于地震“连续”分布的较大空间的地震定位．主事件方法的定位结果依赖于主事件的位置，而双差法的定位结果依赖于参与定位的所有地震的位置．

主事件法和双差法都是相对定位方法，而盖戈法及其衍生方法属于绝对定位方法．利用相对定位法的目的是消除或弱化介质模型的非参数化效应，而并不是真正让有误差的震源位置回归到它们真实的位置．相对定位的结果距离真实的位置究竟多远仍然取决于绝对定位的结果，因此，能否找到震源真实的位置归根到底取决于绝对定位．

绝对定位的质量依赖于方法，更依赖于包括观测点的空间分布、走时的测量误差等在内的观测资料的质量．观测点的空间分布往往不是人所能把握的（因为地震发生的位置是不可预知的），但是，走时测量的人为误差是可以减小的，走时的测量精度也是可以提高的．例如，波形的互相关技术就是一种提高测量精度、减小人为测量误差的方法［7，22－28］．数值实验表明，利用相关测量技术可以使测量精度达到采样间隔的十分之一［8］．然而，这种互相关技术应用的前提是波形具有一致性．如何突破这种技术的应用壁垒也是本研究的内容之一．

影响定位准确性的另一个重要因素是速度结构．无论是盖戈法还是双差法，其定位结果都强烈地依赖于使用的速度模型．要想得到好的定位结果，一个真实或者接近真实的模型是必要的．这一点需要其他研究提供保证．我们的定位工作都假设使用的速度模型是准确可靠的．

本文提出的绝对定位方法，避免问题的线性化，避免使用最小二乘法，避免使用评价解的统计方法，突破互相关技术的使用壁垒，旨在提高地震事件的定位精度和可靠性．需要说明的是，由于我们使用波形互相关确定到时并进一步确定震源位置，而不是直接读取初动到时后，再确定震源位置，所以，利用这种方法得到的震源信息是震源中心（hypocentroid）的信息，而不是传统的震源位置（hypocenter）的信息，二者之间的异同已经有人做过解释［20］．如果地震较小，震源近乎点源，那么，利用这种方法确定的位置与利用初动到时确定的结果一致；如果地震较大，震源具有一定的尺度，那么，利用这种方法确定的位置是震源中心的位置，不同于利用初动到时确定的结果．

2 原 理

根据位移表示定理，地震断层产生的地动位移可以表示为［29］：

式中，Σ表示断层面，ξ为断层面上任意一点，即：ξ∈Σ；Un（x，t）为场点（观测点）x处位移的n分量；Δui（ξ，τ）为断层面上的位错；cijpq（ξ）为ξ点介质的弹性模量；vj（ξ）为ξ点断层面法向的方向余弦；Gnp，q（x，t；ξ，τ）为格林函数Gnp（x，t；ξ，τ）对ξq的空间偏导数，而Gnp（x，t；ξ，τ）为τ时刻断层面上ξ点作用的p方向的单位集中力在x处t时刻产生的n方向的位移．

若只考虑震源中心（Hypocentroid），将地震断层的总体效应等价于此断层面上一点ξ0 在τ0时刻的震源效应，那么（1）式可改写为：

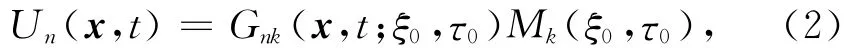
式中，Mk（ξ0，τ0）表示k类型震源机制的震源效应，Gnk（x，t；ξ0，τ0）表示k类型的震源在源点与观测点之间的介质效应．

现令震源的中心位于坐标原点，则（2）式可以改写为

（3）式中，x－ξ0 即为震源距，t－τ0即为走时．可以看出，如果在ξ0 点有地震记录Un（0，0），那么震源中心的位置就可以确定，此时，

在（4）式中，x，t是观测点位置与地震信号到达观测点的时刻，而ξ0，τ0是震源中心的位置（震源位置）和地震信号离开震源的时刻（发震时刻）．因此，如果让每个台站的记录信号“返回”源点，上述问题即可解决．

为了让各台站记录信号返回源点，我们仿照台阵的聚束技术，构建能量积分，

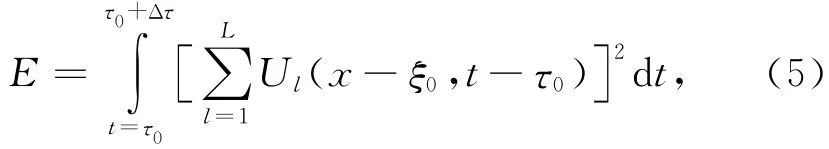
不难想象，当且仅当所有观测信号同时返回到源点时，上式取最大值，即

（6）式中，Emax表示最大能量，Δτ为震源持续时间（通常近似取直达波的第一个特征周期长度），L表示所用的记录数目．

为了求解（6）式，我们借用广义台阵成像技术［30－32］．不过，使用台阵技术的前提是待使用的波形具有一致性或相似性［33］．不但要求波形的形状相同，而且要求波形的振幅也相等．而（3）式中Un的大小与形状却随着Gnk或者Mk的变化而变化．一个现实的困难是不可能总是找到这样相同的记录．为了使所用波形资料具有“一致性”或“相似性”，须对原始信号进行如下处理：一、利用包络线技术使波形具有近似性；二、通过振幅归一使这些波形具有相同的振幅．具体做法如下：

令

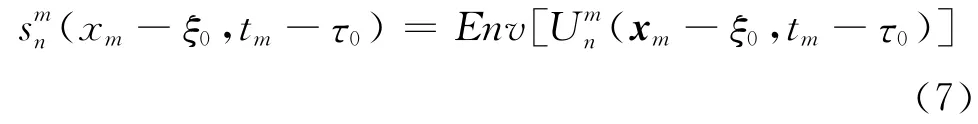
为观测点m的Un（x－ξ0，t－τ0）在时间窗［τ0，τ0＋Δτ］ 的包络线，并构造一个新信号

式中，＊表示褶积．然后通过如下运算进行振幅归一，

关于如何利用广义台阵技术对地震能量辐射源进行成像的原理和方法，在以前的工作中已经有比较系统的介绍［34］．为了方法的完整性，在此只做简要介绍．

设观测点的数目为M且每个观测点有N（N≤3）个分量，现定义

并计算积分

由（10）式不难想见，仅当ξ0 ＝xm和τ0＝tm时，（11）式取最大值．反之亦然．因此，只要找到（11）式的最大值，震源位置ξ0 和发震时刻τ0即可确定．注意：（6）式中的L＝M×N．

如何寻求（11）式的最大值，可能有很多途径，如遗传算法、粒子群算法等．但是，我们倾向于网格搜索方法，因为这种方法稳定可靠，不易陷入局部极小或极大，而且可以得到一个解的集合，这对于描述解的不确定性至关重要，而效率低的弱点在这样一个问题上并不明显．

在实际计算时，第一，根据实际情况（如：台网位置）给出震源位置的范围；第二，根据精度要求将给定区域网格化；第三，计算每个格点到观测点的距离；第四，根据格点到观测点的距离确定延迟时间；第五，利用延迟时间将观测波形进行延迟；第六，计算（11）式积分；最后，寻求（11）式积分的最大值，并利用此最大值确定震源位置集合ξι及其发震时刻集合τi．

不难发现，利用（11）式确定震源位置ξι和发震时刻τi的过程，相当于让各观测点信号从场点沿原路径“返回”震源中心位置的过程，也即“时光倒流”的过程，因此，此类技术通常被称为逆时成像技术（Time－reversal Imaging Technique or TRIT）［35］．

如上文所述，传统的定位方法利用统计方法描述解的不确定性［3－4］，而这样的误差估计在很多情况下没有实际意义［19，6］．在这里的方法中，为了描述解的不确定性，我们引入

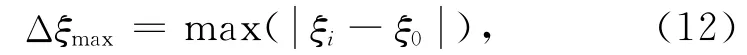
式中ξi为（11）式最大值Emax对应的点的集合（注意：满足（10）式的解不是唯一的），而ξ0 为ξι的平均值．可见，Δξmax反映了观测系统的空间分辨能力，不妨称为空间特征半径．类似地，我们用由ξi的发震时刻τi与ξ0 的发震时刻τ0的差的最大值Δτmax描述发震时刻的分辨能力，即

并称其为时间特征半径．可以想见，ξι集合的几何形状不但依赖于观测到时的拾取误差、介质的各向异性引起的到时误差等，也依赖于台站的几何分布，因此，Δξmax 和Δτmax实际上反映了观测系统的综合分辨能力．

盖戈类方法中多用拾取的观测到时与理论到时的差计算观测到时残差，而在我们的方法中，则利用聚束信号与观测信号通过互相关技术获取．从（10）式和（11）式可以看出，S0（ξ0，τ0）（聚束信号）是唯一的，是震源中心的标准信号，其前半周期信号的物理意义为震源的广义震源时间函数，相对而言，（7）式描述的是该台站的视震源时间函数．若各观测信号返回震源时可以表示为，则观测到时与理论到时的残差为

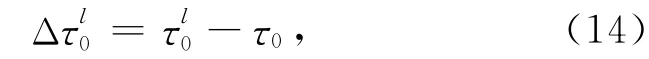
并令

与盖戈类方法利用统计方法评价解的不确定性不同，我们用Δξmax、Δτmax和Δ的组合描述ξ0 和τ0的不确定性．具体地，我们用

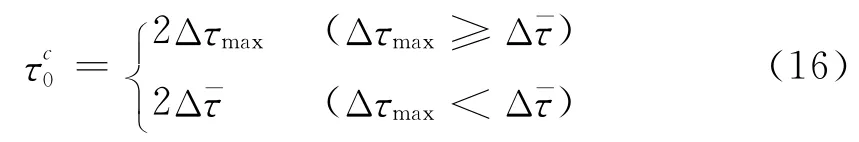
描述发震时刻的不确定性，而用

描述震源位置的不确定性．

3 数值实验

实验一：可行性测试

这个数值实验的目的是测试逆时成像方法的可行性，包括可靠性、稳定性和抵御噪声的能力．为此，我们首先构造一个地震台网，在台网内设定一次地震事件，计算设定事件在台网各台站的合成地震图，为合成地震图分别添加5%、10%、20%、30%的随机噪声，然后，利用这些记录确定设定地震的震源位置，最后，将利用不同噪声水平的观测记录确定的参数与设定参数进行比较．

如图1a所示，用7个台站构成一个小台网．在台网内近乎中心设定一地震事件，发震时刻设为2009年11月14日11点2分17．19秒，震中位置为35．0010°N，112．2097°E，震源深度为18．00km，震源机制被随意设置为走向90°、倾角45°、滑动角45°．为了保持与台站位置参数相同的精度，事件的位置参数也保留4位小数．

图1 数值实验使用的三种事件与台网分布顶端的分布用于实验一，其它两种用于实验二至五．Fig．1 Three varieties of the distribution of stations and events used in the numerical tests The top one is for the Test 1，and the others for the Tests 2to 5．

利用反射－折射率方法［36］，借用如表1 所示的地壳速度模型，设合成地震图的采样率为50Hz，计算得到台网各台站如图2a所示的合成地震图．同时，采用相同的速度模型计算震源深度范围和震中距范围分别为1至30km 和0至0．5°的走时表，使时间精度达0．02s，与观测资料的最小时间单位相当．

表1 数值实验使用的分层速度模型Table 1 Layered velocity model used in the numerical tests

图2 数值实验使用的合成信号（a）为图1中台站的合成地震图的垂直分量；（b）为30%噪声叠加后的合成地震图的垂直分量；（c）为利用（a）图直达P波初动后0．25s窗内信号构造的定位信号；（d）为找到震源中心位置时定位信号的状态，其中，最上面的信号为聚束信号．图中横坐标的0时刻指发震时刻，但（c）图中为了让局部信号清楚可见，0时刻设为第一个台站的到时．Fig．2 Synthetic recordings used in the numerical tests（a）are only the vertical components of the synthetic recordings for the stations shown in Fig．1；（b）are the same ones as shown on the upper－left but with 30%noise added；（c）are the signals built with envelops of the first 0．25s－windowed direct P shown on the upper－left，and（d）are the same ones as shown on the（c）but after the hypocentroid being found，the top one of which is the beam of the lower ones．The time 0sin subplots refer to occurrence times of the event，but that in the（c）refers to the arrival time at the first station only for clear presentation．

图2a仅显示了合成记录的垂直分量．考虑到这组P波信号的第一个周期大约为0．25s，震源的绝大部分能量出现在这个时间段，所以将信号窗的宽度设为0．25s，并截取这段信号；然后，通过希尔伯特变换得到相应包络线，并根据（8）式形成如图2c所示的合成信号．可以看出，尽管各台的原始记录的直达P波极性或形状并不相同，但经过变换形成的信号形状具有相当的一致性．

假定待确定的事件位于台网半径的1．5倍的范围内，并在0～30km 的深度之间，将给定的区域网格化，最初的格点之间的距离设为～600 m，然后，设为～120m，最后，设为～30m．通过三步搜索，如图2d所示，所有信号返回（位于同一时间起点），得到了如表2第一行所示的震源参数．

表2 实验1结果Table 2 Results of the Test 1

为了评估逆时成像方法对实际资料的适应能力，我们为如图2a 所示的合成地震图分别添加5%、10%、20%、30%的随机噪声，然后重复上面的步骤，得到的参数见表2中2—4行．需要说明的是，随着噪声水平的提高，有些台站的P波信号逐渐淹没在噪声当中，能够使用的台站数目逐渐减小．例如，如图2b所示，当噪声水平增加到30%时，台站DYT 和QST 的信号已不能使用．可见，噪声不但使可用的信号扭曲，而且使可用的台站数目减少．

为了定量认识在不同噪声水平情况下利用逆时成像方法得到的震源参数和给定震源参数之间的差异，我们分别计算了发震时刻之间的偏差、震中位置之间的偏差、震源深度之间的偏差以及震源位置之间的偏差，并展示在图3中．从图中可以看出，在5种情况下，发震时刻的最小偏差为0．05s，但不是无噪声情况下的结果；最大偏差为0．08s，但不是噪声水平最高情况下的结果；震中位置的最小偏差为20m，为无噪声情况下的结果；最大偏差为110m，也不是噪声水平最高情况下的结果；震源深度的最小偏差为20m，但不是噪声水平最低情况下的结果；最大偏差为150m，也不是噪声水平最高情况下的结果；震源位置的最小偏差为70m，不是无噪声情况下的结果；最大偏差为160m，也不是噪声水平最高情况下的结果．

图3 利用不同噪声水平记录确定的结果与给定结果的比较从左到右，依次为发震时刻（TC）、震中位置（EC）、震源深度（DC）和震源位置（SC）的偏差．Fig．3 Comparison of the results obtained using the recordings with different level of noises with the given onesFrom left to right are changes of the origin time（TC），epicenter（EC），depth（DC）and source（SC），respectively．

从以上结果可以看出，（1）无论噪声存在与否，定位结果总是与设定结果非常接近，例如，发震时刻、震中位置、震源深度和震源位置的最大偏差分别仅为0．08s、110m、150m 和160m；（2）噪声对结果有影响，但所受影响并不随噪声增加而增加，表明此方法具有较强的抗噪声能力．

实验二：台网几何对网内事件的影响测试

这个数值实验的目的是测试台站分布对台网内部事件的影响．为此，我们构造一个地震台网，并在台网内部设定10次地震事件；然后，计算设定事件在各台站的合成地震图；最后，利用合成地震图确定这些事件的位置，并将利用合成地震图确定的震源位置参数与设定震源位置参数进行比较．

构建如图1b所示的台网，在台网内部设定10次地震事件，事件参数如表3所示，地震事件的震源机制都设定为走向90°、倾角45°和滑动角45°．同样，基于如表1所示的速度模型，利用反射－折射率方法为各台站计算采样率为50Hz的合成地震图，并利用这些合成地震图进行定位．定位结果展示在表4中．

表3 网内事件设定位置Table 3 Locations of the given events within a network

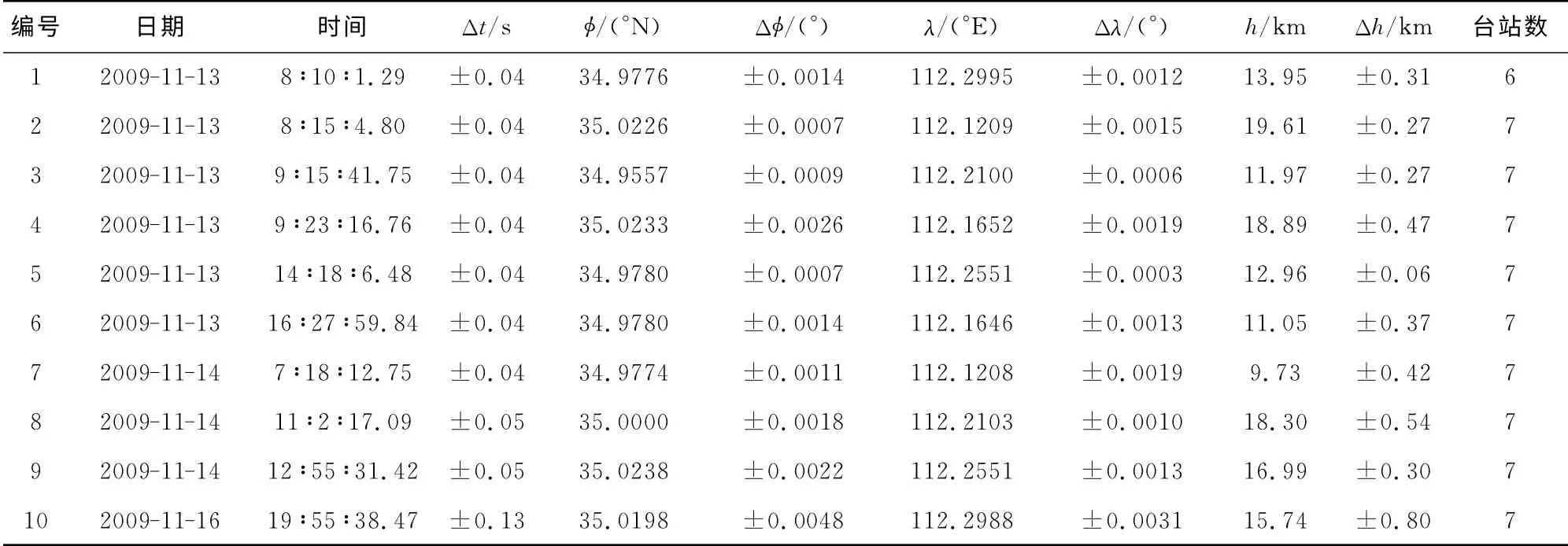
表4 实验二结果Table 4 Results of the Test 2

为了定量了解逆时成像方法对不同的网内地震事件的定位能力，评价反演得到的震源参数和给定震源参数之间的差别，我们分别计算了反演得到的发震时刻、震中位置、震源深度以及震源位置与其设定值之间的偏差．如图4（上）所示，在10次事件中，发震时刻的最小偏差和最大偏差分别为0．03s和0．1s；震中位置的最小偏差和最大偏差分别为20m和360m；震源深度的最小和最大偏差分别为20m和390m；震源位置的最小和最大偏差分别为50m和450m．平均地看，10次事件的发震时刻偏差仅0．06s，震中位置偏差仅90m，震源深度偏差仅150 m，震源位置偏差仅190m．

图4 实验二和实验三结果与给定结果的比较上图为网内事件的实验结果与给定结果的比较，下图为网际事件的实验结果与给定结果的比较（参看图3）．Fig．4 Comparison of the results obtained in Tests 2and 3with the given onesThe top one is for the events within the network，and the bottom is for the events on the margin of the network（see Fig．3）．

从以上结果可以看出，网内发生的地震事件的定位结果可能由于台网的几何形状的变化而变化，但这种影响十分有限．例如，在网内的10次地震事件中，最大的时间偏差、震中偏差、震源深度偏差和震源位置的偏差分别也仅为0．1s、360m、390m 和450m．

实验三：台网几何对网际事件的影响测试

这个数值实验的目的是测试台站分布对台网周边事件定位结果的影响．为此，我们构造一个地震台网，并在台网外围设定10次地震事件；然后，计算设定事件在各台站的合成地震图；最后，利用合成地震图确定这些事件的位置，并将利用合成地震图确定的震源参数与设定参数进行比较．

构建如图1b所示的台网，在台网外围设定10次地震事件，事件参数如表5所示．地震事件的震源机制同样都被设定为走向90°、倾角45°和滑动角45°．基于如表1所示的速度模型，利用反射－折射率方法为各台站计算采样率为50 Hz的合成地震图，并利用这些合成地震图进行定位．定位结果展示在表6中．

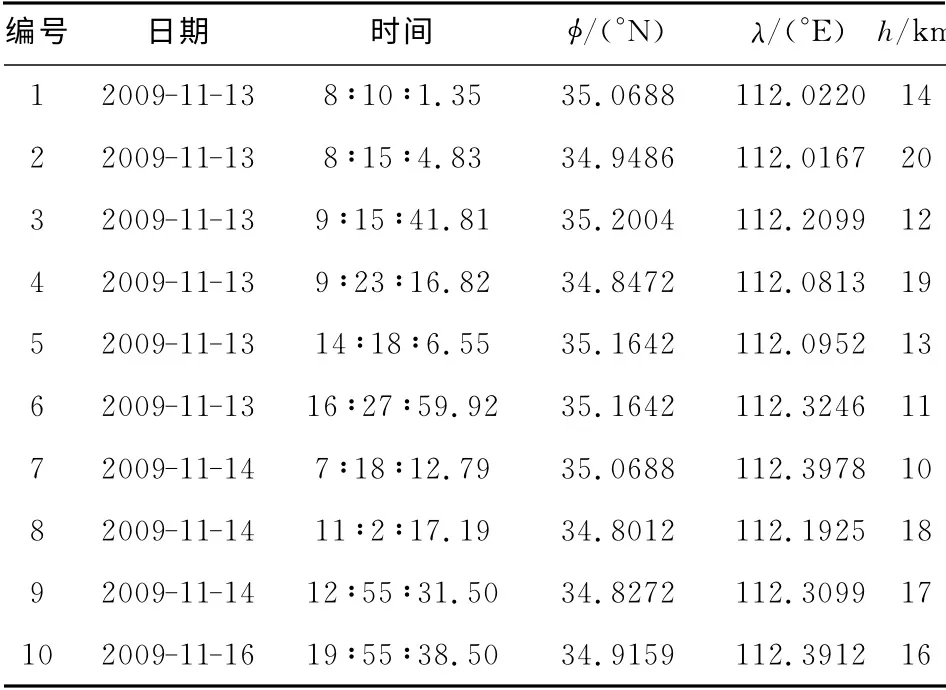
表5 网际事件设定位置Table 5 Locations of the given events on margin of the network

表6 实验三结果Table 6 Results of the Test 3

为了定量了解逆时成像技术对网际地震事件的定位能力，评价反演得到的震源参数和给定震源参数之间的差别，我们分别计算了反演得到的发震时刻、震中位置、震源深度以及震源位置与设定值之间的偏差．如图4（下）所示，在10次事件中，发震时刻的最小偏差和最大偏差分别为0．0s和0．13s；震中位置的最小偏差和最大偏差分别为50m 和450m；震源深度的最小和最大偏差分别为10m 和390m；震源位置的最小和最大偏差分别为100m 和550m．平均地看，10次事件的发震时刻平均偏差仅0．06s，震中位置平均偏差仅220m，震源深度平均偏差仅160m，震源位置平均偏差仅290m．

从以上结果可以看出，网际发生的地震事件的定位结果由于台网的几何形状的变化也发生了变化，但这种影响仍然是可以接受的，例如，在网际的10次地震事件中，最大的时间偏差、震中偏差、震源深度偏差和震源位置的偏差分别也仅为0．13s、450m、390m 和550m；同时，可以看到，与网内事件相比，网际事件受影响的程度在增加．例如，10次事件的发震时刻的平均偏差分别从0．03s增加到0．06s，震中位置的平均偏差从90m 增加到220m，震源深度的平均偏差从150m 增加到160m，震源位置的平均偏差从190m 增加到290m．可以预见，随着事件距台网的距离增加，定位偏差会越来越大．

实验四：网内事件震源机制和台网几何的影响测试

这个数值实验的目的是认识发生在台网内部的事件的震源机制变化与台网的几何形状变化的共同作用对定位结果的影响，因为，震源机制的变化会引起波形的变化，而波形的变化最终会对定位结果产生影响．为此，我们构造如图1b所示的地震台网，在台网内部设定10次地震事件，并设定每次事件具有4种代表性震源机制，前两种震源机制用断层面参数表示，后两种震源机制用矩张量表示．第一种：走向90°、倾角30°、滑动角90°；第二种：走向90°、倾角45°、滑动角45°；第三种：其矩张量为［1 1 1；1 1 1；1 1 1］；第四种：其矩张量解为［1 0 0；0 1 0；0 0 1］；然后，计算设定事件在各台站的合成地震图；最后，利用合成地震图确定这些事件的位置，并将利用合成地震图确定的震源位置参数与设定震源位置参数进行比较．

表7展示了第一种震源机制情况下的定位结果，图5a比较了定位结果与设定结果．从图中可以看出，在10次事件中，发震时刻的最小和最大偏差分别为0．04s和0．08s；震中位置的最小和最大偏差为20m和110m；震源深度的最小和最大偏差20m和270m；震源位置的最小和最大偏差分别为30m和270m．同时可以看出，10 次事件的发震时刻平均偏差仅0．06s，震中位置平均偏差仅60 m，震源深度平均偏差约110m，震源位置平均偏差约130m．

表7 实验4第一类震源机制实验结果Table 7 Results of the Test 4for the mechanism I

表8展示了第二种震源机制情况下的定位结果，图5b比较了定位结果与设定结果．在10次事件中，发震时刻的最小和最大偏差分别为0．03s和0．1s；震中位置的最小和最大偏差为20m 和360m；震源深度的最小和最大偏差20m 和390m；震源位置的最小和最大偏差分别为50m 和450m．同时可以看出，10次事件的发震时刻平均偏差仅0．06s，震中位置平均偏差仅90 m，震源深度平均偏差仅150m，震源位置平均偏差仅190m．

表8 实验4第二类震源机制实验结果Table 8 Results of the Test 4for the mechanism II

表9展示了第三种震源机制情况下的定位结果，图5c比较了定位结果与设定结果．在10次事件中，发震时刻的最小和最大偏差分别为0．01s和0．11s；震中位置的最小和最大偏差为10m 和190m；震源深度的最小和最大偏差50m 和500m；震源位置的最小和最大偏差分别为60m 和530m．同时可以看出，10次事件的发震时刻平均偏差仅0．05s，震中位置平均偏差仅90 m，震源深度平均偏差仅230m，震源位置平均偏差仅250m．

表9 实验4第三类震源机制实验结果Table 9 Results of the Test 4for the mechanism III

表10展示了第四种震源机制情况下的定位结果，图5d比较了定位结果与设定结果．在10次事件中，发震时刻的最小和最大偏差分别为0．04s和0．1s；震中位置的最小和最大偏差为30m 和70m；震源深度的最小和最大偏差10m 和310m；震源位置的最小和最大偏差分别为40m 和320m．同时可以看出，10 次事件的发震时刻平均偏差仅0．07s，震中位置平均偏差仅40m，震源深度平均偏差仅100m，震源位置平均偏差仅120m．

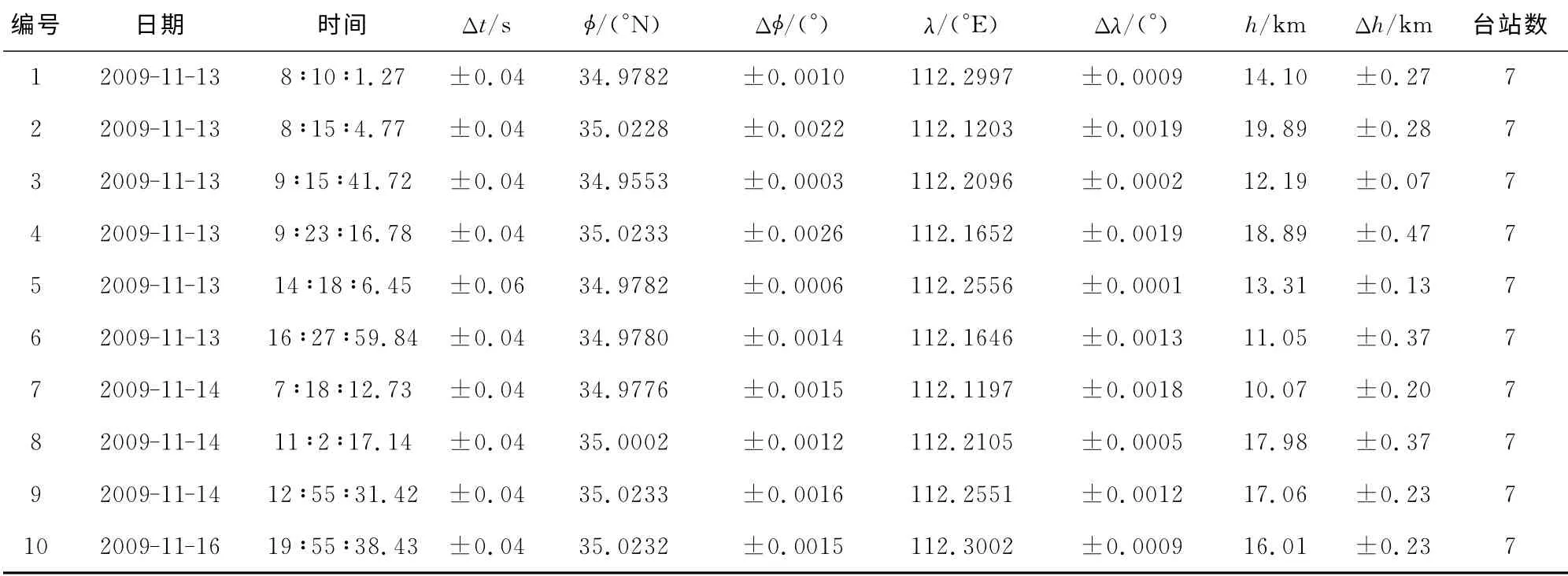
表10 实验4第四类震源机制实验结果Table 10 Results of the Test 4for the mechanism IV

图5 实验四结果与给定位置的比较．从上往下依次为第一类、第二类、第三类和第四类震源机制的网内事件的实验结果与给定位置的比较（参看图3）Fig．5 Comparison of the results obtained in Test 4with the given ones．From top to bottom are for the events within the network with mechanisms I，II，III and IV，respectively（see Fig．3）

从以上实验结果可以看出，震源机制的变化与台网几何的变化共同作用的确会对定位结果产生影响，这种共同作用有可能使得某些台站的地震波形无法使用（从表7—9 可以看出可用的台站数的变化），也可能使波形发生扭曲，进而影响定位结果，然而，这种影响也是有限的．例如，发震时刻的最大偏差为0．11s，震中位置的最大偏差为360m，震源深度的最大偏差为500 m，震源位置的最大偏差为530m．

实验五：网际事件震源机制与台网几何的影响测试

这个数值实验的目的是认识发生在台网外围事件的震源机制变化以及台网几何变化的共同作用对定位结果的影响．使用的台网和10次地震事件与实验三相同，使用的10 次地震的震源机制与实验四相同．

表11展示了第一种震源机制情况下的定位结果，图6a比较了定位结果与设定结果．从图中可以看出，在10次事件中，发震时刻的最小和最大偏差分别为0．0s和0．11s；震中位置的最小和最大偏差为20m和320m；震源深度的最小和最大偏差0m 和320m；震源位置的最小和最大偏差分别为110 m和380m．同时可以看出，10 次事件的发震时刻平均偏差为0．07s，震中位置平均偏差为170m，震源深度平均偏差为190m，震源位置平均偏差为270m．

表11 实验5第一类震源机制实验结果Table 11 Results of the Test 5for the mechanism I

表12展示了第二种震源机制情况下的定位结果，图6b比较了定位结果与设定结果．从图中可以看出，在10次事件中，发震时刻的最小和最大偏差分别为0．0s和0．13s；震中位置的最小和最大偏差为50m和450m；震源深度的最小和最大偏差10m和390m；震源位置的最小和最大偏差分别为100 m和550m．同时可以看出，10次事件的发震时刻平均偏差为0．06s，震中位置平均偏差为220m，震源深度平均偏差为160m，震源位置平均偏差为290m．

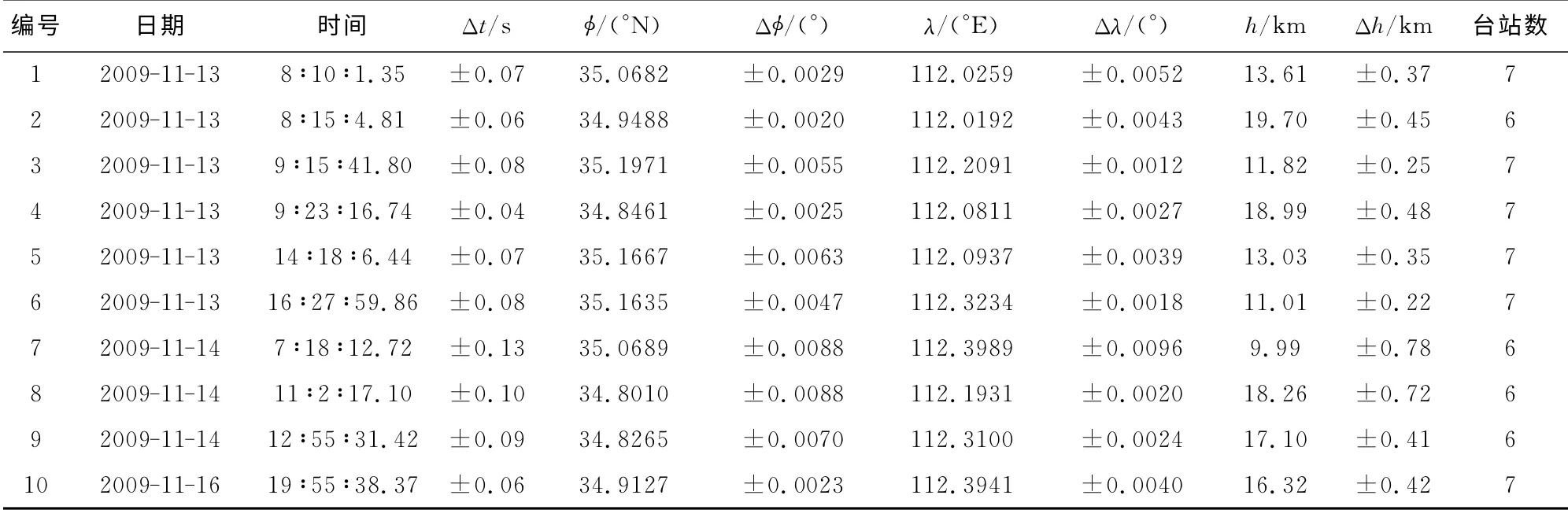
表12 实验5第二类震源机制实验结果Table 12 Results of the Test 5for the mechanism II

图6 实验五结果与给定结果的比较．从上往下依次为第一类（a）、第二类（b）、第三类（c）和第四类（d）震源机制的网际事件的实验结果与给定位置的比较（参看图3）Fig．6 Comparison of the results obtained in Test 5with the given ones．From top to bottom are for the events on the margin of the network with mechanisms I，II，III and IV，respectively（see Fig．3）

表13展示了第三种震源机制情况下的定位结果，图6c比较了定位结果与设定结果．从图中可以看出，在10次事件中，发震时刻的最小和最大偏差分别为0．03s和0．22s；震中位置的最小和最大偏差为60m 和980m；震源深度的最小和最大偏差为30m 和580m；震源位置的最小和最大偏差为60m和1140m．同时可以看出，10次事件的发震时刻平均偏差为0．09s，震中位置平均偏差为310m，震源深度平均偏差为230m，震源位置平均偏差为400m．

表13 实验5第三类震源机制实验结果Table 13 Results of the Test 5for the mechanism III

表14展示了第四种震源机制情况下的定位结果，图6d比较了定位结果与设定结果．从图中可以看出，在10次事件中，发震时刻的最小和最大偏差分别为0．0s和0．11s；震中位置的最小和最大偏差分别为20m 和440m；震源深度的最小和最大偏差分别为10m 和320m；震源位置的最小和最大偏差分别为110m 和560 m．同时可以看出，10 次事件的发震时刻平均偏差为0．06s，震中位置平均偏差为180m，震源深度平均偏差为150m，震源位置平均偏差为250m．

表14 实验5第四类震源机制实验结果Table 14 Results of the Test 5for the mechanism IV

从以上实验结果可以看出，与网内情况类似，震源机制的变化与台网几何的变化的共同作用对定位结果具有一定影响，而且的确与震源机制有关，例如，最大偏差都出现在第三类震源机制情况下，发震时刻的最大偏差达0．22s，震中位置的最大偏差达980m，震源深度的最大偏差达580m，震源位置的最大偏差达1140m．

与网内事件相比，网际事件的定位结果所受影响更大，例如，网内事件发震时刻的最大偏差为0．11s，而网际事件发震时刻的最大偏差为0．22s，网内事件的震中位置的最大偏差为360 m，而网际事件震中位置的最大偏差为980 m，网内事件的震源深度的最大偏差为500m，而网际事件的震源深度的最大偏差为580m，网内事件震源位置的最大偏差为530m，而网际事件震源位置的最大偏差为1140m．网际事件的偏差似乎是网内事件偏差的2倍．

4 讨 论

本文提出的逆时成像技术，由于没有采用线性近似，所以，规避了线性近似引入的误差．由于没有采用最小二乘法而是采用台阵的聚束技术求解，所以，即便观测误差不满足正态分布的条件，定位结果也不会受观测误差中所谓出格数据（outlier）的影响．聚束方法会自动排除出格数据，属于稳健求解的范畴．不同于盖戈类方法采用统计方法描述解的不确定性，逆时成像技术采用解集的特征半径和观测值的标准差描述解的不确定性．解的特征半径不但依赖于观测误差的分布特征，同时也依赖于观测点相对于事件的几何特性，所以，用解集的特征半径与走时标准差描述不确定性自动考虑了资料误差和台站几何等因素，给出的不确定性描述更具实际意义．另外，用聚束信号作为震源信号，并通过其与各台站信号的互相关确定走时残差，其结果更准确、更客观，减小了人为因素．需要说明的是，为了利用互相关技术，不得不将直达波的包络线当做视震源时间函数，不得不将聚束信号的前半周期当做震源时间函数，这是本方法中唯一产生近视误差的环节，但从实验结果可以看出，这点近似引起的误差可以忽略不计．

从实验一的测试结果可以看出，逆时成像方法具有较强的抗噪能力．噪声水平的增加可能降低资料的质量，也可能使可用的资料减少，但定位结果的偏差并不随噪声水平的增加而增加．

从实验二和三的测试结果可以看出，台网几何对定位结果会产生或多或少影响．正如所料，网内事件平均偏差小，而网际事件平均偏差大．不过，这些偏差都是可以接受的．例如，网内10次事件的发震时刻、震中位置、震源深度和震源位置平均偏差分别仅为0．06s，90 m，150 m 和190 m；又如，网际10次事件的发震时刻、震中位置、震源深度和震源位置平均偏差分别仅0．06s，220m，160m 和290m．网内事件的定位结果比网际事件的定位结果更准确．

从实验四和五的测试结果可以看出，虽然，震源机制的变化引起的波形变化对定位结果有影响，台网几何形状的变化对定位结果也有影响，而且这两种因素的影响在通常情况下都不能区分，但是，这种影响也是有限的、可接受的．例如，网内10×4次事件的发震时刻、震中位置、震源深度和震源位置平均偏差分别仅0．06s，70m，150m 和230m；又如，网际10×4次事件的发震时刻、震中位置、震源深度和震源位置平均偏差分别仅0．07s，220m，180m 和300m．同样，网内事件的定位结果好于网际事件的定位结果．

台网几何对定位结果有影响，震源机制对定位结果也有影响，而且，二者的影响通常是耦合的，时涨时消，不可区别而论．但是，从上文的数值实验可以看出，这类影响是可以接受的．当然，我们可以预料，随着事件距台网距离的增加，定位的偏差会越来越大．

影响定位结果的因素是多方面的，如观测到时的测量误差、方程系统产生的误差、台网几何引起的误差、介质各向异性引起的误差、速度模型不准确引起的误差等，但从根本上可以分为三类，一类是观测误差，例如：人为测量误差、噪声引起的误差、仪器计时误差以及台网几何引起的误差等；二类是方程系统产生的误差，例如：非线性问题的线性化引起的误差、求解方法带来的影响等；三类是速度模型的误差，例如：介质的各向异性引起的误差以及速度模型不准确引起的误差等．本文的逆时成像技术中互相关技术的使用大大减小了第一类误差，非线性系统的使用和聚束方法的使用彻底杜绝了第二类误差源，一定程度上弱化了第三类误差（介质各向异性引起的误差），且将观测误差的不确定性、速度模型的不准确性通过解集的特征半径与观测资料的标准差自动归算于解的不确定性．

一个准确可靠的定位结果来自于准确可靠的观测资料、严谨的方程系统、真实准确的速度模型以及恰当的求解方法．本文提出的逆时成像方法旨在获取准确可靠的资料、建立严谨的方程系统和选用恰当的求解方法，因此，定位结果是否准确可信还依赖于速度模型的使用．所以，要想获得真实可靠的定位结果，还需要一个真实可信的速度模型．

本文提出的逆时成像技术既适合于一维速度模型也适合于三维速度模型，但是，比较方便实用的还是一维速度模型，所以，本文的数值实验都是基于水平均匀速度分层模型．

另外，本文提出的方法既适合于直达P 波，也适合于直达S波，但是，我们强烈建议只使用直达P波，因为，与P波相比，直达S波总是或多或少受到P波后续尾波的干扰，即使使用互相关技术，获取的观测到时误差也较大［20，22］．

本文提出的逆时成像方法是一种非线性方法，和其它非线性方法一样，与线性方法相比，求解过程需要更多的时间，例如，本文涉及的每次定位过程在普通的个人计算机上需要大约30s．随着台网的增大或者格点的增加，需要的时间也要增加，不过，台网增大意味着震中距增大，震中距增大却意味着定位精度的降低，而定位精度的降低意味着格点的减少，格点的减少自然意味着机时的减少，所以，总能在计算效率和定位精度之间找到平衡点．实际上，我们将同样的方法也应用于全球事件的定位，所需时间约15s，因为，与小台网事件相比，全球地震定位精度要求更低．所以，本文提出的方法虽然效率较低，但却是一种旨在提高定位精度的小台网绝对定位方法．

需要说明的是，本文从原理上阐述了逆时成像方法的优点，也说明了其不足之处，同时，利用尽可能多的数值实验验证了它的稳定性、可行性以及抵御噪声的能力，也完成了对网内、网际事件近乎实际情况的定位能力的测试．然而，为了更加充分地论证盖戈类方法和逆时成像方法的优缺点，还需要一系列比较系统的、有针对性的数值试验的测试，比如，对出格数据的容忍能力测试、对解的不确定性的实际意义的测试等．此工作即将完成，待另文讨论．

5 结 论

本文提出的逆时成像震源中心定位技术旨在提高地震台网绝对定位的精度．采用互相关技术，提高了观测到时测量的精确性、准确性和客观性；采用包络线技术，拓展了互相关技术的应用范围；采用直达波包络线直接积分求解技术，绕开了标准定位方法中的线性化过程、求解到时残差最小二乘解的过程以及解的不确定性的统计评价过程，消除了线性化误差，克服了最小二乘解对出格数据敏感的缺点，抛弃了统计评价体系．近乎实际情况的数值实验表明，逆时成像技术是可靠稳定的，具有较强的抵御噪声的能力．虽然，台网的几何形状和/或地震事件的震源机制对定位结果有影响，但对网内和网际事件而言，这种影响是有限的、可以接受的．

（References）

［1］ Geiger L． Herdbestimmtung bei Erdbeben ans den Ankunftszeiten．K．Gesel．Wiss．Gott．，1910，331－349．Geiger L．Probability method for the determination of earthquake epicenters from the arrival time only．Bull．St．Louis．Univ．，1912，8（1）：60－71．

［2］ Bratt S R，Bache T C．Locating events with a sparse network of regional arrays．Bull．Seism．Soc．Am．，1988，78（2）：780－798．

［3］ Flinn E A．Confidence regions and error determinations for seismic event location．Rev．Geophys．，1965，3（1）：157－185．

［4］ Buland R．The mechanics of locating earthquakes．Bull．Seism．Soc．Am．，1976，66（1）：173－187．

［5］ Jordan T H，Sverdrup K A．Teleseismic location techniques and their application to earthquake clusters in the South－Central Pacific．Bull．Seism．Soc．Am．，1981，71（4）：1105－1130．

［6］ Rowlett H， Forsyth D W． Recent faulting and microearthquakes at the intersection of the Vema Fracture Zone and the Mid－Atlantic Ridge．J．Geophys．Res．，1984，89（B7）：6079－6094．

［7］ Ito A． High resolution relative hypocenters of similar earthquakes by cross－spectral analysis method．J．Phys．Earth．，1985，33（4）：279－294．

［8］ Ito A．Earthquake swarm activity revealed from highresolution relative hypocenters－clustering of microearthquakes．Tectonophysics，1990，175（1－3）：47－66．

［9］ Smith E G C．Scaling the equations of condition to improve conditioning．Bull．Seism．Soc．Am．，1976，66（6）：2075－2076．

［10］ Spence W．Relative epicenter determination using P－wave arrival－time differences．Bull．Seism．Soc．Am．，1980，70（1）：171－183．

［11］ Anderson K R． Robust earthquake location using Mestimates．Phys．EarthPlanet．Interiors，1982，30（2－3）：119－130．

［12］ Thurber C H．Nonlinear earthquake location：theory and examples．Bull．Seism．Soc．Am．，1985，75（3）：779－790．

［13］ Pavlis G L． Appraising earthquake hypocenter location errors：a complete，practical approach for single－event location．Bull．Seism．Soc．Am．，1986，76（6）：1699－1717．

［14］ Bolt B A．The revision of earthquake epicentres，focal depths and origin－times using a high－speed computer．Geophys．J．R．Astron．Soc．，1960，3（4）：433－440．

［15］ Anderson K R．Epicentral location using arrival time order．Bull．Seism．Soc．Am．，1981，71（2）：541－546．

［16］ Chave A D，Thomson D J，Ander M E．On the robust estimation of power spectra，coherences，and transfer functions．J．Geophys．Res．，1987，92（B1）：633－648．

［17］ Andrews D F． A robust method for multiple linear regression．Technometrics，1974，16（4）：523－531．

［18］ Lilwall R C，Francis T J G．Hypocentral resolution of small ocean bottom seismic networks．Geophys．J．R．Astron．Soc．，1978，54（3）：721－728．

［19］ Evernden J F．Precision of epicenters obtained by small numbers of world－wide stations．Bull．Seism．Soc．Am．，1969，59（3）：1365－1398．

［20］ Waldhauser F， Ellsworth W L． A Double－difference earthquake location algorithm：Method and application to the Northern Hayward fault，California．Bull．Seism．Soc．Am．，2000，90（6）：1353－1368．

［21］ Geller R J，Mueller C S．Four similar earthquakes in central California．Geophys．Res．Lett．，1980，7（10）：821－824．

［22］ Deichmann N，Garcia－Fernandez M．Rupture geometry from high－precision relative hypocentre locations of microearthquake clusters．Geophys．J．Int．，1992，110（3）：501－517．

［23］ Poupinet G，Ellsworth W L，Fréchet J．Monitoring velocity variations in the crust using earthquake doublets：an application to the Calaveras fault，California．J．Geophys．Res．，1984，89（B7）：5719－5731．

［24］ Scherbaum F，Wendler J．Cross spectral analysis of Swabian Jura （SW Germany）three－component microearthquake recordings．J．Geophys．，1986，60（2）：157－166．

［25］ Spudich P，Bostwick T．Studies of the seismic coda using an earthquake cluster as a deeply buried seismograph array．J．Geophys．Res．，1987，92（B10）：10526－10546．

［26］ Frémont M J，Malone S D．High precision relative locations of earthquakes at Mount St．Helens， Washington．J．Geophys．Res．，1987，92（B10）：10223－10236．

［27］ Console R，Di Giovambattista R．Local earthquake relative location by digital records．Phys．Earth．Planet．Inter．，1987，47：43－49．

［28］ Pechmann J C，Thorbjarnardottir B S．Waveform analysis of preshock－mainshock－aftershock sequence in Utah．Bull．Seism．Soc．Am．，1990，80（3）：519－550．

［29］ Aki K，Richards P G．Quantitative Seismology．San Francisco：W．H．Freeman and Company，1980：38－40．

［30］ Krüger F，Ohrnberger M．Tracking the rupture of theMW＝9．3 Sumatra earthquake over 1150 km at teleseismic distance．Nature，2005，435（7044）：937－939．

［31］ Ishii M，Shearer P，Houston H，et al．Extend，duration and speed of the 2004Sumatra－Andaman earthquake imaged by the Hi－Net array．Nature，2005，435（7044）：933－936．

［32］ Xu Y，Koper K D，Sufri O，Zhu L P．Rupture imaging of theMw7．9 12 May 2008 Wenchuan earthquake from back projection of teleseismic P waves．Geochem．Geophys．Geosyst．，2009，10（4）：Q04006．

［33］ 杜海林．2004年苏门答腊—安达曼大地震能量辐射源的时间域台阵技术分析［硕士论文］．北京：中国地震局地球物理研究所，2007．

Du H L．Analysis of the energy radiation sources of the 2004 Sumatra－Andaman earthquake using time－domain array techniques（in Chinese）［Master′s thesis］．Beijing：Institute of Geophysics，China Earthquake Administration，2007．

［34］ Rost S， Thomas C． Array seismology： methods and applications．Rev．Geophys．，2002，40（3）：2－1－2－27．

［35］ Larmat C，Montagner J P，Fink M，et al．Time－reversal imaging of seismic sources and application to the great Sumatra earthquake．Geophys．Res．Lett．，2006，33（19）：L19312．

［36］ Kennett B L N．Seismic Wave Propagation in Stratified Media．Cambridge：Cambridge University Press，1983：1－342．