移动平均法在减小供应链牛鞭效应中的有效性分析

□文/肖亚明

（安徽工业大学研究生学院 安徽·马鞍山）

一、模型构建

为了便于研究，首先构建一个简单的二级供应链系统，我们做如下假设：

*供应链上有2 个企业，它们分别是1 个零售商和1 个制造商；

*零售商直接满足顾客需求，没有运输延迟时间；

*零售商不准缺货，制造商的生产能力无限；

*订单延迟以及运输延迟时间均为1 周，制造商生产周期为2 周；

*各节点企业安全库存以及初始库存都为100，单位件；

*各节点企业均采用安全库存策略；

*模拟周期为50 周；

*各个周期的订货量以及发货量大于或等于零；

*单位库存以及订货费用均为1 元，单位缺货费用为2 元。

相关说明：设定第三个假设的意义在于保证零售商与制造商的总时间延迟相同，目的是为了在时间延迟相同的条件下分析市场需求在向上传递过程中的放大现象。零售商的订单延时与制造商运输延迟时间之和为2 周，这就意味着零售商从发出订单到最后收到货物实际上经过了2 周的延迟时间。制造商的生产周期也为2 周，表示制造商从制定生产计划到货物进入仓库成为库存的时间也为2 周。这就剔除了因为延迟时间不同对需求放大所造成的影响。

该模型中相关变量以及公式定义如下：

*市场需求：市场需求是用MATLAB 随机函数产生的一组均匀分布随机变量。具体公式如下：NORMINV（RAND（）），80，10）

*市场销售=MIN（上周库存+本周到货，市场需求）

*订货量=MAX（（安全库存-库存）/库存调整时间+本周需求，0），初始值为0

*本周需求=下游企业订货量（延迟时间以前）

*库存量=上周库存量+本周到货-本周发货量，各节点企业库存初始值都为100

*本周到货=上游发货量（运输延迟时间以前）

*发货量=MAX（MIN（上周库存+本周到货，本周需求+上周缺货），0）

*缺货量=本周需求-本周发货量

*生产需求=（安全库存-库存）/库存调整时间+本周需求

说明：上述公式中“本周到货”是由上游供应商的“发货量”经过运输延迟时间后传入的，它们在数值上是相等的。“本周需求”是由下游需求方的“订货”经过订货延迟传入的，它们在数值上也是相等的。

二、模型仿真

首先针对上述模型，运用matlab 进行仿真，得出牛鞭效应图，如图1所示。（图1）

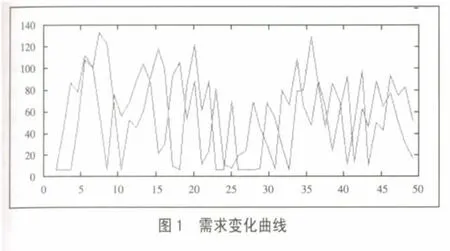
图1说明：黑线为市场需求；红线为零售商需求；蓝线为制造商生产需求。

当需求出现波动时，运用matlab 仿真，得出如下牛鞭效应图，如图2所示。（图2）

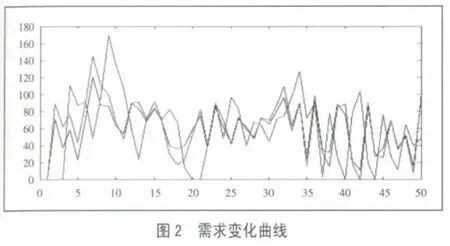
图2说明：黑线为市场需求；红线为零售商需求；蓝线为制造商生产需求。

比较图1和图2可以看出，当需求出现波动时，制造商的生产需求峰值达到了170，牛鞭效应加剧。

三、在市场预测环节加入移动平均法，分析其牛鞭效应情况

移动平均法是取预测对象最近一组历史数据的平均值作为预测值的方法。这种方法不是仅取最近一期的历史数据作为下一期的预测值，而是取最近一组历史数据的平均值作为下一期的预测值，这一方法使近期历史数据参与预测，使历史数据的随机成分有可能互相抵消，平均值所含的随机成分就会相应减少。

移动平均法的“平均”是指对历史数据的“算术平均”，而“移动”是指参与平均的历史数据随预测值的推进而不断更新。当一个新的历史数据进入平均值时，要剔除原先参与预测平均的最陈旧的一个历史数据，并且每一次参与平均的历史数据的个数是相同的。

其计算公式为：Ft+1=

其中，F 表示预测值，X 表示历史数据，n表示参与移动平均的数据个数。

为了便于研究对比，在此取前面的研究数据运用移动平均法进行预测，仿真结果如下：

运用matlab 对几个参数进行仿真，得出牛鞭效应曲线，如图3所示。（图3）

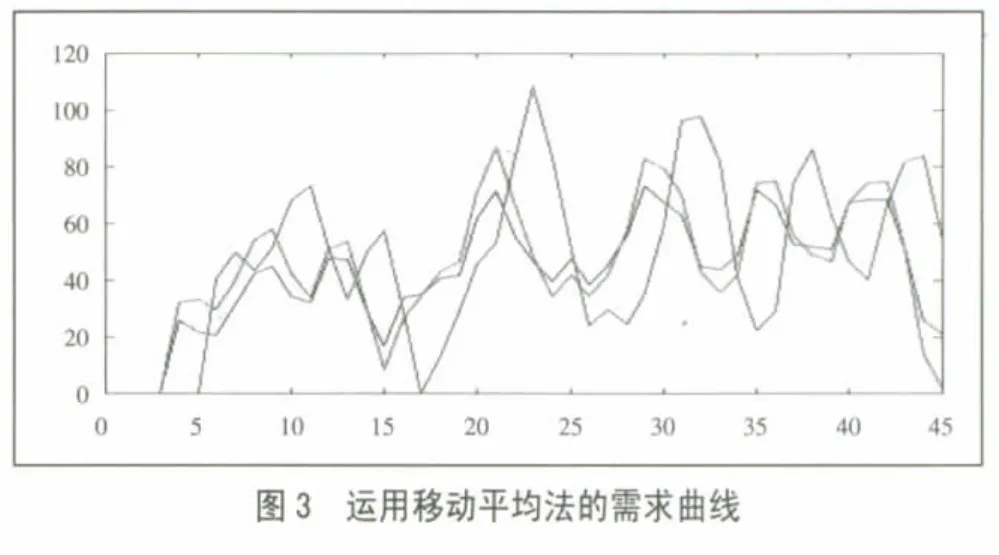
图3说明：黑线为市场需求；红线为零售商需求；蓝线为制造商生产需求。

根据仿真结果我们可以看到使用移动平均法后，订货以及库存波动的趋势都有所减弱，对照图1与图3我们可看到制造商生产需求的峰值从140 减少到115，振动明显减弱，有效地减小了系统的牛鞭效应。据此可以看出，在需求预测环节，采用移动平均法能够减小牛鞭效应，有效地增加了供应链系统的稳定性。

当需求出现波动时，使用移动平均法的有效性研究。针对需求突变的情形，现使用移动平均法对输入变量进行仿真，仿真结果如图4所示。（图4）

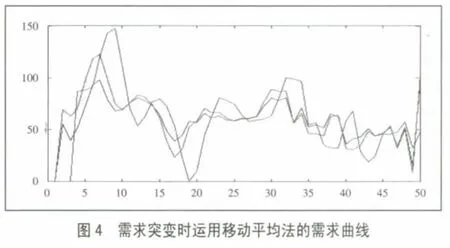
图4说明：黑线零售商库存；红线为制造商库存；蓝线为制造商生产需求。

比较图2及图4我们可以看出，在需求出现突变也即波动时，图2振动加剧也即系统的不稳定性明显加剧，牛鞭效应增大，制造商的最大需求量达到了172。在使用移动平均法对需求进行预测后，观察图4，系统振幅减弱，需求曲线振动减小，制造商的最大需求也减小到了150 以下。据此可以看出，在需求预测环节，即使出现需求波动，采用移动平均法也能够减小牛鞭效应，有效地增加了供应链系统的稳定性。■