考虑固液范德华力作用的微圆管流动数学模型

王小锋，朱维耀，邓庆军，隋新光，娄 钰，张雪龄

（1．北京科技大学土木与环境工程学院，北京 100083； 2．大庆油田有限责任公司第一采油厂，黑龙江大庆163453）

考虑固液范德华力作用的微圆管流动数学模型

王小锋1，朱维耀1，邓庆军2，隋新光2，娄 钰1，张雪龄1

（1．北京科技大学土木与环境工程学院，北京 100083； 2．大庆油田有限责任公司第一采油厂，黑龙江大庆163453）

细小孔隙喉道下流体流动呈非线性流动，达西定律不适用，非线性流动的机理认识不清．在现有微尺度流动实验和理论基础上，分析影响多孔介质中流体流动的微观力种类和作用范围及对流动的影响，建立考虑固液间范德华力的圆管流动数学模型．结果表明：对比泊肃叶流动下的速度分布和平均流量，随着微管尺寸的减小，固液间的范德华力作用增大，流体在微管内的流动规律影响也增大，因此固液间范德华力作用在细小孔隙流动中不可忽略．

多孔介质；微观力；范德华力；速度分布；平均流量

0 引言

随着微机械系统的发展，研究人员对于微尺度下的流动问题有一定认识，油层岩石孔隙尺寸属于微尺度范畴，因而，进一步研究微尺度下流体的运动规律对于油田开发具有重要意义［1—5］．Gad E H在实验中观察到流动的微尺度效应；Pfahler J等进行微观流动实验，研究表明流体流动偏离N—S方程预测的理论值［6—7］；Li Qingren，Qu Weilin等在高为14．1，28．2，40．5μm的硅槽中进行水和KCl水溶液的流动实验，研究表明水的极性是产生微尺度下流动偏离N—S方程的原因［8—9］；武东健等［10］建立水在固壁边界条件和滑流边界条件下的阻力因数和速度分布模型，研究表明流体在直径小于几百微米的微管中流动特性，用经典流体理论解释圆微管中的牛顿流体的层流和电解质流动，实验与理论出现偏差［11—16］，发现管壁与流体之间的微观力作用是造成这一结果的主要原因［13］．

目前，考虑微观力作用的微管流动模型鲜见，因此，笔者分析微管内的微观力作用，研究范德华力对流体在微圆管流动产生的影响，建立固体管壁与流体间范德华力作用下的速度和平均流量模型，并对微圆管内流体的流动进行模拟和分析，为认识和探究多孔介质细小孔喉内流体的流动规律提供参考．

1 多孔介质中的微观力

流体在多孔介质的孔隙和喉道内流动时，由于孔喉的特征尺寸微小，流体流动受管壁与流体间微观力的影响增大，微观力不可忽略．微观力主要包括范德华力、静电力、表面张力等．

分子间的范德华力包括3个部分，即取向力、诱导力和色散力．取向力是指分子永久偶极矩间的相互作用；诱导力是指分子被电场作用产生极化而形成的偶极矩与永久偶极矩间的相互作用；色散力是指分子瞬时偶极间的相互作用．黏度是分子间范德华力的表征，分子间范德华力越大，黏度越大，分子间范德华力越小，黏度越小．

静电力是带电分子或粒子间的作用力，大小与距离的平方成反比，作用距离比范德华力长，在距离小于0．1μm时最为重要，在10μm时仍有影响．在静电力作用下，壁面与电解质溶液形成双电层，当溶液受到压力差驱动时，双电层内的净电荷随溶液运动，产生流动诱导电场，电场作用使微通道双电层上的净电荷向溶液流动的反方向运动，使溶液的正向流速减慢．

表面张力是由液体表面层分子引力不均衡引起的．液体界面的分子与液体本体内的分子所受力不同，表层分子比内部水分子储存多余的自由能，如果要把内部的水分子举升到水表面上，需要付出能量做功，能量转化为表面自由能．表面自由能有趋于最小的趋势，液体表面有自动缩小的趋势，收缩力即为表面张力．表面张力与温度、界面性质有关，油层中流体的表面张力影响油层中流体在岩石表面上的分布，对孔隙中毛管力的大小和方向也有影响，表面张力越大，毛管力越大，也影响流体在多孔介质中的渗流规律．

2 微圆管流动数学模型

2．1 假设条件

假设有水相流体在水平放置的微圆管内定常流动，忽略重力影响（见图1）．图1把x轴设在管轴上，令r表示由轴心向外度量的径向坐标，周向和径向的速度分量为0，微圆管的半径为R，平行于管轴方向的速度分量为ux（仅仅依赖于r），沿x方向上的压力梯度为常数，微圆管的长度为L，入口压力为p1，出口压力为p2，考虑固体壁面与流体间的范德华力作用．

图1 水平放置的微圆管流体流动示意Fig．1 The scheme of fluid in the horizontal placement micro tube

2．2 黏度方程

当水相在微圆管内流动时，流体与管壁间的范德华力作用使流体间的分子引力增大，因而流体黏度μ增大，假设流体黏度由2部分组成：一是不考虑固液范德华力作用时流体的黏度μ0；二是考虑固液间长程范德华力后增大的黏度，所以流体黏度表示为

式（1—4）中：b为黏度增加因数；x为到固体壁面的距离；μ1、α1、Ι1分别为水分子的偶极距、极化率和电离能；μ2、α2、Ι2分别为固体表面分子的偶极距、极化率和电离能；Aw、As分别为水和固体管壁的哈默克常数；βw、βs分别为水和管壁的范德华力作用因子；Mw、Ms分别为水和管壁的相对分子质量；ρw、ρs分别为水和管壁的密度；NA为阿伏伽德罗常数；k为波尔兹曼常数．

2．3 运动方程

柱坐标系下N—S方程为

式中：uθ为周向分速度；fx为x方向惯性力；ρ为管内流体密度．

流体在管内定常流动，周向和径向的速度分量为0，速度u仅仅依赖于r，因而

边界条件为

结合式（1—7），推导可得微圆管内水相速度u为

由式（8）积分求得通过微圆管截面的平均流量Q，即

若不考虑固体管壁与流体间范德华力作用时，即AS＝Aw，代入式（9），则式（9）退化为泊肃叶定律形式，即

3 实例分析

3．1 不同管径下速度分布

根据推导的微圆管内流体的速度分布模型，当流体黏度μw＝1mPa·s，压力梯度dp／dx＝1×105Pa／m，流体的Hamaker常数Aw＝4．2×10—20J，管壁的Hamaker常数分别取As＝3．6×10—20J，As＝4．2× 10—20J，As＝4．8×10—20J时，模拟流体在不同固液范德华力作用下的速度与泊肃叶流动下的速度，管径分别取1，100μm，模拟结果见图2．

由图2可知，当微圆管半径在1～10μm时，如果考虑固体管壁与流体间的范德华力作用，那么微管内流体的速度分布明显低于泊肃叶流动，管径越小，与泊肃叶流动之间的速度偏离程度越大，固壁面的Hamaker常数越大，与泊肃叶流动的速度偏离程度越大；随着管径的增大，分子作用的影响逐渐减小，流体速度也越接近于泊肃叶流动，当管径达到100μm时，偏离程度已经较小．管径小于10μm时，速度偏差较大，不能忽略固液间范德华力作用的影响．

3．2 不同管径下平均流量

根据推导的平均流量模型，当流体黏度μw＝1mPa·s，压力梯度dp／dx＝1×105Pa／m，流体的Ha—maker常数Aw＝4．2×10—20J，管壁的Hamaker常数分别取As＝3．6×10—20J，As＝4．2×10—20J，As＝4．8×10—20J时，模拟流体在不同固液范德华力作用下的平均流量与泊肃叶流动下的平均流量，管径分别取0．1～1．0，10～100μm，模拟结果见图3．

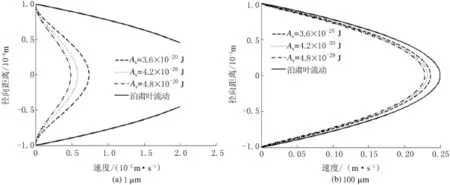
图2 范德华力作用下不同管径的速度分布Fig．2 Velocity distribution under different diameters considering van der Waals forces

图3 范德华力作用下不同管径的平均流量变化曲线Fig．3 Velocity distribution under different diameters considering micro force

由图3可知，当管径在0．1～1．0μm时，如果考虑固体管壁与流体间的范德华力作用，那么微管内流体的平均流量明显低于泊肃叶流动，管径越小，与泊肃叶流动之间的平均流量偏离程度越大，固壁面的Hamaker常数越大，与泊肃叶流动的平均流量偏离程度越大；随着管径的增大，范德华力作用的影响逐渐减小，流体平均流量越接近于泊肃叶流动，当管径达100μm时，偏离程度已经较小，当管径达10～100μm时，几乎没有偏离．管径小于10μm时，平均流量偏差较大，不能忽略固液间范德华力作用的影响．

4 结论

（1）建立考虑固液间范德华力作用的微圆管流动数学模型，推导牛顿流体在微圆管内的速度分布和平均流量模型．

（2）考虑管壁与流体之间的范德华力作用时，对比泊肃叶流动下的流体速度和平均流量，半径越小，与泊肃叶流动之间的偏离程度越大，管径在0．1～1μm时，偏离程度很大；半径越大，范德华力作用的影响逐渐减弱，速度和平均流量越接近于泊肃叶流动，管径在10～100μm时，偏离程度较小，分子作用几乎没有影响．

（3）把岩石孔隙喉道抽象为微圆管，当多孔介质的孔隙喉道尺度小于10μm时，固液间范德华力作用明显，不可忽略；当孔隙喉道尺度大于10μm时，固液间范德华力作用不明显，可忽略不计．

参考文献：

［1］ 刘中春，侯吉瑞，岳湘安．微尺度流动界面现象及其流动边界条件分析［J］．水动力学研究与进展，2006，21（3）：339—346．Liu Zhongchun，Hou Jirui，Yue Xiangan．Nterfacialphenomena inm icro—scale flowing and its flowing boundary condition［J］．Journal of Hydrodymics，2006，21（3）：339—346．

［2］ 凌智勇，丁建宁，杨继昌，等．微流动的研究现状及影响因素［J］．江苏大学学报：自然科学版，2002，23（6）：1—4．Ling Zhiyong，Ding Jianning，Yang Jichang，et al．Research advance in microfluid and its influencing factors［J］．Journal of Jiangsu University：Natural Science，2002，23（6）：1—4．

［3］ 张颖，王蔚，田丽，等．微流动的尺寸效应［J］．微纳电子技术，2008，45（1）：33—36．Zhang Ying，Wang Wei，Tian Li，et al．Scaling effect of micro fluidic systems［J］．Mems Device ＆Technology，2008，45（1）：33—36．

［4］ 张继红，王江，赵丽娟，等．单相液体在多孔介质中的电动渗流特性［J］．大庆石油学院学报，2006，21（1）：24—26．Zhang Jihong，Wang Jiang，Zhao Lijuan，et al．Characteristics of electrodynamic seepage flow of one—phase fluid in porous media［J］．Journal of Daqing Petroleum Institute，2002，26（1）：24—26．

［5］ 马贵阳，杜明俊，李丹．岩石部分润湿对水驱油藏微观相态分布的影响［J］．大庆石油学院学报，2006，21（1）：46—50．Ma Guiyang，Du Mingjun，Li Dan．Partial wet of rock impacts on the distribution of water drive reservoir microscopic phase［J］．Journal of Daqing Petroleum Institute，2011，35（2）：46—50．

［6］ Gad E H．The fluid mechanics of microdevices—the freeman scholarlecture［J］．J．of Fluids Engineering，1999，12（1）：5—33．

［7］ Pfahler J，Harley J，Bau H．Liquid transport in micronand submicron channels［J］．Sensors and Actuators，1990，21（23）：431—434．

［8］ Li Qingren，Qu Weilin，Li Dongqing．Interfacial electrokinetic effectson liquid flow in microchannels［J］．Int．J．of Heat and Trans—fer，2001，44（3）：3125—3134．

［9］ Qu Weilin，Mara G M，Li Dongqing．Pressure driven flows in trape—zoidal silicon micro channels［J］．Int．J．of Heat and Transfer，2000，43（4）：353—364．

［10］ 武东健，贾建援，王卫东．微细管道内的流体阻力分析［J］．电子机械工程，2005，21（4）：38—40．Wu Dongjian，Jia Jianyuan，Wang Weidong．Analysis of flow resistance of water in micro channels［J］．Electro Mechanical Engineer—ing，2005，21（4）：38—40．

［11］ Carolyn L R，Li Dongqing．Improved understanding of the effect of electrical double layer on pressure—driven flow in micro channels ［J］．Analytica Chimica Acta，2005，53（1）：15—23．

［12］ Yakov I，Rabinovich．Capillary forces between surfaces with nanoscale roughness［J］．Advances in Colloid and Interface Science，2002，9（6）：213—230．

［13］ Warrier M，Rai A，Schneider R．A time dependent model to study the effect of surface roughness on reactive—diffusive transport in porous media［J］．Journal of Nuclear Materials，2009，39（10）：203—206．

［14］ Anikin Y A，Derbakova E P．Computing of gas flows in micro and nanoscale channels on the base of the boltzmann kinetic equation ［J］．Procedia Computer Science，2010，53（1）：735—744．

［15］ Yakov I R，Joshua J A，Madhavan S E．Capillary forces between surfaces withnanoscale roughness［J］．Advances in Colloid and In—terface Science，2002，9（6）：213—230．

［16］ Celata G P，Cumob M，Mcphaila S，et al．Characterization of fluid dynamic behavior andchannel wall effects in microtube［J］．Inter—national Journal of Heat and Fluid Flow，2006，2（7）：135—143．

TE312

A

2095—4107（2013）05—0085—05

DOI 10．3969／j．issn．2095—4107．2013．05．012

2013—07—23；编辑：关开澄

国家重点基金项目（50934003）；教育部科技专项（FRF—MP—B 12006B）

王小锋（1985—），男，博士研究生，主要从事油藏数值模拟和渗流理论方面的研究．