索桁架组合体系的固有振动能量变分解

张文福，杜 娟，刘迎春，李 琛，任亚文

（1．东北石油大学防灾减灾工程及防护工程省高校重点实验室，黑龙江大庆 163318；2．东北石油大学土木建筑工程学院，黑龙江大庆 163318）

索桁架组合体系的固有振动能量变分解

张文福1，2，杜 娟1，2，刘迎春1，2，李 琛1，2，任亚文1，2

（1．东北石油大学防灾减灾工程及防护工程省高校重点实验室，黑龙江大庆 163318；2．东北石油大学土木建筑工程学院，黑龙江大庆 163318）

索桁架组合体系与普通梁板结构不同，需要考虑索力增量，振动特性较为复杂．首先，采用Timoshenko梁的连续化模型模拟桁架梁，推导桁架梁的等代抗弯刚度；采用能量变分法，分析索桁架组合体系固有振动，给出索桁架组合体系竖向振动频率解析解；分析770m跨度索桁架组合体系、900m跨度索桁架组合体系和1 200m跨度索桁架组合体系，与有限元ANSYS分析结果对比，误差在10%以内．该方法公式较简单、精度较高，可为索桁架组合体系的工程设计提供参考．

固有振动；能量变分法；索桁架组合体系；Timoshenko梁；有限元

0 引言

索桁架结构具有受力合理、施工方便、用料经济、造型简单、灵活、经济等优点，在大跨空间结构中得到迅速发展，随着跨度的不断增大，索桁架结构变得轻柔化，抗风成为首要问题．人们研究单索、双层索及劲性索，张文福、沈世钊等利用能量变分法原理，给出双层索在均布荷载、三角形荷载和对称三角形荷载作用下的挠度近似公式，并对单向劲性索结构进行固有振动分析，提出单向劲性索结构自振频率的计算公式；此外，还将双曲抛物面索网中的稳定索与承重索用劲性索代替，形成劲性索网结构，基于能量变分法和Rayleigh法提出劲性索网结构的自振频率和振型的简化计算公式［1—5］．Isabella Vassilopouloufe等建立多自由度的鞍形索网模型，并分析固有频率和振型［6］．Kassimali A等分析索网结构在对称荷载和非对称荷载作用下的非线性位移响应和刚度性能［7］．对于索和梁的组合结构，魏明海等利用Hamilton原理推导索—梁组合结构非线性动力学方程，同时考虑索的垂度及由梁和索之间模态耦合引起的非线性影响，利用Galerkin方法将索—梁组合结构非线性运动偏微分方程离散为一组常微分方程［8］．对于索桁架结构，李春光等以矮寨大桥为例，通过悬臂位移法反算得到主梁的等效刚度特性，设计桁式加劲梁悬索桥气弹模型，反映主跨结构的风振响应［9］．岳更新也以矮寨大桥为例，利用ANSYS有限元软件建立整体结构的三维分析模型并进行动力特性分析，给出横向、竖向、主缆、扭转及耦合振动的频率和振型［10］．白桦等以刘家峡大桥为例，研究采取导流板、中央稳定板、封闭防护栏等气动措施组合对钢桁架悬索桥颤振稳定性的影响［］．

鉴于对索桁架的固有振动研究较少，笔者采用能量变分法分析桁架的固有振动，推导索桁架的各阶竖向振动频率解析解，并利用ANSYS有限元软件对几种不同跨度的索桁架模型进行计算，对两种方法求得的结果进行比较，结果表明误差在10%以内．

1 等效力学模型

（1）在推导索梁结构计算理论时，采用假设［1—5］：①索是理想柔性的，既不受压，也不抗弯；②索是小垂度的，索的材料符合胡克定律；③索左右支座为固定铰支座，梁为简支梁；④连接索与梁的吊杆为刚性杆，不会发生轴向变形（见图1，其中L为索桁架长度）．

（2）当梁采用格构式构件时，为简化计算并进行连续化处理，建立桁架梁的连续化模型，采用假设：①梁的材料符合胡克定律；②沿梁长度方向的网格设置相当稠密，数目一般在5以上；③弯矩和轴力主要由上弦杆和下弦杆承担，剪力主要由斜腹杆承受；④梁以竖向振动为主，并且振动是微幅的．

桁架梁的剪切变形对刚度的影响较大，为了更好地模拟桁架梁的动力特性，采用双变量的Timoshen—ko梁［12］模型，即假设垂直于轴线的直线段变形后仍为直线，不再垂直于轴线，而是在平面内旋转一个角度θ，又与Euler梁理论不同，θ＝∂w／∂x，即产生一个剪切角γ＝∂w／∂x—θ（见图2），将此类桁架梁连续化为具有两个广义位移未知量的Timoshenko梁模型，其中w为位移，θ为转动角度，γ为剪切角．

图1 索桁架结构示意Fig．1 Schematic diagram of cable—truss structure

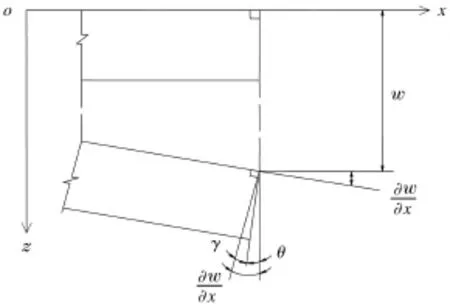
图2 桁架梁剪切角示意Fig．2 Shear angle schematic diagram

对于桁架梁（见图1），首先确定桁架梁的等代抗弯刚度［13—14］．在沿梁的长度方向任取一平面桁架单元（见图3（a）），假设等代实体梁单元的抗弯刚度为EIeq（见图3（b）），在一对弯矩M单独作用下，等代实体梁单元应变能Ubeam为

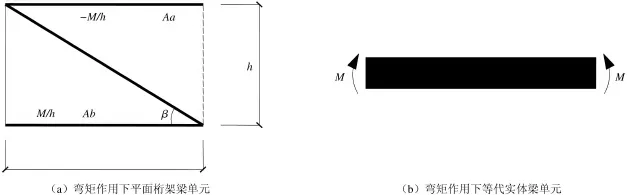
图3 在弯矩作用下的平面桁架与等代实体梁单元Fig．3 Element of plane truss and equivalent entities beam under moment

根据（2）中的假设③，弯矩主要由上、下弦杆承担，可得平面桁架梁单元应变能Utruss为

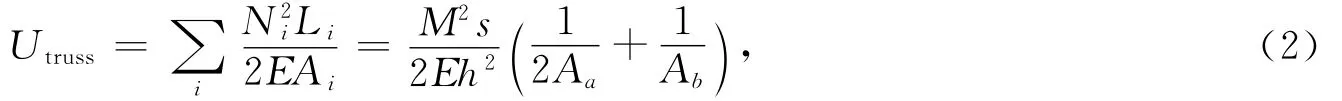
式（1—2）中：E为材料的弹性模量；Aa、Ab分别为上、下弦杆的截面面积；h、s分别为桁架梁的高度和节间距离．

根据等代实体梁单元应变能与平面桁架梁单元相等原则，可得桁架梁单元的等代抗弯刚度为

根据索曲线，确定索的几何伸长（假定跨度不变），在初始状态和振动状态下，索长度的表达式［1］分别为

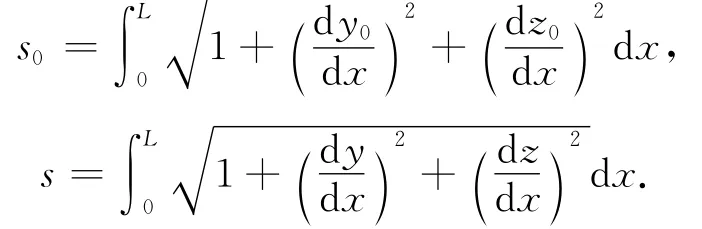
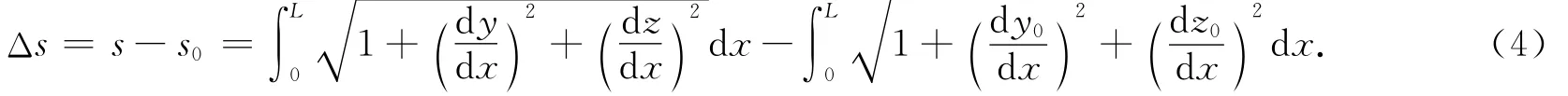
从初始状态到振动状态，整根索的总伸长度Δs的表达式为对于小垂度索，与1相比是小量，利用Taylor级数将式（4）根号项展开，若取前2项，则式（4）变为

2 固有振动分析

2．1 能量变分法

假设索桁架一起振动，并且只发生竖向振动，设索桁架的振动位移函数为

式（5—6）中：W（x）为振型函数，

索的状态曲线为

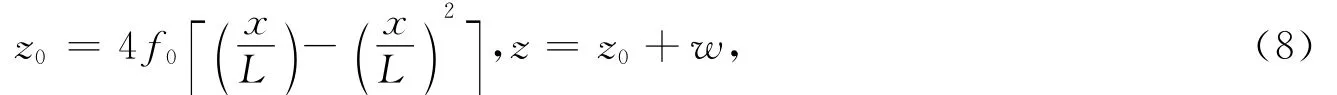
将式（8）代入式（5），索的总伸长度可简化为

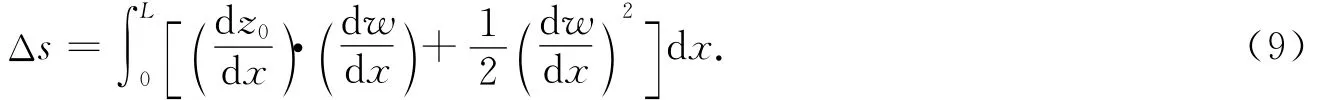
索的应变能为

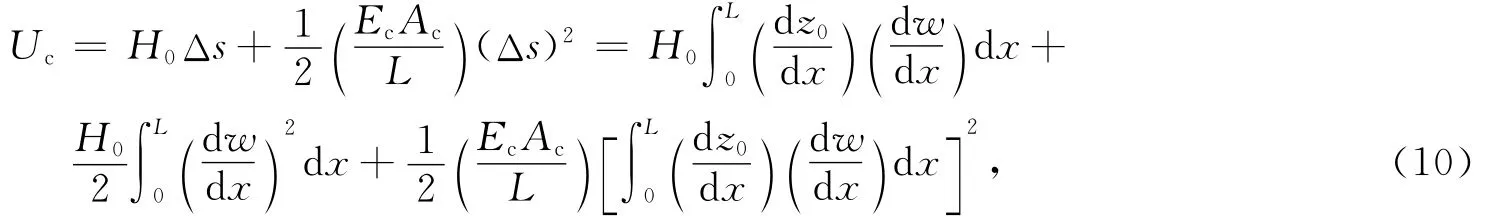
式中：H0Δs为索力增量产生的应变能；H0为索的水平拉力；EcAc为索的拉伸刚度．式（10）忽略后2项的影响．

索的荷载势能为桁架梁的应变能为

式中：EIeq为梁的竖向抗弯刚度．索桁架的总动能为

式中：¯m为索、桁架单位长度的总质量．索桁架结构的总能量方程为

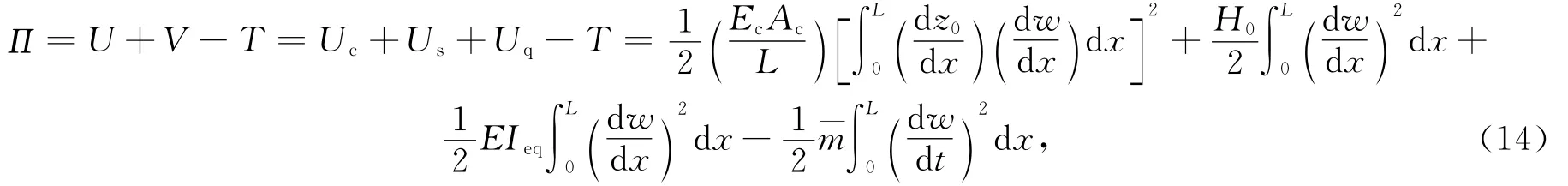
式中：U为结构总的应变能；V为结构总的荷载势能．

将式（6）代入式（14），根据瑞雷原理和势能驻值原理［15］∂∏／∂Am＝0，可得：

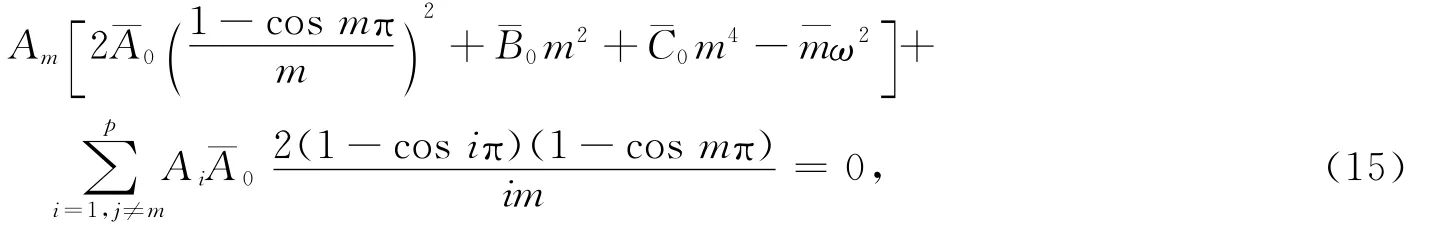
方程（15）的反对称振动展开式（m，i＝2，4，6，…p）为

求解式（16）可得反对称竖向振动频率为

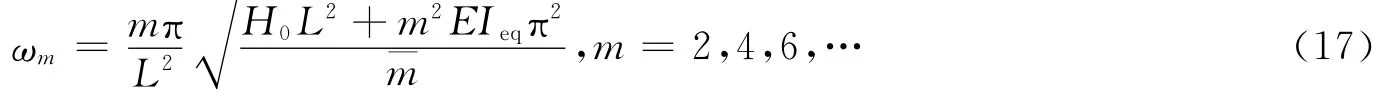
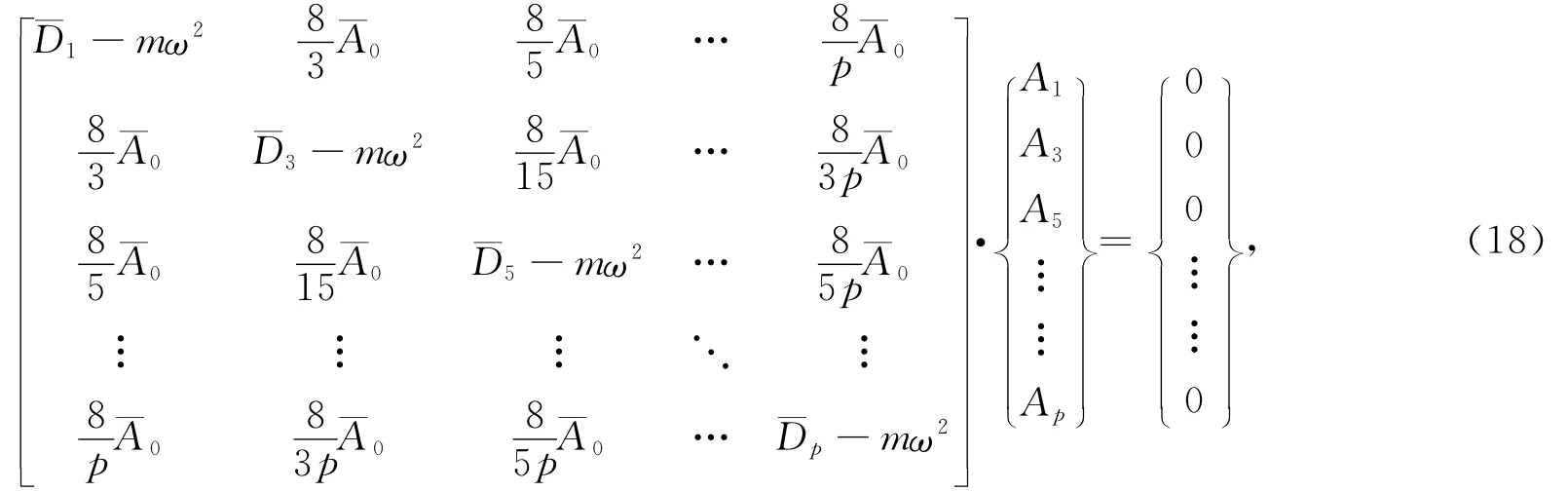
运用MATHEMATIC软件求解方程，得出各阶正对称振动频率；然后将各阶正对称频率代入式（18），得到系数矩阵；再将系数代入振型函数，求出各阶正对称振型．也可以采用手算方法求出各阶正对称振动频率．选取2个正弦函数组合，设振型函数表达式为

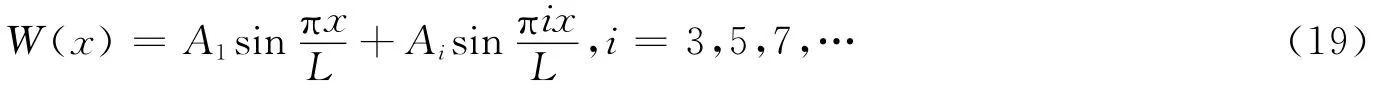
推导过程与式（8—18）类似，可得正对称振动简化的振动方程为

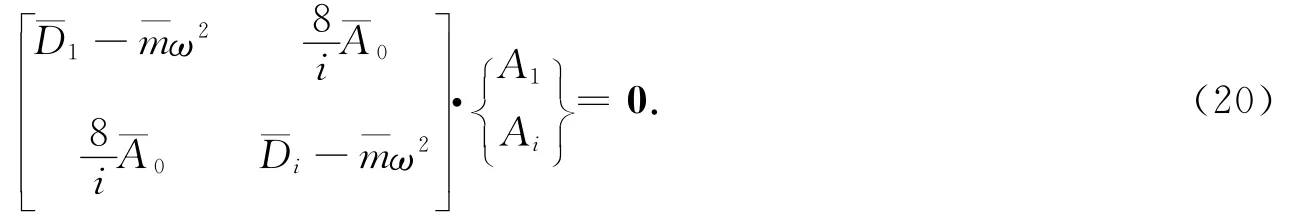
故频率方程为

解式（21）可得正对称竖向振动的频率为

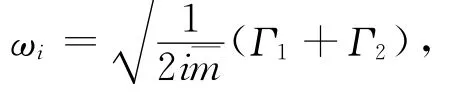
将ω1和ωi代入方程（20）可得系数A1和Ai，将A1和Ai代入振型函数式（19）可得正对称振动的各阶振型．

2．2 ANSYS有限元法

选取4种跨度索桁架模型进行有限元分析［16］，与能量变分法求得的理论解进行对比，模型参数见表1．跨度分别取770、900、1 200m．在有限元分析时，索和吊杆采用LINK10单元，桁架梁采用LINK180单元．

利用有限元法（FEM）和能量变分法分析770、900、1 200m跨度的索桁架，得到正对称竖向振动频率和反对称竖向振动频率（见表2和表3）．由表2和表3可以看出，对于前3阶频率，采用能量变分法分析得到的结果比采用有限元法分析得到的结果稍小；对于第四阶频率到第八阶频率，采用能量变分法分析得到的结果比采用有限元法分析得到的结果稍大，但是误差都在10%以内．

表1 索桁架结构的参数Table 1 The parameters of cable—truss structure

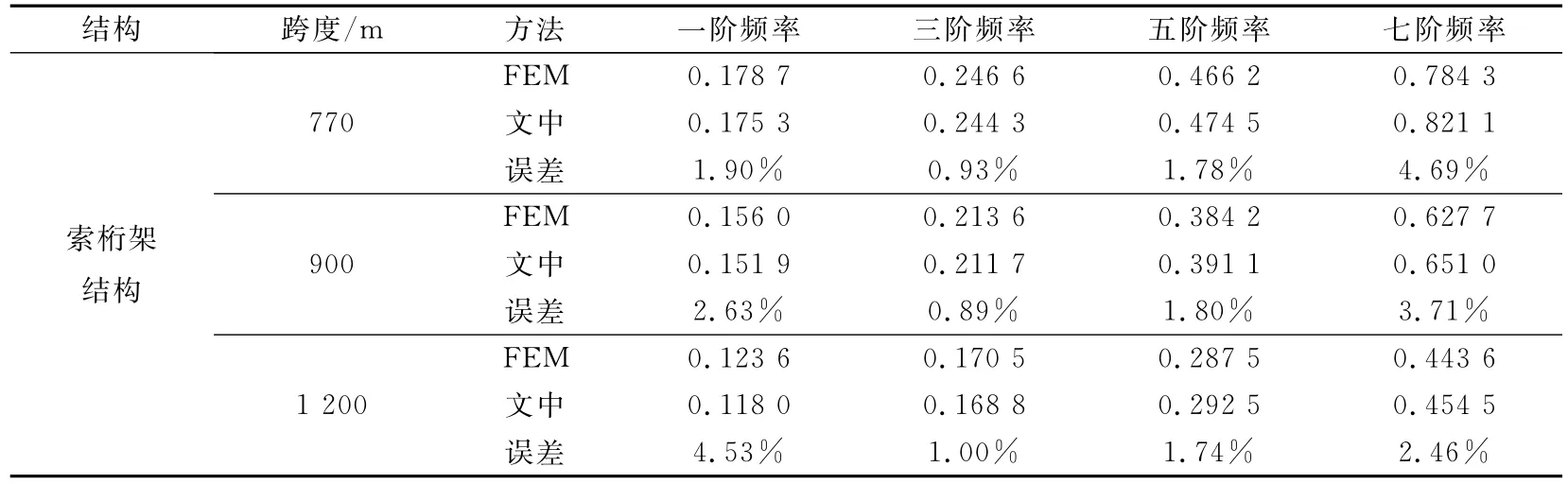
表2 索桁架结构的正对称竖向振动频率Table 2 The symmetric vertical vibration frequency of cable—truss structure Hz

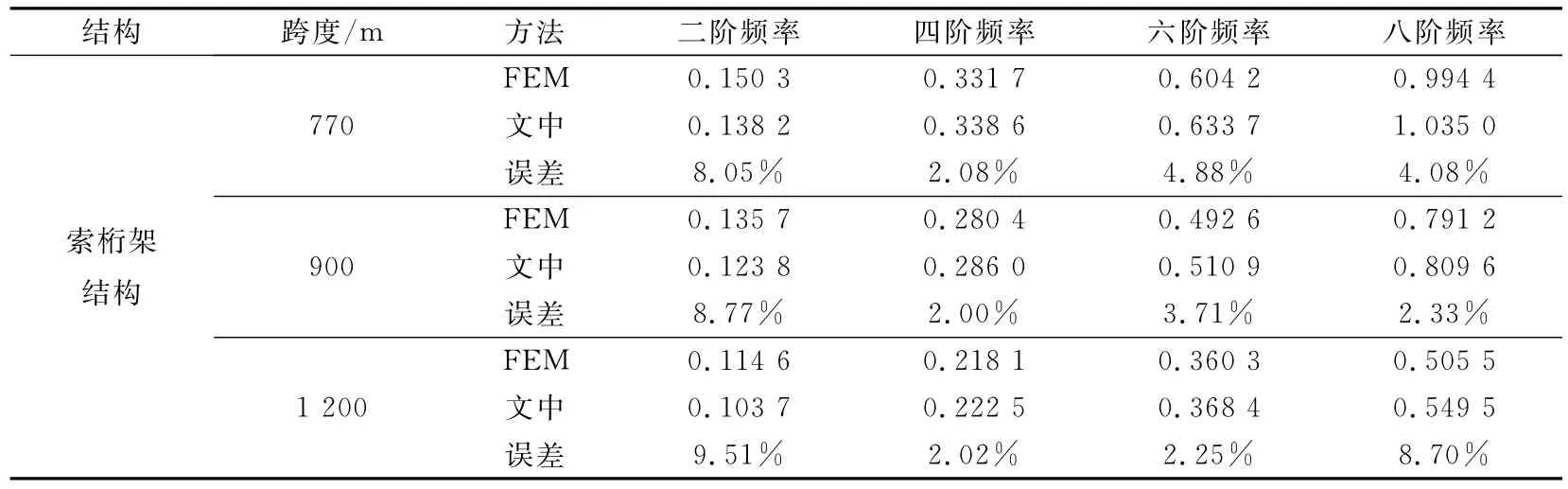
表3 索桁架结构的反对称竖向振动频率Table 3 Anti—symmetric vertical vibration frequency of cable—truss structure Hz

3 结论

（1）通过建立Timoshenko梁的连续化模型模拟桁架梁，推导桁架梁的等代抗弯刚度，基于能量变分法原理给出索桁架的竖向振动频率解析解．

（2）分析770m跨度索桁架、900m跨度索桁架和1 200m跨度索桁架，将竖向振动频率解析解与有限元分析得到的结果进行对比，结果误差在10%以内，说明能量变分法可以较好地分析索桁架的动力特性．

（3）文中给出的频率解析解实用、简洁、精度高，可供索桁架结构的抗风设计与抗震设计参考．

［1］ 张文福．空间结构［M］．北京：科学出版社，2005．Zhang Wenfu．Spatial structure［M］．Beijing：Science Press，2005．

［2］ 张文福，孙晓刚，张红星，等．预应力双层索静力分析的能量变分解［J］．空间结构，2007，13（1）：29—31．Zhang Wenfu，Sun Xiaogang，Zhang Hongxing，et al．The energy variational solutions for static analysis of prestressed double—layer cable［J］．Spatial Structures，2007，13（1）：29—31．

［3］ 张文福，孙晓刚．劲性索结构固有振动分析的能量变分法／／第六届全国现代结构工程学术研讨会论文集［C］．北京：工业建筑杂志社，2006：793—798．Zhang Wenfu，Sun Xiaogang．The energy variational solution for the nature vibration of stiff cable structure∥The Sixth National Con—ference on Structural Engineering［C］．Beijing：Industrial Construction Magazine，2006，793—798．

［4］ 张文福，刘文洋，巨秀丽．劲性索网结构的固有振动分析［J］．空间结构，2006，12（1）：55—58．Zhang Wenfu，Liu Wenyang，Ju Xiuli．Natural vibration analysis of stiff cable net structure［J］．Spatial Structures，2006，12（1）：55—58．

［5］ 沈世钊，徐崇宝，赵臣．悬索结构设计［M］．北京：中国建筑工业出版社，1997．Shen Shizhao，Xu Congbao，Zhao Chen．Design of suspension structure［M］．Beijing：China Building Industry Press，1997．

［6］ Isabella Vassilopoulou，Gantes C J．Vibration modes and natural frequencies of saddle form cable nets［J］．Computers ＆Structures，2010，88（1—2）：105—119．

［7］ Kassimali A，Parsi—Feraidoonian H．Nonlinear behavior of prestressed cable trusses［J］．Journal of Constructional Steel Research，1987，7（6）：435—450．

［8］ 魏明海，肖仪清．内外共振联合作用下索—梁组合结构非线性振动分析［J］．振动与冲击，2012，7（1）：79—84．Wen Minghai，Xiao Yiqing．Analysis of nonlinear vibration of beam combination structure of cable—the united action of internal and ex—ternal resonance［J］．Journal of Vibration and Shock，2012，7（1）：79—84．

［9］ 李春光，陈政清，张志田．大跨度桁式加劲梁悬索桥气弹模型等效设计［J］．振动与冲击，2009，28（9）：171—187．Li Chunguang，Chen Zhengqing，Zhang Zhitian．Equivalent design of aeroelastic model for a long—span suspension bridge with truss stiffening girder［J］．Journal of Vibration and Shock，2009，28（9）：171—187．

［10］ 岳更新．桁式加劲梁悬索桥抗风动力特性分析［J］．萍乡高等专科学校学报，2008（6）：24—28．Yue Gengxin．Analysis on resisting wind dynamic characteristics on suspension bridge with truss beam［J］．Journal of Pingxiang Col—lege，2008（6）：24—28．

［11］ 白桦，李宇，李加武，等．钢桁架悬索桥颤振稳定性能研究［J］．振动与冲击，2013，32（4）：90—95．Bai Hua，Li Yu，Li Jiawu，et al．Flutter stability of a steel truss girder suspension bridge［J］．Journal of Vibration and Shock，2013，32（4）：90—95．

［12］ Ji Yao Shen，Jen—Kuang Huang，Taylor L W．Timoshenko beam modeling for parameter estimation of NASA mini—mast truss［J］．Journal of Vibration and Acoustics，1993（115）：21—24．

［13］ 张文福，赵文艳．网架结构的数值模拟分析与设计［M］．哈尔滨：哈尔滨地图出版社，2003．Zhang Wenfu，Zhao Wenyan．Numerical simulation analysis and design of the grid structure［M］．Harbin：Harbin map Press，2003．

［14］ 张文福，张百龙．网架结构设计［M］．哈尔滨：哈尔滨工业大学出版社，1994．Zhang Wenfu，Zhang Bailong．Design of double—layer space grids［M］．Harbin：Harbin Institude of Technology Press，1994．

［15］ 胡海昌．弹性力学的变分原理及其应用［M］．北京：科学出版社，1981．Hu Haichang．Variational principles in elasticity and its applications［M］．Beijing：Science Press，1981．

［16］ 刘涛，杨凤鹏．精通ANSYS［M］．北京：清华大学出版社，2002．Liu Tao，Yang Fengpeng．Proficient in ansys［M］．Beijing：Tsinghua University Press，2002．

TU311

A

2095—4107（2013）05—0103—06

DOI 10．3969／j．issn．2095—4107．2013．05．015

2013—05—13；编辑：任志平

国家自然科学基金项目（51178087）；黑龙江省教育厅重点项目（12511z004）

张文福（1965—），男，博士，教授，主要从事结构工程、抗风与抗震方面的研究．

方程（15）的正对称振动展开式（m，i＝1，3，5，…p）：