一类N-策略M/G/1排队系统队长分布

刘晓燕，孙玺菁，刘 丹

（海军航空工程学院系统科学与数学研究所，山东烟台264001）

自从YADIN 和NAOR[1]引入了N-策略以来，具有N-策略控制机制的排队系统理论已取得了丰硕的成果[2-9]。排队系统队长的稳态概率分布在系统容量设计中有着重要的应用价值，而直接来求队长的稳态分布是非常困难的。基于此，本文研究带启动/关闭时间的N-策略M/G/1排队系统，提出了一种简便有效的算法来推导稳态队长概率分布的解析结果。

1 模型描述

本文研究的带启动/关闭时间的N-策略M/G/1 排队系统模型描述如下：

1）顾客到达形成参数为λ的Poisson 流，且根据到达顺序排成一队列并实行先到先服务机制，服务台一次只能服务一个顾客；

2）系统只有一个服务台，服务时间（记作G）是独立同分布的随机变量且具有一般分布函数G(t)(t≥0)；

3）系统实行带启动/关闭时间的N-策略休假机制：每当系统变空时，服务台不是立即关闭，而是进行一段随机时间D的“关闭准备时间”后再关闭；如果没有顾客在“关闭准备时间”内到达，服务员就马上进行休假，直到系统中累计有N个顾客时又开始启动服务台进行服务，且服务台要进行一段随机时间U的“启动准备时间”才能开始工作，直至系统再次变空；

4）如果有顾客在“关闭准备时间”D内到达，那么，服务台立即停止关闭准备且不需要重新启动，立即为顾客服务，直到系统再次变空而重新做关闭准备；

5）顾客到达过程、服务台服务过程、“关闭准备时间”及“启动准备时间”是彼此独立的；

6）在t=0时刻，如果系统是空的，则到达的第一个顾客立即被服务。即只有在服务台繁忙一段时间后系统才实行带启动/关闭时间的N-策略休假机制，所得平稳结果与此假设无关。

2 M/G/1排队系统队长的基本公式

在对本文模型进行分析前，先引入经典M/G/1 排队系统的部分相关结果。首先，定义一些基本概念。忙期：从服务员开始为顾客服务的时刻起，直到系统再次变空为止这一段时间；闲期：从系统变空的时刻起，直到服务员再次开始为顾客服务为止这一段时间。令(j=0,1,2,…)表示平稳状态下队长的概率分布，则[2]：

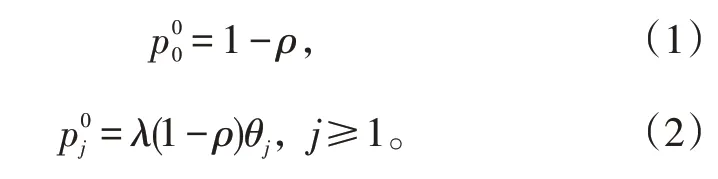
式（2）中：

g(λ)=当j≤0时，规定表示忙期中系统稳态队长分布，ρ=λE[G]为交通强度。M/G/1排队系统队长的概率母函数为

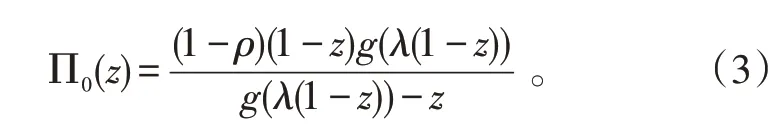
3 模型分析

1）系统队长的概率母函数。本文所研究的模型可看做是第2部分中经典M/G/1排队系统的一种推广形式，模型中忙期的开始方式可归纳成以下情形。

情形1：在服务台“关闭准备时间”内没有顾客到达，其概率为D∗(λ)。在这种情形下，服务员就马上进行休假，直到系统中累计有N个顾客时，又开始启动服务台进行服务。忙期初始时，系统队长的概率母函数为zNU∗(λ-λz)，其中U∗(s)是U的LS变换。

情形2：在服务台“关闭准备时间”内有顾客到达，其概率为1-D∗(λ)。在这种情形下，服务台立即停止关闭准备且不需要重新启动，立即为顾客服务，此时开始的忙期初始时刻系统中只有1名顾客。

由已知随机分解结果[3]，忙期初始时，系统队长分布的概率母函数为

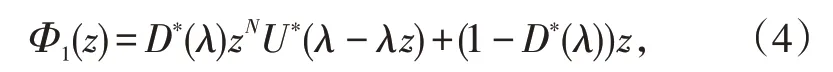
式中，U∗(λ-λz)表示“启动准备时间”内到达的顾客数的概率母函数。

由MEDHI和TEMPLETON推导出的结论[4]，带启动/关闭时间的N-策略M/G/1 排队系统中队长分布的概率母函数的随机分解式仍然存在：式（5）中为闲期内期望到达的顾客数。

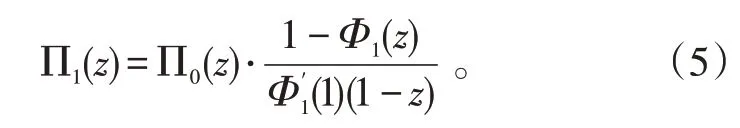
2）系统队长分布。首先，由系统附加队长的概率母函数得到系统附加队长分布。通过式（5）可以看出稳态队长分布可以看作是2 个随机变量之和，其一是一般M/G/1排队系统队长，其二是由带启动/关闭时间的N-策略休假机制所引起的附加队长分布。系统附加队长的概率母函数为

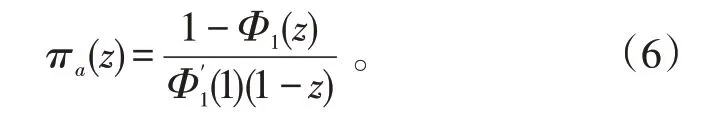
由概率母函数定义，系统附加队长概率分布为：

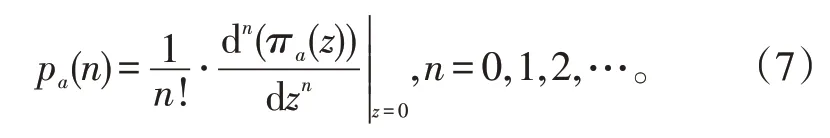
基于此，当i＜N时，有：

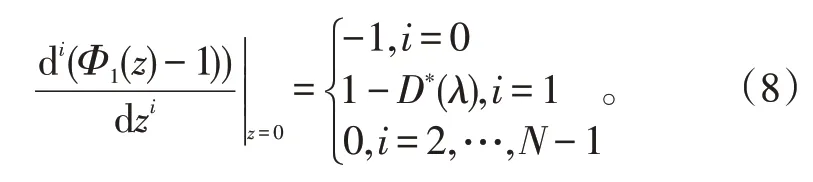
当i≥N时，有：

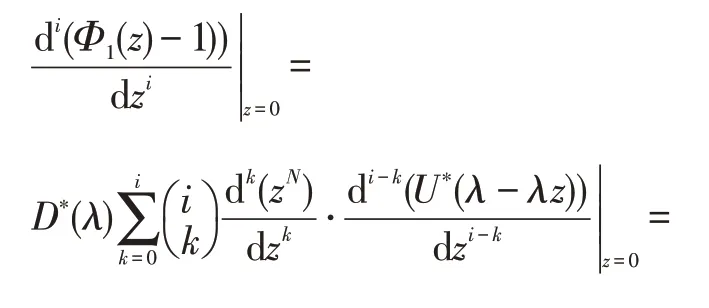
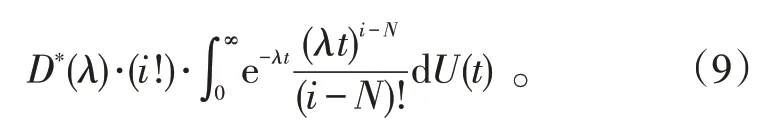
将式（8）及式（9）代入至式（7）中，可得系统附加队长分布：

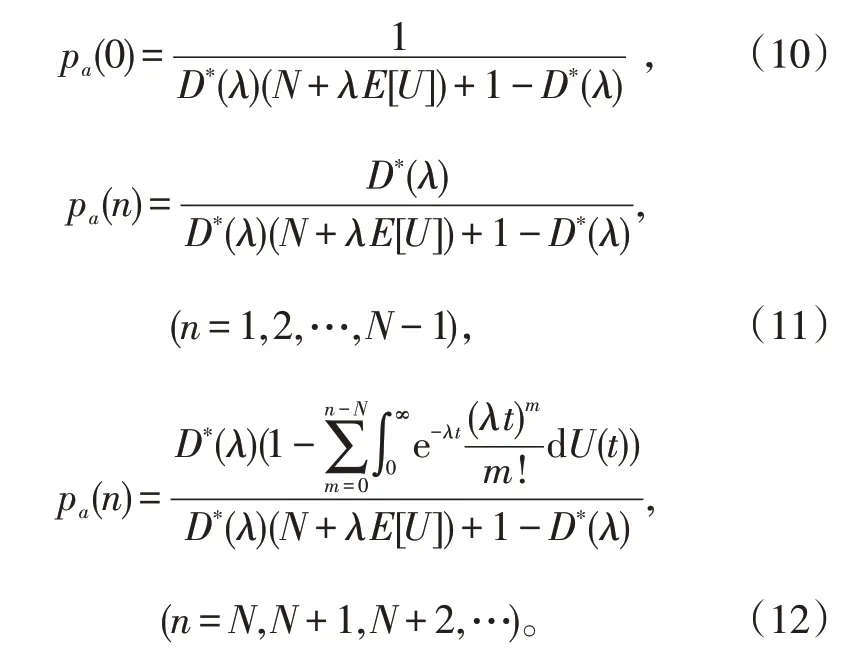
接下来，再研究系统队长分布。显然，由链式法则，系统中有0名顾客（n=0）的概率为

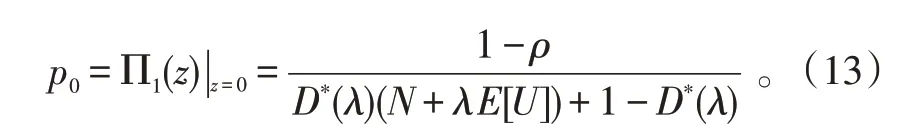
当n=1,2,…,N-1时，由Leibniz 公式，通过式（5）可得系统中有n名顾客的概率为

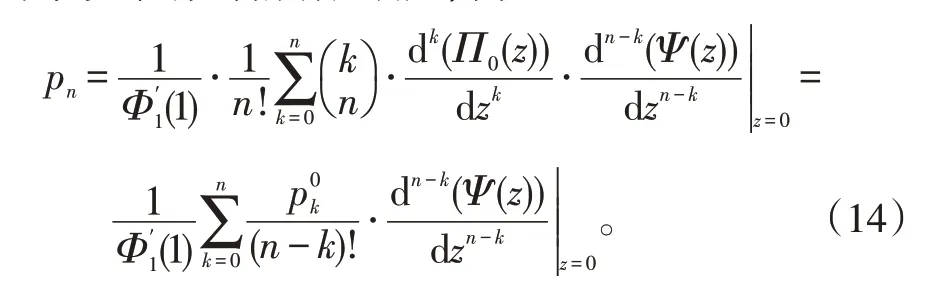
式（14）中，p0k由式（1）、（2）给出。令，再次利用链式法则的推导过程，若n-k＜N，有

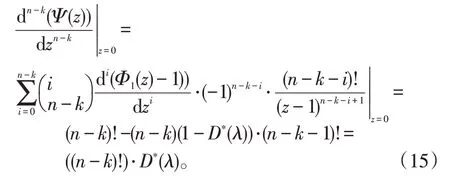
将式（15）代入式（14）并结合式（2），可得系统队长分布：

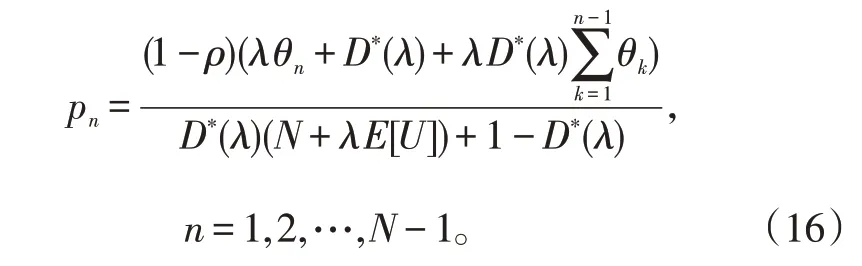
当n≥N时，我们讨论以下情形。

若n-k≥N，即k≤n-N，有：

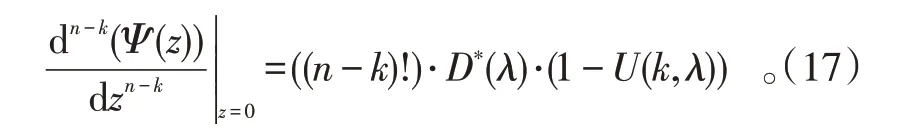
由式（15）及式（17）并结合式（2），可得系统队长分布：

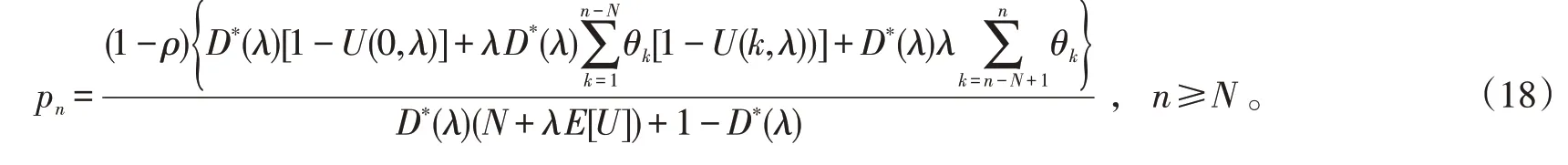
系统队长分布表达式由式（13）、（16）及（18）给出，这些公式可以用于计算平稳状态下队长的概率分布。

注：若本文所研究的系统中“启动准备时间”为0，即E[U]=0、U(0,λ)=1、U(k,λ)=1，此时系统简化为具有延迟关闭时间的N-策略M/G/1排队系统，简化结论与文献[2]中的结论一致，而本文所用方法较文献[2]中全概率分解法简便很多。

4 数值实验

下面借助数值计算技术进一步考察稳态队长分布的表达式。假设服务时间服从负指数分布且E[G]=1/μ，启动时间服从3 阶Erlang 分布且E[U]=3/β，关闭时间服从4 阶Erlang分布且E[D]=4/γ，当λ=1、μ=2、γ=2、N=5时，结果如表1所示。

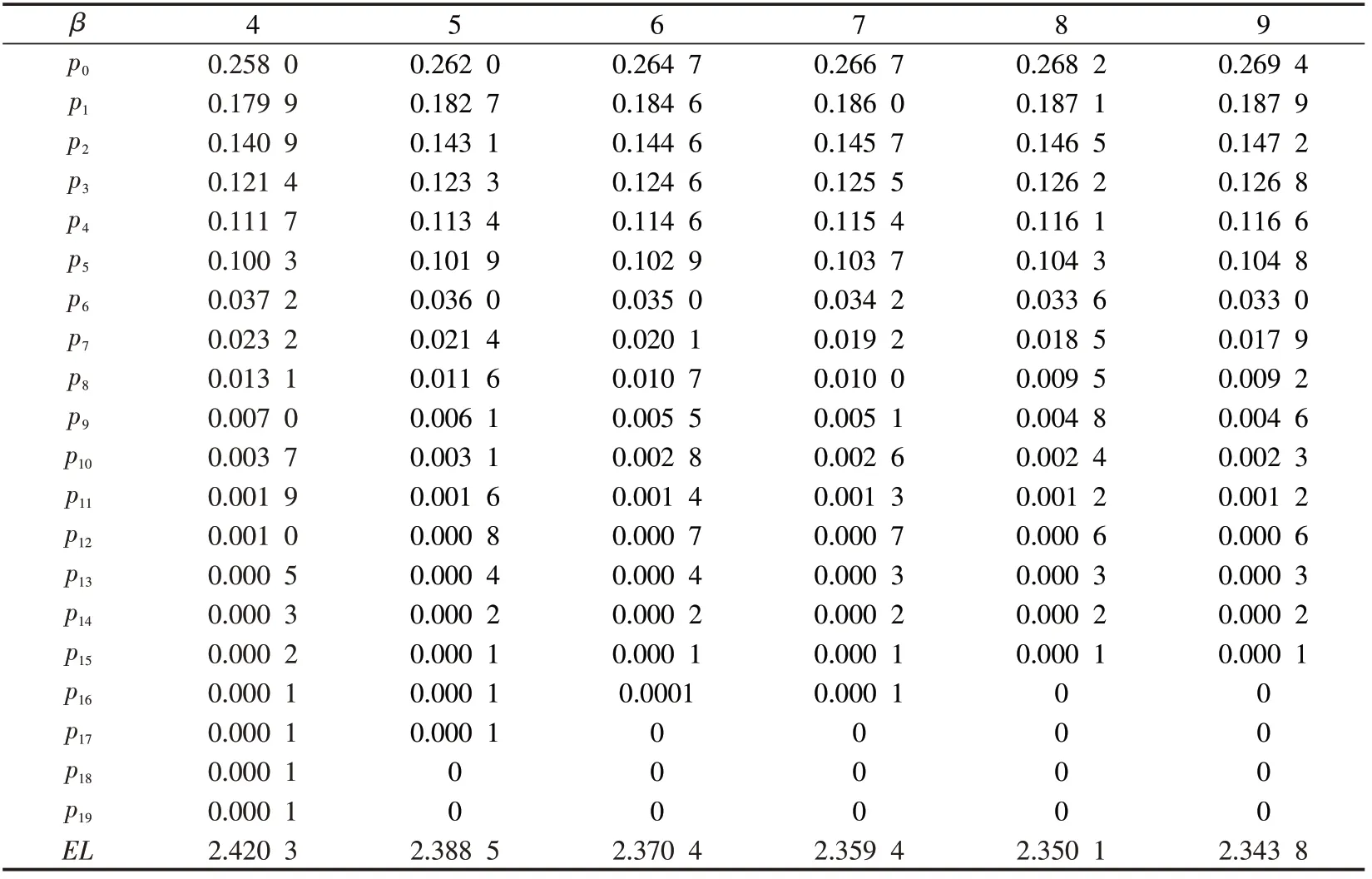
表1 队长分布

通过表1 可以看出，随着β的增大，在其他参数固定的情况下，①系统变空的概率随之增大；②系统队长为n(n=1,2,…,N)的概率随之增大；③系统队长为n(n=N+1,N+2,…)的概率随之减小。平均队长（EL）随着β的增大而减小。值得注意的是，实际中的排队系统容量往往是有限的，工程设计中需要综合考虑平均队长和稳态队长分布，而仅仅以平均队长作为依据，可能导致系统容量设计偏小。

[1] YADIN M，NAOR P.Queueing systems with a removable service station[J]. Operational Research Quarterly，1963，14（4）：393-405.

[2] 唐应辉.延迟N-策略M/G/1 排队系统队长的瞬态和稳态分布[J]. 系统工程理论与实践，2007，27（11）：132-136.

TANG YINGHUI. The transient and equilibrium distributions of the queue-length for M/G/1 queue with delayed N-Policy[J]. Systems Engineering-Theory & Practice，2007，27（11）：132-136.（in Chinese）

[3] FUHRMANN S W，COOPER R B.Stochastic decompositions in the M/G/1 queue with generalized vacations[J].Operations Research，1985，33（5）：1117-1129.

[4] MEDHI J，TEMPLETON J G C. A poisson input queue under N-policy and with a general start up time[J]. Computers and Operations Research，1992，19（1）：35-41.

[5] 唐应辉，刘燕.N-策略M/G/1 排队系统队长分布表达式[J].运筹与管理，2006，15（3）：40-50.

TANG YINGHUI，LIU YAN. The expression of the queue length distribution for M/G/1/∞queue with N-policy[J]. Operations Research and Management Science，2006，15（3）：44-50.（in Chinese）

[6] 冯建英，吴云江.带关闭期的随机N-策略的M/G/1排队系统[J].工程数学学报，2009，26（3）：90-98.

FENG JIANYING，WU YUNJIANG. The M/G/1 queue under vacation policies with closedown time and the random N-policy[J]. Chinese Journal of Engineering Mathematics，2009，26（3）：90-98.（in Chinese）

[7] 罗海军，朱翼隽.带有负顾客的N 策略工作休假M/M/1排队[J].运筹与管理，2010，19（1）：104-109.LUO HAIJUN，ZHU YIJUAN.The M/M/1 working vacation queue with negative customers and N-policy[J]. Operations Research and Management Science，2010，19（1）：104-109.（in Chinese）

[8] 唐应辉，蒲会，余玅妙.带启动时间的N-策略M/G/1 排队系统的队长[J].系统工程理论与实践，2011，31（1）：131-137.

TANG YINGHUI，PU HUI，YU MIAOMIAO. Queue size of M/G/1 queueing system with N-policy and set-up times[J]. Systems Engineering-Theory & Practice，2011，31（1）：131-137.（in Chinese）

[9] 刘名武，马永开.启动延迟N-策略批到达多重休假排队[J].数学的实践与认识，2011，41（13）：137-144.

LIU MINGWU，MA YONGKAI. Batch-arrival queue with multiple vacations and delayed setup times under Npolicy[J]. Mathematics in Practice and Theory，2011，41（13）：137-144.（in Chinese）