左截断数据下回归函数的变窗宽局部线性M估计

杨益民

（杭州师范大学理学院，浙江杭州310036）

0 引 言

设｛（Xi，Yi），1≤i≤N｝是来自（X，Y）的R×R随机向量．在非参数统计中，回归函数m（x）＝E（Y｜X＝x）常用来描述反应变量Y和协变量X之间的关系．多年来，已经有很多方法用来估计m（x）．Fan和Jiang［1］构造了m（x）及其导数的局部线性M估计，即找到a和b使得下面式子达到最小：

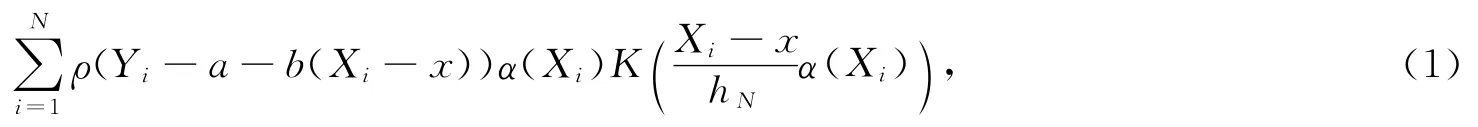
这里α（·）为非负函数，ρ（·）为抗异常值函数，0＜hN→0为窗宽（N→∞），K（·）为核函数．

以下简单地叙述左截断数据．设｛（Xk，Yk，Tk），k≥1｝来自总体（X，Y，T）的一列随机向量，这里T为截断变量．假设T和（X，Y）是相互独立的，并且T有连续的分布函数G．在左截断模型中，对i＝1，…，N，生存时间Yi被截断变量Ti干扰，当Yi≥Ti时，Yi和Ti都能观察到，而当Yi＜Ti时，Yi和Ti都不能观察到．由于截断的发生，N是未知的，n是实际观察到的样本容量，并且是随机的，显然有n≤N．为了避免引起混淆，记（X1，Y1，T1），…，（Xn，Yn，Tn）为实际观察到的样本．设为随机变量Y能观察到的概率．由于θ＝0意味着什么数据都观察不到，所以本文通篇假设θ＞0．由于N未知，而n已知（尽管随机的），因此规定下文的结果陈述如下：概率测度是关于样本容量N的，而条件概率P是关于观察的样本容量n的．另外和E分别为在和P下的期望．

对任意分布函数L，记aL:＝inf｛x:L（x）＞0｝和bL:＝sup｛x:L（x）＜1｝，U（x）表示点x的某个邻域．设F（·）为Y的分布函数，F（·，·）和f（·，·）分别为（X，Y）的联合分布函数和联合概率密度，则（X，Y）的条件分布函数为

由上式可以得到（X，Y）的条件密度函数为

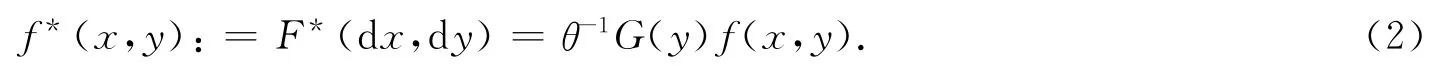
定义C（y）＝P（T≤y≤Y｜Y≤T）＝θ－1G（y）［1－F（y）］，考虑它的经验分布函数Cn（y）＝I（Ti≤y≤Yi）．沿用Lynden－Bell［2］的思想，F（·）和G（·）的最大似然估计分别为

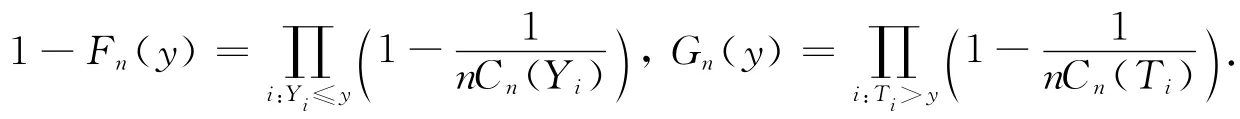
左截断数据下，由于观察样本为｛（Xi，Yi，Ti），1≤i≤n｝，因此式（1）不能直接用．Ould－Saïd和Lemdani［3］对左截断数据下构造了m（·）的NW估计如下：

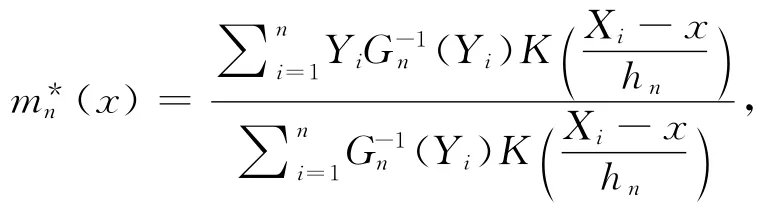
这里K（·）定义在R上的核函数，0＜hn→0为窗宽（n→∞）．更一般地，NW估计可以看作下列优化问题的解：

基于式（1）和（3），构造变窗宽下的局部线性M估计（LLME），即寻找和使得下列式子达到最小：

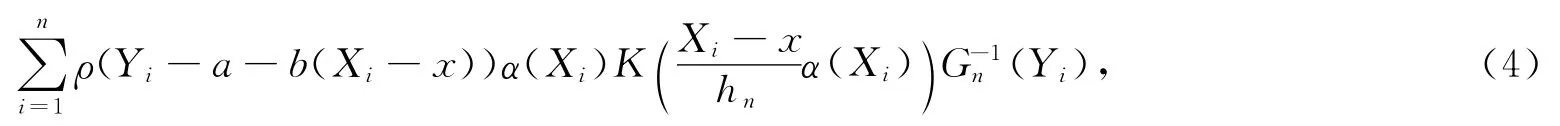
或满足下面等式

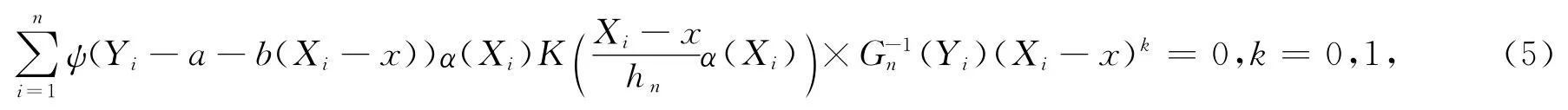
这里ψ（·）为ρ（·）的导函数．

1 主要结果

设ε＝Y－m（X），r0＝（m（x0），hnm（x0））T，μj＝

在给出结果之前，需要先给出下面的条件：

（A0）aG＜aF，bG＜bF．

（A1）K（·）为连续的概率密度函数，且紧支撑，不妨设［－1，1］．

（A2）α＊≡minxα（x）＞0和α（·）在点x0上连续．

（A3）回归函数m（·）在点x0上具有连续的二阶导数．

（A4）窗宽hn满足hn→0和nhn→＋∞．

（A5）对x∈U（x0），＝0．

（A6）X的密度函数fX（x）在点x0上连续，且fX（x0）＞0．

（A7）函数ψ（·）是连续的，且几乎处处具有导数ψ′（·）．进一步，满足

（i）函数Λ1（x）＝和Λ2（x）＝在点x0上为正的且连续．

（ii）存在γ＞0满足和在x∈U（x0）上有界．（A8）函数ψ′（·）满足当δ→0时，和ψ（ε）－ψ′（ε）z｜｜X＝x］＝o（δ）在x∈U（x0）上一致成立．

注1 （A0）中的条件aG＜aF确保G（Y）≥G（aF）＞0，这样使得Gn（Yi）≠0，因此本文的估计是有意义的．条件（A1）～（A8）由Fan和Jiang［1］提出，后为很多作者［4－5］引用．

定理1 在条件（A0）～（A8）下，等式（5）存在解，记为，使得∞，这里．

定理2 假设条件（A0）～（A8）成立，则

推论1 在定理2条件下，有

接下来，给出定理2的一个特殊情形，下面这个推论实际上是文［1］中的定理2．2．

推论2 在定理2的条件下，如果θ→1，有

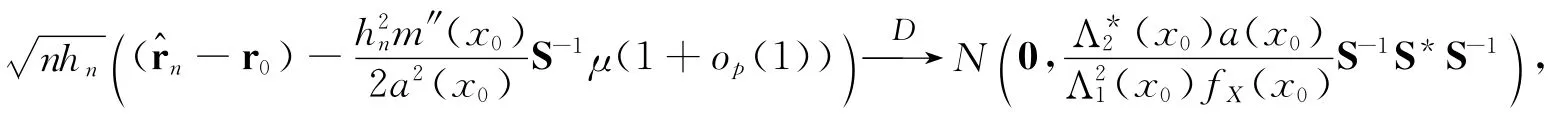
2 模拟研究

下文通过模拟研究回归函数m（x）的局部线性M估计在有限样本下的效果．特别地，通过整体均方误差比较和NW估计的效果．考虑下面模型：

这里Xi～Uniform（－2，2）独立于εi，εi下面确定．该模型用于文［1］中．本文模拟N个独立同分布的随机变量Ti～N（μ，1），这里μ可以调整来获得θ．接受满足Yi≥Ti的样本（Xi，Yi，Ti），i＝1，…，n．在这个例子中，使用Epanechnikov核函数，并且选择Huber型函数ψ（y）＝max｛c，min｛y，c｝｝．为了比较和，考虑εi下面不同的分布：

（a）标准正态分布：εi～N（0，1）；

（b）受污染的正态分布：εi～0．85N（0，1）＋0．15N（0，82）；

（c）柯西分布：εi～C（0，1）．

由模型（6）分别产生容量n为200，500和800的样本．在表1中，取θ值分别为30%，60%，90%，并且基于M＝200次重复计算这些估计的整体均方误差（GMSE）．另外，利用一个简单方法选择窗宽，对窗宽hn的取值从0．05到1，增量为0．1，选择一个使得GMSE达到最小的窗宽．GMSE定义如下：

从表1看出：1）当误差服从标准正态分布时，这两个估计模拟的效果都比较好．但是当误差为受污染的正态分布以及柯西分布时，更稳健；2）这两个估计模拟的效果随着n越大而越好；3）这两个估计的效果会受到θ的影响，且随着θ越大而越好．

表1 估计和的整体均方误差Tab．1 The global mean squared errors of the estimatorsand

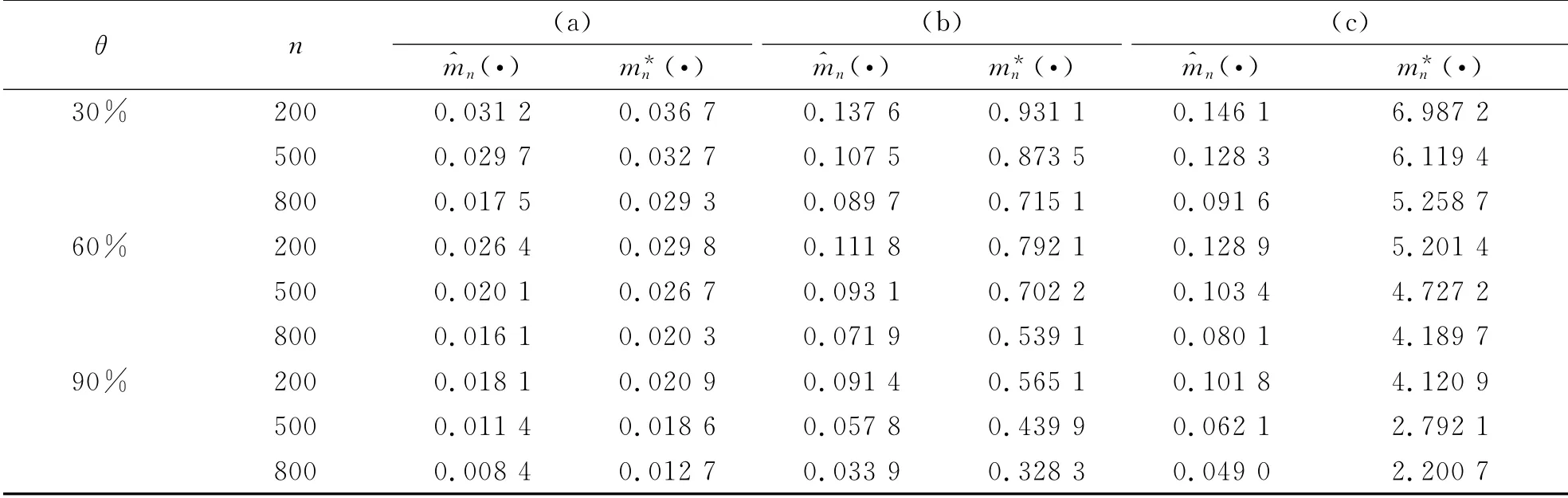
表1 估计和的整体均方误差Tab．1 The global mean squared errors of the estimatorsand

θ n （a）＾mn（·）m＊n（·）（b）＾mn（·）m＊n（·）（c）＾mn（·）m＊n（·）30%200 0．031 2 0．036 7 0．137 6 0．931 1 0．146 1 6．987 2 500 0．029 7 0．032 7 0．107 5 0．873 5 0．128 3 6．119 4 800 0．017 5 0．029 3 0．089 7 0．715 1 0．091 6 5．258 7 60%200 0．026 4 0．029 8 0．111 8 0．792 1 0．128 9 5．201 4 500 0．020 1 0．026 7 0．093 1 0．702 2 0．103 4 4．727 2 800 0．016 1 0．020 3 0．071 9 0．539 1 0．080 1 4．189 7 90%200 0．018 1 0．020 9 0．091 4 0．565 1 0．101 8 4．120 9 500 0．011 4 0．018 6 0．057 8 0．439 9 0．062 1 2．792 1 800 0．008 4 0．012 7 0．033 9 0．328 3 0．049 0 2．200 7

3 定理的证明

引理1 假设条件（A0）～（A8）成立．对任意随机变量序列，满足max1≤i≤n｜ηi｜＝op（1），

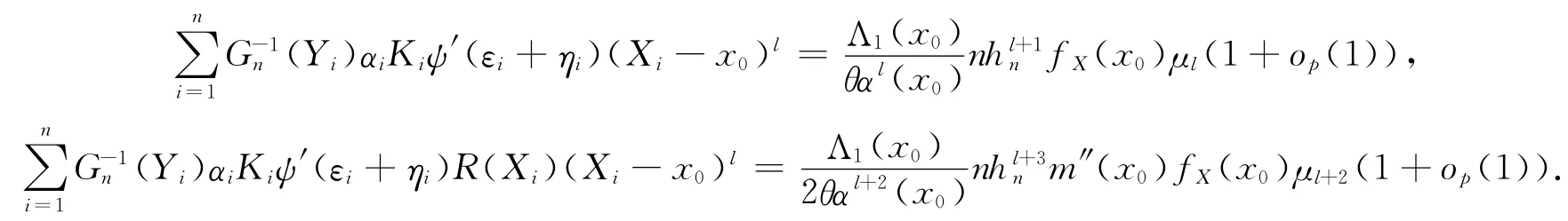
证明 以下仅证明第一个等式，第二个等式可以类似地证明．注意到

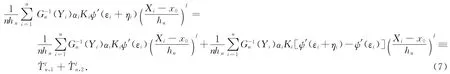
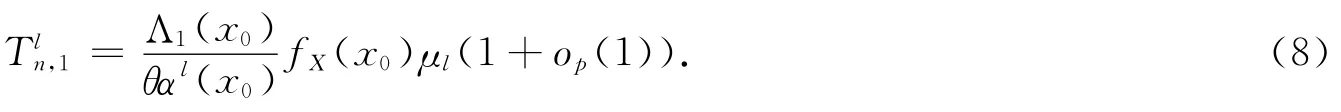
通过条件（A1），（A6），（A7（i））和式（2），有

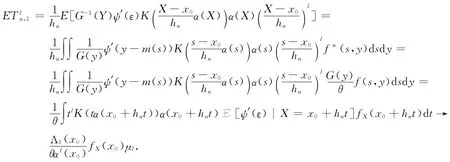
由条件（A1），（A6），（A7（ii））和式（2），得

结合式（8），有

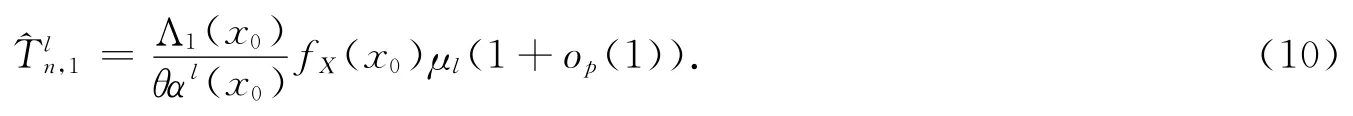
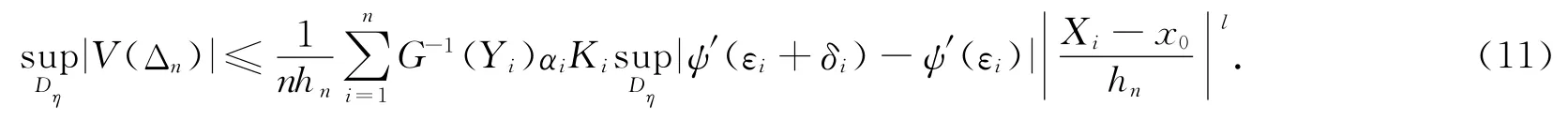
注意到｜Xj－x0｜≤hn／α＊，由（A8）和式（11）得

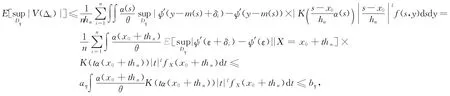
这里aη和bη为两个正数列，当η→0时都趋近于0．由于max1≤i≤n｜ηi｜＝op（1），这样＝op（1），这里．通过，得到＝op（1），结合式（7）和（10），引理1得证．

引理2 在条件（A0）～（A8）下，有

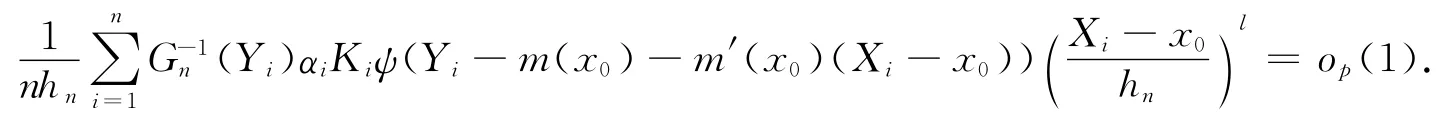
证明 由Yi＝m（Xi）＋εi，R（Xi）＝m（Xi）－m（x0）－m′（x0）（Xi－x0），得

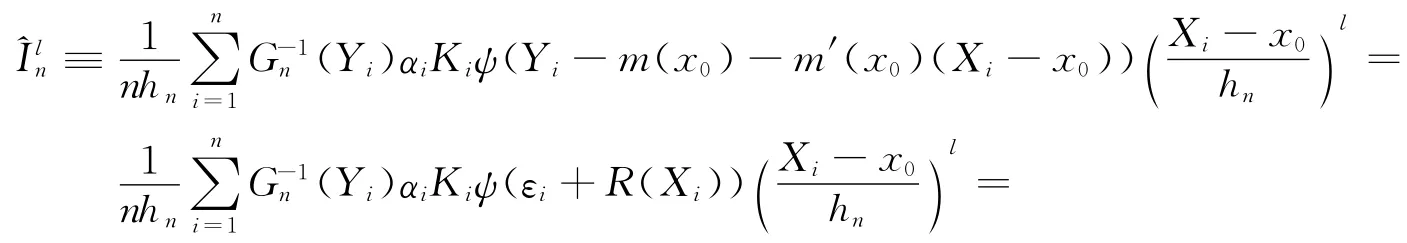
通过（A3）和泰勒展开式，对｜Xi－x0｜≤hn／α＊（i＝1，…，n），有

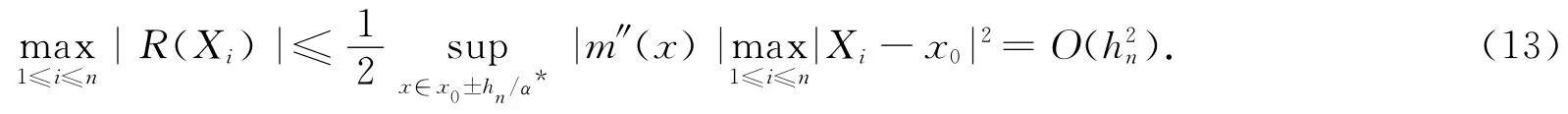
通过（A8）和式（13），类似引理1的证明，得到

应用引理1的第二个结论，有

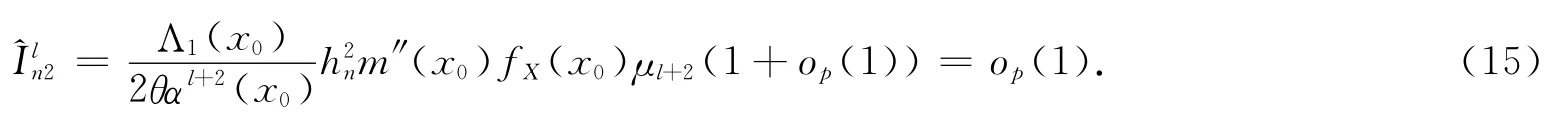
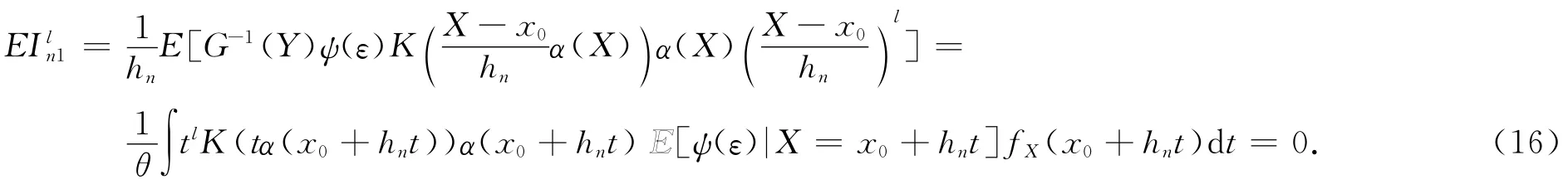
另一方面，由条件（A1），（A6），（A7（i））和式（2）得

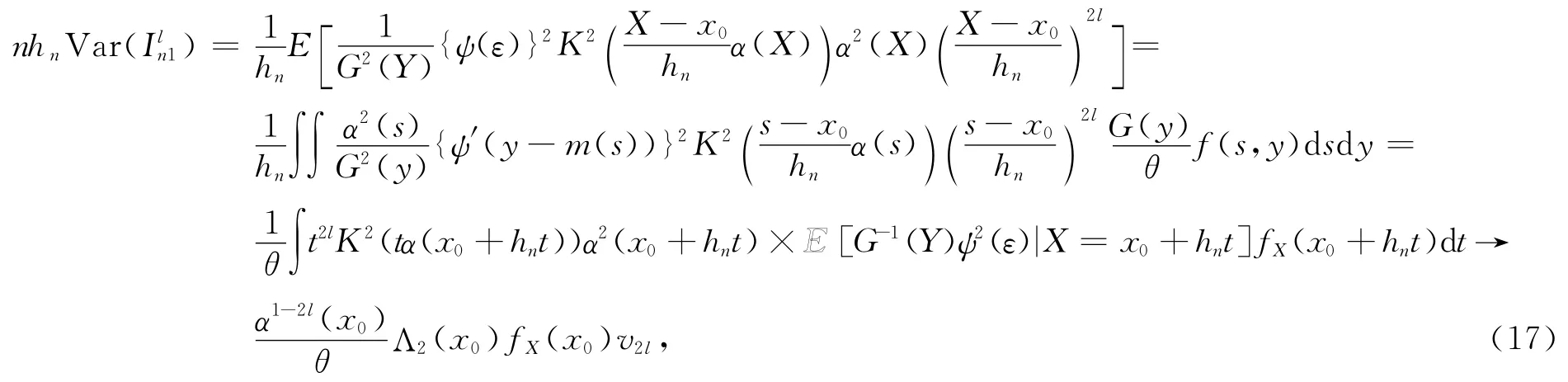
引理3 在条件（A0）～（A8）下，有

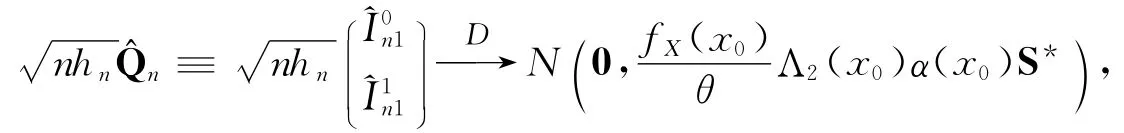
为了证明这结果，仅仅证明，对任意给定的实数向量d＝（d1，d2）T≠0，有，θ－1Λ2（x0）fX（x0）α（x0）dTS＊d）．而

通过式（16）得EWi＝0．类似式（17）的证明，有

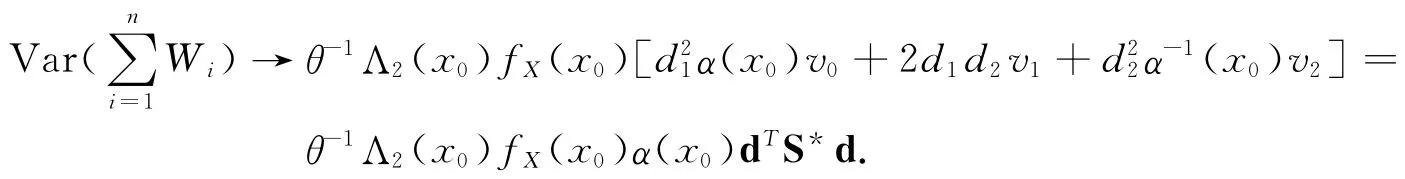
由（A7（ii）），得到

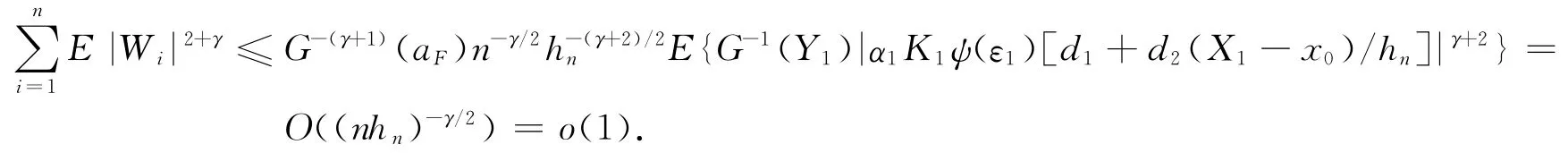
这样，利用Lyapunov中心极限定理，有

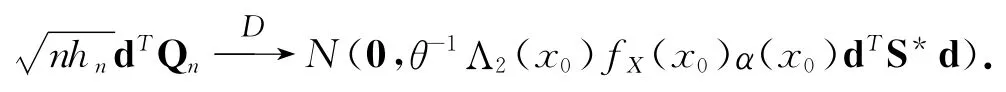
注意到

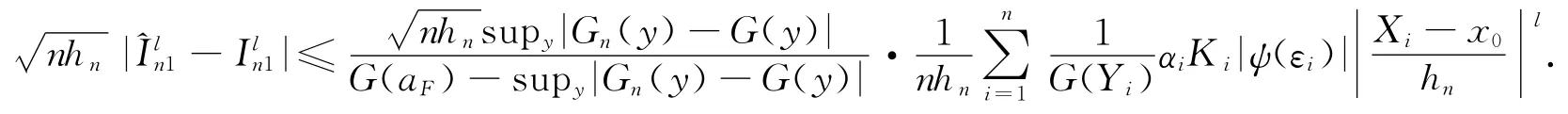
定理1的证明 设r＝（a，hnb）T和＝（1，（Xi－x0）／hn）T．注意到式（4）可以表达为

通过泰勒展开式得到

这里r＊界于r和r0之间，ℓn（r0）＝．

通过引理2，有ℓ′n（r0）＝op（1），这可以得到

注意到

ℓ″n（r＊）＝，这里．由于｜Xi－x0｜≤hn，当δ→0和n→∞，有max1≤i≤n｜ηi｜≤max1≤i≤n｜R（Xi）｜＋2δ→0．根据引理1，得到ℓ″n（r＊）＝θ－1fX（x0）Λ1（x0）S（1＋op（1））．设λ0为正定矩阵S的最小特征值．则对充分小的δ，有

这样结合式（19）和（20），得到式（18）．

通过式（18），ℓn（r）在的内部有一个局部最小值．在这个局部最小值，式（5）一定满足．设为最靠近r0的根．则＝1，这证明了定理1的结论．

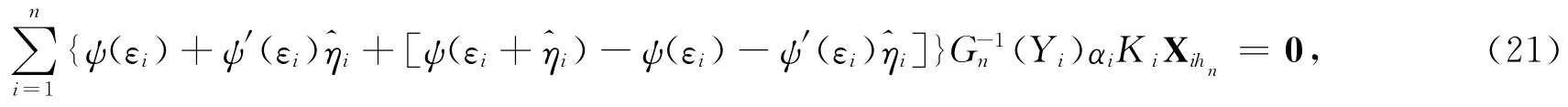
这里Xihn由定理1的证明中给出．注意到

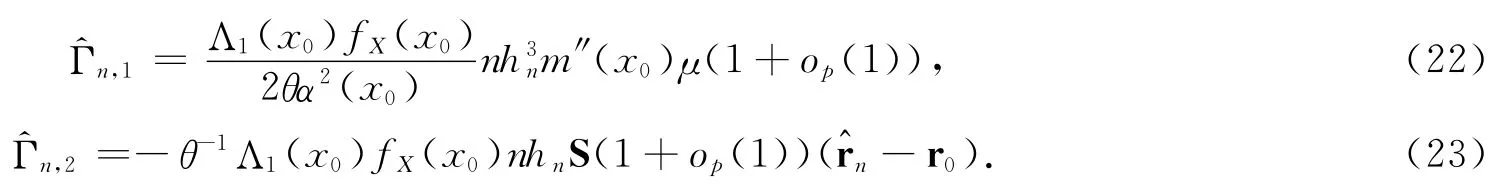
根据定理1的结果，得到

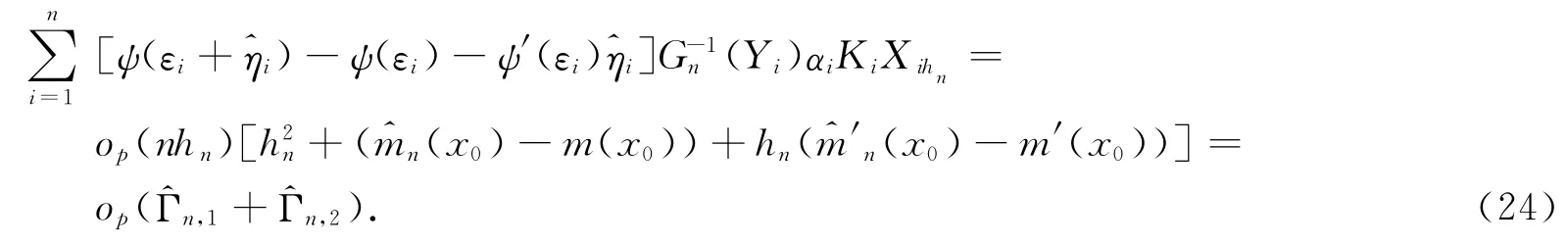
由式（21）～（24），得到

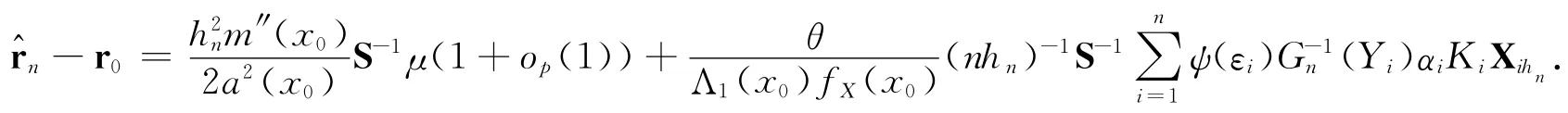
通过引理3，定理2得证．

［1］Fan Jianqiang，Jiang Jiancheng．Variable bandwidth and one－step local M－estimator［J］．Science in China Series A，2000，43（1）：65－81．

［2］Lynden－Bell D．A method of allowing for known observational selection in small samples applied to 3CR quasars［J］．Monthly Notices of the Royal Astronomical Society，1971，155：95－118．

［3］Ould－Saïd E，Lemdani M．Asymptotic properties of a nonparametric regression function estimator with randomly truncated data［J］．Ann Inst Statist Math，2006，58（2）：357－378．

［4］Jiang Jiancheng，Mack Y P．Robust local polynomial regression for dependent data［J］．Statistica Sinica，2001，11（3）：705－722．

［5］Cai Zongwu，Ould－Saïd E．Local M－estimator for nonparametric time series［J］．Statist Probab Lett，2003，65（4）：433－449．

［6］Woodroofe M．Estimating a distribution function with truncated data［J］．Ann Statist，1985，13（1）：163－177．