分担值与正规定则

张海侠

（许昌学院数学与统计学院，河南许昌461000）

1 引言及主要结果

1992年，Schwick首先发现了分担值与正规定则之间的联系，证明了下述结果：

定理1［1］设F为区域D内的一族亚纯函数，a1，a2，a3为3个互相判别的复数，若对任意f（z）∈F，f（z）与f′（z）在D内IM分担a1，a2，a3，则F在D内正规．

后来，庞学诚和Lawrence Zalcman改进了定理1，证明了以下的

定理2［2］设F为区域D内的一族亚纯函数，a，b为两个互相判别的复数，若对任意f（z）∈F，f（z）与f′（z）在D内IM分担a，b，则F在D内正规．

2005年，章文华得到下述结果：

定理3［3］设F为单位圆盘Δ上的一族亚纯函数，a是一个非零的有穷复数，若对任意f（z）∈F，f（z）与f′（z）在D内IM分担a，且f的零点是重级的，则F在D内正规．

后来，方明亮和L．Zalcman，叶亚盛和庞学诚得到了如下的

定理4［4］设F为单位圆盘Δ上的一族亚纯函数，a，b为任意两个非零有穷复数，k为正整数且若对于任意的f（z）∈F，f（z）的零点重级至少为k＋1，且f（z）＝a⇔f（k）（z）＝b，则F在Δ上正规．

笔者对上述定理作了一定的改进，得出以下结论，笔者将证明以下定理：

定理5 设F为单位圆盘Δ上的一族亚纯函数，a，b为任意两个非零有穷复数，k，l为正整数且k＞l．若对于任意的f（z）∈F，f（z）的零点重级至少为k＋1，极点重级至少为2且，则F在Δ上正规．

2 定义及主要引理

为便于叙述并讨论本文的主要结果，在此给出相关的定义及引理．

定义1 设F为复平面一区域D上的一组亚纯函数，如果F中任取一函数序列均可选出一子序列在区域D上按球距内闭一致收敛于一亚纯函数或，则称F在区域D上正规．

定义2 设f（z）和g（z）是区域D内的两个亚纯函数，a是一个复数，若f（z）－a与g（z）－a在D内有相同的零点，则称f（z）与g（z）在区域D内分担a，或称IM分担a．则记为f（z）＝a⇔g（z）＝a．

定义3 设f（z）和g（z）是区域D内的两个亚纯函数，a是一个复数，如果f（z）－a的零点为zn（n＝1，2，…），如果zn（n＝1，2，…）也是g（z）的零点（不计重数），或称单向分担a，则记为f（z）＝a⇒g（z）＝a．

引理1［5］（Zalcman引理）设F是单位圆盘Δ上的亚纯函数族，k∈N，F中任一函数f（z）的零点重级至少为k．设存在A≥1，使得对任意的，如果F在z0∈Δ处不正规，则对于任意的0≤α≤k，存在函数列｛fn（z）｝⊂F，点列zn→z0，正数列ρn→0，使得＝gn（ζ）→g（ζ）在复平面C上依球面距离内闭一致成立．其中g为C上的级不超过2的非常数亚纯函数，满足g＃（ζ）≤g＃（0）＝kA＋1．这里g＃（ζ）＝为球面导数．

引理2［6］设f（z）为复平面上的有穷级亚纯函数，b为非零复数，k为正整数．若f（z）的零点重级至少为k＋1，极点重级至少为2，且f（k）（z）≠b，则f（z）为一常数．

引理3［7］（Hurwitz定理）设函数序列在区域D内解析，并且在D内闭一致收敛到一个不恒为零的函数，γ是D内可求长的闭曲线，其内部属于D，且不经过f（z）的零点，则存在正整数N，使得当n≥N时，在γ内部，fn（z）和f（z）的零点个数是相同的．

3 定理5的证明

证明 假设F在z0∈Δ处不正规，则由引理1知，存在函数列fn（z）∈F，点列zn→z0，正数列ρn→0，使＝gn（ζ）→g（ζ）在复平面C的任意紧子集上依球面距离内闭一致成立，其中g（ζ）为C上的级不超过2的非常数亚纯函数，其零点重级至少为k＋1，极点重级至少为2．

可以断言：g（k）（ζ）≠a．

假设存在ζ0∈C使得g（k）（ζ0）＝a．

若g（k）（ζ）≡a，则g（ζ）为一个k次多项式，这与g（ζ）的零点重级至少为k＋1矛盾．因此，g（k）（ζ）不恒等于a．

根据Hurwitz's定理，存在gn（ζ）以及点列ζn→ζ0，使得当n充分大时，有＝a由

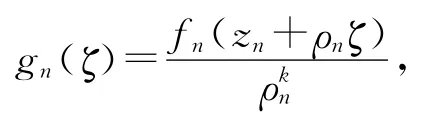
因此

［1］Schwick．W．Sharing values and normality［J］．Arch Math，1992，59：50－54．

［2］Pang Xuecheng，Zalcman L．Normal families and shared values［J］．Arkiv for Mathematics，2000，38（1）：171－182．

［3］章文华．分担值和正规族［J］．数学研究与评论，2005，25（2）：307－310．

［4］Fang Mingliang，Zaleman L．Normal families and shared values of meromorphic functions［J］．Annales Polonici Mathematici，2003，80：133－141．

［5］Pang Xuecheng，Zalcman L．Normal families and shared values［J］．Bull London Math Soc，2000，32（3）：325－331．

［6］Hayman W．K．Picard Value of Meromorphic Functions And Their Derivatives［J］．Annals of Mathematics，1959，70：9－42

［7］方企勤．复变函数教程［M］．北京：北京大学出版社，1996：234－256．