多模型块结构Laguerre函数预测控制在再热汽温系统中的应用
2013-03-23崔晓波陈雨亭秦文炜王致新吕剑虹
崔晓波 陈雨亭 秦文炜 王致新 吕剑虹
(东南大学能源与环境学院,南京 210096)
超临界机组再热汽温系统存在大惯性与大滞后等特点.大多数针对再热汽温系统控制方法的研究仅考虑了喷水调节[1-2];然而,实际的再热汽温系统是受挡板调节与喷水调节共同控制的,为了提高机组的经济性,喷水量应尽量小.在工程实际中,大部分再热汽温系统使用的是手动调节方式,而未投入自动调节方式;手动调节方式会使再热汽温喷水量大,且再热汽温经常超温.模型预测控制可以较好地解决大滞后问题[3-4],但传统的线性模型预测控制主要存在以下2个缺点[5]:① 用于非线性对象时控制性能较差;② 由于需要优化算法求解,导致计算量较大.
本文针对再热汽温系统的特点,提出了集成经济性的性能指标.为了克服传统模型预测控制的缺点,将Laguerre函数替代前移因子[6],有机融合块结构与多模型思想,提出了MMBLFPC控制方法.通过仿真研究与工程应用,证明了所提控制方法的有效性.
1 再热汽温调节原理
1.1 烟气挡板调节
锅炉尾部烟道包含2个并列的烟道.在烟温较低的省煤器下面布置可控制的烟气挡板,再热器烟道挡板和过热器烟道挡板配合动作,改变流经再热器烟道的烟气流量,从而控制再热蒸汽的温度(见图1).
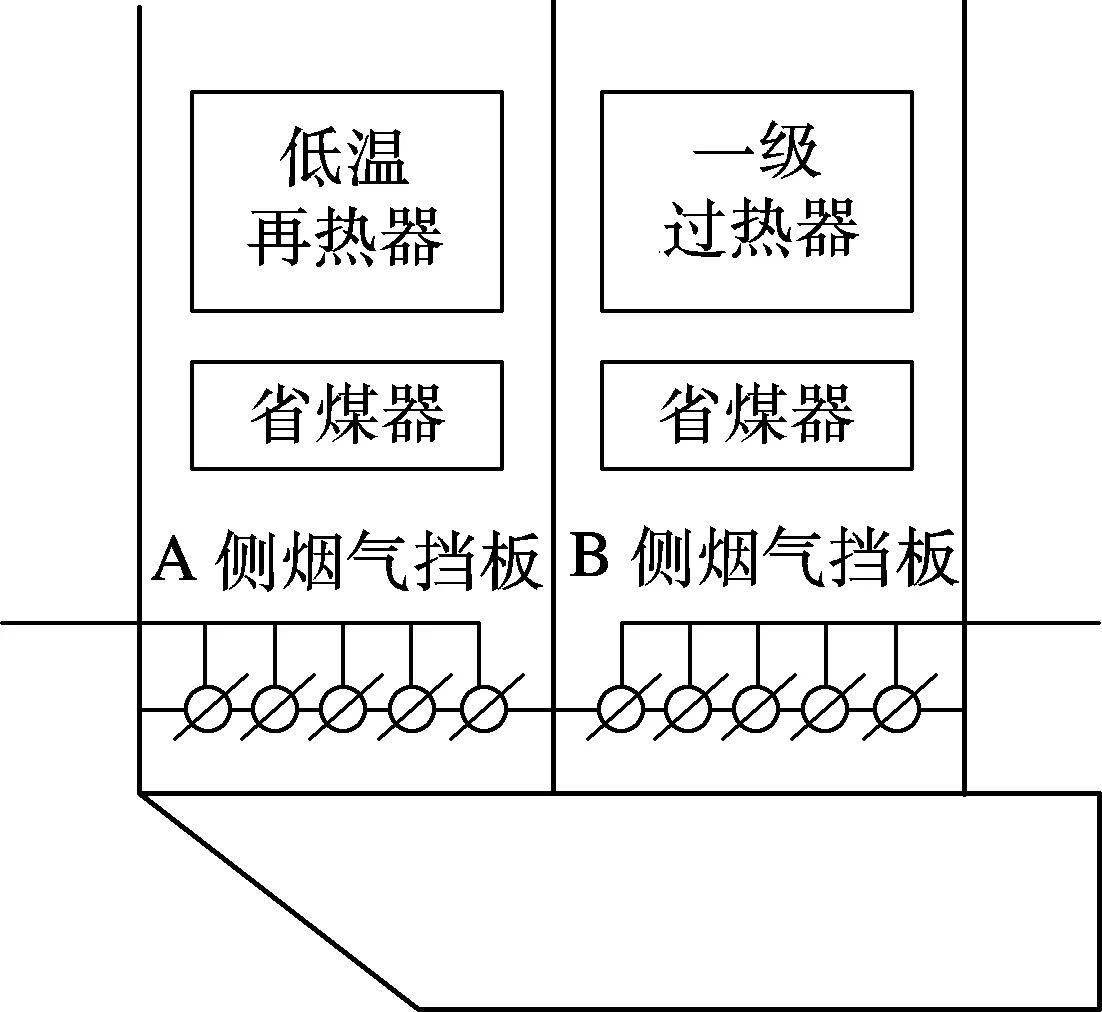
图1 挡板调节示意图
1.2 喷水减温调节
再热器喷水系统用于应对紧急事故进行喷水.由于挡板调温缓慢,事故喷水成为常规的再热汽温调节手段.喷水调节示意图见图2.
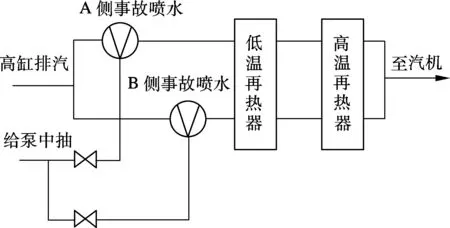
图2 喷水调节示意图
2 块结构预测控制
传统预测控制方法可表示为如下函数的极小化问题:
(1)
式中,J为性能指标函数值;Np为预测时域;Nc为控制时域;rk+i为k+i时刻的输出设定值;uk+i|k为k时刻时预测的k+i时刻的控制量;Δuk+i|k=uk+i|k-uk+i-1|k为k时刻时预测的k+i时刻的控制增量;yk+i|k为k时刻时预测的k+i时刻的被控量;Q与R为权重矩阵.
式(1)的极小化问题需满足如下约束条件:
xk=Axk-1+Buk-1
yk=Cxk
(2)
(3)
式中,xk-1,xk分别为k-1,k时刻的系统状态;uk-1为k-1时刻的控制量;yk为k时刻的被控量;umin,umax分别为控制量约束的上、下限;Δumin,Δumax分别为控制增量的上、下限;ymin,ymax分别为被控量的上、下限.
块结构预测控制是将常规的单步控制更改为多步控制,从而延长控制量的计算周期.
针对过热汽温系统的特性要求,性能指标中除了要考虑最小化再热汽温与设定值间的偏差外,还要考虑系统的经济性.再热器喷水量可以间接表征火电机组的循环效率,喷水量越少,机组的效率越高.同时,再热器喷水量又与喷水阀门开度相对应.因此,修改常规性能指标,得到如下的集成经济性的性能指标:
(4)
式中,Ru为经济性权重矩阵;QR为再热汽温偏差权重矩阵.在满足式(3)的前提下,通过最小化性能指标,得出控制量Δuk,Δuk+1,…,Δuk+Nc-1,并将其中的Δuk,Δuk+1,…,Δuk+M-1应用于被控对象,每隔M个采样时刻进行一次优化计算.
3 基于Laguerre函数的模型预测控制
3.1 离散Laguerre网络
离散Laguerre网络的表达式为
(5)
式中,a为待整定参数,且0≤a<1;z为后移因子;Γu(u=1,2,…,N)为u阶次的Laguerre网络系数.
本文选择Laguerre网络进行研究,是因为其具有较好的正交性[7].由式(5)可知
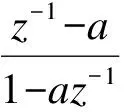
(6)
令l1(k)表示Γ1的逆Z变换,l2(k)表示Γ2的逆Z变换,以此类推,则离散Laguerre函数集合可以表示为如下的向量形式:
L(K)={l1(k),l2(k),…,lN(k)}T
(7)
由式(6)可得
L(K+1)=GL(K)
(8)
令β=1-a2,则矩阵G为N×N的方阵,且为a和β的函数.式(8)的初始条件可表示为

(9)
例如,当N=4时,有
(10)
3.2 模型预测控制
假设被控对象有p个输入、q个输出和n1个状态,则状态空间模型可表示为
xo(k+1)=Aoxo(k)+Bou(k)
y(k)=Coxo(k)
(11)
式中,u(k),y(k),xo(k)分别为k时刻原系统的控制量、被控量和状态量;Ao,Bo,Co为原系统的系数矩阵.
简单变化后,得到如下的增广状态空间模型:
(12)
式中,Δu(k),Δxo(k)分别为k时刻的控制增量和状态增量;Iq×q为q×q的单位矩阵.
将式(12)记为
x(k+1)=Ax(k)+BΔu(k)
y(k)=Cx(k)
(13)
则任意将来的控制增量可表示为
Δu(k+t)={Δu1(k+t),Δu2(k+t),…,Δup(k+t)}T
式中
Δui(k+t)=Li(t)Tηii=0,1,…,p
(14)
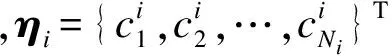

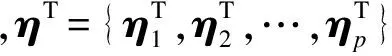
S(m)=AS(m-1)+S(1)(Gm-1)T
(16)
S(1)=BiLi(0)T
(17)
预测输出为
(18)
为了简化,将式(18)记为
y(k+m|k)=CAmx(k)+φ(m)Tη
(19)
式中,y(k+m|k)为k时刻时预测的k+m时刻的被控量值.
将式(19)代入式(4),将原来的“长”优化向量Δu转化为“短”优化向量η,则控制增量可表示为
(20)
利用式(20),可得出对应于式(3)的各约束表达式.对控制时域内的控制增量添加约束,可得到
M1η≤ΔUmax
-M1η≤-ΔUmin
(21)
式中,M1为控制增量的约束矩阵;ΔUmax,ΔUmin分别为控制增量的上限向量和下限向量.
考虑控制时域内所有控制量的约束可得
M2η≤Umax-u(k-1)
-M2η≤-Umin+u(k-1)
(22)
式中,M2为控制量的约束矩阵;Umax,Umin分别为控制量的上限向量和下限向量.
被控量的约束可表示为
ymin≤CAmx(k)+φ(m)Tη≤ymax
(23)
关于上述有约束的最优问题可以通过二次规划求解.
4 多模型预测控制
基于多个局部线性模型的多模型控制方法[8-10]是一种应用前景广阔的非线性控制技术.本文采用改进的递推贝叶斯加权方法,利用计算的权值对各子控制器进行加权求和,得到最终控制器的输出.权值计算公式为

(24)
式中,εj,k表示k时刻第j个子模型和被控对象输出
的相对误差,即绝对误差与初始输出量之比;K为递推计算的收敛系数,K越大,收敛到最真模型的速度越快;pj,k为k时刻第j个子模型和对象匹配程度的条件概率.
由式(24)可知,如果在某一时刻出现了子模型匹配概率为0的情况,那么该子模型将来的匹配概率也一直为0,故相应的子控制器在将来是不可用的.为了解决贝叶斯公式这一缺点,设定一个非常小的正实数δ,当pj,k≤δ时,使得pj,k=δ,以保证所有子控制器将来可用.则各子控制器的权值计算式为
(25)
将所得权值与各子控制器的输出量相乘,即可得到整个系统的实际控制作用为
(26)
5 仿真实验
通过对现场不同负荷下测试的实验数据进行拟合,得到如表1所示的再热汽温系统模型.

表1 再热汽温系统模型
不同工况点的稳态值见表2.所列数据为采用现场常规PID与前馈控制相结合的控制方法所得到的稳态数据.由表可知,在不同工况下喷水阀门均未关闭,存在一定的再热汽温喷水量,导致机组经济性较差.
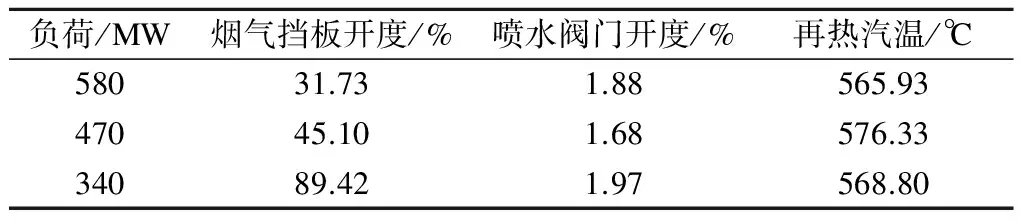
表2 不同工况下的稳态值
为了更好地进行比较,将MMBLFPC内部模型选择为如表3所示的降阶模型.其余参数选择如下:采样时间Ts=10 s,Np=70,Nc=30,M=3,QR=1/100,R=diag(0.08,0.01),Ru=diag(0,1),δ=0.01,K=500,a=0.6,N=6.传统的线性预测控制器内部模型选择为表3中负荷为470 MW的降阶模型,其余参数设置同上.每个控制量的约束均为[0,100],控制增量的约束均为[-10,10].
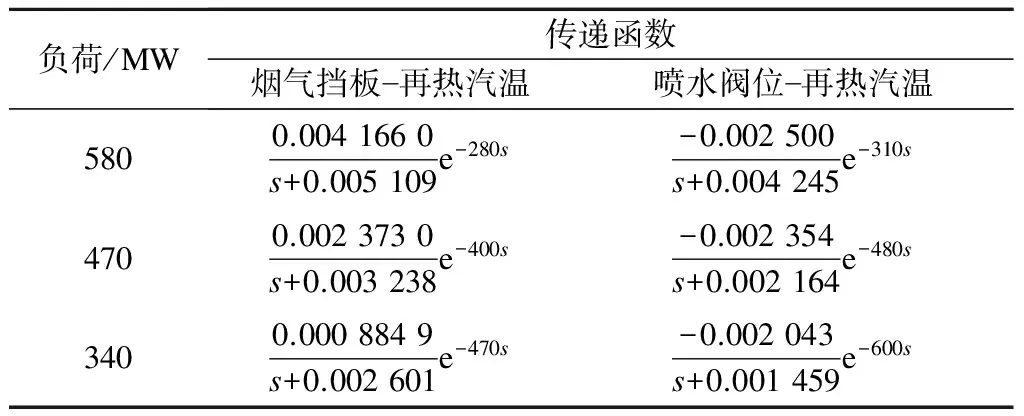
表3 控制器内部降阶模型
分别测试负荷Ne=580,340 MW时再热汽温的控制效果,结果见图3.由图可知,采用MMBLFPC控制方法后,再热汽温喷水阀门均最终关闭,减少了再热器喷水量,从而提高了经济性.在不同负荷工况下,仿真前半段设定值保持不变,采用MMBLFPC控制方法时喷水阀门快速关闭,同时为了保证再热汽温稳定,关小烟气挡板,再热汽温几乎不变;而采用线性预测控制方法时,超调量较大.从仿真后半段的设定值阶跃响应试验可以看出,采用MMBLFPC控制方法时响应迅速;而采用线性预测控制方法时,由于模型失配导致Ne=580 MW时系统振荡失稳,Ne=340 MW时调节缓慢.

图3 MMBLFPC与线性预测仿真比较
MMBLFPC控制方法是一种多模型控制策略,使用了3个内部模型,理论上其仿真时间是线性预测控制方法的3倍左右.然而,由图3可知,当Ne=580 MW时,采用MMBLFPC控制方法和线性预测控制方法的仿真时间分别为21.32和45.45 s;当Ne=340 MW时,两者的仿真时间则分别为30.79和89.61 s.究其原因在于,前者采用块结构预测控制,减少了优化计算次数,并结合Laguerre函数进行优化变量的数据压缩,从而进一步减少了仿真时间.
6 工程应用
以西门子S7-300 PLC为平台,MMBLFPC控制方法已正式应用于某电厂650 MW超临界机组上.再热汽温烟气挡板和事故喷水能长期稳定地投入运行,再热汽温具有良好的控制品质,取得了明显的经济效益.
6.1 定/变负荷下的汽温响应
再热汽温控制系统在定/变负荷下的汽温响应如图4所示.由图可知,在稳定负荷和变负荷的过程中,再热汽温均得到了有效控制,再热汽温的最大动态偏差仅为4 ℃.通过选择合适的权值QR与R,使再热汽温调节达到以烟气挡板调节为主、事故喷水为辅的方式进行控制,既保证汽温的小幅振荡,又达到短时事故喷水,有效地减少了喷水量,提高了机组的运行效率.
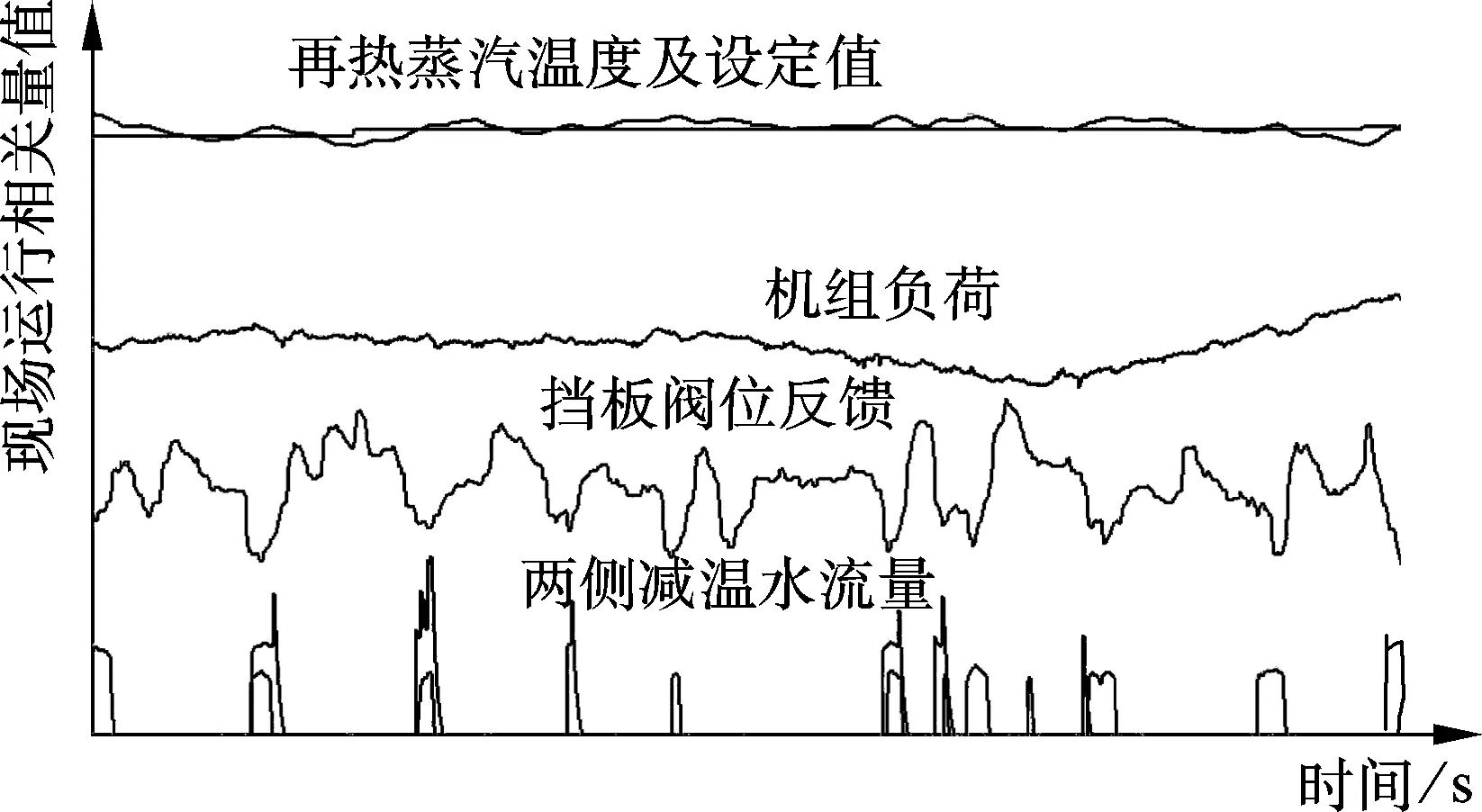
图4 定/变负荷下的汽温响应
6.2 新型系统控制性能分析
在控制系统投入运行及手动操作的情况下,再热汽温控制系统的动态响应如图5所示.图中记录了8 h的运行数据,其中,前4 h的运行数据表征的是控制系统投入运行后的系统响应,后4 h的运行数据表征的是手动操作情况下的系统响应.通过前后响应数据比较可知,在控制系统投入运行的情况下,再热汽温的最大动态偏差约为6 ℃;而在手动操作的情况下,再热汽温的最大动态偏差大于15 ℃,说明控制系统投入时的控制品质远优于人工操作的结果.此外,控制系统投入时,事故喷水阀打开的时间及总喷水量约为人工操作时的一半,从而有效提高了机组的运行效率.

图5 新型系统应用前后控制性能比较
7 结语
本文提出了一种基于Laguerre函数的块结构多模型预测控制技术.首先,采用块结构思想延长了控制量的计算周期,并引入了Laguerre函数进行控制量的数据压缩,以减少优化变量的个数,解决了传统预测控制优化计算量大的问题.然后,将此控制技术应用于再热汽温控制系统,提出了新的集成经济性优化的性能指标,解决了传统控制技术经济性差的缺点.最后,通过仿真实验与工程应用,证明了所提方法的有效性.
)
[1] 华志刚,吕剑虹,张铁军.状态变量-预测控制技术在600 MW机组再热汽温控制中的研究与应用[J].中国电机工程学报,2005,25(12):103-107.
Hua Zhigang,Lü Jianhong,Zhang Tiejun. Research and application of state variable-predictive control in 600 MW unit reheater temperature control system[J].ProceedingsoftheCSEE,2005,25(12): 103-107. (in Chinese)
[2] 岳俊红,刘吉臻,谭文,等. 改进的预测函数控制算法及其应用研究[J]. 中国电机工程学报,2007,27(11):93-97.
Yue Junhong,Liu Jizhen,Tan Wen,et al. Improved
predictive functional control algorithm and its application [J].ProceedingsoftheCSEE,2007,27(11): 93-97. (in Chinese)
[3] Maciejowski J M.Predictivecontrolwithconstraint[M]. London,UK: Prentice-Hall,2002: 103-106.
[4] Yang J,Li S,Chen X,et al. Disturbance rejection of dead-time processes using disturbance observer and model predictive control[J].ChemicalEngineeringResearchandDesign,2011,89(2): 125-135.
[5] Magni L,Raimondo D M,Allgöwer F.Nonlinearmodelpredictivecontroltowardsnewchallengingapplications[M]. Berlin,Germany: Springer,2009: 153-165.
[6] Wang L. Continuous time model predictive control design using orthonormal functions[J].InternationalJournalofControl,2001,74(16): 1588-1600.
[7] Masnadi-Shirazi M A,Aleshams M. Laguerre discrete-time filter design[J].Computers&ElectricalEngineering,2003,29(1): 173-192.
[8] Aufderheide B,Bequette B W. Extension of dynamic matrix control to multiple models[J].Computers&ChemicalEngineering,2003,27(8/9): 1079-1096.
[9] Kuure-Kinsey M,Bequette B W. Multiple model predictive control: a state estimation based approach[C]//Proceedingsof2007IEEEAmericanControlConference. New York,2007: 3739-3744.
[10] 于冲,吕剑虹,吴科.ALSTOM 气化炉的多模型预测控制[J]. 东南大学学报: 自然科学版,2010,40(4): 783-788.
Yu Chong,Lü Jianhong,Wu Ke. Multiple model predictive control for ALSTOM gasifier[J].JournalofSoutheastUniversity:NaturalScienceEdition,2010,40(4): 783-788. (in Chinese)
